2024华东师大版数学九年级下学期课时练--26.2.1 二次函数y=ax2的图象与性质(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--26.2.1 二次函数y=ax2的图象与性质(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 444.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 12:55:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
第26章 二次函数
26.2 二次函数的图象与性质
26.2.1 二次函数y=ax2的图象与性质
基础过关全练
知识点1 二次函数y=ax2(a≠0)的图象的画法
1.(2023海南海口中学期中)画函数y=x2的图象.
知识点2 二次函数y=ax2(a≠0)的图象与性质
2.(2023海南澄迈期末)关于抛物线y=-3x2,下列说法错误的是( )
A.图象关于直线x=0对称
B.抛物线开口向下
C.y随着x的增大而减小
D.图象的顶点为原点
3.(2022吉林白城通榆期末)当ab>0时,y=ax2与y=ax+b的图象大致是( )
A B C D
4.(2023安徽蚌埠五河模拟)二次函数①y=3x2;②y=x2;③y=x2的图象在同一坐标系中的开口大小顺序,从大到小排序应为( )
A.①>②>③ B.①>③>②
C.②>③>① D.②>①>③
5.【新考向·开放性试题】(2023湖南永州冷水滩期中)如果二次函数y=-(m-1)x2的图象开口向上,那么m的值可以是 .
6.(2023河南南阳卧龙期末)抛物线y=2x2在对称轴的左侧部分是
的(填“上升”或“下降”).
7.(2023山西临汾实验中学月考)抛物线y=4x2与直线y=kx+3的交点为(1,b),则k= .
8.(2023江苏扬州高邮模拟)已知二次函数y=x2,当-1≤x≤2时,函数值y的取值范围是 .
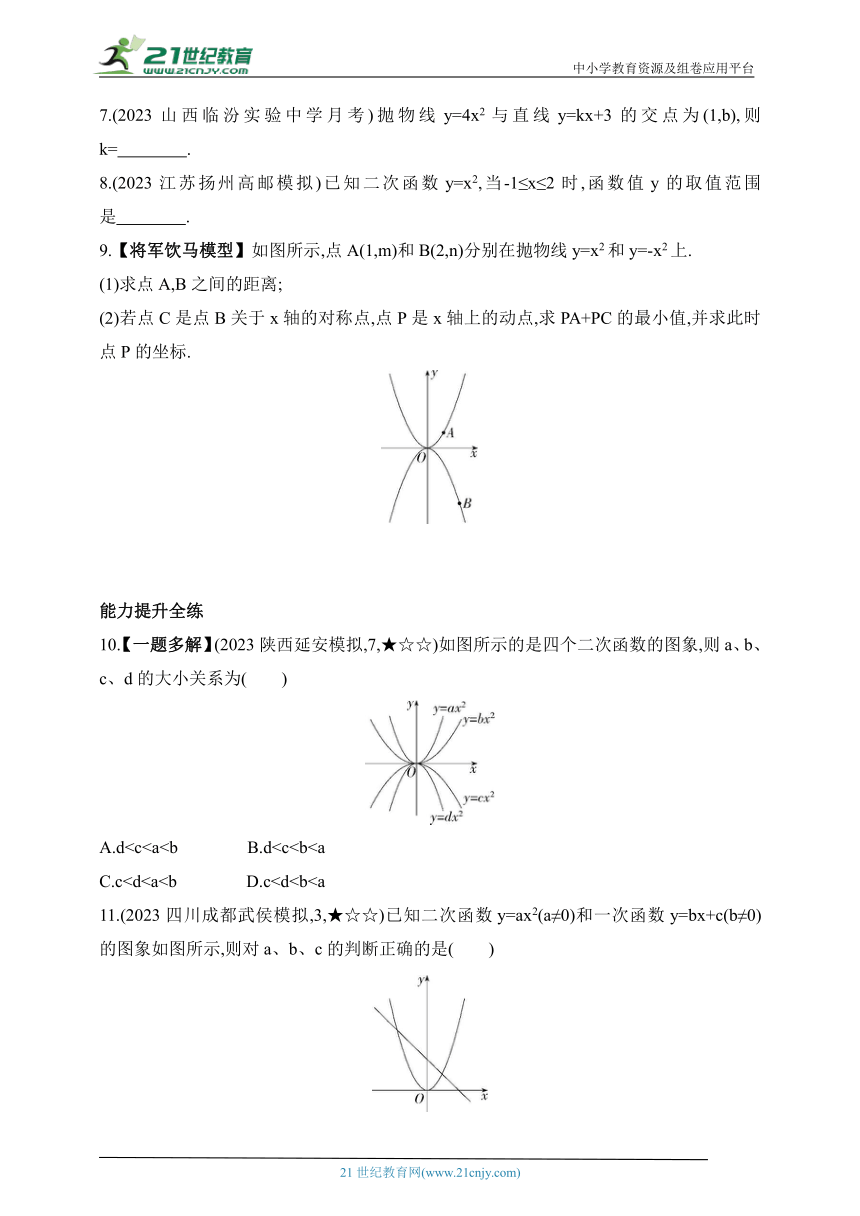
9.【将军饮马模型】如图所示,点A(1,m)和B(2,n)分别在抛物线y=x2和y=-x2上.
(1)求点A,B之间的距离;
(2)若点C是点B关于x轴的对称点,点P是x轴上的动点,求PA+PC的最小值,并求此时点P的坐标.
能力提升全练
10.【一题多解】(2023陕西延安模拟,7,★☆☆)如图所示的是四个二次函数的图象,则a、b、c、d的大小关系为( )
A.dC.c11.(2023四川成都武侯模拟,3,★☆☆)已知二次函数y=ax2(a≠0)和一次函数y=bx+c(b≠0)的图象如图所示,则对a、b、c的判断正确的是( )
A.a<0,b<0,c>0 B.a>0,b>0,c>0
C.a>0,b<0,c>0 D.a>0,b<0,c<0
12.(2023河南周口太康模拟,7,★★☆)已知点(x1,y1),(x2,y2)为二次函数y=-x2图象上的两点(不为顶点),则以下判断正确的是( )
A.若x1>x2,则y1>y2
B.若x1C.若x1x2<,则y1>y2
D.若x1x2>,则y113.(2023山东菏泽郓城模拟,8,★★☆)如图,在平面直角坐标系中,平行于x轴的直线y=2与二次函数y=x2,y=ax2分别交于A、B和C、D,若CD=2AB,则a的值为( )
A.4 B. C.2 D.
14.【新考法】(2023福建泉州晋江季延中学期末,16,★☆☆)对于二次函数y=ax2与y=bx2,其自变量与函数值的两组对应值如下表所示,根据二次函数图象的相关性质可知,m= ,d-c= .
x -1 m(m≠-1)
y=ax2 c c
y=bx2 c+3 d
15.【新考向·新定义试题】(2023四川成都武侯模拟,17,★★☆)定义:如果抛物线上关于对称轴对称的两点和抛物线的顶点构成的三角形是等边三角形,就称这个三角形为该抛物线的“完美三角形”.如图,△AOB是抛物线y=ax2的“完美三角形”,若△AOB的面积是4,则该抛物线的表达式为 .
16.(2023吉林长春绿园模拟,14,★★☆)如图,在平面直角坐标系中,四边形OABC是正方形,其边长为1,若点B为函数y=ax2(a<0)的图象上的点,∠1=15°,则a的值为 .
17.【新考向·代数推理】(2023江苏泰州兴化模拟,23,★☆☆)用代数推理的方法证明结论:已知二次函数y=x2,求证:当x>0时,y随x的增大而增大.
素养探究全练
18.【模型观念】(2023广东东莞中学模拟)孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线y=ax2(a<0)的性质时,将一块直角三角板的直角顶点置于平面直角坐标系的原点O处,两直角边与该抛物线交于A、B两点,请解答以下问题:
(1)如图1,若测得OA=OB=2,求a的值;
(2)对于同一条抛物线,孔明将三角板绕点O旋转到如图2所示的位置时,过B作BF⊥x轴于点F,测得OF=1,求此时点A、B的坐标;
(3)对该抛物线,孔明将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
答案全解全析
基础过关全练
1.解析 列表如下:
x … -3 -2 -1 0 1 2 3 …
y … 4.5 2 0.5 0 0.5 2 4.5 …
描点、连线得图象如下:
2.C ∵y=-3x2,∴抛物线开口向下,对称轴为y轴,顶点坐标是(0,0),∴A、B、D选项说法正确;∵a=-3<0,对称轴为y轴,∴当x>0时,y随x的增大而减小,∴C选项说法错误.
3.D 根据题意,ab>0,即a、b同号,当a>0,b>0时,y=ax2的图象开口向上,经过原点,y=ax+b的图象经过第一、二、三象限,此时,没有选项符合;当a<0,b<0时,y=ax2的图象开口向下,经过原点,y=ax+b的图象经过第二、三、四象限,此时D选项符合,故选D.
4.C ∵抛物线的开口大小是由二次项系数a的绝对值的大小确定的,|a|越大,则开口越小,∴开口大小从大到小排序应为②>③>①.
5.答案不唯一,如0
解析 由题意得-(m-1)>0,所以m<1,故m的值可以是0.
6.下降
解析 因为a=2>0,所以抛物线y=2x2在对称轴的左侧部分是下降的.
7.1
解析 把x=1代入抛物线y=4x2得y=4×1=4,即b=4,把(1,4)代入y=kx+3,得4=k+3,解得k=1.
8.0≤y≤4
解析 ∵抛物线的解析式为y=x2,∴该抛物线的对称轴为y轴,当x=0时,y=0,当x=-1时,y=(-1)2=1,当x=2时,y=22=4,∴0≤y≤4.
9.解析 (1)把A(1,m)代入y=x2得m=1,∴A(1,1).把(2,n)代入y=-x2得n=-4,∴B(2,-4),∴点A,B之间的距离AB==.
(2)∵点C是点B关于x轴的对称点,∴PC=PB,∴PA+PC=PA+PB,
∴当A,B,P三点共线时,PA+PB有最小值,即PA+PC有最小值,是线段AB的长,则PA+PC的最小值为.设直线AB的表达式为y=kx+b(k≠0),把(1,1)和(2,-4)代入得解得∴直线AB的表达式为y=-5x+6.把y=0代入y=-5x+6得-5x+6=0,解得x=,
∴此时点P的坐标为.
方法解读 如图,点A、B在直线l同侧,可作点B关于直线l的对称点B',连结AB'交直线l于点P,此时PA+PB的值最小.
能力提升全练
10.B (解法1:数形结合)如图,因为直线x=1与四条抛物线的交点从上到下依次为(1,a),(1,b),(1,c),(1,d),所以d(解法2:函数性质)由题中图象可知a,b均为正数,c,d均为负数.因为二次项系数的绝对值越大,抛物线开口越小,所以d11.C 由图象可知,二次函数y=ax2中,a>0,一次函数y=bx+c(b≠0)中,b<0,c>0.
12.D ∵y=-x2,a=-1<0,∴图象开口向下,对称轴为y轴,在y轴左侧,y随x的增大而增大,在y轴右侧,y随x的增大而减小,抛物线上的点离对称轴越远,函数值越小.
A.x1>x2时,y1不一定大于y2,例如x1=1时,y1=-1,x2=-1时,y2=-1,此时x1>x2,但是y1=y2,故错误;
B.x1C.x1x2<时,y1不一定大于y2,例如x1=-2时,y1=-4,x2=2时,y2=-4,此时x1x2<,但是y1=y2,故错误;
D.x1x2>时,即x1x2>x2x2>0,∴x1>x2>0或x1x2>0时,y113.B 将y=2代入y=x2得2=x2,解得x1=-,x2=,∴AB=2,∵CD=2AB,∴CD=4,∴D(2,2),将D(2,2)代入y=ax2得8a=2,解得a=.
14.1;3
解析 本题将求解的关键隐含在表格中,需要观察分析表格找到求解思路.由题表可知,x=-1和x=m时的函数值相等,∵题表中的两个函数对称轴都是直线x=0,∴m+(-1)=0,c+3=d,∴m=1,d-c=3.
15.y=x2
解析 ∵S△AOB=AB·AB·sin 60°=4,∴AB2=4,∴AB=4(负值已舍去),∴点B的坐标为(2,2).把(2,2)代入y=ax2得4a=2,解得a=,∴该抛物线的表达式为y=x2.
16.-
解析 如图,连结OB,作BD⊥y轴于D.∵四边形OABC是正方形,∴OB==.∵∠BOD=∠BOA+∠1=45°+15°=60°,∴BD=OB·sin∠BOD=OB·sin 60°=×=,OD=OB=,∴B,将B代入函数y=ax2(a<0),得-=a,∴a=-.
17.证明 设x1>x2>0,则y1=,y2=,∴y1-y2=-=(x1+x2)(x1-x2),∵x1>x2>0,∴(x1+x2)(x1-x2)>0,∴y1-y2>0,∴y1>y2,∴当x>0时,y随x的增大而增大.
素养探究全练
18.解析 (1)设线段AB与y轴的交点为C,由抛物线的对称性可得C为AB中点,∵OA=OB=2,∠AOB=90°,∴AC=OC=BC=2,∴B(2,-2),将B(2,-2)代入抛物线y=ax2(a<0)得-2=4a,解得a=-.
(2)如图,过点A作AE⊥x轴于点E,∵OF=1,BF⊥x轴,∴点B的横坐标为1,由(1)知y=-x2,∴B,∴BF=.∵∠AOB=90°,∴∠AOE+∠BOF=90°,∵∠BOF+
∠OBF=90°,∴∠AOE=∠OBF,∵∠AEO=∠OFB=90°,∴△AEO∽△OFB,
∴===2,∴AE=2OE,设点A(m>0),则OE=m,AE=m2,∴m2=2m,∴m=4,∴-m2=-8,∴点A的坐标为(-4,-8).
(3)设A(p>0),B,设直线AB的解析式为y=kx+b(k≠0),则①×n+②×p得(p+n)b=
-(p2n+pn2)=-pn(p+n),∴b=-pn,由(2)可得△AEO∽△OFB,∴=,∴=,∴pn=4,∴b=-×4=-2,∴无论k为何值,直线AB恒过点(0,-2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
第26章 二次函数
26.2 二次函数的图象与性质
26.2.1 二次函数y=ax2的图象与性质
基础过关全练
知识点1 二次函数y=ax2(a≠0)的图象的画法
1.(2023海南海口中学期中)画函数y=x2的图象.
知识点2 二次函数y=ax2(a≠0)的图象与性质
2.(2023海南澄迈期末)关于抛物线y=-3x2,下列说法错误的是( )
A.图象关于直线x=0对称
B.抛物线开口向下
C.y随着x的增大而减小
D.图象的顶点为原点
3.(2022吉林白城通榆期末)当ab>0时,y=ax2与y=ax+b的图象大致是( )
A B C D
4.(2023安徽蚌埠五河模拟)二次函数①y=3x2;②y=x2;③y=x2的图象在同一坐标系中的开口大小顺序,从大到小排序应为( )
A.①>②>③ B.①>③>②
C.②>③>① D.②>①>③
5.【新考向·开放性试题】(2023湖南永州冷水滩期中)如果二次函数y=-(m-1)x2的图象开口向上,那么m的值可以是 .
6.(2023河南南阳卧龙期末)抛物线y=2x2在对称轴的左侧部分是
的(填“上升”或“下降”).
7.(2023山西临汾实验中学月考)抛物线y=4x2与直线y=kx+3的交点为(1,b),则k= .
8.(2023江苏扬州高邮模拟)已知二次函数y=x2,当-1≤x≤2时,函数值y的取值范围是 .
9.【将军饮马模型】如图所示,点A(1,m)和B(2,n)分别在抛物线y=x2和y=-x2上.
(1)求点A,B之间的距离;
(2)若点C是点B关于x轴的对称点,点P是x轴上的动点,求PA+PC的最小值,并求此时点P的坐标.
能力提升全练
10.【一题多解】(2023陕西延安模拟,7,★☆☆)如图所示的是四个二次函数的图象,则a、b、c、d的大小关系为( )
A.d
A.a<0,b<0,c>0 B.a>0,b>0,c>0
C.a>0,b<0,c>0 D.a>0,b<0,c<0
12.(2023河南周口太康模拟,7,★★☆)已知点(x1,y1),(x2,y2)为二次函数y=-x2图象上的两点(不为顶点),则以下判断正确的是( )
A.若x1>x2,则y1>y2
B.若x1
D.若x1x2>,则y1
A.4 B. C.2 D.
14.【新考法】(2023福建泉州晋江季延中学期末,16,★☆☆)对于二次函数y=ax2与y=bx2,其自变量与函数值的两组对应值如下表所示,根据二次函数图象的相关性质可知,m= ,d-c= .
x -1 m(m≠-1)
y=ax2 c c
y=bx2 c+3 d
15.【新考向·新定义试题】(2023四川成都武侯模拟,17,★★☆)定义:如果抛物线上关于对称轴对称的两点和抛物线的顶点构成的三角形是等边三角形,就称这个三角形为该抛物线的“完美三角形”.如图,△AOB是抛物线y=ax2的“完美三角形”,若△AOB的面积是4,则该抛物线的表达式为 .
16.(2023吉林长春绿园模拟,14,★★☆)如图,在平面直角坐标系中,四边形OABC是正方形,其边长为1,若点B为函数y=ax2(a<0)的图象上的点,∠1=15°,则a的值为 .
17.【新考向·代数推理】(2023江苏泰州兴化模拟,23,★☆☆)用代数推理的方法证明结论:已知二次函数y=x2,求证:当x>0时,y随x的增大而增大.
素养探究全练
18.【模型观念】(2023广东东莞中学模拟)孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线y=ax2(a<0)的性质时,将一块直角三角板的直角顶点置于平面直角坐标系的原点O处,两直角边与该抛物线交于A、B两点,请解答以下问题:
(1)如图1,若测得OA=OB=2,求a的值;
(2)对于同一条抛物线,孔明将三角板绕点O旋转到如图2所示的位置时,过B作BF⊥x轴于点F,测得OF=1,求此时点A、B的坐标;
(3)对该抛物线,孔明将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
答案全解全析
基础过关全练
1.解析 列表如下:
x … -3 -2 -1 0 1 2 3 …
y … 4.5 2 0.5 0 0.5 2 4.5 …
描点、连线得图象如下:
2.C ∵y=-3x2,∴抛物线开口向下,对称轴为y轴,顶点坐标是(0,0),∴A、B、D选项说法正确;∵a=-3<0,对称轴为y轴,∴当x>0时,y随x的增大而减小,∴C选项说法错误.
3.D 根据题意,ab>0,即a、b同号,当a>0,b>0时,y=ax2的图象开口向上,经过原点,y=ax+b的图象经过第一、二、三象限,此时,没有选项符合;当a<0,b<0时,y=ax2的图象开口向下,经过原点,y=ax+b的图象经过第二、三、四象限,此时D选项符合,故选D.
4.C ∵抛物线的开口大小是由二次项系数a的绝对值的大小确定的,|a|越大,则开口越小,∴开口大小从大到小排序应为②>③>①.
5.答案不唯一,如0
解析 由题意得-(m-1)>0,所以m<1,故m的值可以是0.
6.下降
解析 因为a=2>0,所以抛物线y=2x2在对称轴的左侧部分是下降的.
7.1
解析 把x=1代入抛物线y=4x2得y=4×1=4,即b=4,把(1,4)代入y=kx+3,得4=k+3,解得k=1.
8.0≤y≤4
解析 ∵抛物线的解析式为y=x2,∴该抛物线的对称轴为y轴,当x=0时,y=0,当x=-1时,y=(-1)2=1,当x=2时,y=22=4,∴0≤y≤4.
9.解析 (1)把A(1,m)代入y=x2得m=1,∴A(1,1).把(2,n)代入y=-x2得n=-4,∴B(2,-4),∴点A,B之间的距离AB==.
(2)∵点C是点B关于x轴的对称点,∴PC=PB,∴PA+PC=PA+PB,
∴当A,B,P三点共线时,PA+PB有最小值,即PA+PC有最小值,是线段AB的长,则PA+PC的最小值为.设直线AB的表达式为y=kx+b(k≠0),把(1,1)和(2,-4)代入得解得∴直线AB的表达式为y=-5x+6.把y=0代入y=-5x+6得-5x+6=0,解得x=,
∴此时点P的坐标为.
方法解读 如图,点A、B在直线l同侧,可作点B关于直线l的对称点B',连结AB'交直线l于点P,此时PA+PB的值最小.
能力提升全练
10.B (解法1:数形结合)如图,因为直线x=1与四条抛物线的交点从上到下依次为(1,a),(1,b),(1,c),(1,d),所以d
12.D ∵y=-x2,a=-1<0,∴图象开口向下,对称轴为y轴,在y轴左侧,y随x的增大而增大,在y轴右侧,y随x的增大而减小,抛物线上的点离对称轴越远,函数值越小.
A.x1>x2时,y1不一定大于y2,例如x1=1时,y1=-1,x2=-1时,y2=-1,此时x1>x2,但是y1=y2,故错误;
B.x1
D.x1x2>时,即x1x2>x2x2>0,∴x1>x2>0或x1
14.1;3
解析 本题将求解的关键隐含在表格中,需要观察分析表格找到求解思路.由题表可知,x=-1和x=m时的函数值相等,∵题表中的两个函数对称轴都是直线x=0,∴m+(-1)=0,c+3=d,∴m=1,d-c=3.
15.y=x2
解析 ∵S△AOB=AB·AB·sin 60°=4,∴AB2=4,∴AB=4(负值已舍去),∴点B的坐标为(2,2).把(2,2)代入y=ax2得4a=2,解得a=,∴该抛物线的表达式为y=x2.
16.-
解析 如图,连结OB,作BD⊥y轴于D.∵四边形OABC是正方形,∴OB==.∵∠BOD=∠BOA+∠1=45°+15°=60°,∴BD=OB·sin∠BOD=OB·sin 60°=×=,OD=OB=,∴B,将B代入函数y=ax2(a<0),得-=a,∴a=-.
17.证明 设x1>x2>0,则y1=,y2=,∴y1-y2=-=(x1+x2)(x1-x2),∵x1>x2>0,∴(x1+x2)(x1-x2)>0,∴y1-y2>0,∴y1>y2,∴当x>0时,y随x的增大而增大.
素养探究全练
18.解析 (1)设线段AB与y轴的交点为C,由抛物线的对称性可得C为AB中点,∵OA=OB=2,∠AOB=90°,∴AC=OC=BC=2,∴B(2,-2),将B(2,-2)代入抛物线y=ax2(a<0)得-2=4a,解得a=-.
(2)如图,过点A作AE⊥x轴于点E,∵OF=1,BF⊥x轴,∴点B的横坐标为1,由(1)知y=-x2,∴B,∴BF=.∵∠AOB=90°,∴∠AOE+∠BOF=90°,∵∠BOF+
∠OBF=90°,∴∠AOE=∠OBF,∵∠AEO=∠OFB=90°,∴△AEO∽△OFB,
∴===2,∴AE=2OE,设点A(m>0),则OE=m,AE=m2,∴m2=2m,∴m=4,∴-m2=-8,∴点A的坐标为(-4,-8).
(3)设A(p>0),B,设直线AB的解析式为y=kx+b(k≠0),则①×n+②×p得(p+n)b=
-(p2n+pn2)=-pn(p+n),∴b=-pn,由(2)可得△AEO∽△OFB,∴=,∴=,∴pn=4,∴b=-×4=-2,∴无论k为何值,直线AB恒过点(0,-2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
