2024华东师大版数学九年级下学期课时练--26.2.3 求二次函数的表达式(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--26.2.3 求二次函数的表达式(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 445.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 13:46:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
第26章 二次函数
26.2 二次函数的图象与性质
26.2.3 求二次函数的表达式
基础过关全练
知识点 求二次函数的表达式
1.(2023福建漳州华安期末)一抛物线的形状、开口方向与抛物线y=x2-2x+3相同,顶点坐标为(-2,1),则此抛物线的解析式为( )
A.y=(x-2)2+1 B.y=(x+2)2-1
C.y=(x+2)2+1 D.y=(x-2)2-1
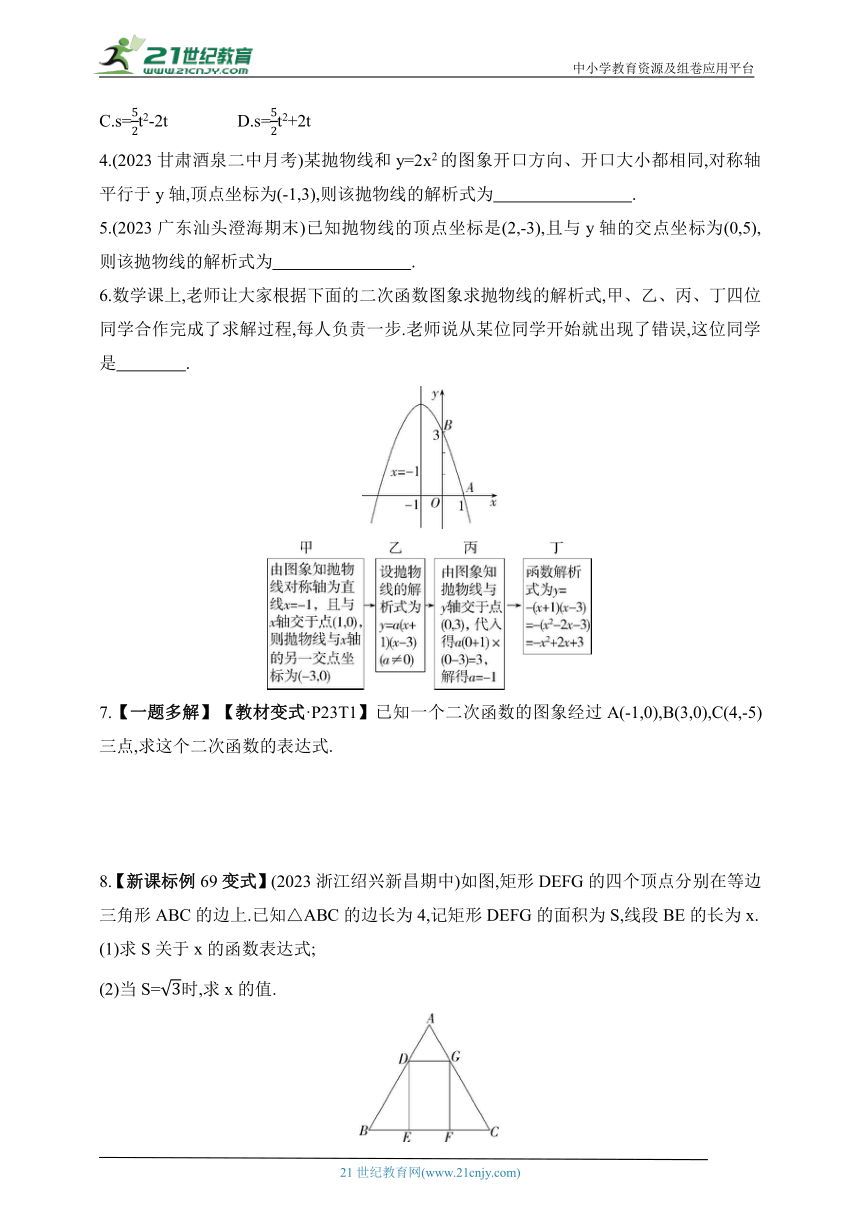
2.(2023四川眉山洪雅期中)如图,函数的解析式为( )
A.y=x2- B.y=4-x2
C.y=-x2+3 D.y=(3-x2)
3.【跨学科·体育与健康】(2023福建泉州五中期中)滑雪爱好者小张从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据如下(如表),为观察s与t之间的关系,建立坐标系(如图),以t为横坐标,s为纵坐标绘制了如图所示的函数图象.
滑行时间t/s 0 1 2 3 4
滑行距离s/m 0 4.5 14 28.5 48
根据以上信息,可知s与t的函数关系式是(不考虑取值范围)( )
A.s=t2+3t B.s=t2-3t
C.s=t2-2t D.s=t2+2t
4.(2023甘肃酒泉二中月考)某抛物线和y=2x2的图象开口方向、开口大小都相同,对称轴平行于y轴,顶点坐标为(-1,3),则该抛物线的解析式为 .
5.(2023广东汕头澄海期末)已知抛物线的顶点坐标是(2,-3),且与y轴的交点坐标为(0,5),则该抛物线的解析式为 .
6.数学课上,老师让大家根据下面的二次函数图象求抛物线的解析式,甲、乙、丙、丁四位同学合作完成了求解过程,每人负责一步.老师说从某位同学开始就出现了错误,这位同学是 .
7.【一题多解】【教材变式·P23T1】已知一个二次函数的图象经过A(-1,0),B(3,0),C(4,-5)三点,求这个二次函数的表达式.
8.【新课标例69变式】(2023浙江绍兴新昌期中)如图,矩形DEFG的四个顶点分别在等边三角形ABC的边上.已知△ABC的边长为4,记矩形DEFG的面积为S,线段BE的长为x.
(1)求S关于x的函数表达式;
(2)当S=时,求x的值.
能力提升全练
9.(2023湖南永州冷水滩模拟,8,★★☆)在平面直角坐标系中,抛物线y=x2-4x+5与y轴交于点C,则该抛物线关于点C成中心对称的抛物线的表达式为( )
A.y=-x2-4x+5 B.y=x2+4x+5
C.y=-x2+4x-5 D.y=-x2-4x-5
10.【新考法】(2023河南开封兰考模拟,10,★★☆)在“探索函数y=ax2+bx+c的系数a,b,c与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中a的值最大为( )
A. B. C. D.
11.【新考向·开放性试题】(2023上海中考,14,★☆☆)一个二次函数y=ax2+bx+c的图象的顶点在y轴正半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的解析式可以是 .
12.(2021河南南阳模拟,21,★★☆)如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
13.【分类讨论思想】(2022河南三门峡一模,22,★★☆)已知二次函数y=ax2-2ax+2a(a≠0).
(1)该二次函数图象的对称轴是直线x= ;
(2)若该二次函数的图象开口向上,当-1≤x≤4时,y的最大值是5,求抛物线的解析式;
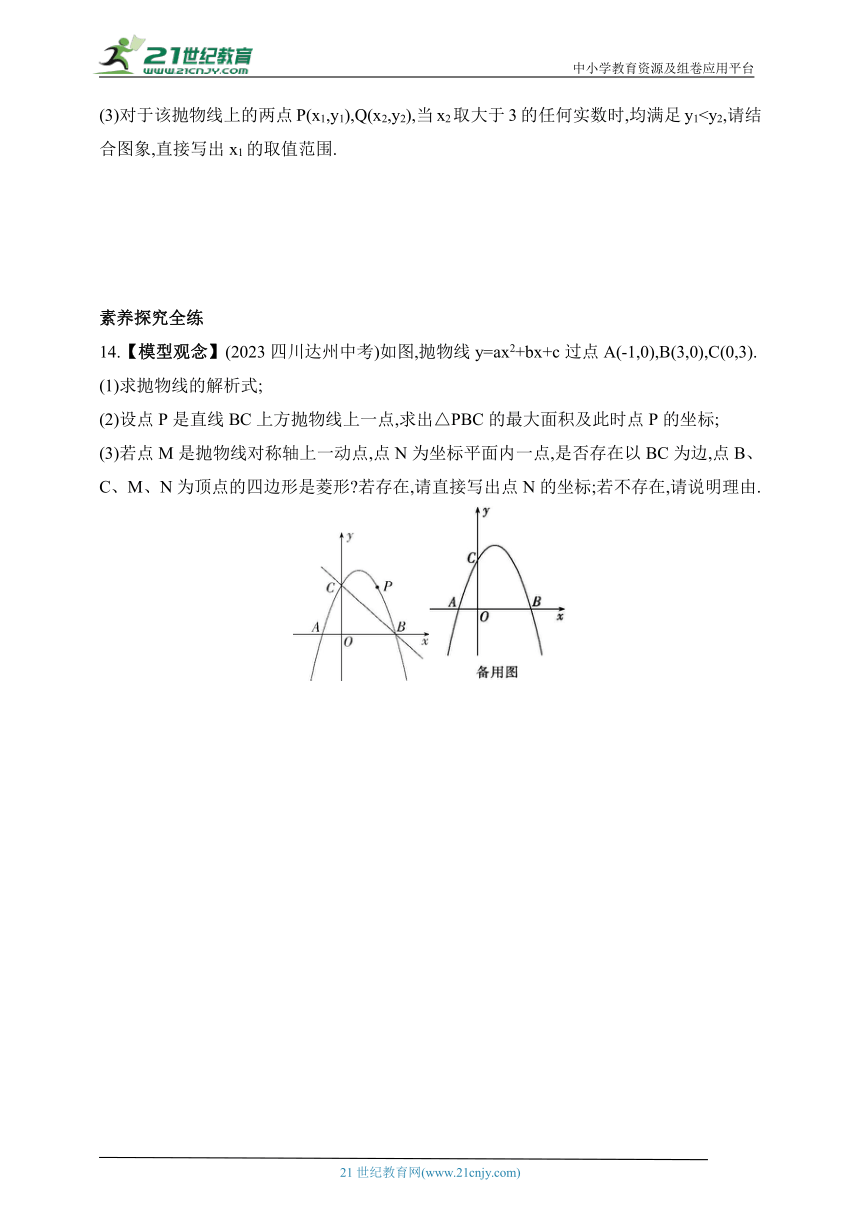
(3)对于该抛物线上的两点P(x1,y1),Q(x2,y2),当x2取大于3的任何实数时,均满足y1素养探究全练
14.【模型观念】(2023四川达州中考)如图,抛物线y=ax2+bx+c过点A(-1,0),B(3,0),C(0,3).
(1)求抛物线的解析式;
(2)设点P是直线BC上方抛物线上一点,求出△PBC的最大面积及此时点P的坐标;
(3)若点M是抛物线对称轴上一动点,点N为坐标平面内一点,是否存在以BC为边,点B、C、M、N为顶点的四边形是菱形 若存在,请直接写出点N的坐标;若不存在,请说明理由.
答案全解全析
基础过关全练
C ∵抛物线的形状、开口方向与抛物线y=x2-2x+3相同,∴a=,
∵顶点坐标为(-2,1),∴此抛物线的解析式为y=(x+2)2+1.
2.C 由图象可知抛物线与x轴的交点坐标为(-2,0),(2,0),故设抛物线解析式为y=a(x+2)(x-2)(a≠0).由图象知抛物线经过点(0,3),将(0,3)代入得a(0+2)×(0-2)=3,解得a=-,∴抛物线解析式为y=-(x+2)(x-2)=-x2+3.
3.D 观察函数图象可知s与t为二次函数关系,设s=at2+bt+c(a≠0),将(0,0),(1,4.5),(2,14)代入s=at2+bt+c得解得∴s与t的函数关系式是s=t2+2t.
4.y=2x2+4x+5
解析 已知该抛物线的顶点坐标为(-1,3),可设此抛物线的解析式为y=a(x+1)2+3(a≠0),由于该抛物线和y=2x2的图象开口方向、开口大小都相同,因此a=2,故该抛物线的解析式为y=2(x+1)2+3=2x2+4x+5.
5.y=2x2-8x+5
解析 由题意设该抛物线的解析式为y=a(x-2)2-3(a≠0),将(0,5)代入得5=a(0-2)2-3,解得a=2,∴y=2(x-2)2-3=2x2-8x+5.
6.乙
解析 从乙同学开始出现错误.根据题图可设抛物线的解析式为y=a(x-1)(x+3)(a≠0),由图象知抛物线与y轴交于点(0,3),代入得a(0-1)×(0+3)=3,解得a=-1,∴函数解析式为y=-(x-1)(x+3)=-(x2+2x-3)=-x2-2x+3.
7.解析 (解法1:设一般式)设所求二次函数的表达式为y=ax2+bx+c(a≠0),把A(-1,0),B(3,0),C(4,-5)代入得解得
∴二次函数的表达式为y=-x2+2x+3.
(解法2:设交点式)∵二次函数的图象与x轴的两个交点分别为
A(-1,0),B(3,0),∴可设这个二次函数的表达式为y=a(x+1)(x-3)(a≠0).
∵图象经过点C(4,-5),∴-5=a×5×1,解得a=-1,∴二次函数的表达式为y=-(x+1)(x-3),即y=-x2+2x+3.
(解法3:设顶点式)∵二次函数的图象与x轴的两个交点分别为A
(-1,0),B(3,0),∴这个二次函数的图象的对称轴为直线x=1,设所求抛物线的函数表达式为y=a(x-1)2+k(a≠0),把A(-1,0),C(4,-5)代入得解得∴二次函数的表达式为y=-(x-1)2+4,即y=-x2+2x+3.
8.解析 (1)∵△ABC是等边三角形,∴∠B=60°,∵矩形DEFG的四个顶点分别在等边三角形ABC的边上,∴∠BED=90°,BE=CF=x,
∴EF=4-2x,∴DE=BE·tan 60°=x,∴S=DE·EF=x·(4-2x)=
-2x2+4x(0(2)∵S=,∴-2x2+4x=,∴2x2-4x+1=0,解得x=1±.∵0能力提升全练
9.A 由抛物线y=x2-4x+5=(x-2)2+1知抛物线顶点坐标是(2,1),a=1,由抛物线y=x2-4x+5知C(0,5),∴该抛物线关于点C成中心对称的抛物线的顶点坐标是(-2,9),a=-1,∴该抛物线关于点C成中心对称的抛物线的表达式为y=-(x+2)2+9=-x2-4x+5.
10.A 本题借助二次函数的大致图象确定解析式中二次项系数的值,设计新颖别致.由题图知,A、B、D三点组成的二次函数图象开口向上,a>0;A、B、C三点组成的二次函数图象开口向上,a>0;B、C、D三点组成的二次函数图象开口向下,a<0;A、D、C三点组成的二次函数图象开口向下,a<0,即只需比较A、B、D三点组成的抛物线和A、B、C三点组成的抛物线即可.设A、B、C三点组成的抛物线解析式为y=a1x2+b1x+c1(a1≠0),把A(0,2),B(1,0),C(3,1)代入得解得a1=.设A、B、D三点组成的抛物线解析式为y=ax2+bx+c(a≠0),把A(0,2),B(1,0),D(2,3)代入得解得a=,∵<,∴a的最大值为.
11.答案不唯一,如y=-x2+1
解析 由题意得b=0,a<0,c>0,∴这个二次函数的解析式可以是y=
-x2+1.(答案不唯一)
12.解析 (1)把A(-1,0)、B(3,0)代入y=x2+bx+c得解得∴抛物线的解析式为y=x2-2x-3,∵y=x2-2x-3=(x-1)2-4,∴顶点坐标为(1,-4).
(2)∵A(-1,0)、B(3,0),∴AB=3-(-1)=4,设P点坐标为(t,t2-2t-3),∵S△PAB=10,∴×4×|t2-2t-3|=10,∴t2-2t-3=±5,当t2-2t-3=5时,解得t1=
-2,t2=4,此时P点坐标为(-2,5)或(4,5);当t2-2t-3=-5时,方程没有实数解,故P点坐标为(-2,5)或(4,5).
13.解析 (1)对称轴为直线x=-=1.
(2)∵该二次函数的图象开口向上,对称轴为直线x=1,且当-1≤x≤4时,y的最大值是5,∴当x=4时,y=5,∴代入得,16a-8a+2a=5,∴a=,∴抛物线的解析式为y=x2-x+1.
(3)∵对称轴为直线x=1,∴x=-1与x=3时的y值相等,∵x2>3时,均满足y1①当a<0时,抛物线开口向下,如图1,不成立;
②当a>0时,抛物线开口向上,如图2,当x2取大于3的任何实数时,均满足y1图1
图2
综上所述,当x2取大于3的任何实数时,均满足y1素养探究全练
14.解析 (1)由题意得,抛物线的表达式为y=a(x+1)×(x-3)=a(x2-2x-3),将C(0,3)代入得-3a=3,解得a=-1,故抛物线的表达式为y=-x2+2x+3.
(2)由点B、C的坐标得直线BC的表达式为y=-x+3,如图,过点P作y轴的平行线交CB于点H,连结PC,PB,设点P(x,-x2+2x+3),则点H(x,
-x+3),∴△PBC的面积=S△PHC+S△PHB=PH·OB=(-x2+3x)=
-+,∵a=-<0,∴当x=时△PBC的面积有最大值,为,此时点P.
(3)存在.理由:由(1)知抛物线的解析式为y=-x2+2x+3,∴对称轴为直线x=1,设点M(1,t),N(x,y),分情况求解如下:
①若BC为菱形BCMN的边,则BC2=CM2,即18=12+(t-3)2,解得t1=+3,t2=-+3,∵∴x=4,y=t-3,∴N1(4,),N2(4,
-).
②若BC为菱形BCNM的边,则BC2=BM2,即18=(3-1)2+t2,解得t3=,t4=-,
∵∴x=-2,y=3+t,
∴N3(-2,+3),N4(-2,-+3).
综上所述,点N的坐标为(4,-)或(4,)或(-2,+3)或(-2,-+3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
第26章 二次函数
26.2 二次函数的图象与性质
26.2.3 求二次函数的表达式
基础过关全练
知识点 求二次函数的表达式
1.(2023福建漳州华安期末)一抛物线的形状、开口方向与抛物线y=x2-2x+3相同,顶点坐标为(-2,1),则此抛物线的解析式为( )
A.y=(x-2)2+1 B.y=(x+2)2-1
C.y=(x+2)2+1 D.y=(x-2)2-1
2.(2023四川眉山洪雅期中)如图,函数的解析式为( )
A.y=x2- B.y=4-x2
C.y=-x2+3 D.y=(3-x2)
3.【跨学科·体育与健康】(2023福建泉州五中期中)滑雪爱好者小张从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据如下(如表),为观察s与t之间的关系,建立坐标系(如图),以t为横坐标,s为纵坐标绘制了如图所示的函数图象.
滑行时间t/s 0 1 2 3 4
滑行距离s/m 0 4.5 14 28.5 48
根据以上信息,可知s与t的函数关系式是(不考虑取值范围)( )
A.s=t2+3t B.s=t2-3t
C.s=t2-2t D.s=t2+2t
4.(2023甘肃酒泉二中月考)某抛物线和y=2x2的图象开口方向、开口大小都相同,对称轴平行于y轴,顶点坐标为(-1,3),则该抛物线的解析式为 .
5.(2023广东汕头澄海期末)已知抛物线的顶点坐标是(2,-3),且与y轴的交点坐标为(0,5),则该抛物线的解析式为 .
6.数学课上,老师让大家根据下面的二次函数图象求抛物线的解析式,甲、乙、丙、丁四位同学合作完成了求解过程,每人负责一步.老师说从某位同学开始就出现了错误,这位同学是 .
7.【一题多解】【教材变式·P23T1】已知一个二次函数的图象经过A(-1,0),B(3,0),C(4,-5)三点,求这个二次函数的表达式.
8.【新课标例69变式】(2023浙江绍兴新昌期中)如图,矩形DEFG的四个顶点分别在等边三角形ABC的边上.已知△ABC的边长为4,记矩形DEFG的面积为S,线段BE的长为x.
(1)求S关于x的函数表达式;
(2)当S=时,求x的值.
能力提升全练
9.(2023湖南永州冷水滩模拟,8,★★☆)在平面直角坐标系中,抛物线y=x2-4x+5与y轴交于点C,则该抛物线关于点C成中心对称的抛物线的表达式为( )
A.y=-x2-4x+5 B.y=x2+4x+5
C.y=-x2+4x-5 D.y=-x2-4x-5
10.【新考法】(2023河南开封兰考模拟,10,★★☆)在“探索函数y=ax2+bx+c的系数a,b,c与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中a的值最大为( )
A. B. C. D.
11.【新考向·开放性试题】(2023上海中考,14,★☆☆)一个二次函数y=ax2+bx+c的图象的顶点在y轴正半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的解析式可以是 .
12.(2021河南南阳模拟,21,★★☆)如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
13.【分类讨论思想】(2022河南三门峡一模,22,★★☆)已知二次函数y=ax2-2ax+2a(a≠0).
(1)该二次函数图象的对称轴是直线x= ;
(2)若该二次函数的图象开口向上,当-1≤x≤4时,y的最大值是5,求抛物线的解析式;
(3)对于该抛物线上的两点P(x1,y1),Q(x2,y2),当x2取大于3的任何实数时,均满足y1
14.【模型观念】(2023四川达州中考)如图,抛物线y=ax2+bx+c过点A(-1,0),B(3,0),C(0,3).
(1)求抛物线的解析式;
(2)设点P是直线BC上方抛物线上一点,求出△PBC的最大面积及此时点P的坐标;
(3)若点M是抛物线对称轴上一动点,点N为坐标平面内一点,是否存在以BC为边,点B、C、M、N为顶点的四边形是菱形 若存在,请直接写出点N的坐标;若不存在,请说明理由.
答案全解全析
基础过关全练
C ∵抛物线的形状、开口方向与抛物线y=x2-2x+3相同,∴a=,
∵顶点坐标为(-2,1),∴此抛物线的解析式为y=(x+2)2+1.
2.C 由图象可知抛物线与x轴的交点坐标为(-2,0),(2,0),故设抛物线解析式为y=a(x+2)(x-2)(a≠0).由图象知抛物线经过点(0,3),将(0,3)代入得a(0+2)×(0-2)=3,解得a=-,∴抛物线解析式为y=-(x+2)(x-2)=-x2+3.
3.D 观察函数图象可知s与t为二次函数关系,设s=at2+bt+c(a≠0),将(0,0),(1,4.5),(2,14)代入s=at2+bt+c得解得∴s与t的函数关系式是s=t2+2t.
4.y=2x2+4x+5
解析 已知该抛物线的顶点坐标为(-1,3),可设此抛物线的解析式为y=a(x+1)2+3(a≠0),由于该抛物线和y=2x2的图象开口方向、开口大小都相同,因此a=2,故该抛物线的解析式为y=2(x+1)2+3=2x2+4x+5.
5.y=2x2-8x+5
解析 由题意设该抛物线的解析式为y=a(x-2)2-3(a≠0),将(0,5)代入得5=a(0-2)2-3,解得a=2,∴y=2(x-2)2-3=2x2-8x+5.
6.乙
解析 从乙同学开始出现错误.根据题图可设抛物线的解析式为y=a(x-1)(x+3)(a≠0),由图象知抛物线与y轴交于点(0,3),代入得a(0-1)×(0+3)=3,解得a=-1,∴函数解析式为y=-(x-1)(x+3)=-(x2+2x-3)=-x2-2x+3.
7.解析 (解法1:设一般式)设所求二次函数的表达式为y=ax2+bx+c(a≠0),把A(-1,0),B(3,0),C(4,-5)代入得解得
∴二次函数的表达式为y=-x2+2x+3.
(解法2:设交点式)∵二次函数的图象与x轴的两个交点分别为
A(-1,0),B(3,0),∴可设这个二次函数的表达式为y=a(x+1)(x-3)(a≠0).
∵图象经过点C(4,-5),∴-5=a×5×1,解得a=-1,∴二次函数的表达式为y=-(x+1)(x-3),即y=-x2+2x+3.
(解法3:设顶点式)∵二次函数的图象与x轴的两个交点分别为A
(-1,0),B(3,0),∴这个二次函数的图象的对称轴为直线x=1,设所求抛物线的函数表达式为y=a(x-1)2+k(a≠0),把A(-1,0),C(4,-5)代入得解得∴二次函数的表达式为y=-(x-1)2+4,即y=-x2+2x+3.
8.解析 (1)∵△ABC是等边三角形,∴∠B=60°,∵矩形DEFG的四个顶点分别在等边三角形ABC的边上,∴∠BED=90°,BE=CF=x,
∴EF=4-2x,∴DE=BE·tan 60°=x,∴S=DE·EF=x·(4-2x)=
-2x2+4x(0
9.A 由抛物线y=x2-4x+5=(x-2)2+1知抛物线顶点坐标是(2,1),a=1,由抛物线y=x2-4x+5知C(0,5),∴该抛物线关于点C成中心对称的抛物线的顶点坐标是(-2,9),a=-1,∴该抛物线关于点C成中心对称的抛物线的表达式为y=-(x+2)2+9=-x2-4x+5.
10.A 本题借助二次函数的大致图象确定解析式中二次项系数的值,设计新颖别致.由题图知,A、B、D三点组成的二次函数图象开口向上,a>0;A、B、C三点组成的二次函数图象开口向上,a>0;B、C、D三点组成的二次函数图象开口向下,a<0;A、D、C三点组成的二次函数图象开口向下,a<0,即只需比较A、B、D三点组成的抛物线和A、B、C三点组成的抛物线即可.设A、B、C三点组成的抛物线解析式为y=a1x2+b1x+c1(a1≠0),把A(0,2),B(1,0),C(3,1)代入得解得a1=.设A、B、D三点组成的抛物线解析式为y=ax2+bx+c(a≠0),把A(0,2),B(1,0),D(2,3)代入得解得a=,∵<,∴a的最大值为.
11.答案不唯一,如y=-x2+1
解析 由题意得b=0,a<0,c>0,∴这个二次函数的解析式可以是y=
-x2+1.(答案不唯一)
12.解析 (1)把A(-1,0)、B(3,0)代入y=x2+bx+c得解得∴抛物线的解析式为y=x2-2x-3,∵y=x2-2x-3=(x-1)2-4,∴顶点坐标为(1,-4).
(2)∵A(-1,0)、B(3,0),∴AB=3-(-1)=4,设P点坐标为(t,t2-2t-3),∵S△PAB=10,∴×4×|t2-2t-3|=10,∴t2-2t-3=±5,当t2-2t-3=5时,解得t1=
-2,t2=4,此时P点坐标为(-2,5)或(4,5);当t2-2t-3=-5时,方程没有实数解,故P点坐标为(-2,5)或(4,5).
13.解析 (1)对称轴为直线x=-=1.
(2)∵该二次函数的图象开口向上,对称轴为直线x=1,且当-1≤x≤4时,y的最大值是5,∴当x=4时,y=5,∴代入得,16a-8a+2a=5,∴a=,∴抛物线的解析式为y=x2-x+1.
(3)∵对称轴为直线x=1,∴x=-1与x=3时的y值相等,∵x2>3时,均满足y1
②当a>0时,抛物线开口向上,如图2,当x2取大于3的任何实数时,均满足y1
图2
综上所述,当x2取大于3的任何实数时,均满足y1
14.解析 (1)由题意得,抛物线的表达式为y=a(x+1)×(x-3)=a(x2-2x-3),将C(0,3)代入得-3a=3,解得a=-1,故抛物线的表达式为y=-x2+2x+3.
(2)由点B、C的坐标得直线BC的表达式为y=-x+3,如图,过点P作y轴的平行线交CB于点H,连结PC,PB,设点P(x,-x2+2x+3),则点H(x,
-x+3),∴△PBC的面积=S△PHC+S△PHB=PH·OB=(-x2+3x)=
-+,∵a=-<0,∴当x=时△PBC的面积有最大值,为,此时点P.
(3)存在.理由:由(1)知抛物线的解析式为y=-x2+2x+3,∴对称轴为直线x=1,设点M(1,t),N(x,y),分情况求解如下:
①若BC为菱形BCMN的边,则BC2=CM2,即18=12+(t-3)2,解得t1=+3,t2=-+3,∵∴x=4,y=t-3,∴N1(4,),N2(4,
-).
②若BC为菱形BCNM的边,则BC2=BM2,即18=(3-1)2+t2,解得t3=,t4=-,
∵∴x=-2,y=3+t,
∴N3(-2,+3),N4(-2,-+3).
综上所述,点N的坐标为(4,-)或(4,)或(-2,+3)或(-2,-+3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
