2024华东师大版数学九年级下学期课时练--27.1.1 圆的基本元素 27.1.2 圆的对称性(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--27.1.1 圆的基本元素 27.1.2 圆的对称性(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 581.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
第27章 圆
27.1 圆的认识
27.1.1 圆的基本元素
27.1.2 圆的对称性
基础过关全练
知识点1 圆的定义
1.下列条件中,可以确定一个圆的是( )
A.半径是1 cm
B.圆心在数轴的原点处
C.半径是1 cm,且经过点P
D.圆心在数轴的原点处,且直径是2 cm
知识点2 圆的有关概念
2.【跨学科·体育与健康】【教材变式·P37T2】如图所示,体育课上,小明掷铅球的成绩为6.4 m,他掷出的铅球落在( )
A.区域① B.区域②
C.区域③ D.区域④
3.【一题多解】(2023湖南衡阳船山实验中学期末)如图,若BC是☉A的弦,∠BAC=90°,BC=10,则△ABC的面积为 .
知识点3 圆的对称性,圆心角、弧、弦之间的关系
4.(2023海南海口琼山期末)如图,在☉O中,=,∠AOB=45°,则∠COD=( )
A.60° B.45° C.30° D.40°
5.(2023天津南开期中)如图,AB是☉O的直径,点E在☉O上,点D,C是的三等分点,∠COD=34°,则∠AOE的度数是( )
A.78° B.68° C.58° D.56°
6.【中华优秀传统文化】太极图是以黑、白两个鱼形纹组成的圆形图案,展现了一种互相转化、相对统一的形式美,是我国民族图案所特有的“美”的结构.如图所示的是一幅太极图,若大圆的半径为1 cm,则阴影区域的面积为 cm2.
7.(2023陕西西安理工大学附中期中)已知:如图,C,D是以AB为直径的☉O上的两点,且OD∥BC.
(1)求证:AD=DC.
(2)点C是的中点,求∠BOD的度数.
知识点4 垂径定理及其推论
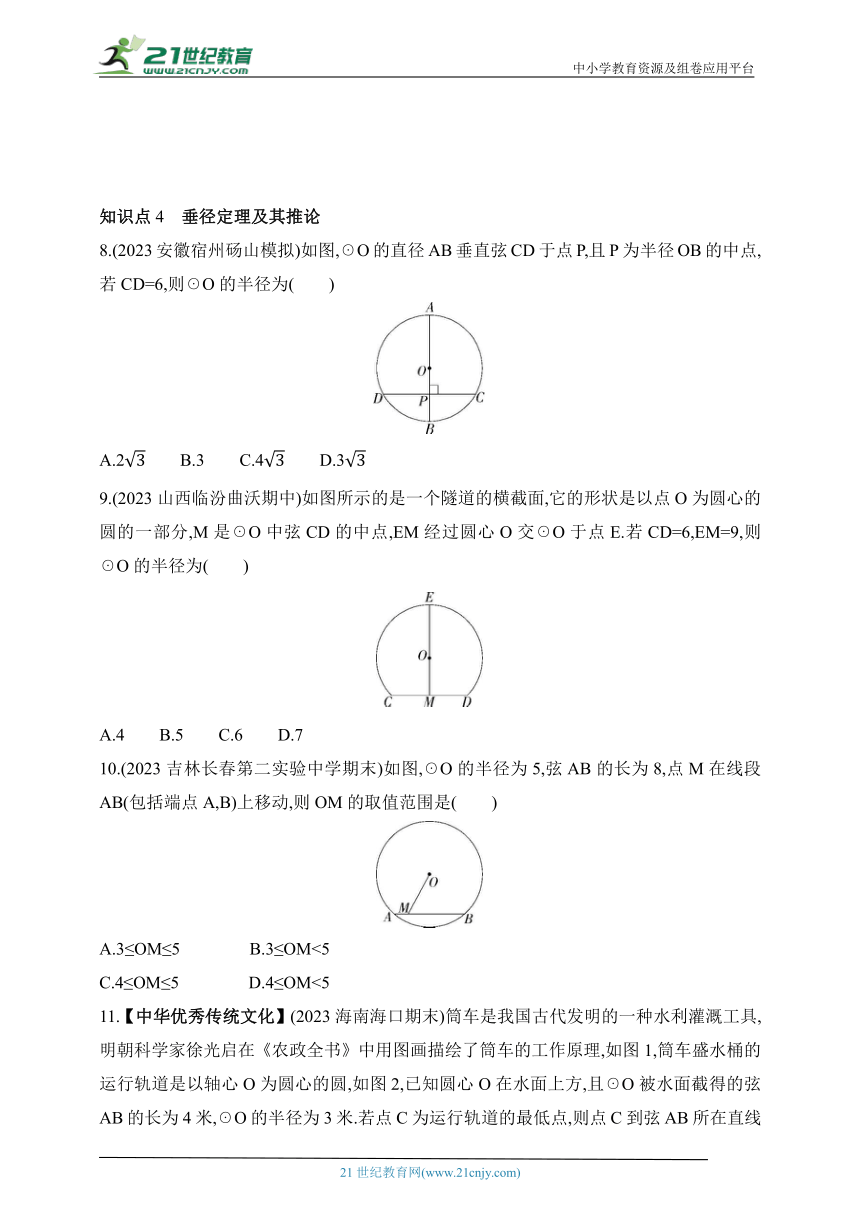
8.(2023安徽宿州砀山模拟)如图,☉O的直径AB垂直弦CD于点P,且P为半径OB的中点,若CD=6,则☉O的半径为( )
A.2 B.3 C.4 D.3
9.(2023山西临汾曲沃期中)如图所示的是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,M是☉O中弦CD的中点,EM经过圆心O交☉O于点E.若CD=6,EM=9,则☉O的半径为( )
A.4 B.5 C.6 D.7
10.(2023吉林长春第二实验中学期末)如图,☉O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM的取值范围是( )
A.3≤OM≤5 B.3≤OM<5
C.4≤OM≤5 D.4≤OM<5
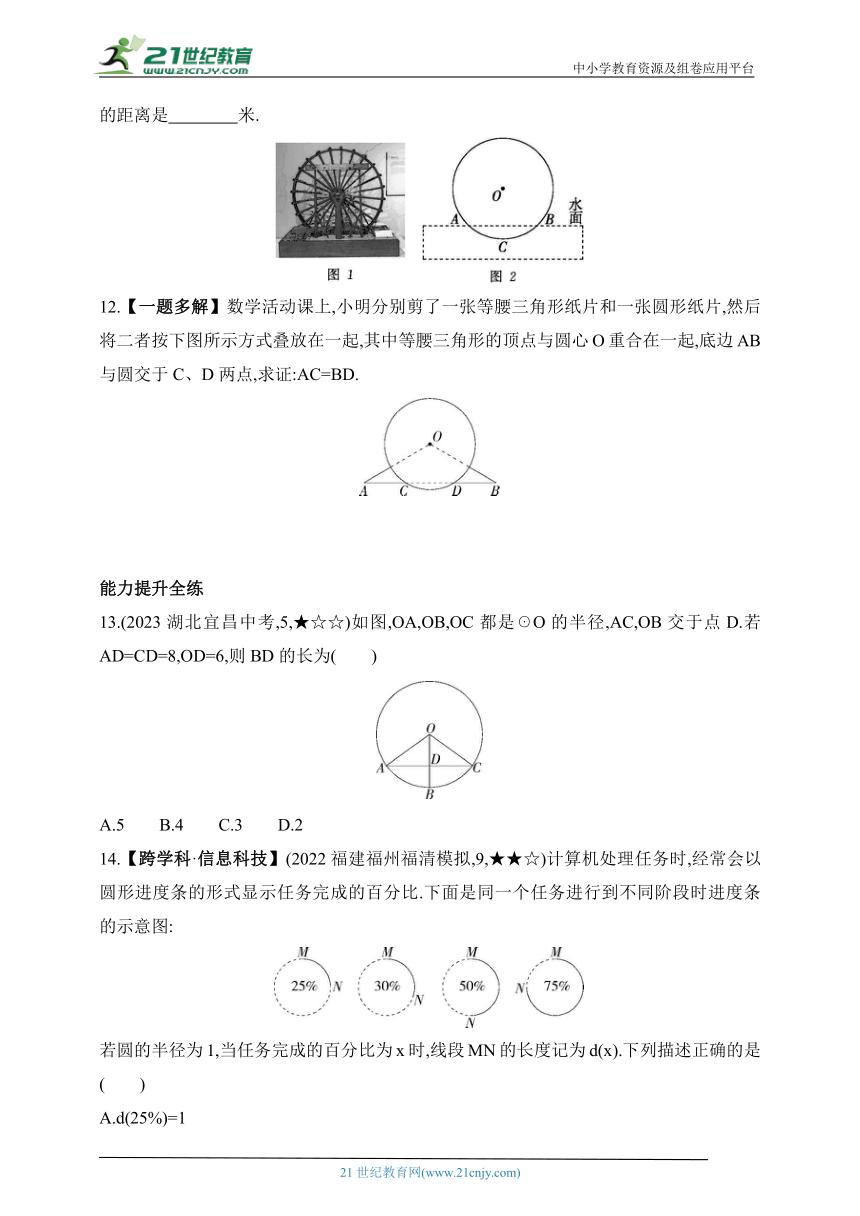
11.【中华优秀传统文化】(2023海南海口期末)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且☉O被水面截得的弦AB的长为4米,☉O的半径为3米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是 米.
12.【一题多解】数学活动课上,小明分别剪了一张等腰三角形纸片和一张圆形纸片,然后将二者按下图所示方式叠放在一起,其中等腰三角形的顶点与圆心O重合在一起,底边AB与圆交于C、D两点,求证:AC=BD.
能力提升全练
13.(2023湖北宜昌中考,5,★☆☆)如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为( )
A.5 B.4 C.3 D.2
14.【跨学科·信息科技】(2022福建福州福清模拟,9,★★☆)计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆的半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
15.【一题多变·已知弧间的关系,确定弦间的关系】
(2023四川宜宾翠屏期中,15,★☆☆)如图,在☉O中,==,连结AB,BC,AC,CD,则AC 2CD(填“>”“<”或“=”).
[变式·已知弦间的关系,确定弧间的关系](2023福建漳州康桥学校月考,16,★☆☆)如图,在☉O中,AB=2CD,那么 2(填“>”“<”或“=”).
16.【数学文化】(2023山东东营中考,16,★★☆)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何 (一尺等于10寸)”转化为现在的数学语言表达就是:如图,CD为☉O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长为 寸.
17.【教材变式·P72T4·四边形变三角形】(2023吉林长春汽开区模拟,11,★★☆)如图,AB为☉O的直径,△PAB的边PA,PB与☉O的交点分别为C、D.若==,则∠P的大小为 度.
18.(2023上海中考,21,★★☆)如图,在☉O中,弦AB的长为8,点C在BO的延长线上,且cos∠ABC=,OC=OB.
(1)求☉O的半径;
(2)求∠BAC的正切值.
19.【中华优秀传统文化】(2023浙江绍兴诸暨滨江初中教育集团模拟,24,★★☆)好山好水好绍兴,石拱桥在绍兴处处可见,小明要帮船夫计算一艘货船能否安全通过一座圆弧形的拱桥,现测得桥下水面AB的宽度为16 m时,拱顶高出水面4 m,货船宽12 m,船舱顶部为矩形并高出水面3 m.
(1)请你帮助小明求此圆弧形拱桥的半径;
(2)小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗 说说你的理由.
素养探究全练
20.【模型观念】不过圆心的直线l交☉O于C,D两点,AB是☉O的直径,AE⊥l于E,BF⊥l于F.
(1)在如图所示的三个圆中,分别画出满足上述条件的具有不同位置关系的图形;
(2)请你观察(1)中所画的图形,写出一个各图形都具有的两条线段相等的结论(除OA=OB外);(不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程)
(3)请你选择(1)中的一个图形,证明(2)所得出的结论.
答案全解全析
基础过关全练
1.D 直径确定圆的大小,圆心确定圆的位置.
2.D ∵小明掷铅球的成绩为6.4 m,且6<6.4<7,∴他掷出的铅球落在区域④.
3.25
解析 (解法1:以AB为底)在☉A中,AB=AC,∠BAC=90°,∴∠B=∠C=45°,∴AB=10sin 45°=10×=5,∴S△ABC=AB·AC=×5×5=25.
(解法2:以BC为底)如图,过点A作AD⊥BC于点D,∵AB=AC,∴BD=CD,∵∠BAC=90°,∴AD=BC=5,∴S△ABC=BC·AD=×10×5=25.
4.B ∵=,∴∠COD=∠AOB=45°.
5.A ∵点D、C是的三等分点,∴==,∴∠BOC=∠COD=∠DOE=34°,∴∠AOE=180°-3×34°=78°.
6.
解析 根据题意知,题图中阴影区域的面积为×π×12=(cm2).
7.解析 (1)证明:如图,连结OC,∵OD∥BC,∴∠1=∠B,∠2=∠3,∵OB=OC,∴∠B=∠3,∴∠1=∠2,∴AD=DC.
(2)∵点C是的中点,∴=,∴∠AOC=90°.由(1)知AD=CD,∴∠AOD=∠AOC=45°,∴∠BOD=180°-∠AOD=135°.
8.A 如图,连结OD,设圆的半径是r,∵P是OB的中点,∴OP=r,∵AB⊥CD,∴PD=CD=×6=3,在Rt△ODP中,OD2=OP2+PD2,∴r2=+32,解得r=2(舍负),∴☉O的半径是2.
9.B 如图,连结OC,∵M是☉O中弦CD的中点,∴EM⊥CD,∵CD=6,∴CM=CD=3,设OC=OE=x,则OM=9-x,在Rt△COM中,OC2=CM2+OM2,即x2=32+(9-x)2,解得x=5,∴☉O的半径为5.
10.A 当M与A或B重合时,OM取得最大值,即圆的半径5,当OM⊥AB时,OM取得最小值,即=3,故OM的取值范围是3≤OM≤5.
11.(3-)
解析 根据题意和圆的性质知点C为的中点,如图,连结OA,连结OC交AB于D,则OC⊥AB,∴AD=BD=AB=2米,在Rt△OAD中,OA=3米,AD=2米,∴OD==(米),∴CD=OC-OD=(3-)米,即点C到弦AB所在直线的距离是(3-)米.
12.证明 (证法1:利用三角形全等)如图,过点O作OE⊥AB于点E,在☉O中,∵OE⊥CD,∴CE=DE.在Rt△AOE和Rt△BOE中,∵OA=OB,OE=OE,∴Rt△AOE≌Rt△BOE,∴AE=BE,∴AE-CE=BE-DE,∴AC=BD.
(证法2:利用等腰三角形的性质)如图,过点O作OE⊥AB于点E,在☉O中,∵OE⊥CD,∴CE=DE.∵OA=OB,OE⊥AB,∴AE=BE,∴AE-CE=BE-DE,∴AC=BD.
能力提升全练
13.B ∵AD=CD=8,∴OB⊥AC,在Rt△AOD中,OA===10,∴OB=10,∴BD=10-6=4.
14.D 选项A中,d(25%)=>1;选项B中,当x>50%时,0≤d(x)<2;选项C中,当x1>x2时,d(x1)与d(x2)可能相等,也可能不相等;选项D中,当x1+x2=100%时,d(x1)=d(x2).故选D.
15.<
解析 在同圆或等圆中,弧的倍数不等于弦的倍数.∵==,∴AB=BC=CD,∵AC[变式] 答案 >
解析 如图,过点O作OM⊥AB,垂足为N,交☉O于点M,连结MA,MB,由垂径定理得AN=BN,=,∵AB=2CD,∴AN=BN=CD,∵MA>AN,∴MA>CD,∴>,∴2>2,即>2.
16.26
解析 如图,连结OA,设☉O的半径是r寸,∵直径CD⊥AB,∴AE=AB=×10=5(寸),∵CE=1寸,∴OE=(r-1)寸,∵OA2=OE2+AE2,∴r2=(r-1)2+52,∴r=13,∴直径CD的长为2×13=26寸.
17.60
解析 如图,连结OC、OD,∵==,∴∠AOC=∠COD=∠DOB=60°,∵OA=OC,OB=OD,∴△AOC和△BOD都是等边三角形,∴∠A=60°,∠B=60°,∴∠P=60°.
18.解析 (1)如图,过点O作OD⊥AB,垂足为D,∵AB=8,∴AD=BD=AB=4,在Rt△OBD中,cos∠ABC=,∴OB===5,∴☉O的半径为5.
(2)如图,过点C作CE⊥AB,垂足为E,∵OC=OB,OB=5,∴BC=OB=7.5,∵OD⊥AB,∴OD∥CE,∴=,
∴=,∴BE=6,∴AE=AB-BE=8-6=2,在Rt△BCE中,CE===4.5,在Rt△ACE中,tan∠BAC===,∴∠BAC的正切值为.
19.解析 (1)如图,连结OB.∵OC⊥AB,∴D为AB中点,∵AB=16 m,∴BD=AB=8 m.设OB=OC=r m,则OD=(r-4)m.在Rt△BOD中,根据勾股定理得r2=(r-4)2+82,解得r=10,故此圆弧形拱桥的半径为10 m.
(2)不能.理由:如图,令矩形MNGF为船舱顶部,设MN与OC交于点E,连结ON,∵CD=4 m,船舱顶部MNGF为矩形并高出水面
3 m,∴CE=4-3=1(m),∴OE=r-CE=10-1=9(m),在Rt△OEN中,EN2=ON2-OE2=102-92=19,∴EN= m.∴MN=2EN=2 m<12 m,∴此货船不能顺利通过这座拱桥.
素养探究全练
20.解析 答案不唯一.
(1)如图所示:
(2)EC=FD(或ED=FC).
(3)以(1)中所画的第一个图形为例来证明EC=FD.
证明:过O作OH⊥l于H(图略),∵AE⊥l,BF⊥l,∴AE∥OH∥BF,又∵OA=OB,∴EH=HF.由垂径定理可得CH=DH,∴EH-CH=HF-DH,即EC=FD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
第27章 圆
27.1 圆的认识
27.1.1 圆的基本元素
27.1.2 圆的对称性
基础过关全练
知识点1 圆的定义
1.下列条件中,可以确定一个圆的是( )
A.半径是1 cm
B.圆心在数轴的原点处
C.半径是1 cm,且经过点P
D.圆心在数轴的原点处,且直径是2 cm
知识点2 圆的有关概念
2.【跨学科·体育与健康】【教材变式·P37T2】如图所示,体育课上,小明掷铅球的成绩为6.4 m,他掷出的铅球落在( )
A.区域① B.区域②
C.区域③ D.区域④
3.【一题多解】(2023湖南衡阳船山实验中学期末)如图,若BC是☉A的弦,∠BAC=90°,BC=10,则△ABC的面积为 .
知识点3 圆的对称性,圆心角、弧、弦之间的关系
4.(2023海南海口琼山期末)如图,在☉O中,=,∠AOB=45°,则∠COD=( )
A.60° B.45° C.30° D.40°
5.(2023天津南开期中)如图,AB是☉O的直径,点E在☉O上,点D,C是的三等分点,∠COD=34°,则∠AOE的度数是( )
A.78° B.68° C.58° D.56°
6.【中华优秀传统文化】太极图是以黑、白两个鱼形纹组成的圆形图案,展现了一种互相转化、相对统一的形式美,是我国民族图案所特有的“美”的结构.如图所示的是一幅太极图,若大圆的半径为1 cm,则阴影区域的面积为 cm2.
7.(2023陕西西安理工大学附中期中)已知:如图,C,D是以AB为直径的☉O上的两点,且OD∥BC.
(1)求证:AD=DC.
(2)点C是的中点,求∠BOD的度数.
知识点4 垂径定理及其推论
8.(2023安徽宿州砀山模拟)如图,☉O的直径AB垂直弦CD于点P,且P为半径OB的中点,若CD=6,则☉O的半径为( )
A.2 B.3 C.4 D.3
9.(2023山西临汾曲沃期中)如图所示的是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,M是☉O中弦CD的中点,EM经过圆心O交☉O于点E.若CD=6,EM=9,则☉O的半径为( )
A.4 B.5 C.6 D.7
10.(2023吉林长春第二实验中学期末)如图,☉O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM的取值范围是( )
A.3≤OM≤5 B.3≤OM<5
C.4≤OM≤5 D.4≤OM<5
11.【中华优秀传统文化】(2023海南海口期末)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且☉O被水面截得的弦AB的长为4米,☉O的半径为3米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是 米.
12.【一题多解】数学活动课上,小明分别剪了一张等腰三角形纸片和一张圆形纸片,然后将二者按下图所示方式叠放在一起,其中等腰三角形的顶点与圆心O重合在一起,底边AB与圆交于C、D两点,求证:AC=BD.
能力提升全练
13.(2023湖北宜昌中考,5,★☆☆)如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为( )
A.5 B.4 C.3 D.2
14.【跨学科·信息科技】(2022福建福州福清模拟,9,★★☆)计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆的半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
15.【一题多变·已知弧间的关系,确定弦间的关系】
(2023四川宜宾翠屏期中,15,★☆☆)如图,在☉O中,==,连结AB,BC,AC,CD,则AC 2CD(填“>”“<”或“=”).
[变式·已知弦间的关系,确定弧间的关系](2023福建漳州康桥学校月考,16,★☆☆)如图,在☉O中,AB=2CD,那么 2(填“>”“<”或“=”).
16.【数学文化】(2023山东东营中考,16,★★☆)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何 (一尺等于10寸)”转化为现在的数学语言表达就是:如图,CD为☉O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长为 寸.
17.【教材变式·P72T4·四边形变三角形】(2023吉林长春汽开区模拟,11,★★☆)如图,AB为☉O的直径,△PAB的边PA,PB与☉O的交点分别为C、D.若==,则∠P的大小为 度.
18.(2023上海中考,21,★★☆)如图,在☉O中,弦AB的长为8,点C在BO的延长线上,且cos∠ABC=,OC=OB.
(1)求☉O的半径;
(2)求∠BAC的正切值.
19.【中华优秀传统文化】(2023浙江绍兴诸暨滨江初中教育集团模拟,24,★★☆)好山好水好绍兴,石拱桥在绍兴处处可见,小明要帮船夫计算一艘货船能否安全通过一座圆弧形的拱桥,现测得桥下水面AB的宽度为16 m时,拱顶高出水面4 m,货船宽12 m,船舱顶部为矩形并高出水面3 m.
(1)请你帮助小明求此圆弧形拱桥的半径;
(2)小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗 说说你的理由.
素养探究全练
20.【模型观念】不过圆心的直线l交☉O于C,D两点,AB是☉O的直径,AE⊥l于E,BF⊥l于F.
(1)在如图所示的三个圆中,分别画出满足上述条件的具有不同位置关系的图形;
(2)请你观察(1)中所画的图形,写出一个各图形都具有的两条线段相等的结论(除OA=OB外);(不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程)
(3)请你选择(1)中的一个图形,证明(2)所得出的结论.
答案全解全析
基础过关全练
1.D 直径确定圆的大小,圆心确定圆的位置.
2.D ∵小明掷铅球的成绩为6.4 m,且6<6.4<7,∴他掷出的铅球落在区域④.
3.25
解析 (解法1:以AB为底)在☉A中,AB=AC,∠BAC=90°,∴∠B=∠C=45°,∴AB=10sin 45°=10×=5,∴S△ABC=AB·AC=×5×5=25.
(解法2:以BC为底)如图,过点A作AD⊥BC于点D,∵AB=AC,∴BD=CD,∵∠BAC=90°,∴AD=BC=5,∴S△ABC=BC·AD=×10×5=25.
4.B ∵=,∴∠COD=∠AOB=45°.
5.A ∵点D、C是的三等分点,∴==,∴∠BOC=∠COD=∠DOE=34°,∴∠AOE=180°-3×34°=78°.
6.
解析 根据题意知,题图中阴影区域的面积为×π×12=(cm2).
7.解析 (1)证明:如图,连结OC,∵OD∥BC,∴∠1=∠B,∠2=∠3,∵OB=OC,∴∠B=∠3,∴∠1=∠2,∴AD=DC.
(2)∵点C是的中点,∴=,∴∠AOC=90°.由(1)知AD=CD,∴∠AOD=∠AOC=45°,∴∠BOD=180°-∠AOD=135°.
8.A 如图,连结OD,设圆的半径是r,∵P是OB的中点,∴OP=r,∵AB⊥CD,∴PD=CD=×6=3,在Rt△ODP中,OD2=OP2+PD2,∴r2=+32,解得r=2(舍负),∴☉O的半径是2.
9.B 如图,连结OC,∵M是☉O中弦CD的中点,∴EM⊥CD,∵CD=6,∴CM=CD=3,设OC=OE=x,则OM=9-x,在Rt△COM中,OC2=CM2+OM2,即x2=32+(9-x)2,解得x=5,∴☉O的半径为5.
10.A 当M与A或B重合时,OM取得最大值,即圆的半径5,当OM⊥AB时,OM取得最小值,即=3,故OM的取值范围是3≤OM≤5.
11.(3-)
解析 根据题意和圆的性质知点C为的中点,如图,连结OA,连结OC交AB于D,则OC⊥AB,∴AD=BD=AB=2米,在Rt△OAD中,OA=3米,AD=2米,∴OD==(米),∴CD=OC-OD=(3-)米,即点C到弦AB所在直线的距离是(3-)米.
12.证明 (证法1:利用三角形全等)如图,过点O作OE⊥AB于点E,在☉O中,∵OE⊥CD,∴CE=DE.在Rt△AOE和Rt△BOE中,∵OA=OB,OE=OE,∴Rt△AOE≌Rt△BOE,∴AE=BE,∴AE-CE=BE-DE,∴AC=BD.
(证法2:利用等腰三角形的性质)如图,过点O作OE⊥AB于点E,在☉O中,∵OE⊥CD,∴CE=DE.∵OA=OB,OE⊥AB,∴AE=BE,∴AE-CE=BE-DE,∴AC=BD.
能力提升全练
13.B ∵AD=CD=8,∴OB⊥AC,在Rt△AOD中,OA===10,∴OB=10,∴BD=10-6=4.
14.D 选项A中,d(25%)=>1;选项B中,当x>50%时,0≤d(x)<2;选项C中,当x1>x2时,d(x1)与d(x2)可能相等,也可能不相等;选项D中,当x1+x2=100%时,d(x1)=d(x2).故选D.
15.<
解析 在同圆或等圆中,弧的倍数不等于弦的倍数.∵==,∴AB=BC=CD,∵AC
解析 如图,过点O作OM⊥AB,垂足为N,交☉O于点M,连结MA,MB,由垂径定理得AN=BN,=,∵AB=2CD,∴AN=BN=CD,∵MA>AN,∴MA>CD,∴>,∴2>2,即>2.
16.26
解析 如图,连结OA,设☉O的半径是r寸,∵直径CD⊥AB,∴AE=AB=×10=5(寸),∵CE=1寸,∴OE=(r-1)寸,∵OA2=OE2+AE2,∴r2=(r-1)2+52,∴r=13,∴直径CD的长为2×13=26寸.
17.60
解析 如图,连结OC、OD,∵==,∴∠AOC=∠COD=∠DOB=60°,∵OA=OC,OB=OD,∴△AOC和△BOD都是等边三角形,∴∠A=60°,∠B=60°,∴∠P=60°.
18.解析 (1)如图,过点O作OD⊥AB,垂足为D,∵AB=8,∴AD=BD=AB=4,在Rt△OBD中,cos∠ABC=,∴OB===5,∴☉O的半径为5.
(2)如图,过点C作CE⊥AB,垂足为E,∵OC=OB,OB=5,∴BC=OB=7.5,∵OD⊥AB,∴OD∥CE,∴=,
∴=,∴BE=6,∴AE=AB-BE=8-6=2,在Rt△BCE中,CE===4.5,在Rt△ACE中,tan∠BAC===,∴∠BAC的正切值为.
19.解析 (1)如图,连结OB.∵OC⊥AB,∴D为AB中点,∵AB=16 m,∴BD=AB=8 m.设OB=OC=r m,则OD=(r-4)m.在Rt△BOD中,根据勾股定理得r2=(r-4)2+82,解得r=10,故此圆弧形拱桥的半径为10 m.
(2)不能.理由:如图,令矩形MNGF为船舱顶部,设MN与OC交于点E,连结ON,∵CD=4 m,船舱顶部MNGF为矩形并高出水面
3 m,∴CE=4-3=1(m),∴OE=r-CE=10-1=9(m),在Rt△OEN中,EN2=ON2-OE2=102-92=19,∴EN= m.∴MN=2EN=2 m<12 m,∴此货船不能顺利通过这座拱桥.
素养探究全练
20.解析 答案不唯一.
(1)如图所示:
(2)EC=FD(或ED=FC).
(3)以(1)中所画的第一个图形为例来证明EC=FD.
证明:过O作OH⊥l于H(图略),∵AE⊥l,BF⊥l,∴AE∥OH∥BF,又∵OA=OB,∴EH=HF.由垂径定理可得CH=DH,∴EH-CH=HF-DH,即EC=FD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
