2024华东师大版数学九年级下学期课时练--27.1.3 圆周角(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--27.1.3 圆周角(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 560.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
第27章 圆
27.1.3 圆周角
基础过关全练
知识点1 圆周角及其定理与推论
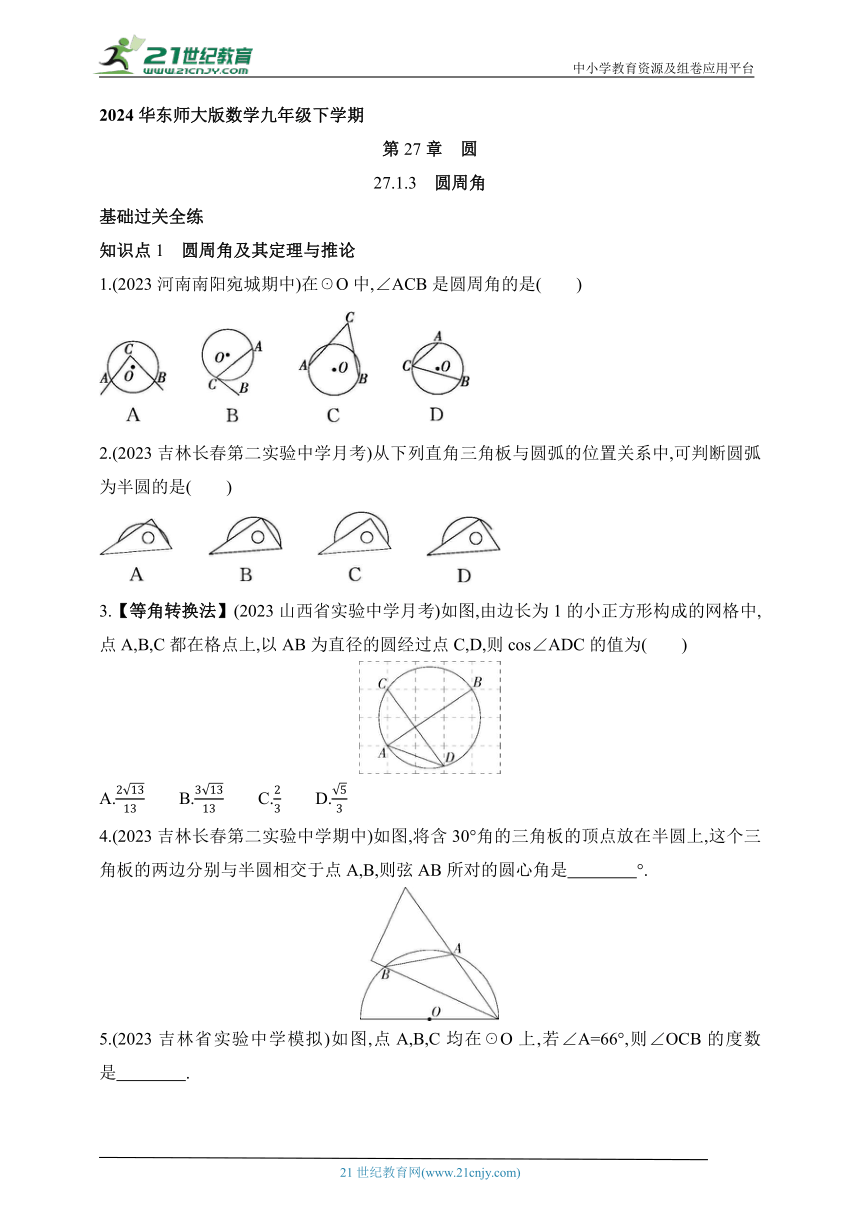
1.(2023河南南阳宛城期中)在☉O中,∠ACB是圆周角的是( )
2.(2023吉林长春第二实验中学月考)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
3.【等角转换法】(2023山西省实验中学月考)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则cos∠ADC的值为( )
A. B. C. D.
4.(2023吉林长春第二实验中学期中)如图,将含30°角的三角板的顶点放在半圆上,这个三角板的两边分别与半圆相交于点A,B,则弦AB所对的圆心角是 °.
5.(2023吉林省实验中学模拟)如图,点A,B,C均在☉O上,若∠A=66°,则∠OCB的度数是 .
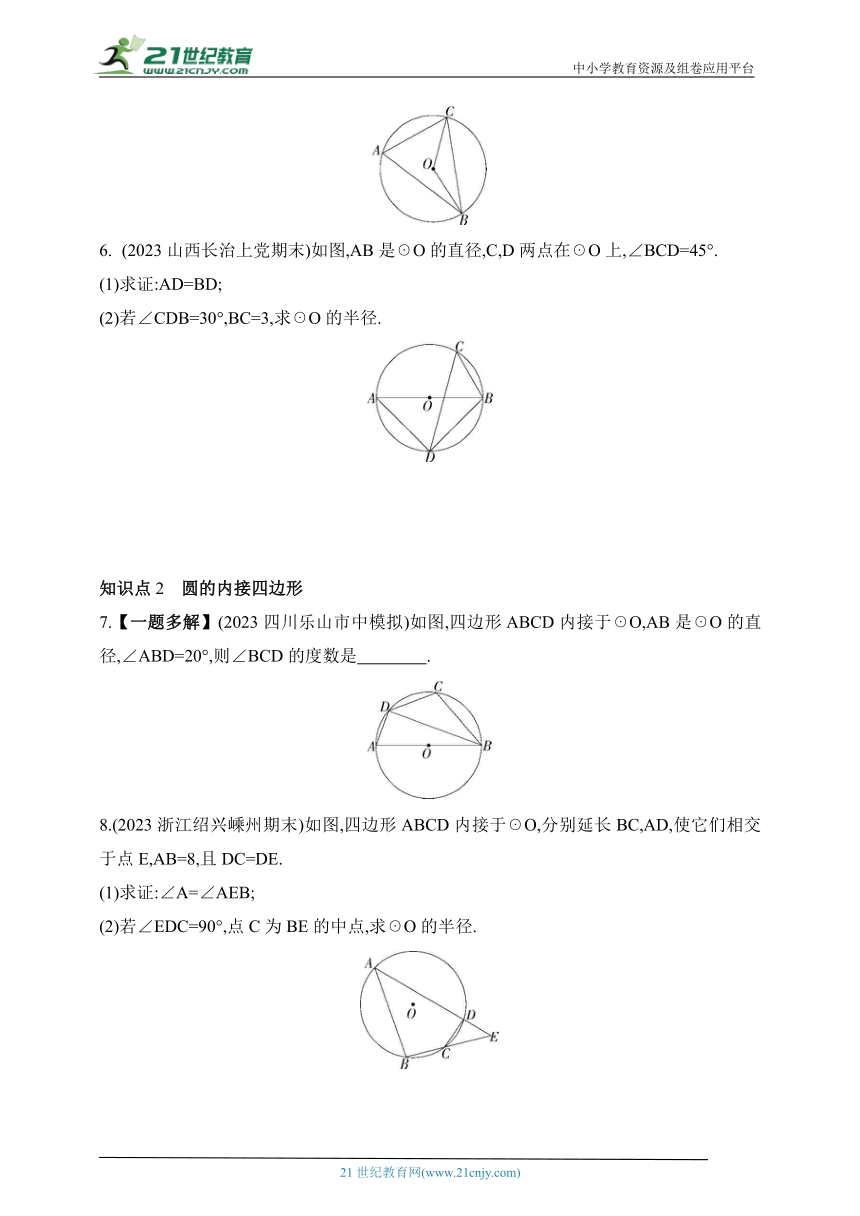
(2023山西长治上党期末)如图,AB是☉O的直径,C,D两点在☉O上,∠BCD=45°.
(1)求证:AD=BD;
(2)若∠CDB=30°,BC=3,求☉O的半径.
知识点2 圆的内接四边形
7.【一题多解】(2023四川乐山市中模拟)如图,四边形ABCD内接于☉O,AB是☉O的直径,∠ABD=20°,则∠BCD的度数是 .
8.(2023浙江绍兴嵊州期末)如图,四边形ABCD内接于☉O,分别延长BC,AD,使它们相交于点E,AB=8,且DC=DE.
(1)求证:∠A=∠AEB;
(2)若∠EDC=90°,点C为BE的中点,求☉O的半径.
能力提升全练
9.(2023山东泰安中考,7,★☆☆)如图,AB是☉O的直径,D,C是☉O上的点,∠ADC=115°,则∠BAC的度数是( )
A.25° B.30° C.35° D.40°
10.(2023吉林中考,6,★☆☆)如图,AB,AC是☉O的弦,OB,OC是☉O的半径,点P为OB上任意一点(点P不与点B重合),连结CP.若∠BAC=70°,则∠BPC的度数可能是( )
A.70° B.105° C.125° D.155°
11.(2023内蒙古赤峰中考,10,★★☆)如图,圆内接四边形ABCD中,∠BCD=105°,连结OB,OC,OD,BD,∠BOC=2∠COD,则∠CBD的度数是( )
A.25° B.30°
C.35° D.40°
12.【一题多变·给出圆,研究点在圆上的运动】(2023湖南永州模拟,17,★★☆)如图,☉O上有两定点A、B,点P是☉O上一动点(不与A、B两点重合),若∠OAB=30°,则∠APB的度数是 .
[变式·构造圆,研究点在圆上的运动](2023湖南衡阳船山实验中学模拟,20,★☆☆)在平面直角坐标系中,已知点A(4,0)、B(-6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为 .
13.【新考向·尺规作图】【数学文化】(2023山西临汾侯马模拟,21,★★☆)阅读以下材料,并按要求完成相应的关于圆的任务.
关于圆的引理
在《阿基米德全集》的《引理集》中,记述了古希腊的数学家、物理学家阿基米德提出的六个关于圆的引理,其中第二个引理为:如图,在半圆O中,P是上的任意一点,PN⊥直径AB于点N,D在直径AB上,且AN=ND,在上取一点Q,使=,连结BQ,则BQ=BD.
任务:
(1)尺规作图:请根据材料,在图中补全图形;(保留作图痕迹,标明字母,不写作法)
(2)善思小组的同学尝试证明该引理,请按照下面的证明思路,写出该证明的剩余部分.
证明:连结PA,PD,PQ,QD.
……
素养探究全练
14.【推理能力】(2023湖北天门模拟)如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连结AC并延长,与BD的延长线相交于点E,连结CD.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF·AF=FO·AH;
②若圆的半径为2,BD=1,如图3,求AC的长.
答案全解全析
基础过关全练
1.D 选项A、C中,∠ACB的顶点不在圆上,故不是圆周角;选项B中,∠ACB的两边只有一边与圆相交,故不是圆周角.故选D.
2.B ∵直径所对的圆周角等于直角,∴从选项中,可判断圆弧为半圆的是B.
3.B ∵AB为直径,∴∠ACB=90°,∵点A,B,C,D都在同一个圆上,=,∴∠ADC=∠ABC,在Rt△ABC中,cos∠ABC====cos∠ADC.
方法解读 当与已知角有关的问题不易求解时,可先尝试对图形进行分析,能否通过转化的思想将已知角进行转化,从而实现解决问题的目的.常见的等角转换的方法有:等边对等角;两直线平行,同位角、内错角相等;全等或相似三角形的对应角相等;同(等)角的余角、补角相等;平行四边形的对角相等;在同(等)圆中,同弧或等弧所对的圆周角相等等.
4.60
解析 如图,连结OA,OB,由圆周角定理得∠AOB=2∠ACB,∵∠ACB=30°,∴∠AOB=60°.
5.24°
解析 ∵∠A与∠BOC所对弧相同,∴∠BOC=2∠A=2×66°=132°,∵OB=OC,∴∠OBC=∠OCB,∴∠OCB=×(180°-132°)=24°.
6.解析 (1)证明:∵∠DCB=45°,∴∠DAB=∠DCB=45°,∵AB是☉O的直径,∴∠ADB=90°,∴∠ABD=45°,∴∠DAB=∠ABD,∴AD=BD.
(2)如图,连结AC,∵AB是☉O的直径,∴∠ACB=90°,∵∠CAB=∠CDB=30°,BC=3,∴AB=6,∴☉O的半径为3.
7.110°
解析 (解法1:圆周角定理的推论)∵AB是☉O的直径,∴∠ADB=90°,∴∠ABD+∠A=90°.∵∠ABD=20°,∴∠A=70°.∵四边形ABCD是圆内接四边形,∴∠A+∠BCD=180°,∴∠BCD=110°.
(解法2:等腰三角形的性质)如图,连结OD,∵∠AOD=2∠ABD=40°,OA=OD,∴∠OAD=∠ODA=(180°-∠AOD)=70°.∵四边形ABCD是圆内接四边形,∴∠OAD+∠BCD=180°,∴∠BCD=110°.
(解法3:圆周角定理)如图,连结AC,∵AB是☉O的直径,∴∠ACB=90°.∵=,∴∠ACD=∠ABD=20°,∴∠BCD=∠ACD+∠ACB=20°+90°=110°.
8.解析 (1)证明:∵四边形ABCD内接于☉O,∴∠A+∠BCD=180°,∵∠BCD+∠DCE=180°,∴∠A=∠DCE,∵DC=DE,∴∠E=∠DCE,∴∠A=∠AEB.
(2)如图,连结AC,∵∠EDC=90°,∴∠ADC=90°,∴AC是☉O的直径,∴∠ABC=90°,∵∠BAE=∠AEB,∴AB=BE,∵AB=8,∴BE=8,∵点C为BE的中点,∴BC=BE=4,在Rt△ABC中,AC===4,∴☉O的半径为2.
能力提升全练
9.A 如图,连结OC,∵∠ADC=115°,∴优弧所对的圆心角为2×115°=230°,∴∠BOC=230°-180°=50°,∴∠BAC=∠BOC=25°.
10.D ∵∠BAC=70°,∴∠BOC=2∠BAC=140°,∴∠BPC=∠BOC+∠OCP=140°+
∠OCP≥140°.故选D.
11.A ∵四边形ABCD是☉O的内接四边形,∴∠A+∠BCD=180°,∵∠BCD=105°,∴∠A=75°,∴∠BOD=2∠A=150°,∵∠BOC=2∠COD,∴∠BOD=3∠COD=150°,∴∠COD=50°,
∴∠CBD=∠COD=25°.
12.60°或120°
解析 如图,连结OB.∵OA=OB,∴∠OAB=∠OBA=30°,∴∠AOB=120°,分两种情况求解如下:
(1)当点P在优弧上时,∠P=∠AOB=60°;
(2)当点P(即P')在劣弧上时,∠AP'B=180°-×120°=120°.
综上所述,∠APB的度数为60°或120°.
[变式] 答案 (0,12)或(0,-12)
解析 设线段BA的中点为E,∵A(4,0)、B(-6,0),∴AB=10,E(-1,0),分情况求解如下:
(1)如图1所示,过点E在第二象限作EP⊥BA,且EP=AB=5,则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5,以点P为圆心,PA(或PB)长为半径作☉P,与y轴的正半轴交于点C,∵∠BCA为圆周角,∴∠BCA=∠BPA=45°,点C即为所求.过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,在Rt△PFC中,PF=1,PC=5,由勾股定理得CF==7,∴OC=OF+CF=5+7=12,∴点C的坐标为(0,12);
(2)如图2所示,在第三象限可以参照(1)作同样操作,同理求得y轴负半轴上的点C的坐标为(0,-12).
综上所述,点C的坐标为(0,12)或(0,-12).
13.解析 (1)补全图形如图所示:
(2)证明:连结PA,PD,PQ,QD.∵=,∴PA=PQ,∵PN⊥AB于点N,∴∠PNA=∠PND=90°,又∵AN=ND,PN=PN,∴△APN≌△DPN,∴∠PAD=∠PDA,PA=PD.∴PD=PQ,∴∠PQD=∠PDQ.∵四边形APQB是圆内接四边形,∴∠PAD+∠PQB=180°,∴∠PDA+∠PQB=180°,∵∠PDA+∠PDB=180°,∴∠PQB=∠PDB,∴∠BQD=∠BDQ,∴BQ=BD.
素养探究全练
14.解析 (1)证明:如图1,连结BC.∵=,∴∠DCB=∠DBC,∵AB是直径,∴∠ACB=∠BCE=90°,∴∠E+∠DBC=90°,∠ECD+∠DCB=90°,
∴∠E=∠DCE,∴CD=ED.
(2)①证明:∵CF=CH,∴∠CFH=∠CHF,∵∠AFO=∠CFH,∴∠AFO=∠CHF,∵=,∴∠CAD=∠BAD,∴△AFO∽△AHC,∴=,∴=,∴CF·AF=FO·AH.
②如图2,连结OD交BC于G.设OG=x,则DG=2-x.∵=,∴∠COD=∠BOD,∵OC=OB,∴OD⊥BC,CG=BG,在Rt△OCG和Rt△BGD中,22-x2=12-(2-x)2,∴x=,即OG=,∵OA=OB,∴OG是△ABC的中位线,∴OG=AC,∴AC=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
第27章 圆
27.1.3 圆周角
基础过关全练
知识点1 圆周角及其定理与推论
1.(2023河南南阳宛城期中)在☉O中,∠ACB是圆周角的是( )
2.(2023吉林长春第二实验中学月考)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
3.【等角转换法】(2023山西省实验中学月考)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则cos∠ADC的值为( )
A. B. C. D.
4.(2023吉林长春第二实验中学期中)如图,将含30°角的三角板的顶点放在半圆上,这个三角板的两边分别与半圆相交于点A,B,则弦AB所对的圆心角是 °.
5.(2023吉林省实验中学模拟)如图,点A,B,C均在☉O上,若∠A=66°,则∠OCB的度数是 .
(2023山西长治上党期末)如图,AB是☉O的直径,C,D两点在☉O上,∠BCD=45°.
(1)求证:AD=BD;
(2)若∠CDB=30°,BC=3,求☉O的半径.
知识点2 圆的内接四边形
7.【一题多解】(2023四川乐山市中模拟)如图,四边形ABCD内接于☉O,AB是☉O的直径,∠ABD=20°,则∠BCD的度数是 .
8.(2023浙江绍兴嵊州期末)如图,四边形ABCD内接于☉O,分别延长BC,AD,使它们相交于点E,AB=8,且DC=DE.
(1)求证:∠A=∠AEB;
(2)若∠EDC=90°,点C为BE的中点,求☉O的半径.
能力提升全练
9.(2023山东泰安中考,7,★☆☆)如图,AB是☉O的直径,D,C是☉O上的点,∠ADC=115°,则∠BAC的度数是( )
A.25° B.30° C.35° D.40°
10.(2023吉林中考,6,★☆☆)如图,AB,AC是☉O的弦,OB,OC是☉O的半径,点P为OB上任意一点(点P不与点B重合),连结CP.若∠BAC=70°,则∠BPC的度数可能是( )
A.70° B.105° C.125° D.155°
11.(2023内蒙古赤峰中考,10,★★☆)如图,圆内接四边形ABCD中,∠BCD=105°,连结OB,OC,OD,BD,∠BOC=2∠COD,则∠CBD的度数是( )
A.25° B.30°
C.35° D.40°
12.【一题多变·给出圆,研究点在圆上的运动】(2023湖南永州模拟,17,★★☆)如图,☉O上有两定点A、B,点P是☉O上一动点(不与A、B两点重合),若∠OAB=30°,则∠APB的度数是 .
[变式·构造圆,研究点在圆上的运动](2023湖南衡阳船山实验中学模拟,20,★☆☆)在平面直角坐标系中,已知点A(4,0)、B(-6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为 .
13.【新考向·尺规作图】【数学文化】(2023山西临汾侯马模拟,21,★★☆)阅读以下材料,并按要求完成相应的关于圆的任务.
关于圆的引理
在《阿基米德全集》的《引理集》中,记述了古希腊的数学家、物理学家阿基米德提出的六个关于圆的引理,其中第二个引理为:如图,在半圆O中,P是上的任意一点,PN⊥直径AB于点N,D在直径AB上,且AN=ND,在上取一点Q,使=,连结BQ,则BQ=BD.
任务:
(1)尺规作图:请根据材料,在图中补全图形;(保留作图痕迹,标明字母,不写作法)
(2)善思小组的同学尝试证明该引理,请按照下面的证明思路,写出该证明的剩余部分.
证明:连结PA,PD,PQ,QD.
……
素养探究全练
14.【推理能力】(2023湖北天门模拟)如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连结AC并延长,与BD的延长线相交于点E,连结CD.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF·AF=FO·AH;
②若圆的半径为2,BD=1,如图3,求AC的长.
答案全解全析
基础过关全练
1.D 选项A、C中,∠ACB的顶点不在圆上,故不是圆周角;选项B中,∠ACB的两边只有一边与圆相交,故不是圆周角.故选D.
2.B ∵直径所对的圆周角等于直角,∴从选项中,可判断圆弧为半圆的是B.
3.B ∵AB为直径,∴∠ACB=90°,∵点A,B,C,D都在同一个圆上,=,∴∠ADC=∠ABC,在Rt△ABC中,cos∠ABC====cos∠ADC.
方法解读 当与已知角有关的问题不易求解时,可先尝试对图形进行分析,能否通过转化的思想将已知角进行转化,从而实现解决问题的目的.常见的等角转换的方法有:等边对等角;两直线平行,同位角、内错角相等;全等或相似三角形的对应角相等;同(等)角的余角、补角相等;平行四边形的对角相等;在同(等)圆中,同弧或等弧所对的圆周角相等等.
4.60
解析 如图,连结OA,OB,由圆周角定理得∠AOB=2∠ACB,∵∠ACB=30°,∴∠AOB=60°.
5.24°
解析 ∵∠A与∠BOC所对弧相同,∴∠BOC=2∠A=2×66°=132°,∵OB=OC,∴∠OBC=∠OCB,∴∠OCB=×(180°-132°)=24°.
6.解析 (1)证明:∵∠DCB=45°,∴∠DAB=∠DCB=45°,∵AB是☉O的直径,∴∠ADB=90°,∴∠ABD=45°,∴∠DAB=∠ABD,∴AD=BD.
(2)如图,连结AC,∵AB是☉O的直径,∴∠ACB=90°,∵∠CAB=∠CDB=30°,BC=3,∴AB=6,∴☉O的半径为3.
7.110°
解析 (解法1:圆周角定理的推论)∵AB是☉O的直径,∴∠ADB=90°,∴∠ABD+∠A=90°.∵∠ABD=20°,∴∠A=70°.∵四边形ABCD是圆内接四边形,∴∠A+∠BCD=180°,∴∠BCD=110°.
(解法2:等腰三角形的性质)如图,连结OD,∵∠AOD=2∠ABD=40°,OA=OD,∴∠OAD=∠ODA=(180°-∠AOD)=70°.∵四边形ABCD是圆内接四边形,∴∠OAD+∠BCD=180°,∴∠BCD=110°.
(解法3:圆周角定理)如图,连结AC,∵AB是☉O的直径,∴∠ACB=90°.∵=,∴∠ACD=∠ABD=20°,∴∠BCD=∠ACD+∠ACB=20°+90°=110°.
8.解析 (1)证明:∵四边形ABCD内接于☉O,∴∠A+∠BCD=180°,∵∠BCD+∠DCE=180°,∴∠A=∠DCE,∵DC=DE,∴∠E=∠DCE,∴∠A=∠AEB.
(2)如图,连结AC,∵∠EDC=90°,∴∠ADC=90°,∴AC是☉O的直径,∴∠ABC=90°,∵∠BAE=∠AEB,∴AB=BE,∵AB=8,∴BE=8,∵点C为BE的中点,∴BC=BE=4,在Rt△ABC中,AC===4,∴☉O的半径为2.
能力提升全练
9.A 如图,连结OC,∵∠ADC=115°,∴优弧所对的圆心角为2×115°=230°,∴∠BOC=230°-180°=50°,∴∠BAC=∠BOC=25°.
10.D ∵∠BAC=70°,∴∠BOC=2∠BAC=140°,∴∠BPC=∠BOC+∠OCP=140°+
∠OCP≥140°.故选D.
11.A ∵四边形ABCD是☉O的内接四边形,∴∠A+∠BCD=180°,∵∠BCD=105°,∴∠A=75°,∴∠BOD=2∠A=150°,∵∠BOC=2∠COD,∴∠BOD=3∠COD=150°,∴∠COD=50°,
∴∠CBD=∠COD=25°.
12.60°或120°
解析 如图,连结OB.∵OA=OB,∴∠OAB=∠OBA=30°,∴∠AOB=120°,分两种情况求解如下:
(1)当点P在优弧上时,∠P=∠AOB=60°;
(2)当点P(即P')在劣弧上时,∠AP'B=180°-×120°=120°.
综上所述,∠APB的度数为60°或120°.
[变式] 答案 (0,12)或(0,-12)
解析 设线段BA的中点为E,∵A(4,0)、B(-6,0),∴AB=10,E(-1,0),分情况求解如下:
(1)如图1所示,过点E在第二象限作EP⊥BA,且EP=AB=5,则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5,以点P为圆心,PA(或PB)长为半径作☉P,与y轴的正半轴交于点C,∵∠BCA为圆周角,∴∠BCA=∠BPA=45°,点C即为所求.过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,在Rt△PFC中,PF=1,PC=5,由勾股定理得CF==7,∴OC=OF+CF=5+7=12,∴点C的坐标为(0,12);
(2)如图2所示,在第三象限可以参照(1)作同样操作,同理求得y轴负半轴上的点C的坐标为(0,-12).
综上所述,点C的坐标为(0,12)或(0,-12).
13.解析 (1)补全图形如图所示:
(2)证明:连结PA,PD,PQ,QD.∵=,∴PA=PQ,∵PN⊥AB于点N,∴∠PNA=∠PND=90°,又∵AN=ND,PN=PN,∴△APN≌△DPN,∴∠PAD=∠PDA,PA=PD.∴PD=PQ,∴∠PQD=∠PDQ.∵四边形APQB是圆内接四边形,∴∠PAD+∠PQB=180°,∴∠PDA+∠PQB=180°,∵∠PDA+∠PDB=180°,∴∠PQB=∠PDB,∴∠BQD=∠BDQ,∴BQ=BD.
素养探究全练
14.解析 (1)证明:如图1,连结BC.∵=,∴∠DCB=∠DBC,∵AB是直径,∴∠ACB=∠BCE=90°,∴∠E+∠DBC=90°,∠ECD+∠DCB=90°,
∴∠E=∠DCE,∴CD=ED.
(2)①证明:∵CF=CH,∴∠CFH=∠CHF,∵∠AFO=∠CFH,∴∠AFO=∠CHF,∵=,∴∠CAD=∠BAD,∴△AFO∽△AHC,∴=,∴=,∴CF·AF=FO·AH.
②如图2,连结OD交BC于G.设OG=x,则DG=2-x.∵=,∴∠COD=∠BOD,∵OC=OB,∴OD⊥BC,CG=BG,在Rt△OCG和Rt△BGD中,22-x2=12-(2-x)2,∴x=,即OG=,∵OA=OB,∴OG是△ABC的中位线,∴OG=AC,∴AC=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
