2024华东师大版数学九年级下学期课时练--27.3.1 弧长和扇形的面积(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--27.3.1 弧长和扇形的面积(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 616.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 20:30:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
第27章 圆
27.3 圆中的计算问题
27.3.1 弧长和扇形的面积
基础过关全练
知识点1 弧长公式
1.【一题多变·已知圆心角度数和半径长,求弧长】
(2023四川成都武侯期末)一个扇形的半径是4 cm,圆心角是45°,则此扇形的弧长是( )
A.π cm B.2π cm C.4π cm D.8π cm
[变式·已知弧长和半径长,求圆心角度数](2023浙江金华婺城模拟)如果一个扇形的半径是2,弧长是,则此扇形的圆心角的度数为( )
A.30° B.45° C.60° D.90°
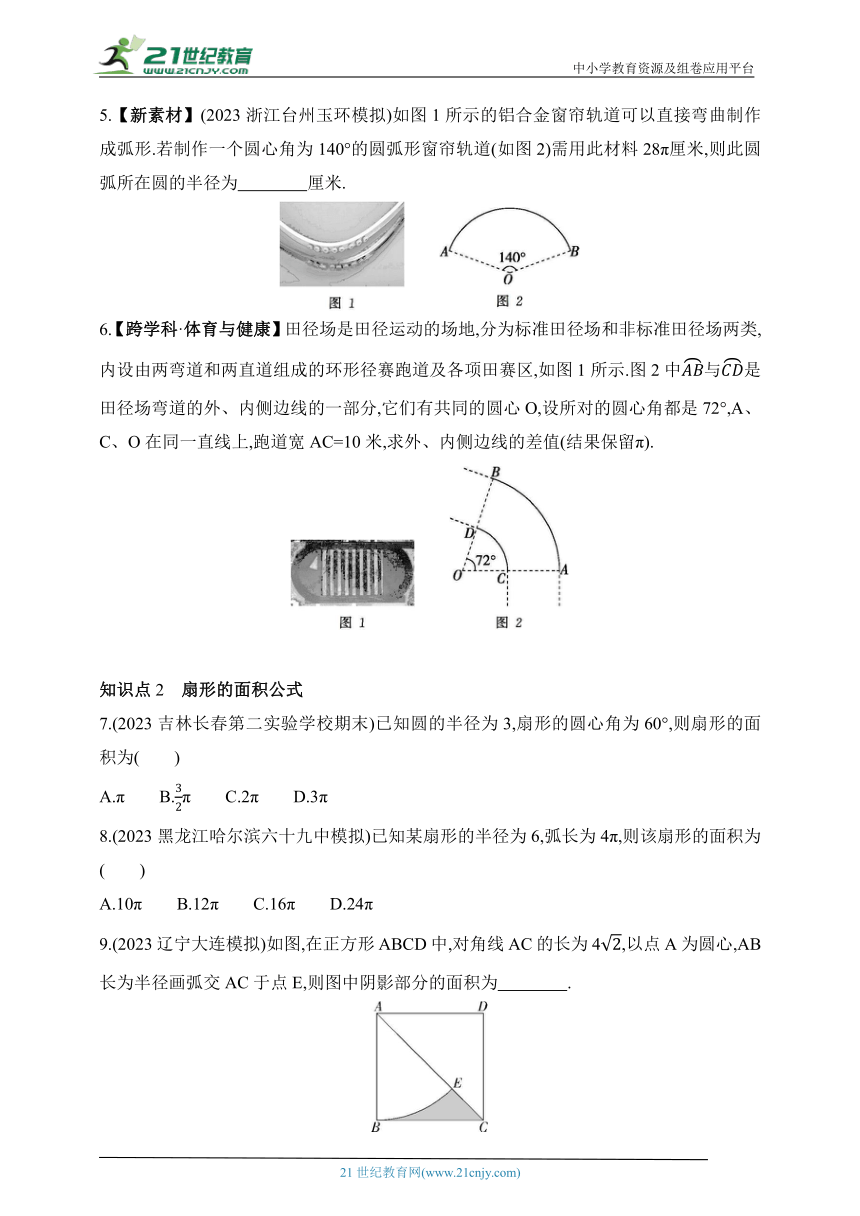
2.(2023四川资阳模拟)如图,☉A的圆心A关于弦CD的对称点为B,且☉A的半径为3,则劣弧BD的长是( )
A. B.π C. D.
3.(2023山东威海模拟)如图所示的正方形网格中,O,A,B,C,D是网格线交点,若弧CD与弧AB所在圆的圆心都为点O,则弧CD与弧AB的长度之比为 .
4.【跨学科·物理】【中华优秀传统文化】(2023陕西西安碑林西北工大附中模拟)《墨经》是中国古籍中最早讨论滑轮力学的著作.如图所示的是书中记载的一个滑轮机械,称为“绳制”.若图中的定滑轮半径为6 cm,滑轮旋转了15°,则重物“甲”上升了 cm.(绳索粗细不计,且与滑轮之间无滑动,结果保留π)
5.【新素材】(2023浙江台州玉环模拟)如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形.若制作一个圆心角为140°的圆弧形窗帘轨道(如图2)需用此材料28π厘米,则此圆弧所在圆的半径为 厘米.
6.【跨学科·体育与健康】田径场是田径运动的场地,分为标准田径场和非标准田径场两类,内设由两弯道和两直道组成的环形径赛跑道及各项田赛区,如图1所示.图2中与是田径场弯道的外、内侧边线的一部分,它们有共同的圆心O,设所对的圆心角都是72°,A、C、O在同一直线上,跑道宽AC=10米,求外、内侧边线的差值(结果保留π).
知识点2 扇形的面积公式
7.(2023吉林长春第二实验学校期末)已知圆的半径为3,扇形的圆心角为60°,则扇形的面积为( )
A.π B.π C.2π D.3π
8.(2023黑龙江哈尔滨六十九中模拟)已知某扇形的半径为6,弧长为4π,则该扇形的面积为( )
A.10π B.12π C.16π D.24π
9.(2023辽宁大连模拟)如图,在正方形ABCD中,对角线AC的长为4,以点A为圆心,AB长为半径画弧交AC于点E,则图中阴影部分的面积为 .
10.【等积变换求面积】(2023内蒙古包头中考)如图,正方形ABCD的边长为2,对角线AC,BD相交于点O,以点B为圆心,对角线BD的长为半径画弧,交BC的延长线于点E,则图中阴影部分的面积为 .
11.(2023吉林长春第二实验学校模拟)如图,Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,以A为圆心,AC长为半径画弧,交AB于点E,以B为圆心,BC长为半径画弧,交AB于点D,则图中阴影部分的面积为 (结果保留π).
12.(2023贵州铜仁玉屏模拟)如图,已知AB是☉O的直径,点C,D在☉O上,∠D=60°且AB=6,过点O作OE⊥AC交☉O于点F,垂足为E.
(1)∠CAB的度数为 ;
(2)求OE的长;
(3)求阴影部分的面积.
能力提升全练
13.(2023甘肃兰州中考,6,★☆☆)如图1所示的是一段弯管,弯管的部分外轮廓线如图2所示,是一条圆弧AB,圆弧的半径OA=20 cm,圆心角∠AOB=90°,则的长=( )
A.20π cm B.10π cm C.5π cm D.2π cm
14.(2023江苏南通启东模拟,7,★☆☆)如图,四边形ABCD是☉O的内接四边形,连结AC,AC=AD,若∠ABC=130°,☉O的半径为9,则劣弧的长为( )
A.4π B.8π C.9π D.18π
15.(2022山西太原二模,10,★★☆)如图所示的是一张圆心为O,半径为4 cm的圆形纸片,沿弦AC所在直线折叠,使得经过点O,将纸片☉O展开后,折痕为AC,作半径OB⊥OA,则图中阴影部分的面积等于( )
A.(4π-4)cm2 B.π cm2
C.cm2 D.cm2
16.(2023吉林中考,13,★☆☆)如图1,A,B表示某游乐场摩天轮上的两个轿厢.图2是其示意图,点O是圆心,半径r为15 m,点A,B是圆上的两点,圆心角∠AOB=120°,则的长为 m.(结果保留π)
17.【中华优秀传统文化】(2023四川成都中考,21,★★☆)为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出.该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳 名观众同时观看演出.(π≈3.14,≈1.73)
18.(2022河南中考,14,★★☆)如图,将扇形AOB沿OB方向平移,使点O移到OB的中点O'处,得到扇形A'O'B'.若∠O=90°,OA=2,则阴影部分的面积为 .
19.(2023黑龙江齐齐哈尔中考,21,★☆☆)如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E是斜边AC上一点,以AE为直径的☉O经过点D,交AB于点F,连结DF.
(1)求证:BC是☉O的切线;
(2)若BD=5,tan∠ADB=,求图中阴影部分的面积.(结果保留π)
20.【跨学科·物理】(2023湖南衡阳石鼓模拟,26,★★☆)粒子加速器是当今高能物理学中研究有关宇宙的基本问题的重要工具,图1、图2是我国某环形粒子加速器的实景图和构造原理图,图3是粒子加速器的俯视示意图,其中粒子真空室可看作☉O,粒子在A点注入,经过优弧后,在B点引出,粒子注入和引出的路径都与☉O相切,C,D是两个加速电极,粒子在经过时被加速.已知AB=16 km,粒子注入路径与AB的夹角α=53°,所对的圆心角是90°.tan 37°≈,π≈3.14
(1)求☉O的直径;
(2)与AB的长度哪个更长
素养探究全练
21【推理能力】(2022河南漯河舞阳期末)如图,有一个直径MN=4的半圆形纸片,其圆心为点P,从初始阶段位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中位置Ⅰ中的MN平行于数轴,且半圆P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中的点N到数轴的距离为3,且半圆P与数轴相切于点A.解答下列问题:
(1)位置Ⅰ中的MN与数轴之间的距离为 ;位置Ⅱ中的半圆P与数轴的位置关系是 ;
(2)求位置Ⅲ中的圆心P在数轴上表示的数;
(3)纸片半圆P从位置Ⅲ翻滚到位置Ⅳ时,求点N所经过的路径长及该纸片所扫过的图形的面积;
(4)求OA的长.(结果保留π)
答案全解全析
基础过关全练
1.A 由题意得此扇形的弧长为=π(cm).
[变式] B 设此扇形的圆心角度数为n,∵扇形的弧长为,半径为2,∴=,解得n=45°.
2.B 如图,连结AD、AB,AB与CD的交点为E,∵A、B关于弦CD对称,∴CD垂直平分AB,∵AD=AB,∴AE=AD,∴∠ADE=30°,∴∠BAD=60°,∴劣弧BD的长为=π.
3.∶1
解析 设题图中小正方形的边长均为1,则CD=4,由勾股定理得OC=OD==2,则OC2+OD2=CD2,∴∠COD=90°,∴与的长度之比=∶=∶1.
4.π
解析 由题意得重物上升的距离是半径为6 cm,圆心角为15°的扇形的弧长,即=π(cm).
5.36
解析 设此圆弧所在圆的半径为R厘米,由弧长公式得=28π,解得R=36,即此圆弧所在圆的半径为36厘米.
6.解析 的长==4π-,的长=,故外、内侧边线的差值为4π--=4π(米).
7.B ∵圆的半径为3,扇形的圆心角为60°,∴S扇形==π.
8.B S扇形=lR=×4π×6=12π.
9.8-2π
解析 ∵四边形ABCD是正方形,∴∠BAC=45°,∠ABC=90°,AB=BC,∵AC=4,∴AB=BC=4,∴S阴影=S△ABC-=×4×4-=8-2π.
10.π
解析 ∵四边形ABCD是正方形,∴AO=CO,BO=DO,AD=BC=CD,∠DBE=45°,∴△AOD≌△COB,∵正方形ABCD的边长为2,∴BD==2,∴阴影部分的面积为扇形BED的面积,即=π.
方法解读 当所求阴影部分的面积无法直接求或求解比较麻烦时,可用平移、旋转、轴对称等变换,将阴影部分进行转移、重组,转化成规则图形后进行求解.
11.π-8
解析 Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,∴∠B=30°,BC=AC=4,∴阴影部分的面积=+-S△ACB=+-×4×4=π-8.
12.解析 (1)∵AB是☉O的直径,∴∠ACB=90°,∵∠B=∠D=60°,∴∠CAB=90°-∠B=30°.
(2)∵AB=6,∴OA=AB=3,∵OF⊥AC,∴∠AEO=90°,∵∠BAC=30°,∴OE=OA=1.5.
(3)如图,连结OC.∵∠AEO=90°,∠CAB=30°,∴∠AOE=60°,∵OF=OA,∴△OAF是等边三角形,∴OE=EF,∵∠CEO=∠AEF=90°,AE=CE,∴△OEC≌△FEA,∴S阴影=,∵∠B=60°,OC=OB,∴△OBC是等边三角形,∴∠BOC=60°,∴∠COF=180°-∠AOF-∠BOC=60°,∴扇形OCF的面积==,∴阴影的面积=.
能力提升全练
13.B 的长==10π(cm).
14.B 如图,连结OD,OC,∵四边形ABCD是☉O的内接四边形,∴∠ABC+∠ADC=180°,∵∠ABC=130°,∴∠ADC=50°,∵AC=AD,
∴∠ACD=∠ADC=50°,∴∠DAC=80°,∴∠DOC=2∠DAC=160°,∴的长==8π.
15.D 如图,作OD⊥AC于H,交于点D,连结OC,∴∠AHO=90°.由折叠可知S弓形ABC=S弓形AOC,HO=HD=OD=2,∠AHO=∠AHD=90°,在Rt△AOH中,由勾股定理得AH==2.∵cos∠AOH==,∴∠AOH=60°.∵AO=CO,OD⊥AC,∴∠AOC=2∠AOH=120°,AC=2AH=4,∴S弓形ABC=S扇形OAC-S△OAC=-×4×2=-4,∴S阴影=2S弓形ABC-S扇形OAB=2-=cm2.
16.10π
解析 ∵∠AOB=120°,☉O的半径r为15 m,∴的长==10π(m).
17.184
解析 如图,过O作OD⊥AB,D为垂足,∴AD=BD,OD=5米,∵cos∠AOD===,∴∠AOD=60°,∴AD=OD=5米,∠AOB=120°,∴AB=10米,∴S阴影=-S△OAB=-×10×5=π-25≈61.4(平方米),∴61.4×3≈184(名),∴最多可容纳184名观众同时观看演出.
18.+
解析 如图,设O'A'交于点T,连结OT.∵OT=OB,OO'=O'B,∴OT=2OO',∵∠OO'T=90°,∴∠O'TO=30°,∠TOO'=60°,易知OO'=1,∴O'T=,∴S阴影=S扇形O'A'B'-(S扇形OTB-S△OTO')=-=+.
19.解析 (1)证明:如图,连结OD,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠BAD,∴∠ODA=∠BAD,∴OD∥AB,∴∠ODC=∠B=90°,∵OD是☉O的半径,∴BC是☉O的切线.
(2)如图,连结OF,DE,∵∠B=90°,tan∠ADB=,∴∠ADB=60°,∠BAD=30°,∵BD=5,
∴AD=2BD=10,∵AE是☉O的直径,∴∠ADE=90°,∵AD平分∠BAC,∴∠DAE=∠BAD=30°,在Rt△ADE中,AD=10,∵cos∠DAE==,∴AE=,∴OA=AE=,
∵∠BAC=60°,OA=OF,∴△AOF是等边三角形,∴∠AOF=60°,∵OD∥AB,∴S△ADF=S△AOF,∴S阴影===.
20.解析 (1)如图,过点O作OE⊥AB于点E,连结AO,∵AF是☉O的切线,∴∠FAO=90°,∵α=53°,∴∠EAO=90°-53°=37°,
∵OE⊥AB,AB=16 km,∴AE=BE=AB=×16=8(km),∠AEO=90°,
∴tan∠EAO==tan37°≈,∴OE≈AE=×8=6(km),
∴AO==10(km),
∴☉O的直径约为2AO=20 km.
(2)AB的长度更长一些.理由如下:∵所对的圆心角为90°,OC=OA=10 km,∴的长度为≈15.7(km),
∵15.7<16,∴AB的长度更长一些.
素养探究全练
21.解析 (1)∵半圆P的直径MN=4,∴半圆P的半径=2,∵此时的半圆P与数轴相切,且MN平行于数轴,∴位置Ⅰ中的MN与数轴之间的距离为2.位置Ⅱ中的半圆P与数轴的位置关系是相切.
(2)位置Ⅲ中数轴上线段ON的长与位置Ⅰ中的长相等,∵的长为=π,NP=2,∴位置Ⅲ中的圆心P在数轴上表示的数为ON+NP=π+2.
(3)点N所经过的路径长为=2π,纸片所扫过的图形的面积为+=2π+4π=6π.
(4)如图,作NC垂直数轴于点C,作PH⊥NC于点H,连结PA,则四边形PHCA为矩形.在Rt△NPH中,PN=2,NH=NC-HC=NC-PA=1,∴sin∠NPH==,∴∠NPH=30°,∴∠MPA=60°,∴的长为=,∴OA的长为π+4+π=π+4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
第27章 圆
27.3 圆中的计算问题
27.3.1 弧长和扇形的面积
基础过关全练
知识点1 弧长公式
1.【一题多变·已知圆心角度数和半径长,求弧长】
(2023四川成都武侯期末)一个扇形的半径是4 cm,圆心角是45°,则此扇形的弧长是( )
A.π cm B.2π cm C.4π cm D.8π cm
[变式·已知弧长和半径长,求圆心角度数](2023浙江金华婺城模拟)如果一个扇形的半径是2,弧长是,则此扇形的圆心角的度数为( )
A.30° B.45° C.60° D.90°
2.(2023四川资阳模拟)如图,☉A的圆心A关于弦CD的对称点为B,且☉A的半径为3,则劣弧BD的长是( )
A. B.π C. D.
3.(2023山东威海模拟)如图所示的正方形网格中,O,A,B,C,D是网格线交点,若弧CD与弧AB所在圆的圆心都为点O,则弧CD与弧AB的长度之比为 .
4.【跨学科·物理】【中华优秀传统文化】(2023陕西西安碑林西北工大附中模拟)《墨经》是中国古籍中最早讨论滑轮力学的著作.如图所示的是书中记载的一个滑轮机械,称为“绳制”.若图中的定滑轮半径为6 cm,滑轮旋转了15°,则重物“甲”上升了 cm.(绳索粗细不计,且与滑轮之间无滑动,结果保留π)
5.【新素材】(2023浙江台州玉环模拟)如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形.若制作一个圆心角为140°的圆弧形窗帘轨道(如图2)需用此材料28π厘米,则此圆弧所在圆的半径为 厘米.
6.【跨学科·体育与健康】田径场是田径运动的场地,分为标准田径场和非标准田径场两类,内设由两弯道和两直道组成的环形径赛跑道及各项田赛区,如图1所示.图2中与是田径场弯道的外、内侧边线的一部分,它们有共同的圆心O,设所对的圆心角都是72°,A、C、O在同一直线上,跑道宽AC=10米,求外、内侧边线的差值(结果保留π).
知识点2 扇形的面积公式
7.(2023吉林长春第二实验学校期末)已知圆的半径为3,扇形的圆心角为60°,则扇形的面积为( )
A.π B.π C.2π D.3π
8.(2023黑龙江哈尔滨六十九中模拟)已知某扇形的半径为6,弧长为4π,则该扇形的面积为( )
A.10π B.12π C.16π D.24π
9.(2023辽宁大连模拟)如图,在正方形ABCD中,对角线AC的长为4,以点A为圆心,AB长为半径画弧交AC于点E,则图中阴影部分的面积为 .
10.【等积变换求面积】(2023内蒙古包头中考)如图,正方形ABCD的边长为2,对角线AC,BD相交于点O,以点B为圆心,对角线BD的长为半径画弧,交BC的延长线于点E,则图中阴影部分的面积为 .
11.(2023吉林长春第二实验学校模拟)如图,Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,以A为圆心,AC长为半径画弧,交AB于点E,以B为圆心,BC长为半径画弧,交AB于点D,则图中阴影部分的面积为 (结果保留π).
12.(2023贵州铜仁玉屏模拟)如图,已知AB是☉O的直径,点C,D在☉O上,∠D=60°且AB=6,过点O作OE⊥AC交☉O于点F,垂足为E.
(1)∠CAB的度数为 ;
(2)求OE的长;
(3)求阴影部分的面积.
能力提升全练
13.(2023甘肃兰州中考,6,★☆☆)如图1所示的是一段弯管,弯管的部分外轮廓线如图2所示,是一条圆弧AB,圆弧的半径OA=20 cm,圆心角∠AOB=90°,则的长=( )
A.20π cm B.10π cm C.5π cm D.2π cm
14.(2023江苏南通启东模拟,7,★☆☆)如图,四边形ABCD是☉O的内接四边形,连结AC,AC=AD,若∠ABC=130°,☉O的半径为9,则劣弧的长为( )
A.4π B.8π C.9π D.18π
15.(2022山西太原二模,10,★★☆)如图所示的是一张圆心为O,半径为4 cm的圆形纸片,沿弦AC所在直线折叠,使得经过点O,将纸片☉O展开后,折痕为AC,作半径OB⊥OA,则图中阴影部分的面积等于( )
A.(4π-4)cm2 B.π cm2
C.cm2 D.cm2
16.(2023吉林中考,13,★☆☆)如图1,A,B表示某游乐场摩天轮上的两个轿厢.图2是其示意图,点O是圆心,半径r为15 m,点A,B是圆上的两点,圆心角∠AOB=120°,则的长为 m.(结果保留π)
17.【中华优秀传统文化】(2023四川成都中考,21,★★☆)为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出.该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳 名观众同时观看演出.(π≈3.14,≈1.73)
18.(2022河南中考,14,★★☆)如图,将扇形AOB沿OB方向平移,使点O移到OB的中点O'处,得到扇形A'O'B'.若∠O=90°,OA=2,则阴影部分的面积为 .
19.(2023黑龙江齐齐哈尔中考,21,★☆☆)如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E是斜边AC上一点,以AE为直径的☉O经过点D,交AB于点F,连结DF.
(1)求证:BC是☉O的切线;
(2)若BD=5,tan∠ADB=,求图中阴影部分的面积.(结果保留π)
20.【跨学科·物理】(2023湖南衡阳石鼓模拟,26,★★☆)粒子加速器是当今高能物理学中研究有关宇宙的基本问题的重要工具,图1、图2是我国某环形粒子加速器的实景图和构造原理图,图3是粒子加速器的俯视示意图,其中粒子真空室可看作☉O,粒子在A点注入,经过优弧后,在B点引出,粒子注入和引出的路径都与☉O相切,C,D是两个加速电极,粒子在经过时被加速.已知AB=16 km,粒子注入路径与AB的夹角α=53°,所对的圆心角是90°.tan 37°≈,π≈3.14
(1)求☉O的直径;
(2)与AB的长度哪个更长
素养探究全练
21【推理能力】(2022河南漯河舞阳期末)如图,有一个直径MN=4的半圆形纸片,其圆心为点P,从初始阶段位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中位置Ⅰ中的MN平行于数轴,且半圆P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中的点N到数轴的距离为3,且半圆P与数轴相切于点A.解答下列问题:
(1)位置Ⅰ中的MN与数轴之间的距离为 ;位置Ⅱ中的半圆P与数轴的位置关系是 ;
(2)求位置Ⅲ中的圆心P在数轴上表示的数;
(3)纸片半圆P从位置Ⅲ翻滚到位置Ⅳ时,求点N所经过的路径长及该纸片所扫过的图形的面积;
(4)求OA的长.(结果保留π)
答案全解全析
基础过关全练
1.A 由题意得此扇形的弧长为=π(cm).
[变式] B 设此扇形的圆心角度数为n,∵扇形的弧长为,半径为2,∴=,解得n=45°.
2.B 如图,连结AD、AB,AB与CD的交点为E,∵A、B关于弦CD对称,∴CD垂直平分AB,∵AD=AB,∴AE=AD,∴∠ADE=30°,∴∠BAD=60°,∴劣弧BD的长为=π.
3.∶1
解析 设题图中小正方形的边长均为1,则CD=4,由勾股定理得OC=OD==2,则OC2+OD2=CD2,∴∠COD=90°,∴与的长度之比=∶=∶1.
4.π
解析 由题意得重物上升的距离是半径为6 cm,圆心角为15°的扇形的弧长,即=π(cm).
5.36
解析 设此圆弧所在圆的半径为R厘米,由弧长公式得=28π,解得R=36,即此圆弧所在圆的半径为36厘米.
6.解析 的长==4π-,的长=,故外、内侧边线的差值为4π--=4π(米).
7.B ∵圆的半径为3,扇形的圆心角为60°,∴S扇形==π.
8.B S扇形=lR=×4π×6=12π.
9.8-2π
解析 ∵四边形ABCD是正方形,∴∠BAC=45°,∠ABC=90°,AB=BC,∵AC=4,∴AB=BC=4,∴S阴影=S△ABC-=×4×4-=8-2π.
10.π
解析 ∵四边形ABCD是正方形,∴AO=CO,BO=DO,AD=BC=CD,∠DBE=45°,∴△AOD≌△COB,∵正方形ABCD的边长为2,∴BD==2,∴阴影部分的面积为扇形BED的面积,即=π.
方法解读 当所求阴影部分的面积无法直接求或求解比较麻烦时,可用平移、旋转、轴对称等变换,将阴影部分进行转移、重组,转化成规则图形后进行求解.
11.π-8
解析 Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=4,∴∠B=30°,BC=AC=4,∴阴影部分的面积=+-S△ACB=+-×4×4=π-8.
12.解析 (1)∵AB是☉O的直径,∴∠ACB=90°,∵∠B=∠D=60°,∴∠CAB=90°-∠B=30°.
(2)∵AB=6,∴OA=AB=3,∵OF⊥AC,∴∠AEO=90°,∵∠BAC=30°,∴OE=OA=1.5.
(3)如图,连结OC.∵∠AEO=90°,∠CAB=30°,∴∠AOE=60°,∵OF=OA,∴△OAF是等边三角形,∴OE=EF,∵∠CEO=∠AEF=90°,AE=CE,∴△OEC≌△FEA,∴S阴影=,∵∠B=60°,OC=OB,∴△OBC是等边三角形,∴∠BOC=60°,∴∠COF=180°-∠AOF-∠BOC=60°,∴扇形OCF的面积==,∴阴影的面积=.
能力提升全练
13.B 的长==10π(cm).
14.B 如图,连结OD,OC,∵四边形ABCD是☉O的内接四边形,∴∠ABC+∠ADC=180°,∵∠ABC=130°,∴∠ADC=50°,∵AC=AD,
∴∠ACD=∠ADC=50°,∴∠DAC=80°,∴∠DOC=2∠DAC=160°,∴的长==8π.
15.D 如图,作OD⊥AC于H,交于点D,连结OC,∴∠AHO=90°.由折叠可知S弓形ABC=S弓形AOC,HO=HD=OD=2,∠AHO=∠AHD=90°,在Rt△AOH中,由勾股定理得AH==2.∵cos∠AOH==,∴∠AOH=60°.∵AO=CO,OD⊥AC,∴∠AOC=2∠AOH=120°,AC=2AH=4,∴S弓形ABC=S扇形OAC-S△OAC=-×4×2=-4,∴S阴影=2S弓形ABC-S扇形OAB=2-=cm2.
16.10π
解析 ∵∠AOB=120°,☉O的半径r为15 m,∴的长==10π(m).
17.184
解析 如图,过O作OD⊥AB,D为垂足,∴AD=BD,OD=5米,∵cos∠AOD===,∴∠AOD=60°,∴AD=OD=5米,∠AOB=120°,∴AB=10米,∴S阴影=-S△OAB=-×10×5=π-25≈61.4(平方米),∴61.4×3≈184(名),∴最多可容纳184名观众同时观看演出.
18.+
解析 如图,设O'A'交于点T,连结OT.∵OT=OB,OO'=O'B,∴OT=2OO',∵∠OO'T=90°,∴∠O'TO=30°,∠TOO'=60°,易知OO'=1,∴O'T=,∴S阴影=S扇形O'A'B'-(S扇形OTB-S△OTO')=-=+.
19.解析 (1)证明:如图,连结OD,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠BAD,∴∠ODA=∠BAD,∴OD∥AB,∴∠ODC=∠B=90°,∵OD是☉O的半径,∴BC是☉O的切线.
(2)如图,连结OF,DE,∵∠B=90°,tan∠ADB=,∴∠ADB=60°,∠BAD=30°,∵BD=5,
∴AD=2BD=10,∵AE是☉O的直径,∴∠ADE=90°,∵AD平分∠BAC,∴∠DAE=∠BAD=30°,在Rt△ADE中,AD=10,∵cos∠DAE==,∴AE=,∴OA=AE=,
∵∠BAC=60°,OA=OF,∴△AOF是等边三角形,∴∠AOF=60°,∵OD∥AB,∴S△ADF=S△AOF,∴S阴影===.
20.解析 (1)如图,过点O作OE⊥AB于点E,连结AO,∵AF是☉O的切线,∴∠FAO=90°,∵α=53°,∴∠EAO=90°-53°=37°,
∵OE⊥AB,AB=16 km,∴AE=BE=AB=×16=8(km),∠AEO=90°,
∴tan∠EAO==tan37°≈,∴OE≈AE=×8=6(km),
∴AO==10(km),
∴☉O的直径约为2AO=20 km.
(2)AB的长度更长一些.理由如下:∵所对的圆心角为90°,OC=OA=10 km,∴的长度为≈15.7(km),
∵15.7<16,∴AB的长度更长一些.
素养探究全练
21.解析 (1)∵半圆P的直径MN=4,∴半圆P的半径=2,∵此时的半圆P与数轴相切,且MN平行于数轴,∴位置Ⅰ中的MN与数轴之间的距离为2.位置Ⅱ中的半圆P与数轴的位置关系是相切.
(2)位置Ⅲ中数轴上线段ON的长与位置Ⅰ中的长相等,∵的长为=π,NP=2,∴位置Ⅲ中的圆心P在数轴上表示的数为ON+NP=π+2.
(3)点N所经过的路径长为=2π,纸片所扫过的图形的面积为+=2π+4π=6π.
(4)如图,作NC垂直数轴于点C,作PH⊥NC于点H,连结PA,则四边形PHCA为矩形.在Rt△NPH中,PN=2,NH=NC-HC=NC-PA=1,∴sin∠NPH==,∴∠NPH=30°,∴∠MPA=60°,∴的长为=,∴OA的长为π+4+π=π+4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
