2024华东师大版数学九年级下学期课时练--27.4 正多边形和圆(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--27.4 正多边形和圆(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 604.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
第27章 圆
27.4 正多边形和圆
基础过关全练
知识点1 圆内接正多边形及相关定义
1.【易错题】(2022吉林长春宽城期末)给出下列说法:①各边相等的圆内接多边形是正多边形;②各边相等的圆外切多边形是正多边形;③各角相等的圆内接多边形是正多边形;④各角相等的圆外切多边形是正多边形.其中正确的是( )
A.①④ B.②③
C.①③ D.②④
2.(2022广东潮州饶平英才实验中学月考)如图所示,△OAB为正三角形,以点O为圆心,OA长为半径作☉O,直径FC∥AB,AO,BO的延长线分别交☉O于点D,E,连结DE、EF、AF、CD、BC.求证:六边形ABCDEF是正六边形.
知识点2 圆内接正多边形的相关计算
3.(2022四川成都中考)如图,正六边形ABCDEF内接于☉O,若☉O的周长等于6π,则正六边形的边长为( )
A. B. C.3 D.2
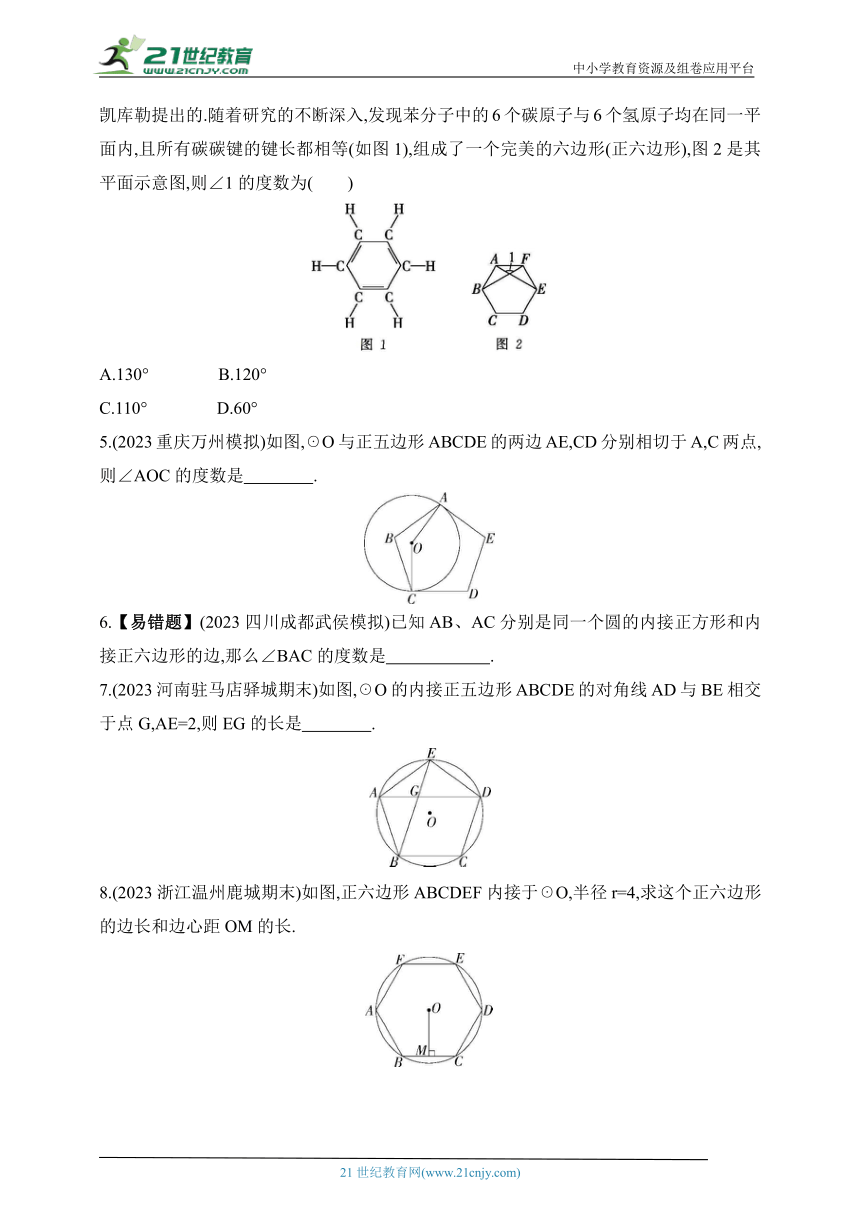
4.【跨学科·化学】(2023湖南衡阳船山实验中学模拟)苯分子的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子与6个氢原子均在同一平面内,且所有碳碳键的键长都相等(如图1),组成了一个完美的六边形(正六边形),图2是其平面示意图,则∠1的度数为( )
A.130° B.120°
C.110° D.60°
5.(2023重庆万州模拟)如图,☉O与正五边形ABCDE的两边AE,CD分别相切于A,C两点,则∠AOC的度数是 .
6.【易错题】(2023四川成都武侯模拟)已知AB、AC分别是同一个圆的内接正方形和内接正六边形的边,那么∠BAC的度数是 .
7.(2023河南驻马店驿城期末)如图,☉O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 .
8.(2023浙江温州鹿城期末)如图,正六边形ABCDEF内接于☉O,半径r=4,求这个正六边形的边长和边心距OM的长.
知识点3 正多边形的画法
9.剪纸艺术是最古老的中国民间艺术之一,山东烟台的剪纸是其中比较有代表性的.传统的剪纸先通过对折的方式将纸等分,小颖想通过将圆形纸片八等分的方式作正多边形,请你帮小颖利用直尺和圆规作一个正八边形.
能力提升全练
10.(2023安徽中考,6,★☆☆)如图,正五边形ABCDE内接于☉O,连结OC,OD,则∠BAE-∠COD=( )
A.60° B.54° C.48° D.36°
11.【新素材】(2023山西中考,10,★★☆)蜂巢结构精巧,其巢房横截面的形状均为正六边形.下图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点P,Q,M均为正六边形的顶点.若点P,Q的坐标分别为(-2,3),(0,-3),则点M的坐标为( )
A.(3,-2) B.(3,2)
C.(2,-3) D.(-2,-3)
12.【数学文化】(2023福建中考,10,★☆☆)中国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣.”“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,☉O的半径为1,运用“割圆术”,以圆内接正六边形的面积近似估计☉O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为( )
A. B.2
C.3 D.2
13.【新素材】(2022山西大同新荣模拟,23,★☆☆)阅读与思考
请阅读下列材料,并完成相应的任务:
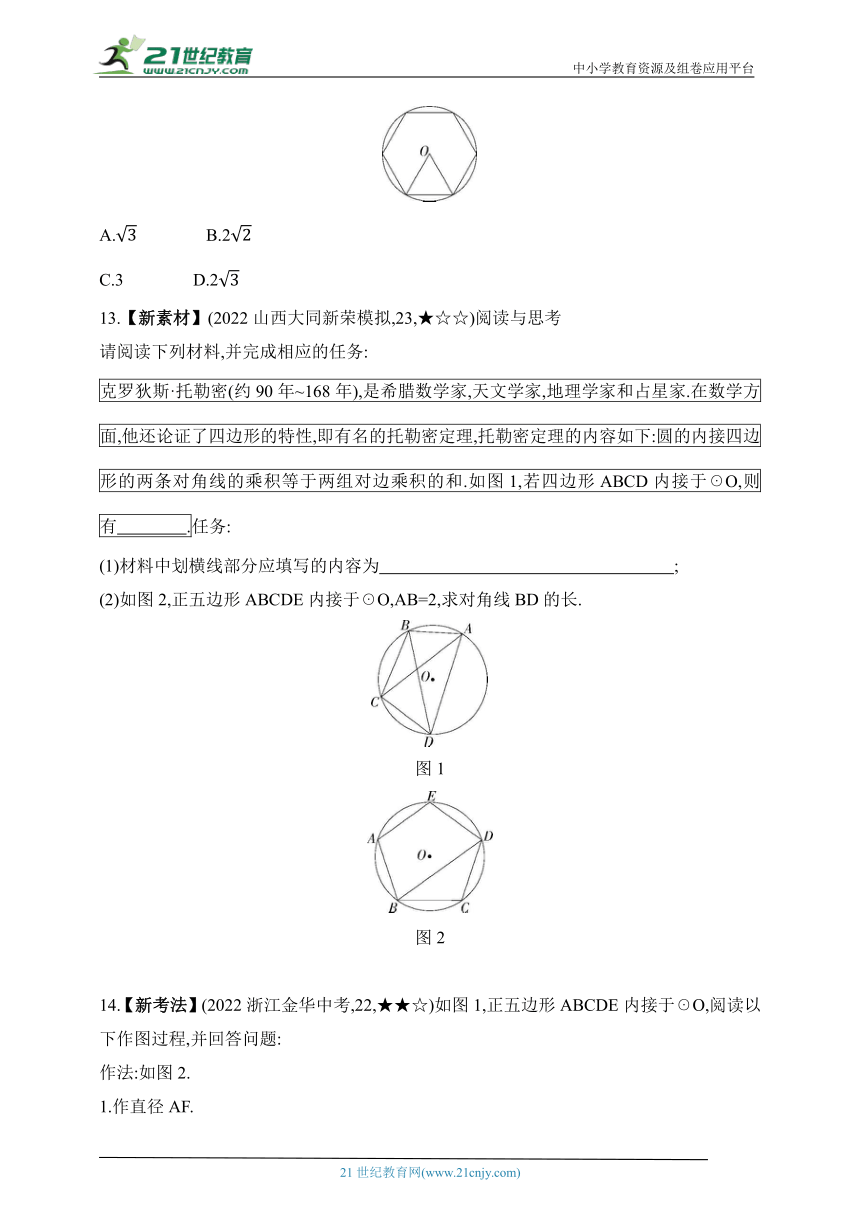
克罗狄斯·托勒密(约90年~168年),是希腊数学家,天文学家,地理学家和占星家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理,托勒密定理的内容如下:圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.如图1,若四边形ABCD内接于☉O,则有 .任务:
(1)材料中划横线部分应填写的内容为 ;
(2)如图2,正五边形ABCDE内接于☉O,AB=2,求对角线BD的长.
图1
图2
14.【新考法】(2022浙江金华中考,22,★★☆)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答问题:
作法:如图2.
1.作直径AF.
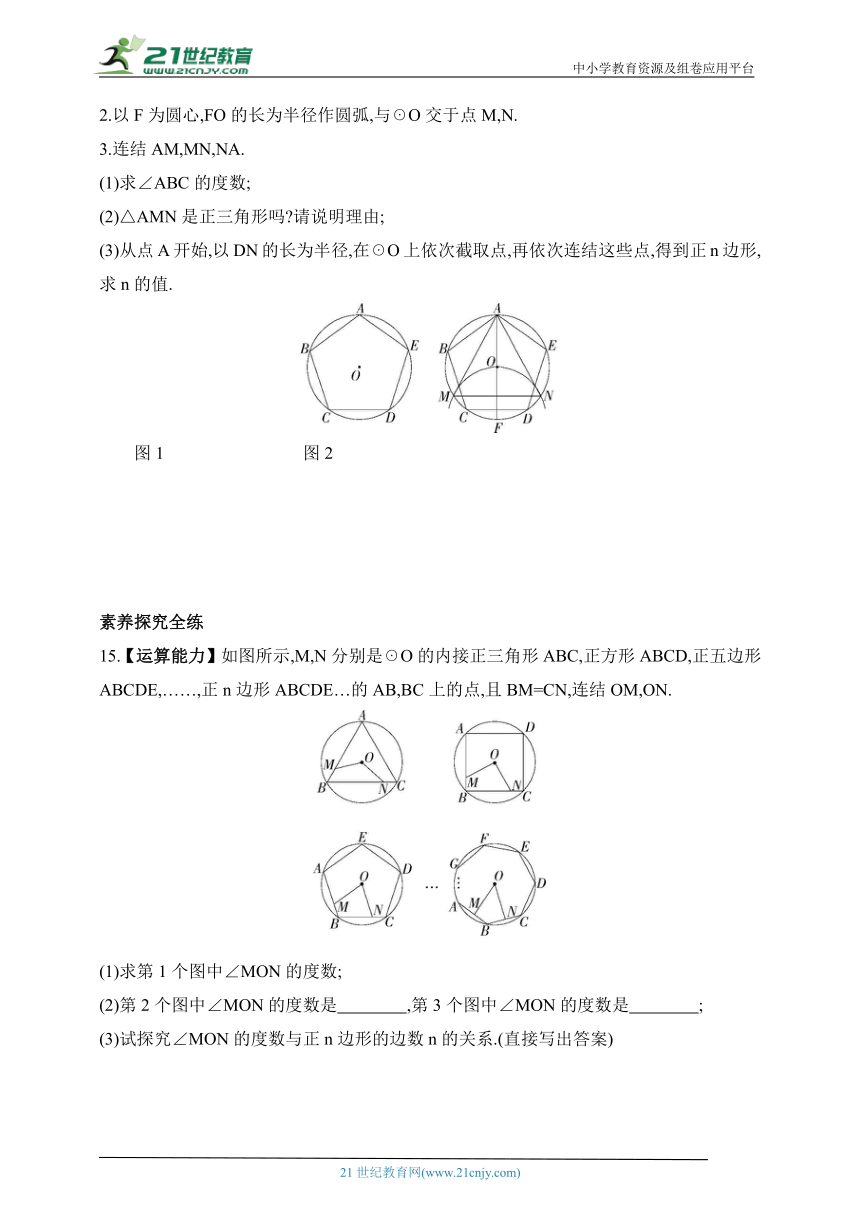
2.以F为圆心,FO的长为半径作圆弧,与☉O交于点M,N.
3.连结AM,MN,NA.
(1)求∠ABC的度数;
(2)△AMN是正三角形吗 请说明理由;
(3)从点A开始,以DN的长为半径,在☉O上依次截取点,再依次连结这些点,得到正n边形,求n的值.
图1 图2
素养探究全练
15.【运算能力】如图所示,M,N分别是☉O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,……,正n边形ABCDE…的AB,BC上的点,且BM=CN,连结OM,ON.
(1)求第1个图中∠MON的度数;
(2)第2个图中∠MON的度数是 ,第3个图中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形的边数n的关系.(直接写出答案)
16.【推理能力】教材的“课题学习”要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如图所示的步骤折叠:
请你根据小明同学的折叠方法,回答以下问题:
(1)如果设正三角形ABC的边长为a,那么CO= (用含a的式子表示);
(2)根据折叠的性质可以知道△CDE的形状为 三角形;
(3)请利用(1)(2)中的结论,证明六边形KHGFED是一个正六边形.
答案全解全析
基础过关全练
1.A ②中的说法错误,例如圆外切多边形是菱形,而菱形各边相等,但不是正多边形;③中的说法错误,例如圆内接多边形是矩形,而矩形各个角都是90°,都相等,但不是正多边形.故正确的说法为①④.
2.证明 ∵△OAB是正三角形,∴∠AOB=∠OAB=∠OBA=60°,∴∠DOE=∠AOB=60°,∵FC∥AB,
∴∠AOF=∠OAB=60°,∠BOC=∠OBA=60°,∴∠COD=∠AOF=60°,∠EOF=∠BOC=60°,∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,∴=====,∴AB=BC=CD=DE=EF=AF,=====,∴∠BAF=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,
∴六边形ABCDEF是正六边形.
3.C 连结OB、OC,如图,∵☉O的周长等于6π,∴☉O的半径OB=OC==3,∵六边形ABCDEF是正六边形,∴∠BOC==60°,∴△BOC是等边三角形,∴AB=BD,∴BC=OB=OC=3,即正六边形的边长为3.
4.B ∵六边形ABCDEF是正六边形,∴AB=AF=EF,∠BAF==120°,∴∠ABF=∠AFB==
30°,同理∠EAF=30°,∴∠1=180°-30°-30°=120°.
5.144°
解析 正五边形的内角=(5-2)×180°÷5=108°,∴∠E=∠D=108°,∵AE,CD分别与☉O相切于A,C两点,∴∠OAE=∠OCD=90°,∴∠AOC=540°-90°-90°-108°-108°=144°.
6.15°或105°
解析 本题易因考虑不全而致错.分情况求解如下:
(1)如图1,∠BAC=∠CAO-∠BAO=60°-45°=15°;
(2)如图2,∠BAC=∠BAE+∠EAC=90°+15°=105°.
综上所述,∠BAC的度数为15°或105°.
7.-1
解析 在☉O的内接正五边形ABCDE中,设EG=x,易知∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,∴AB=BG=AE=2,
∵∠AEG=∠BEA,∠EAG=∠EBA,∴△AEG∽△BEA,∴=,
∴AE2=EG·EB,∴22=x(x+2),解得x1=-1+,x2=-1-(舍去),
∴EG=-1.
8.解析 如图所示,连结OB、OC,∵多边形ABCDEF是正六边形,∴∠BOC=60°,∵OB=OC=4,∴△BOC是等边三角形,∴BC=OC=OB=4,∠OBM=60°,∴BM=2,∴OM=BM=2,
∴这个正六边形的边长为4,边心距OM的长为2.
9.解析 如图,先画圆,再画两条互相垂直的直径AE,CG,将圆弧4等分,再画出,所对弦的垂直平分线HD,FB,这样就将圆弧8等分,最后顺次连结各等分点得到正八边形ABCDEFGH.
能力提升全练
10.D ∵五边形ABCDE是正五边形,∴∠BAE==108°,∠COD==72°,∴∠BAE-∠COD=108°-72°=36°.
11.A 如图,设中间正六边形的中心为D,连结DB.∵点P,Q的坐标分别为(-2,3),(0,-3),图中是7个全等的正六边形,∴AB=BC=2,OQ=3,∴OA=OB=,∴OC=3,易知∠ODB=60°,∴OD=1,CM=DQ=DB=2,∴M(3,-2).
12.C 如图,AB是正十二边形的一条边,点O是正十二边形的中心,过A作AM⊥OB于M,在正十二边形中,∠AOB=360°÷12=30°,设OA=1,则AM=OA=,∴S△AOB=OB·AM=×1×=,∴正十二边形的面积为12×=3,∴3=12×π,∴π=3,∴π的估计值为3.
13.解析 (1)根据托勒密定理可得AC·BD=AB·CD+AD·BC,故答案为AC·BD=AB·CD+AD·BC.
(2)如图,连结AD、AC.∵五边形ABCDE是正五边形,∴△ABC≌△DCB≌△AED,∴AB=BC=CD=2,AC=BD=AD,设AC=BD=AD=x.在圆内接四边形ABCD中,由托勒密定理可得AC·BD=AB·CD+AD·BC,即x2=2×2+x·2,解得x1=1+,x2=1-(舍去),∴对角线BD的长为1+.
14.解析 (1)∵五边形ABCDE是正五边形,∴∠ABC==108°,即∠ABC=108°.
(2)△AMN是正三角形.理由:如图,连结ON,NF,由题意可得FN=ON=OF,∴△FON是等边三角形,∴∠NFA=60°,∴∠NMA=60°,同理可得∠ANM=60°,∴∠MAN=60°,∴△MAN是正三角形.
(3)如图,连结OD,∵∠AMN=60°,∴∠AON=120°,∵∠AOD=×2=144°,
∴∠NOD=∠AOD-∠AON=144°-120°=24°,
∵360°÷24°=15,∴n的值是15.
素养探究全练
15.解析 (1)如图所示,连结OB,OC,
∵△ABC为正三角形,∴∠BOC=120°,∵OC=OB,∴∠OBC=∠OCB=30°,∴∠OBM=60°-30°=30°,∴∠OBM=∠OCN,又∵BM=CN,OB=OC,∴△OMB≌△ONC,∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
(2)90°;72°.
(3)∠MON=.
16.解析 (1)∵正三角形ABC的边长为a,由折叠的性质可知,点O是三角形的重心,∴CO=a.
(2)△CDE为等边三角形.
(3)证明:由(2)知△CDE为等边三角形,∴CD=CE=DE=CO÷cos 30°=a,∠ADE=∠BED=120°,同理可得AH=AK=KH=a,BG=BF=GF=a,∠CKH=∠BHK=120°,∠CFG=∠AGF=
120°,∵AB=BC=AC=a,∴DE=DK=KH=HG=GF=FE=a,
∵∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°,
∴六边形KHGFED是一个正六边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
第27章 圆
27.4 正多边形和圆
基础过关全练
知识点1 圆内接正多边形及相关定义
1.【易错题】(2022吉林长春宽城期末)给出下列说法:①各边相等的圆内接多边形是正多边形;②各边相等的圆外切多边形是正多边形;③各角相等的圆内接多边形是正多边形;④各角相等的圆外切多边形是正多边形.其中正确的是( )
A.①④ B.②③
C.①③ D.②④
2.(2022广东潮州饶平英才实验中学月考)如图所示,△OAB为正三角形,以点O为圆心,OA长为半径作☉O,直径FC∥AB,AO,BO的延长线分别交☉O于点D,E,连结DE、EF、AF、CD、BC.求证:六边形ABCDEF是正六边形.
知识点2 圆内接正多边形的相关计算
3.(2022四川成都中考)如图,正六边形ABCDEF内接于☉O,若☉O的周长等于6π,则正六边形的边长为( )
A. B. C.3 D.2
4.【跨学科·化学】(2023湖南衡阳船山实验中学模拟)苯分子的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子与6个氢原子均在同一平面内,且所有碳碳键的键长都相等(如图1),组成了一个完美的六边形(正六边形),图2是其平面示意图,则∠1的度数为( )
A.130° B.120°
C.110° D.60°
5.(2023重庆万州模拟)如图,☉O与正五边形ABCDE的两边AE,CD分别相切于A,C两点,则∠AOC的度数是 .
6.【易错题】(2023四川成都武侯模拟)已知AB、AC分别是同一个圆的内接正方形和内接正六边形的边,那么∠BAC的度数是 .
7.(2023河南驻马店驿城期末)如图,☉O的内接正五边形ABCDE的对角线AD与BE相交于点G,AE=2,则EG的长是 .
8.(2023浙江温州鹿城期末)如图,正六边形ABCDEF内接于☉O,半径r=4,求这个正六边形的边长和边心距OM的长.
知识点3 正多边形的画法
9.剪纸艺术是最古老的中国民间艺术之一,山东烟台的剪纸是其中比较有代表性的.传统的剪纸先通过对折的方式将纸等分,小颖想通过将圆形纸片八等分的方式作正多边形,请你帮小颖利用直尺和圆规作一个正八边形.
能力提升全练
10.(2023安徽中考,6,★☆☆)如图,正五边形ABCDE内接于☉O,连结OC,OD,则∠BAE-∠COD=( )
A.60° B.54° C.48° D.36°
11.【新素材】(2023山西中考,10,★★☆)蜂巢结构精巧,其巢房横截面的形状均为正六边形.下图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点P,Q,M均为正六边形的顶点.若点P,Q的坐标分别为(-2,3),(0,-3),则点M的坐标为( )
A.(3,-2) B.(3,2)
C.(2,-3) D.(-2,-3)
12.【数学文化】(2023福建中考,10,★☆☆)中国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣.”“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,☉O的半径为1,运用“割圆术”,以圆内接正六边形的面积近似估计☉O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为( )
A. B.2
C.3 D.2
13.【新素材】(2022山西大同新荣模拟,23,★☆☆)阅读与思考
请阅读下列材料,并完成相应的任务:
克罗狄斯·托勒密(约90年~168年),是希腊数学家,天文学家,地理学家和占星家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理,托勒密定理的内容如下:圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.如图1,若四边形ABCD内接于☉O,则有 .任务:
(1)材料中划横线部分应填写的内容为 ;
(2)如图2,正五边形ABCDE内接于☉O,AB=2,求对角线BD的长.
图1
图2
14.【新考法】(2022浙江金华中考,22,★★☆)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答问题:
作法:如图2.
1.作直径AF.
2.以F为圆心,FO的长为半径作圆弧,与☉O交于点M,N.
3.连结AM,MN,NA.
(1)求∠ABC的度数;
(2)△AMN是正三角形吗 请说明理由;
(3)从点A开始,以DN的长为半径,在☉O上依次截取点,再依次连结这些点,得到正n边形,求n的值.
图1 图2
素养探究全练
15.【运算能力】如图所示,M,N分别是☉O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,……,正n边形ABCDE…的AB,BC上的点,且BM=CN,连结OM,ON.
(1)求第1个图中∠MON的度数;
(2)第2个图中∠MON的度数是 ,第3个图中∠MON的度数是 ;
(3)试探究∠MON的度数与正n边形的边数n的关系.(直接写出答案)
16.【推理能力】教材的“课题学习”要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如图所示的步骤折叠:
请你根据小明同学的折叠方法,回答以下问题:
(1)如果设正三角形ABC的边长为a,那么CO= (用含a的式子表示);
(2)根据折叠的性质可以知道△CDE的形状为 三角形;
(3)请利用(1)(2)中的结论,证明六边形KHGFED是一个正六边形.
答案全解全析
基础过关全练
1.A ②中的说法错误,例如圆外切多边形是菱形,而菱形各边相等,但不是正多边形;③中的说法错误,例如圆内接多边形是矩形,而矩形各个角都是90°,都相等,但不是正多边形.故正确的说法为①④.
2.证明 ∵△OAB是正三角形,∴∠AOB=∠OAB=∠OBA=60°,∴∠DOE=∠AOB=60°,∵FC∥AB,
∴∠AOF=∠OAB=60°,∠BOC=∠OBA=60°,∴∠COD=∠AOF=60°,∠EOF=∠BOC=60°,∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,∴=====,∴AB=BC=CD=DE=EF=AF,=====,∴∠BAF=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,
∴六边形ABCDEF是正六边形.
3.C 连结OB、OC,如图,∵☉O的周长等于6π,∴☉O的半径OB=OC==3,∵六边形ABCDEF是正六边形,∴∠BOC==60°,∴△BOC是等边三角形,∴AB=BD,∴BC=OB=OC=3,即正六边形的边长为3.
4.B ∵六边形ABCDEF是正六边形,∴AB=AF=EF,∠BAF==120°,∴∠ABF=∠AFB==
30°,同理∠EAF=30°,∴∠1=180°-30°-30°=120°.
5.144°
解析 正五边形的内角=(5-2)×180°÷5=108°,∴∠E=∠D=108°,∵AE,CD分别与☉O相切于A,C两点,∴∠OAE=∠OCD=90°,∴∠AOC=540°-90°-90°-108°-108°=144°.
6.15°或105°
解析 本题易因考虑不全而致错.分情况求解如下:
(1)如图1,∠BAC=∠CAO-∠BAO=60°-45°=15°;
(2)如图2,∠BAC=∠BAE+∠EAC=90°+15°=105°.
综上所述,∠BAC的度数为15°或105°.
7.-1
解析 在☉O的内接正五边形ABCDE中,设EG=x,易知∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,∴AB=BG=AE=2,
∵∠AEG=∠BEA,∠EAG=∠EBA,∴△AEG∽△BEA,∴=,
∴AE2=EG·EB,∴22=x(x+2),解得x1=-1+,x2=-1-(舍去),
∴EG=-1.
8.解析 如图所示,连结OB、OC,∵多边形ABCDEF是正六边形,∴∠BOC=60°,∵OB=OC=4,∴△BOC是等边三角形,∴BC=OC=OB=4,∠OBM=60°,∴BM=2,∴OM=BM=2,
∴这个正六边形的边长为4,边心距OM的长为2.
9.解析 如图,先画圆,再画两条互相垂直的直径AE,CG,将圆弧4等分,再画出,所对弦的垂直平分线HD,FB,这样就将圆弧8等分,最后顺次连结各等分点得到正八边形ABCDEFGH.
能力提升全练
10.D ∵五边形ABCDE是正五边形,∴∠BAE==108°,∠COD==72°,∴∠BAE-∠COD=108°-72°=36°.
11.A 如图,设中间正六边形的中心为D,连结DB.∵点P,Q的坐标分别为(-2,3),(0,-3),图中是7个全等的正六边形,∴AB=BC=2,OQ=3,∴OA=OB=,∴OC=3,易知∠ODB=60°,∴OD=1,CM=DQ=DB=2,∴M(3,-2).
12.C 如图,AB是正十二边形的一条边,点O是正十二边形的中心,过A作AM⊥OB于M,在正十二边形中,∠AOB=360°÷12=30°,设OA=1,则AM=OA=,∴S△AOB=OB·AM=×1×=,∴正十二边形的面积为12×=3,∴3=12×π,∴π=3,∴π的估计值为3.
13.解析 (1)根据托勒密定理可得AC·BD=AB·CD+AD·BC,故答案为AC·BD=AB·CD+AD·BC.
(2)如图,连结AD、AC.∵五边形ABCDE是正五边形,∴△ABC≌△DCB≌△AED,∴AB=BC=CD=2,AC=BD=AD,设AC=BD=AD=x.在圆内接四边形ABCD中,由托勒密定理可得AC·BD=AB·CD+AD·BC,即x2=2×2+x·2,解得x1=1+,x2=1-(舍去),∴对角线BD的长为1+.
14.解析 (1)∵五边形ABCDE是正五边形,∴∠ABC==108°,即∠ABC=108°.
(2)△AMN是正三角形.理由:如图,连结ON,NF,由题意可得FN=ON=OF,∴△FON是等边三角形,∴∠NFA=60°,∴∠NMA=60°,同理可得∠ANM=60°,∴∠MAN=60°,∴△MAN是正三角形.
(3)如图,连结OD,∵∠AMN=60°,∴∠AON=120°,∵∠AOD=×2=144°,
∴∠NOD=∠AOD-∠AON=144°-120°=24°,
∵360°÷24°=15,∴n的值是15.
素养探究全练
15.解析 (1)如图所示,连结OB,OC,
∵△ABC为正三角形,∴∠BOC=120°,∵OC=OB,∴∠OBC=∠OCB=30°,∴∠OBM=60°-30°=30°,∴∠OBM=∠OCN,又∵BM=CN,OB=OC,∴△OMB≌△ONC,∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
(2)90°;72°.
(3)∠MON=.
16.解析 (1)∵正三角形ABC的边长为a,由折叠的性质可知,点O是三角形的重心,∴CO=a.
(2)△CDE为等边三角形.
(3)证明:由(2)知△CDE为等边三角形,∴CD=CE=DE=CO÷cos 30°=a,∠ADE=∠BED=120°,同理可得AH=AK=KH=a,BG=BF=GF=a,∠CKH=∠BHK=120°,∠CFG=∠AGF=
120°,∵AB=BC=AC=a,∴DE=DK=KH=HG=GF=FE=a,
∵∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°,
∴六边形KHGFED是一个正六边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
