2024华东师大版数学九年级下学期课时练 第26章 二次函数素养综合检测(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练 第26章 二次函数素养综合检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
第26章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2022山西运城盐湖新康国际实验学校月考)下列y关于x的函数中,一定是二次函数的是( )
A.y=ax2+bx+c B.y=
C.y=(a2+1)x2 D.y=ax2
2.(2023湖南长沙雅礼教育集团期末)将抛物线y=3x2先向右平移2个单位,再向上平移6个单位,所得抛物线对应的函数表达式为( )
A.y=3(x-2)2+6 B.y=3(x-2)2-6
C.y=3(x+2)2+6 D.y=3(x+2)2-6
3.(2023广东珠海香洲期中)如图,抛物线y1=ax2+c与直线y2=mx+n交于A(-1,p),B(3,q)两点,则不等式y1A.x>-1 B.x<3
C.x<-3或x>1 D.-14.(2022江苏南通海安期中)若二次函数y=ax2+bx+c的图象与x轴相交于(1,0)、(4,0)两点,则一元二次方程ax2+bx+c=0的解为( )
A.x1=-1,x2=-4 B.x1=1,x2=4
C.x1=-1,x2=4 D.x1=1,x2=-4
5.(2023江苏无锡梁溪连元英禾双语学校模拟)关于二次函数y=x2-4x+5,下列结论中正确的是( )
A.图象的对称轴过点(2,0)
B.当x>-2时,y随x的增大而增大
C.图象与x轴有两个公共点
D.函数的最小值为5
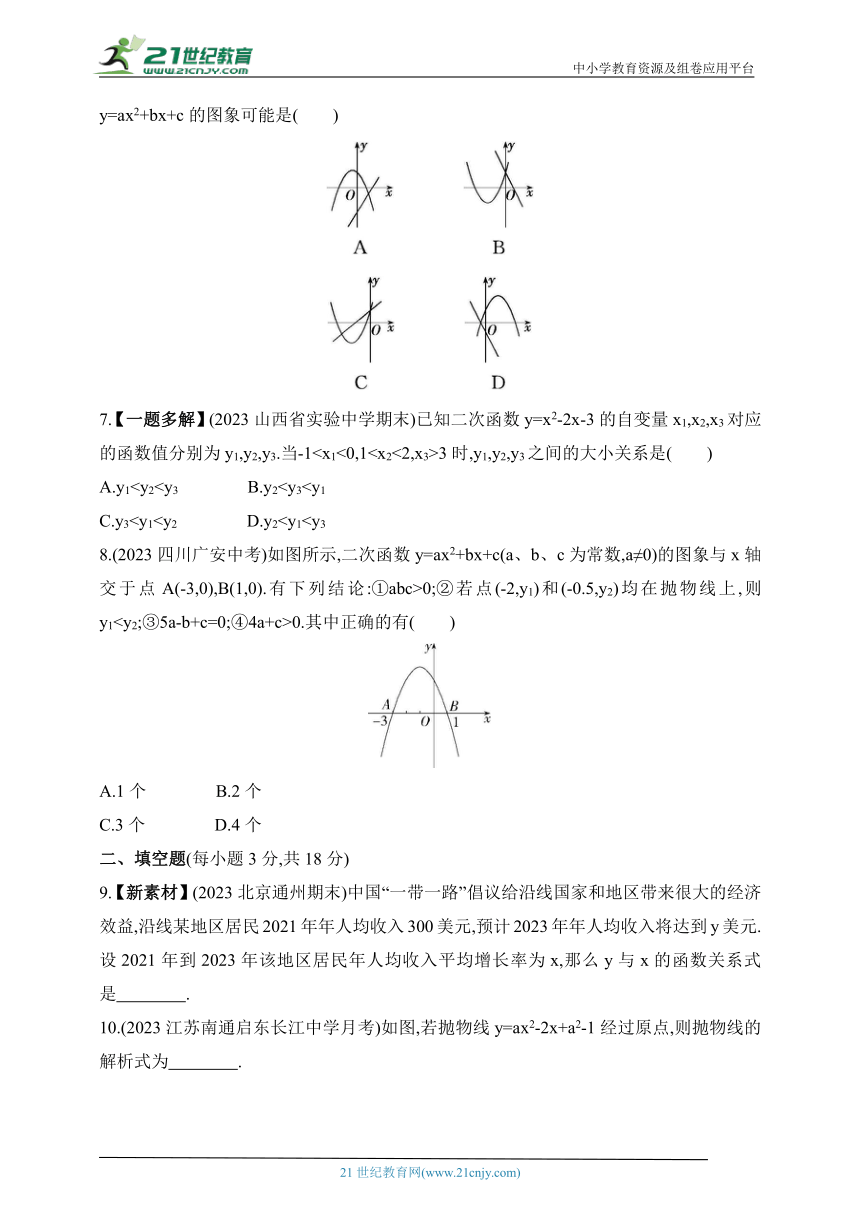
6.(2023河南周口太康期末)如图,在同一直角坐标系中,一次函数y=ax+b与二次函数y=ax2+bx+c的图象可能是( )
7.【一题多解】(2023山西省实验中学期末)已知二次函数y=x2-2x-3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当-13时,y1,y2,y3之间的大小关系是( )
A.y1C.y38.(2023四川广安中考)如图所示,二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象与x轴交于点A(-3,0),B(1,0).有下列结论:①abc>0;②若点(-2,y1)和(-0.5,y2)均在抛物线上,则y10.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
二、填空题(每小题3分,共18分)
9.【新素材】(2023北京通州期末)中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2021年年人均收入300美元,预计2023年年人均收入将达到y美元.设2021年到2023年该地区居民年人均收入平均增长率为x,那么y与x的函数关系式是 .
10.(2023江苏南通启东长江中学月考)如图,若抛物线y=ax2-2x+a2-1经过原点,则抛物线的解析式为 .
11.(2023山东泰安中考)二次函数y=-x2-3x+4的最大值是 .
12.【跨学科·体育与健康】(2023湖北宜昌中考)如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=-(x-10)(x+4),则铅球推出的距离OA= m.
13.【易错题】(2023海南海口华侨中学期末)对称轴与y轴平行且经过原点O的抛物线也经过A(2,m),B(4,m),若△AOB的面积为4,则抛物线的解析式为 .
14.【新考法】(2023四川眉山苏祠中学期中)距离地面有一定高度的某发射装置竖直向上发射物体,物体离地面的高度h(米)与物体运动的时间t(秒)之间满足函数关系式h=-5t2+mt+n,其图象如图所示,物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒.设w表示0秒到t秒时h的值的“极差”(即0秒到t秒时h的最大值与最小值的差),则当0≤t≤1时,w的取值范围是 ;当2≤t≤3时,w的取值范围是 .
三、解答题(共58分)
15.(2023湖北宜昌枝江马家店中学月考)(6分)已知函数y=(k+2)是关于x的二次函数.
(1)求k的值;
(2)当k为何值时,抛物线有最低点
(3)当k为何值时,函数有最大值
16.(2023河南开封金明中学月考)(6分)已知二次函数y=ax2+bx+c的图象经过A(1,5)、B(0,3)、C(-1,-3)三点.
(1)求这个函数的解析式;
(2)用配方法求出这个二次函数图象的顶点坐标.
17.(2023辽宁铁岭中考)(6分)商店出售某品牌护眼灯,每台进价为40元,在销售过程中发现,月销量y(台)与销售单价x(元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
销售单价x(元) … 50 60 70 …
月销量y(台) … 90 80 70 …
(1)求y与x之间的函数关系式;
(2)当护眼灯销售单价定为多少元时,商店每月出售这种护眼灯所获利润最大 最大月利润为多少元
18.(6分)如图,要在夹角为30°的两条小路OA和OB形成的角状空地上建一个三角形花坛,分别在边OA和OB上取点P和点Q,并扎起篱笆将花坛保护起来(篱笆的厚度忽略不计).若OP和OQ两段篱笆的总长为40 m,求该三角形花坛POQ面积的最大值.
19.(2023重庆九龙坡模拟)(10分)如图,建立平面直角坐标系xOy,x轴平行于地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在y=kx-(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)当k=2时,求炮弹飞行的最大海拔高度;
(2)若炮弹飞行的最大射程为5千米,求k的值;
(3)炮弹的最大射程为 千米(结果用含k的代数式表示).
20.(2023吉林长春朝阳模拟)(10分)如图,点P(a,3)在抛物线l:y=4-(6-x)2上,且在l的对称轴右侧.
(1)写出抛物线l的对称轴和y的最大值,并求出a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及抛物线l的一段,分别记为P',l'.平移该胶片,使l'所在抛物线对应的函数解析式恰为y=-x2+6x-9.求点P'移动的最短距离.
21.【分类讨论思想】(2023江苏扬州中考)(14分)在平面直角坐标系xOy中,已知点A在y轴正半轴上.
(1)如果四个点(0,0)、(0,2)、(1,1)、(-1,1)中恰有三个点在二次函数y=ax2(a为常数,且a≠0)的图象上.
①a= ;
②如图1,已知菱形ABCD的顶点B、C、D在该二次函数的图象上,且AD⊥y轴,求菱形的边长;
③如图2,已知正方形ABCD的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究n-m是不是定值.如果是,求出这个值;如果不是,请说明理由.
(2)已知正方形ABCD的顶点B、D在二次函数y=ax2(a为常数,且a>0)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.
答案全解全析
1.C A.当a=0时,原函数不是二次函数;B.分母含有自变量,不是二次函数;D.当a=0时,原函数不是二次函数.故选C.
2.A 将抛物线y=3x2先向右平移2个单位,再向上平移6个单位,所得抛物线对应的函数表达式为y=3(x-2)2+6.
3.D 由图象可知,当二次函数的图象在直线的下方时,-14.B 因为二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(4,0),
所以一元二次方程ax2+bx+c=0的解是x1=1,x2=4.
5.A y=x2-4x+5=(x-2)2+1,对称轴是直线x=2,则图象的对称轴过点(2,0);a=1>0,抛物线开口向上,对称轴是直线x=2,则当x>2时,y随x的增大而增大;函数的最小值是1,抛物线开口向上,则抛物线与x轴没有交点.故选A.
6.C A.由抛物线可知a<0,由直线可知a>0,故错误;B.由抛物线可知a>0,由直线可知a<0,故错误;C.由抛物线可知a>0,x=-<0,可得b>0,由直线可知a>0,b>0,故正确;D.由抛物线可知a<0,x=->0,可得b>0,由直线可知a<0,b<0,故错误.
7.D (解法1:利用函数性质)∵y=x2-2x-3=(x-1)2-4,∴对称轴为直线x=1,抛物线开口向上.∴当x>1时,y随x的增大而增大,∴y2∵x1,x2在对称轴两侧,且x1离对称轴较远,∴y2(解法2:数形结合)∵抛物线y=x2-2x-3=(x-1)2-4,∴对称轴为直线x=1,顶点坐标为(1,-4),当y=0时,x=-1或x=3,∴抛物线与x轴的两个交点坐标为(-1,0),(3,0),如图,易知当-13时,y28.C 由图象可得a<0,c>0,x=-<0,∴b<0,则abc>0,故①正确;∵二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象与x轴交于点A(-3,0),B(1,0),∴该函数的对称轴为直线x==-1,∴x=-0.5和x=-1.5对应的函数值相等,当x<-1时,y随x的增大而增大,∴若点(-2,y1)和(-0.5,y2)均在抛物线上,则y1-1,∴b=2a,∵点(1,0)在该函数图象上,∴a+b+c=0,∴a+2a+c=0,即3a+c=0,∴5a-b+c=5a-2a+c=3a+c=0,故③正确;∵a+b+c=0,a<0,∴2a+b+c<0,∴2a+2a+c<0,即4a+c<0,故④错误.故选C.
9.y=300(x+1)2
解析 根据题意得函数关系式是y=300(x+1)2.
10.y=-x2-2x
解析 把(0,0)代入y=ax2-2x+a2-1得0=a2-1,解得a=±1,∵抛物线开口向下,∴a=-1,∴抛物线的解析式为y=-x2-2x.
11.
解析 y=-x2-3x+4=-+,∵a=-1<0,∴当x=-时,y取得最大值,最大值是.
12.10
解析 令y=0,则-(x-10)(x+4)=0,解得x=10或x=-4(不合题意,舍去),∴A(10,0),∴OA=10 m.
13.y=-x2+3x或y=x2-3x
解析 本题没有明确给出抛物线的开口方向及点A、B所在的象限,所以m的正负无法确定,易因考虑不周而致错.∵抛物线经过A(2,m),B(4,m),∴对称轴是直线x=3,AB=2,∵△AOB的面积为4,∴AB·|m|=4,∴m=±4.
①当m=4时,A(2,4),B(4,4),设抛物线的解析式为y=a(x-3)2+h,把(0,0)和(2,4)代入得解得∴抛物线的解析式为y=-(x-3)2+=-x2+3x.
②当m=-4时,A(2,-4),B(4,-4),设抛物线的解析式为y=a(x-3)2+h,把(0,0)和(2,-4)代入得解得∴抛物线的解析式为y=(x-3)2-=x2-3x.
综上所述,抛物线的解析式为y=-x2+3x或y=x2-3x.
14.0≤w≤5;5≤w≤20
解析 本题将抛物线与“极差”融为一体考查,设计新颖.∵物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒,∴抛物线h=-5t2+mt+n的顶点的纵坐标为20,且经过点(3,0),∴解得或(不合题意,舍去),∴抛物线的解析式为h=-5t2+10t+15,∵h=-5(t-1)2+20,∴抛物线最高点的坐标为(1,20).当t=0时,h=15,∵20-15=5,∴当0≤t≤1时,w的取值范围是0≤w≤5;当t=2时,h=15,当t=3时,h=0,∵20-15=5,20-0=20,∴当2≤t≤3时,w的取值范围是5≤w≤20.
15.解析 (1)∵函数y=(k+2)是关于x的二次函数,∴k2+3k-2=2,且k+2≠0,解得k1=1,k2=-4,∴k的值为1或-4.
(2)∵抛物线有最低点,∴图象开口向上,即k+2>0,∴k>-2,∴k=1.
(3)∵函数有最大值,∴图象开口向下,即k+2<0,∴k<-2,∴k=-4.
16.解析 (1)把A(1,5)、B(0,3)、C(-1,-3)代入二次函数y=ax2+bx+c,可得解得∴这个函数的解析式为y=-2x2+4x+3.
(2)y=-2x2+4x+3=-2(x-1)2+5,∴顶点坐标是(1,5).
17.解析 (1)设月销量y(台)与销售单价x(元)之间满足的一次函数关系式为y=kx+b(k≠0),把(50,90)和(60,80)代入得解得∴y与x之间的函数关系式为y=-x+140.
(2)设每月出售这种护眼灯所获利润为w元,根据题意得w=(x-40)y=(x-40)(-x+140)=-x2+180x-5 600=-(x-90)2+2 500,∵a=-1<0,且规定销售单价不高于进价的2倍,∴当护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获利润最大,最大月利润为-(80-90)2+2 500=
2 400元.
18.解析 如图,作PC⊥OB,垂足为点C,设OP的长为x m,则OQ的长为(40-x)m,∵∠POQ=30°,∴PC=OP=x m,∴S△POQ=×x(40-x)=-(x-20)2+100,∵-<0,∴当OP的长为20 m时,该三角形花坛POQ的面积最大,最大值为100 m2.
19.解析 (1)当k=2时,y=2x-×(1+22)x2=-x2+2x=-(x-4)2+4,∵-<0,
∴当x=4时,y取得最大值,此时y=4,即当k=2时,炮弹飞行的最大海拔高度是4千米.
(2)当x=5,y=0时,即0=k×5-(1+k2)×52,解得k1=2+,k2=2-,即k的值是2+或2-.
(3).详解:当y=0时,即0=kx-(1+k2)x2,解得x1=0,x2=,∴炮弹的最大射程为千米.
20.解析 (1)∵抛物线l:y=4-(6-x)2=-(x-6)2+4,∴抛物线的顶点为Q(6,4),对称轴为直线x=6,y的最大值为4,当y=3时,3=-(x-6)2+4,解得x=5或7,∵点P在对称轴的右侧,∴P(7,3),∴a=7.
(2)∵平移后的抛物线的解析式为y=-x2+6x-9=-(x-3)2,∴平移后的顶点坐标为(3,0),∵平移前抛物线的顶点坐标为(6,4),∴点P'移动的最短距离==5.
21.解析 (1)①令x=0得y=0,∴(0,0)在二次函数y=ax2(a为常数,且a≠0)的图象上,(0,2)不在二次函数y=ax2(a为常数,且a≠0)的图象上,
∵四个点(0,0)、(0,2)、(1,1)、(-1,1)中恰有三个点在二次函数y=ax2(a为常数,且a≠0)的图象上,∴二次函数y=ax2(a为常数,且a≠0)的图象上的三个点是(0,0)、(1,1)、(-1,1),把(1,1)代入y=ax2得a=1.
②设BC交y轴于E,如图1,设菱形的边长为2b,则AB=BC=CD=AD=2b,易知B,C关于y轴对称,∴BE=CE=b,
∴B(b,b2),∴OE=b2,∵AE==b,∴OA=OE+AE=b2+b,
∴D(2b,b2+b),把D(2b,b2+b)代入y=x2得b2+b=4b2,解得b=或b=0(舍去),∴菱形的边长为.
③n-m是定值,理由如下:过B作BF⊥y轴于F,过D作DE⊥y轴于E,如图2,∵点B、D的横坐标分别为m、n,∴B(m,m2),D(n,n2),∴BF=m,OF=m2,DE=n,OE=n2,∵四边形ABCD是正方形,∴∠DAB=90°,AD=AB,∴∠FAB=90°-∠EAD=∠EDA,∵∠AFB=∠DEA=90°,∴△ABF≌△DAE,∴BF=AE,AF=DE,∴m=n2-AF-m2,AF=n,∴m=n2-n-m2,∴m+n=(n-m)(n+m),∵点B、D在y轴的同侧,∴m+n≠0,∴n-m=1.
(2)过B作BF⊥y轴于F,过D作DE⊥y轴于E,∵点B、D的横坐标分别为m、n,∴B(m,am2),D(n,an2).
①当B,D在y轴左侧时,如图3,∴BF=-m,OF=am2,DE=-n,OE=an2,易证△ABF≌△DAE,∴BF=AE,AF=DE,∴-m=am2-AF-an2,AF=-n,
∴-m=am2+n-an2,∴m+n=a(n-m)(n+m),∵点B、D在y轴的同侧,∴m+n≠0,∴n-m=;
②当B在y轴左侧,D在y轴右侧时,如图4,∴BF=-m,OF=am2,DE=n,OE=an2,易证△ABF≌△DAE,∴BF=AE,AF=DE,
∴-m=am2+AF-an2,AF=n,∴-m=am2+n-an2,∴m+n=a(n+m)(n-m),∴m+n=0或n-m=;
③当B,D在y轴右侧时,如图5,∴BF=m,OF=am2,DE=n,OE=an2,易证△ABF≌△DAE,∴BF=AE,AF=DE,∴m=an2-AF-am2,AF=n,∴m=an2-n-am2,∴m+n=a(n+m)(n-m),∵点B、D在y轴的同侧,∴m+n≠0,∴n-m=.
综上所述,m、n满足的等量关系式为m+n=0或n-m=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
第26章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2022山西运城盐湖新康国际实验学校月考)下列y关于x的函数中,一定是二次函数的是( )
A.y=ax2+bx+c B.y=
C.y=(a2+1)x2 D.y=ax2
2.(2023湖南长沙雅礼教育集团期末)将抛物线y=3x2先向右平移2个单位,再向上平移6个单位,所得抛物线对应的函数表达式为( )
A.y=3(x-2)2+6 B.y=3(x-2)2-6
C.y=3(x+2)2+6 D.y=3(x+2)2-6
3.(2023广东珠海香洲期中)如图,抛物线y1=ax2+c与直线y2=mx+n交于A(-1,p),B(3,q)两点,则不等式y1
C.x<-3或x>1 D.-1
A.x1=-1,x2=-4 B.x1=1,x2=4
C.x1=-1,x2=4 D.x1=1,x2=-4
5.(2023江苏无锡梁溪连元英禾双语学校模拟)关于二次函数y=x2-4x+5,下列结论中正确的是( )
A.图象的对称轴过点(2,0)
B.当x>-2时,y随x的增大而增大
C.图象与x轴有两个公共点
D.函数的最小值为5
6.(2023河南周口太康期末)如图,在同一直角坐标系中,一次函数y=ax+b与二次函数y=ax2+bx+c的图象可能是( )
7.【一题多解】(2023山西省实验中学期末)已知二次函数y=x2-2x-3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当-1
A.y1
A.1个 B.2个
C.3个 D.4个
二、填空题(每小题3分,共18分)
9.【新素材】(2023北京通州期末)中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2021年年人均收入300美元,预计2023年年人均收入将达到y美元.设2021年到2023年该地区居民年人均收入平均增长率为x,那么y与x的函数关系式是 .
10.(2023江苏南通启东长江中学月考)如图,若抛物线y=ax2-2x+a2-1经过原点,则抛物线的解析式为 .
11.(2023山东泰安中考)二次函数y=-x2-3x+4的最大值是 .
12.【跨学科·体育与健康】(2023湖北宜昌中考)如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=-(x-10)(x+4),则铅球推出的距离OA= m.
13.【易错题】(2023海南海口华侨中学期末)对称轴与y轴平行且经过原点O的抛物线也经过A(2,m),B(4,m),若△AOB的面积为4,则抛物线的解析式为 .
14.【新考法】(2023四川眉山苏祠中学期中)距离地面有一定高度的某发射装置竖直向上发射物体,物体离地面的高度h(米)与物体运动的时间t(秒)之间满足函数关系式h=-5t2+mt+n,其图象如图所示,物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒.设w表示0秒到t秒时h的值的“极差”(即0秒到t秒时h的最大值与最小值的差),则当0≤t≤1时,w的取值范围是 ;当2≤t≤3时,w的取值范围是 .
三、解答题(共58分)
15.(2023湖北宜昌枝江马家店中学月考)(6分)已知函数y=(k+2)是关于x的二次函数.
(1)求k的值;
(2)当k为何值时,抛物线有最低点
(3)当k为何值时,函数有最大值
16.(2023河南开封金明中学月考)(6分)已知二次函数y=ax2+bx+c的图象经过A(1,5)、B(0,3)、C(-1,-3)三点.
(1)求这个函数的解析式;
(2)用配方法求出这个二次函数图象的顶点坐标.
17.(2023辽宁铁岭中考)(6分)商店出售某品牌护眼灯,每台进价为40元,在销售过程中发现,月销量y(台)与销售单价x(元)之间满足一次函数关系,规定销售单价不低于进价,且不高于进价的2倍,其部分对应数据如下表所示:
销售单价x(元) … 50 60 70 …
月销量y(台) … 90 80 70 …
(1)求y与x之间的函数关系式;
(2)当护眼灯销售单价定为多少元时,商店每月出售这种护眼灯所获利润最大 最大月利润为多少元
18.(6分)如图,要在夹角为30°的两条小路OA和OB形成的角状空地上建一个三角形花坛,分别在边OA和OB上取点P和点Q,并扎起篱笆将花坛保护起来(篱笆的厚度忽略不计).若OP和OQ两段篱笆的总长为40 m,求该三角形花坛POQ面积的最大值.
19.(2023重庆九龙坡模拟)(10分)如图,建立平面直角坐标系xOy,x轴平行于地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在y=kx-(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)当k=2时,求炮弹飞行的最大海拔高度;
(2)若炮弹飞行的最大射程为5千米,求k的值;
(3)炮弹的最大射程为 千米(结果用含k的代数式表示).
20.(2023吉林长春朝阳模拟)(10分)如图,点P(a,3)在抛物线l:y=4-(6-x)2上,且在l的对称轴右侧.
(1)写出抛物线l的对称轴和y的最大值,并求出a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及抛物线l的一段,分别记为P',l'.平移该胶片,使l'所在抛物线对应的函数解析式恰为y=-x2+6x-9.求点P'移动的最短距离.
21.【分类讨论思想】(2023江苏扬州中考)(14分)在平面直角坐标系xOy中,已知点A在y轴正半轴上.
(1)如果四个点(0,0)、(0,2)、(1,1)、(-1,1)中恰有三个点在二次函数y=ax2(a为常数,且a≠0)的图象上.
①a= ;
②如图1,已知菱形ABCD的顶点B、C、D在该二次函数的图象上,且AD⊥y轴,求菱形的边长;
③如图2,已知正方形ABCD的顶点B、D在该二次函数的图象上,点B、D在y轴的同侧,且点B在点D的左侧,设点B、D的横坐标分别为m、n,试探究n-m是不是定值.如果是,求出这个值;如果不是,请说明理由.
(2)已知正方形ABCD的顶点B、D在二次函数y=ax2(a为常数,且a>0)的图象上,点B在点D的左侧,设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式.
答案全解全析
1.C A.当a=0时,原函数不是二次函数;B.分母含有自变量,不是二次函数;D.当a=0时,原函数不是二次函数.故选C.
2.A 将抛物线y=3x2先向右平移2个单位,再向上平移6个单位,所得抛物线对应的函数表达式为y=3(x-2)2+6.
3.D 由图象可知,当二次函数的图象在直线的下方时,-1
所以一元二次方程ax2+bx+c=0的解是x1=1,x2=4.
5.A y=x2-4x+5=(x-2)2+1,对称轴是直线x=2,则图象的对称轴过点(2,0);a=1>0,抛物线开口向上,对称轴是直线x=2,则当x>2时,y随x的增大而增大;函数的最小值是1,抛物线开口向上,则抛物线与x轴没有交点.故选A.
6.C A.由抛物线可知a<0,由直线可知a>0,故错误;B.由抛物线可知a>0,由直线可知a<0,故错误;C.由抛物线可知a>0,x=-<0,可得b>0,由直线可知a>0,b>0,故正确;D.由抛物线可知a<0,x=->0,可得b>0,由直线可知a<0,b<0,故错误.
7.D (解法1:利用函数性质)∵y=x2-2x-3=(x-1)2-4,∴对称轴为直线x=1,抛物线开口向上.∴当x>1时,y随x的增大而增大,∴y2
9.y=300(x+1)2
解析 根据题意得函数关系式是y=300(x+1)2.
10.y=-x2-2x
解析 把(0,0)代入y=ax2-2x+a2-1得0=a2-1,解得a=±1,∵抛物线开口向下,∴a=-1,∴抛物线的解析式为y=-x2-2x.
11.
解析 y=-x2-3x+4=-+,∵a=-1<0,∴当x=-时,y取得最大值,最大值是.
12.10
解析 令y=0,则-(x-10)(x+4)=0,解得x=10或x=-4(不合题意,舍去),∴A(10,0),∴OA=10 m.
13.y=-x2+3x或y=x2-3x
解析 本题没有明确给出抛物线的开口方向及点A、B所在的象限,所以m的正负无法确定,易因考虑不周而致错.∵抛物线经过A(2,m),B(4,m),∴对称轴是直线x=3,AB=2,∵△AOB的面积为4,∴AB·|m|=4,∴m=±4.
①当m=4时,A(2,4),B(4,4),设抛物线的解析式为y=a(x-3)2+h,把(0,0)和(2,4)代入得解得∴抛物线的解析式为y=-(x-3)2+=-x2+3x.
②当m=-4时,A(2,-4),B(4,-4),设抛物线的解析式为y=a(x-3)2+h,把(0,0)和(2,-4)代入得解得∴抛物线的解析式为y=(x-3)2-=x2-3x.
综上所述,抛物线的解析式为y=-x2+3x或y=x2-3x.
14.0≤w≤5;5≤w≤20
解析 本题将抛物线与“极差”融为一体考查,设计新颖.∵物体运动的最高点离地面20米,物体从发射到落地的运动时间为3秒,∴抛物线h=-5t2+mt+n的顶点的纵坐标为20,且经过点(3,0),∴解得或(不合题意,舍去),∴抛物线的解析式为h=-5t2+10t+15,∵h=-5(t-1)2+20,∴抛物线最高点的坐标为(1,20).当t=0时,h=15,∵20-15=5,∴当0≤t≤1时,w的取值范围是0≤w≤5;当t=2时,h=15,当t=3时,h=0,∵20-15=5,20-0=20,∴当2≤t≤3时,w的取值范围是5≤w≤20.
15.解析 (1)∵函数y=(k+2)是关于x的二次函数,∴k2+3k-2=2,且k+2≠0,解得k1=1,k2=-4,∴k的值为1或-4.
(2)∵抛物线有最低点,∴图象开口向上,即k+2>0,∴k>-2,∴k=1.
(3)∵函数有最大值,∴图象开口向下,即k+2<0,∴k<-2,∴k=-4.
16.解析 (1)把A(1,5)、B(0,3)、C(-1,-3)代入二次函数y=ax2+bx+c,可得解得∴这个函数的解析式为y=-2x2+4x+3.
(2)y=-2x2+4x+3=-2(x-1)2+5,∴顶点坐标是(1,5).
17.解析 (1)设月销量y(台)与销售单价x(元)之间满足的一次函数关系式为y=kx+b(k≠0),把(50,90)和(60,80)代入得解得∴y与x之间的函数关系式为y=-x+140.
(2)设每月出售这种护眼灯所获利润为w元,根据题意得w=(x-40)y=(x-40)(-x+140)=-x2+180x-5 600=-(x-90)2+2 500,∵a=-1<0,且规定销售单价不高于进价的2倍,∴当护眼灯销售单价定为80元时,商店每月出售这种护眼灯所获利润最大,最大月利润为-(80-90)2+2 500=
2 400元.
18.解析 如图,作PC⊥OB,垂足为点C,设OP的长为x m,则OQ的长为(40-x)m,∵∠POQ=30°,∴PC=OP=x m,∴S△POQ=×x(40-x)=-(x-20)2+100,∵-<0,∴当OP的长为20 m时,该三角形花坛POQ的面积最大,最大值为100 m2.
19.解析 (1)当k=2时,y=2x-×(1+22)x2=-x2+2x=-(x-4)2+4,∵-<0,
∴当x=4时,y取得最大值,此时y=4,即当k=2时,炮弹飞行的最大海拔高度是4千米.
(2)当x=5,y=0时,即0=k×5-(1+k2)×52,解得k1=2+,k2=2-,即k的值是2+或2-.
(3).详解:当y=0时,即0=kx-(1+k2)x2,解得x1=0,x2=,∴炮弹的最大射程为千米.
20.解析 (1)∵抛物线l:y=4-(6-x)2=-(x-6)2+4,∴抛物线的顶点为Q(6,4),对称轴为直线x=6,y的最大值为4,当y=3时,3=-(x-6)2+4,解得x=5或7,∵点P在对称轴的右侧,∴P(7,3),∴a=7.
(2)∵平移后的抛物线的解析式为y=-x2+6x-9=-(x-3)2,∴平移后的顶点坐标为(3,0),∵平移前抛物线的顶点坐标为(6,4),∴点P'移动的最短距离==5.
21.解析 (1)①令x=0得y=0,∴(0,0)在二次函数y=ax2(a为常数,且a≠0)的图象上,(0,2)不在二次函数y=ax2(a为常数,且a≠0)的图象上,
∵四个点(0,0)、(0,2)、(1,1)、(-1,1)中恰有三个点在二次函数y=ax2(a为常数,且a≠0)的图象上,∴二次函数y=ax2(a为常数,且a≠0)的图象上的三个点是(0,0)、(1,1)、(-1,1),把(1,1)代入y=ax2得a=1.
②设BC交y轴于E,如图1,设菱形的边长为2b,则AB=BC=CD=AD=2b,易知B,C关于y轴对称,∴BE=CE=b,
∴B(b,b2),∴OE=b2,∵AE==b,∴OA=OE+AE=b2+b,
∴D(2b,b2+b),把D(2b,b2+b)代入y=x2得b2+b=4b2,解得b=或b=0(舍去),∴菱形的边长为.
③n-m是定值,理由如下:过B作BF⊥y轴于F,过D作DE⊥y轴于E,如图2,∵点B、D的横坐标分别为m、n,∴B(m,m2),D(n,n2),∴BF=m,OF=m2,DE=n,OE=n2,∵四边形ABCD是正方形,∴∠DAB=90°,AD=AB,∴∠FAB=90°-∠EAD=∠EDA,∵∠AFB=∠DEA=90°,∴△ABF≌△DAE,∴BF=AE,AF=DE,∴m=n2-AF-m2,AF=n,∴m=n2-n-m2,∴m+n=(n-m)(n+m),∵点B、D在y轴的同侧,∴m+n≠0,∴n-m=1.
(2)过B作BF⊥y轴于F,过D作DE⊥y轴于E,∵点B、D的横坐标分别为m、n,∴B(m,am2),D(n,an2).
①当B,D在y轴左侧时,如图3,∴BF=-m,OF=am2,DE=-n,OE=an2,易证△ABF≌△DAE,∴BF=AE,AF=DE,∴-m=am2-AF-an2,AF=-n,
∴-m=am2+n-an2,∴m+n=a(n-m)(n+m),∵点B、D在y轴的同侧,∴m+n≠0,∴n-m=;
②当B在y轴左侧,D在y轴右侧时,如图4,∴BF=-m,OF=am2,DE=n,OE=an2,易证△ABF≌△DAE,∴BF=AE,AF=DE,
∴-m=am2+AF-an2,AF=n,∴-m=am2+n-an2,∴m+n=a(n+m)(n-m),∴m+n=0或n-m=;
③当B,D在y轴右侧时,如图5,∴BF=m,OF=am2,DE=n,OE=an2,易证△ABF≌△DAE,∴BF=AE,AF=DE,∴m=an2-AF-am2,AF=n,∴m=an2-n-am2,∴m+n=a(n+m)(n-m),∵点B、D在y轴的同侧,∴m+n≠0,∴n-m=.
综上所述,m、n满足的等量关系式为m+n=0或n-m=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
