2024华东师大版数学九年级下学期课时练--第27章 圆素养综合检测(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--第27章 圆素养综合检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 616.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 20:40:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
第27章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023江苏镇江期中)下列说法正确的是( )
A.弧长相等的弧是等弧
B.直径是最长的弦
C.三点确定一个圆
D.平分弦的直径垂直于弦
2.(2023河南中考)如图,点A,B,C在☉O上,若∠C=55°,则∠AOB的度数为( )
A.95° B.100°
C.105° D.110°
3.(2023四川广元苍溪期末)如图,点P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段OP的长为( )
A.3 B.3
C.6 D.9
4.【易错题】(2023四川泸州泸县模拟)在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆与x轴的位置关系是( )
A.相交 B.相离
C.相切 D.无法判断
5.(2023吉林松原前郭模拟)如图,四边形ABCD内接于☉O,AB是☉O的直径,EF与☉O相切于点A,若∠C=120°,则∠DAE的度数为( )
A.20° B.30° C.50° D.60°
6.【中华优秀传统文化】(2023湖北恩施州巴东期中)扇子最早称“翣”,在我国已有两千多年历史.“打开半个月亮,收起兜里可装,来时荷花初放,去时菊花正黄.”这则谜语说的就是扇子.如图,一竹扇完全打开后,外侧两竹条AB,AC的夹角为135°,AB的长为30 cm,扇面BD的长为
20 cm,则扇面的面积为( )
A.π cm2 B.600π cm2
C.300π cm2 D.30π cm2
7.【中华优秀传统文化】(2023陕西中考)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图2是从正面看到的一个“老碗”(图1)的形状示意图,是☉O的一部分,D是的中点,连结OD,与弦AB交于点C,连结OA,OB.已知AB=24 cm,碗深CD=8 cm,则☉O的半径OA为( )
A.13 cm B.16 cm
C.17 cm D.26 cm
8.【数学文化】【新考向·新定义试题】(2023湖南张家界中考)“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,三段圆弧围成的封闭图形就是“莱洛三角形”.若等边△ABC的边长为3,则该“莱洛三角形”的周长等于( )
A.π B.3π C.2π D.2π-
9.【新考法】(2023河南开封龙亭模拟)如图,☉O的半径为1,AD,BC是☉O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )
10.(2023湖南永州冷水滩京华中学期末)如图,PA、PB是☉O的切线,切点分别为A、B,BC是☉O的直径,PO交☉O于E点,连结AB交PO于F,连结CE交AB于D点,连结AC.下列结论:①PA=PB;②OP⊥AB;③CE平分∠ACB;④OF=AC;⑤E是△PAB的内心;⑥△CDA≌△EDF.其中一定成立的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题(每小题3分,共18分)
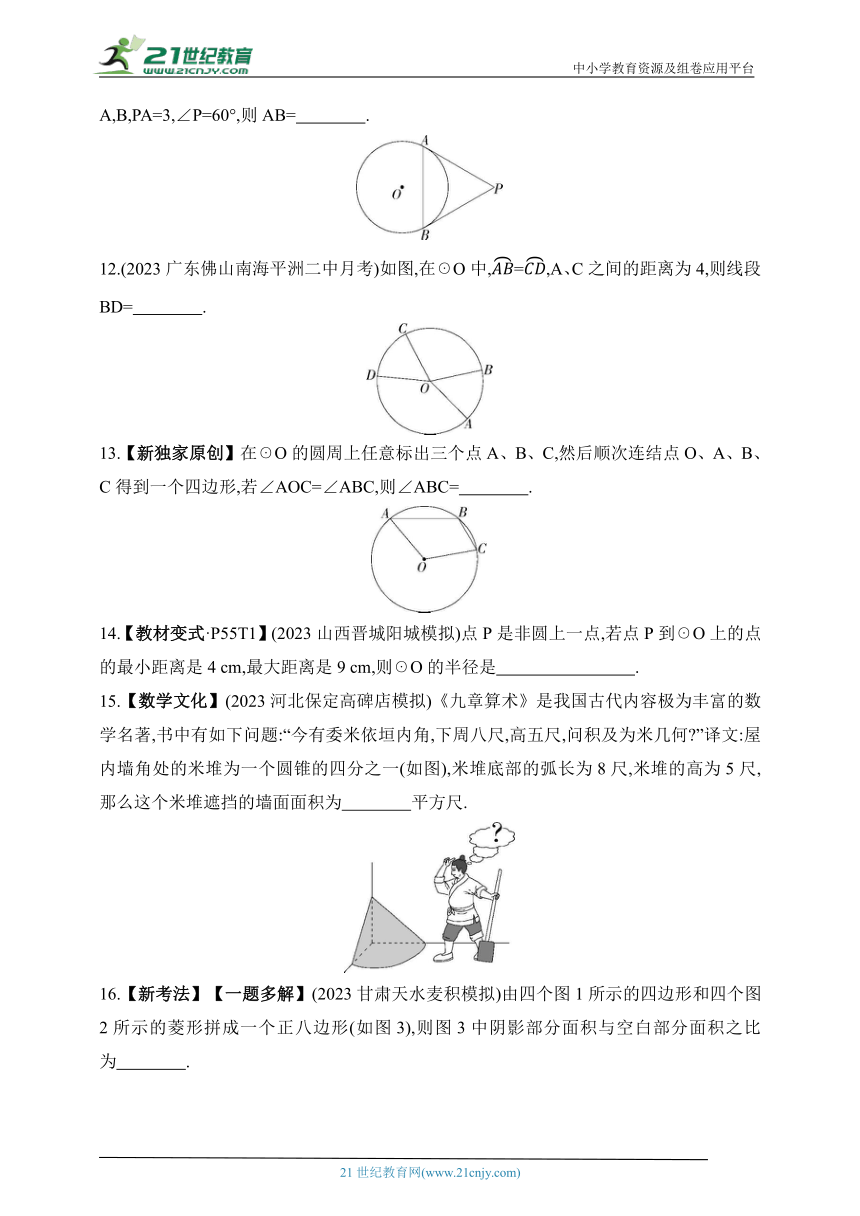
11.(2023浙江杭州保俶塔申花实验学校模拟)如图,PA,PB与☉O分别相切于点A,B,PA=3,∠P=60°,则AB= .
12.(2023广东佛山南海平洲二中月考)如图,在☉O中,=,A、C之间的距离为4,则线段BD= .
13.【新独家原创】在☉O的圆周上任意标出三个点A、B、C,然后顺次连结点O、A、B、C得到一个四边形,若∠AOC=∠ABC,则∠ABC= .
14.【教材变式·P55T1】(2023山西晋城阳城模拟)点P是非圆上一点,若点P到☉O上的点的最小距离是4 cm,最大距离是9 cm,则☉O的半径是 .
15.【数学文化】(2023河北保定高碑店模拟)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问积及为米几何 ”译文:屋内墙角处的米堆为一个圆锥的四分之一(如图),米堆底部的弧长为8尺,米堆的高为5尺,那么这个米堆遮挡的墙面面积为 平方尺.
16.【新考法】【一题多解】(2023甘肃天水麦积模拟)由四个图1所示的四边形和四个图2所示的菱形拼成一个正八边形(如图3),则图3中阴影部分面积与空白部分面积之比为 .
三、解答题(共52分)
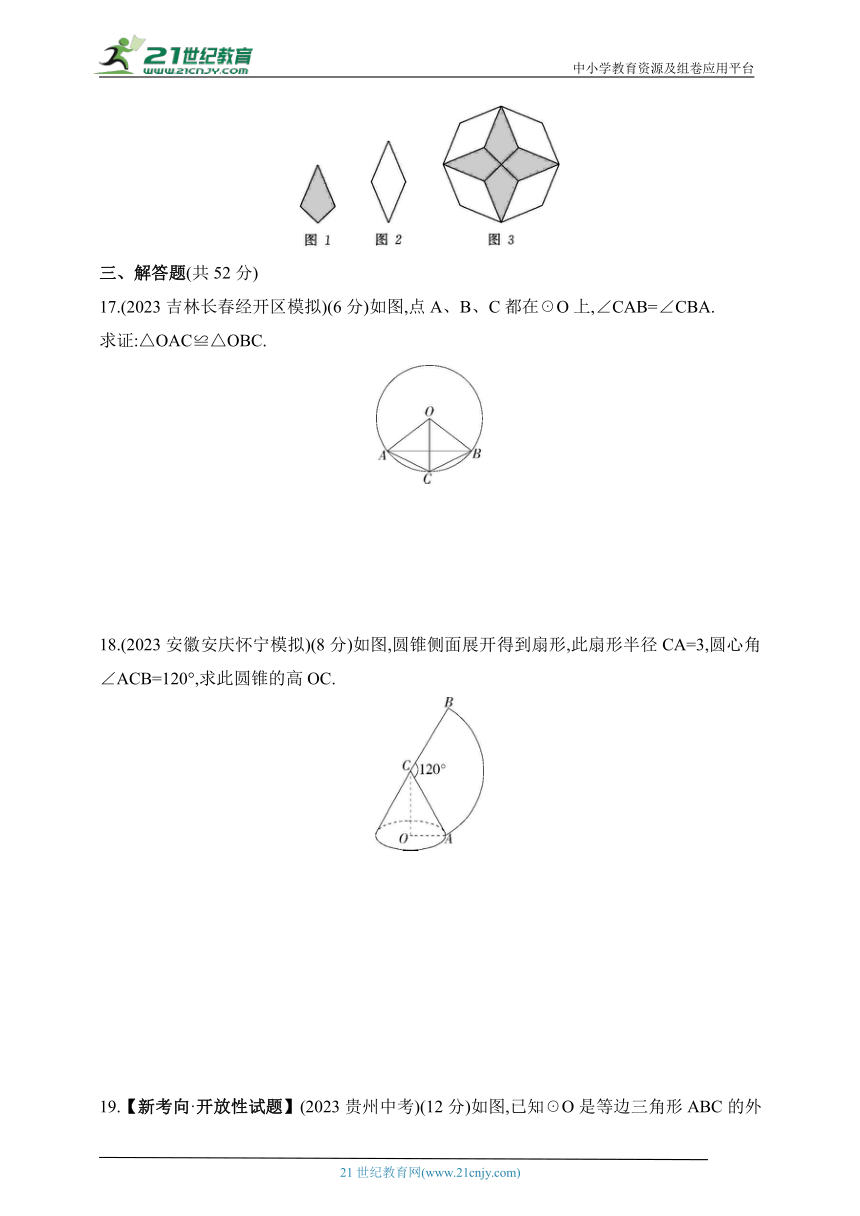
17.(2023吉林长春经开区模拟)(6分)如图,点A、B、C都在☉O上,∠CAB=∠CBA.
求证:△OAC≌△OBC.
18.(2023安徽安庆怀宁模拟)(8分)如图,圆锥侧面展开得到扇形,此扇形半径CA=3,圆心角∠ACB=120°,求此圆锥的高OC.
19.【新考向·开放性试题】(2023贵州中考)(12分)如图,已知☉O是等边三角形ABC的外接圆,连结CO并延长交AB于点D,交☉O于点E,连结EA,EB.
(1)写出图中一个度数为30°的角: ,图中与△ACD全等的三角形是 ;
(2)求证:△AED∽△CEB;
(3)连结OA,OB,判断四边形OAEB的形状,并说明理由.
20.(2023湖南常德中考)(12分)如图,四边形ABCD是☉O的内接四边形,AB是直径,C是的中点,过点C作CE⊥AD交AD的延长线于点E.
(1)求证:CE是☉O的切线;
(2)若BC=6,AC=8,求CE,DE的长.
21.【跨学科·物理】(14分)在古代,智慧的劳动人民已经会使用“石磨”(如图),其原理为在磨盘的边缘连结一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图1所示,两个固定长度的“连杆”AP,BP的连结点P在☉O上,当点P在☉O上转动时,带动点A,B分别在射线OM,ON上滑动,OM⊥ON.当AP与☉O相切时,点B恰好落在☉O上,如图2.
根据图2解答下列问题.
(1)求证:∠PAO=2∠PBO;
(2)若☉O的半径为5,AP=,求BP的长.
图1
图2
答案全解全析
1.B 能够重合的弧是等弧,故选项A说法错误;不在同一条直线上的三点确定一个圆,故选项C说法错误;平分弦(不是直径)的直径垂直于弦,故选项D说法错误.
2.D ∵∠AOB=2∠C,∠C=55°,∴∠AOB=110°.
3.C 如图,连结OA,∵PA为☉O的切线,∴∠OAP=90°,∵OB=3,∴AO=OB=3,∵∠P=30°,∴OP=2OA=6.
4.C 确定圆心与x轴的距离时易因弄错数据致错.∵圆心的坐标为
(-3,4),∴圆心与x轴距离为4,等于其半径4,∴以点(-3,4)为圆心,4为半径的圆与x轴的位置关系为相切.
5.B ∵四边形ABCD内接于☉O,∴∠C+∠DAB=180°,∵∠C=120°,∴∠DAB=60°,∵EF与☉O相切于点A,∴OA⊥EF,∴∠OAE=90°,∴∠DAE=∠OAE-∠DAB=30°.
6.C ∵AB=30 cm,BD=20 cm,∴AD=10 cm,∵∠BAC=135°,∴扇面的面积=-=-=300π(cm2).
7.A ∵是☉O的一部分,D是的中点,AB=24 cm,∴OD⊥AB,AC=BC=AB=12 cm.设☉O的半径OA为R cm,则OC=OD-CD=(R-8)cm.在Rt△OAC中,OA2=AC2+OC2,∴R2=122+(R-8)2,∴R=13,即☉O的半径OA为13 cm.
8.B ∵△ABC是等边三角形,∴AB=BC=AC=3,∠A=∠B=∠C=60°,∴==,∵的长==π,∴该“莱洛三角形”的周长是3π.
9.C 本题将函数图象与圆的性质融为一体考查,设计新颖.当P在OC上运动时,根据题意得sin∠APB=,∵OA=1,AP=x,y=sin∠APB,∴y=(110.A 如图,连结OA,BE,∵PA、PB是☉O的切线,∴PA=PB,故①正确;∵PA=PB,OA=OB,∴OP所在直线是AB的垂直平分线,∴OP⊥AB,故②正确;∵OP所在直线是AB的垂直平分线,∴=,∴∠ACE=∠BCE,∴CE平分∠ACB,故③正确;∵BC是☉O的直径,∴∠BAC=90°,∵∠BFO=90°,∴∠BAC=∠BFO,∴OF∥AC,∵OB=OC,
AF=BF,∴OF=AC,故④正确;∵PB是☉O的切线,∴∠PBE+∠EBC=90°,∵BC是☉O的直径,∴∠BEC=90°,∴∠EBC+∠ECB=90°,∴∠PBE=∠ECB,∵=,
∴∠ECB=∠EBA,∴∠PBE=∠EBA,∵∠APE=∠BPE,∴E是△PAB的内心,故⑤正确;∵AC∥OE,∴△CDA∽△EDF,故⑥错误.故选A.
11.3
解析 ∵PA,PB分别与☉O相切于点A,B,∴PA=PB,∵∠P=60°,∴△PAB是等边三角形,∴AB=PA=3.
12.4
解析 如图,连结BD,AC.∵=,∴+=+,∴=,∴BD=AC=4.
13.120°
解析 如图,在优弧AC上任取一点D,连结AD、CD,∵四边形ADCB是☉O的内接四边形,∴∠ADC+∠ABC=180°,∠ADC=∠AOC,∵∠AOC=∠ABC,
∴∠ADC=∠ABC,∴∠ABC+∠ABC=180°,∴∠ABC=120°.
14.6.5 cm或2.5 cm
解析 分两种情况讨论:
(1)当点在圆内时,如图1,∵点到圆上的点的最小距离PB=4 cm,最大距离PA=9 cm,∴直径AB=4+9=13(cm),∴半径为6.5 cm;
(2)当点在圆外时,如图2,∵点到圆上的最小距离PB=4 cm,最大距离PA=9 cm,∴直径AB=9-4=5(cm),∴半径为2.5 cm.
综上所述,圆O的半径为6.5 cm或2.5 cm.
15.
解析 设圆锥的底面半径为r尺,由米堆底部的弧长为8尺可得×2πr=8,解得r=,∴2×××5=(平方尺),∴这个米堆遮挡的墙面面积为平方尺.
16.
解析 本题将菱形和正多边形融合在一起,考查综合运用数学知识解决问题的能力.(解法1:局部求解)如图,正八边形的每个内角的度数为×(8-2)×180°=135°,∴∠ABC=∠BAP=135°,∴∠BAD=∠PAE=45°,
∴∠DAE=45°.在△ABD和△ADE中,∵AB=AD,∠BAD=∠DAE,AD=AE,∴△ABD≌△ADE,∴BD=DE,
∴DF=BD=DE=DG.由对称性易知四边形DEMN为正方形,∴OD=DG=DF.设S△CDF=a,则=4a,S△OCD=a,∴===.
(解法2:整体求解)过图①中菱形的顶点B作BE⊥AD于E,设图②中正八边形的中心点为点O,一边为MN,连结OM、ON,过M点作MP⊥ON于P,设正八边形的边长为a,则AB=AD=MN=a,由正八边形的性质可得∠ABC==135°,∠MON==45°,∵AD∥BC,∴∠BAE=45°,∴BE=AB=a,∴S菱形ABCD=AD·BE=a2,∴空白部分的面积为4×a2=2a2,∵∠MON=45°,MP⊥ON,∴∠OMP=45°=∠MON,∴OP=PM,设OP=PM=x,则OM=ON=x,∴PN=(-1)x,∵PM2+PN2=MN2,∴x2+(-1)2x2=a2,∴x2=a2,
∴S△OMN=ON·PM=x2=a2,∴正八边形的面积为8×a2=2(+1)a2,∴阴影部分的面积为2(+1)a2-2a2=2a2,
∴阴影部分面积与空白部分面积之比为=.
17.证明 ∵∠CAB=∠CBA,∠CAB=∠BOC,∠CBA∠AOC,∴∠AOC=∠BOC,∴AC=BC,∵OA=OB,OC=OC,∴△OAC≌△OBC.
18.解析 设圆锥底面圆的半径为r,∵AC=3,∠ACB=120°,∴的长==2π,∴2πr=2π,∴r=1,即OA=1,∴OC===2,故圆锥的高OC为2.
19.解析 (1)∵☉O是等边三角形ABC的外接圆,∴点O是等边三角形ABC的外心,∴CE⊥AB,∠1=∠2=30°.∴∠ADC=∠BDC=90°,∵AC=BC,CD=CD,
∴Rt△ACD≌Rt△BCD.故答案为∠1(答案不唯一);△BCD.
(2)证明:∵CE为☉O的直径,∴∠CBE=90°,∴∠ADE=∠CBE,∵=,∴∠3=∠2,∴△AED∽△CEB.
(3)四边形OAEB为菱形.
理由:如图,∵∠CAE=90,∠1=30°,∴AE=CE.同理BE=CE,∴OA=OB=AE=BE,∴四边形OAEB为菱形.
20.解析 (1)证明:如图,连结OC,∵OA=OC,∴∠OAC=∠OCA,
∵点C是的中点,∴∠OAC=∠CAE,∴∠CAE=∠OCA,∴OC∥AE,∵AE⊥CE,∴OC⊥CE,∵OC是半径,∴CE是☉O的切线.
(2)∵AB为☉O的直径,∴∠ACB=90°,∵BC=6,AC=8,∴AB==10,
∵∠BAC=∠CAE,∠AEC=∠ACB=90°,∴△AEC∽△ACB,∴=,即=,∴EC=,∵点C是的中点,即=,∴CD=BC=6,∴DE==.
21.解析 (1)证明:如图,连结OP,设BO的延长线与☉O交于点C,则OP=OB=OC,∵AP与☉O相切于点P,∴∠APO=90°,∴∠PAO+∠AOP=90°,∵MO⊥CN,∴∠AOP+∠POC=90°,∴∠PAO=∠POC,∵OP=OB,∴∠OPB=∠PBO,∴∠POC=2∠PBO,∴∠PAO=2∠PBO.
(2)如图,连结PC,过点P作PD⊥OC于点D.在Rt△APO中,AO==,由(1)可知∠POC=∠PAO,∵∠APO=∠PDO=90°,∴△POD∽△OAP,∴==,即==,解得PD=3,OD=4,∴CD=OC-OD=1,在Rt△PDC中,PC==,∵CB为☉O的直径,∴∠BPC=90°,∴BP===3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
第27章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023江苏镇江期中)下列说法正确的是( )
A.弧长相等的弧是等弧
B.直径是最长的弦
C.三点确定一个圆
D.平分弦的直径垂直于弦
2.(2023河南中考)如图,点A,B,C在☉O上,若∠C=55°,则∠AOB的度数为( )
A.95° B.100°
C.105° D.110°
3.(2023四川广元苍溪期末)如图,点P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段OP的长为( )
A.3 B.3
C.6 D.9
4.【易错题】(2023四川泸州泸县模拟)在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆与x轴的位置关系是( )
A.相交 B.相离
C.相切 D.无法判断
5.(2023吉林松原前郭模拟)如图,四边形ABCD内接于☉O,AB是☉O的直径,EF与☉O相切于点A,若∠C=120°,则∠DAE的度数为( )
A.20° B.30° C.50° D.60°
6.【中华优秀传统文化】(2023湖北恩施州巴东期中)扇子最早称“翣”,在我国已有两千多年历史.“打开半个月亮,收起兜里可装,来时荷花初放,去时菊花正黄.”这则谜语说的就是扇子.如图,一竹扇完全打开后,外侧两竹条AB,AC的夹角为135°,AB的长为30 cm,扇面BD的长为
20 cm,则扇面的面积为( )
A.π cm2 B.600π cm2
C.300π cm2 D.30π cm2
7.【中华优秀传统文化】(2023陕西中考)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图2是从正面看到的一个“老碗”(图1)的形状示意图,是☉O的一部分,D是的中点,连结OD,与弦AB交于点C,连结OA,OB.已知AB=24 cm,碗深CD=8 cm,则☉O的半径OA为( )
A.13 cm B.16 cm
C.17 cm D.26 cm
8.【数学文化】【新考向·新定义试题】(2023湖南张家界中考)“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,三段圆弧围成的封闭图形就是“莱洛三角形”.若等边△ABC的边长为3,则该“莱洛三角形”的周长等于( )
A.π B.3π C.2π D.2π-
9.【新考法】(2023河南开封龙亭模拟)如图,☉O的半径为1,AD,BC是☉O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )
10.(2023湖南永州冷水滩京华中学期末)如图,PA、PB是☉O的切线,切点分别为A、B,BC是☉O的直径,PO交☉O于E点,连结AB交PO于F,连结CE交AB于D点,连结AC.下列结论:①PA=PB;②OP⊥AB;③CE平分∠ACB;④OF=AC;⑤E是△PAB的内心;⑥△CDA≌△EDF.其中一定成立的有( )
A.5个 B.4个 C.3个 D.2个
二、填空题(每小题3分,共18分)
11.(2023浙江杭州保俶塔申花实验学校模拟)如图,PA,PB与☉O分别相切于点A,B,PA=3,∠P=60°,则AB= .
12.(2023广东佛山南海平洲二中月考)如图,在☉O中,=,A、C之间的距离为4,则线段BD= .
13.【新独家原创】在☉O的圆周上任意标出三个点A、B、C,然后顺次连结点O、A、B、C得到一个四边形,若∠AOC=∠ABC,则∠ABC= .
14.【教材变式·P55T1】(2023山西晋城阳城模拟)点P是非圆上一点,若点P到☉O上的点的最小距离是4 cm,最大距离是9 cm,则☉O的半径是 .
15.【数学文化】(2023河北保定高碑店模拟)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问积及为米几何 ”译文:屋内墙角处的米堆为一个圆锥的四分之一(如图),米堆底部的弧长为8尺,米堆的高为5尺,那么这个米堆遮挡的墙面面积为 平方尺.
16.【新考法】【一题多解】(2023甘肃天水麦积模拟)由四个图1所示的四边形和四个图2所示的菱形拼成一个正八边形(如图3),则图3中阴影部分面积与空白部分面积之比为 .
三、解答题(共52分)
17.(2023吉林长春经开区模拟)(6分)如图,点A、B、C都在☉O上,∠CAB=∠CBA.
求证:△OAC≌△OBC.
18.(2023安徽安庆怀宁模拟)(8分)如图,圆锥侧面展开得到扇形,此扇形半径CA=3,圆心角∠ACB=120°,求此圆锥的高OC.
19.【新考向·开放性试题】(2023贵州中考)(12分)如图,已知☉O是等边三角形ABC的外接圆,连结CO并延长交AB于点D,交☉O于点E,连结EA,EB.
(1)写出图中一个度数为30°的角: ,图中与△ACD全等的三角形是 ;
(2)求证:△AED∽△CEB;
(3)连结OA,OB,判断四边形OAEB的形状,并说明理由.
20.(2023湖南常德中考)(12分)如图,四边形ABCD是☉O的内接四边形,AB是直径,C是的中点,过点C作CE⊥AD交AD的延长线于点E.
(1)求证:CE是☉O的切线;
(2)若BC=6,AC=8,求CE,DE的长.
21.【跨学科·物理】(14分)在古代,智慧的劳动人民已经会使用“石磨”(如图),其原理为在磨盘的边缘连结一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图1所示,两个固定长度的“连杆”AP,BP的连结点P在☉O上,当点P在☉O上转动时,带动点A,B分别在射线OM,ON上滑动,OM⊥ON.当AP与☉O相切时,点B恰好落在☉O上,如图2.
根据图2解答下列问题.
(1)求证:∠PAO=2∠PBO;
(2)若☉O的半径为5,AP=,求BP的长.
图1
图2
答案全解全析
1.B 能够重合的弧是等弧,故选项A说法错误;不在同一条直线上的三点确定一个圆,故选项C说法错误;平分弦(不是直径)的直径垂直于弦,故选项D说法错误.
2.D ∵∠AOB=2∠C,∠C=55°,∴∠AOB=110°.
3.C 如图,连结OA,∵PA为☉O的切线,∴∠OAP=90°,∵OB=3,∴AO=OB=3,∵∠P=30°,∴OP=2OA=6.
4.C 确定圆心与x轴的距离时易因弄错数据致错.∵圆心的坐标为
(-3,4),∴圆心与x轴距离为4,等于其半径4,∴以点(-3,4)为圆心,4为半径的圆与x轴的位置关系为相切.
5.B ∵四边形ABCD内接于☉O,∴∠C+∠DAB=180°,∵∠C=120°,∴∠DAB=60°,∵EF与☉O相切于点A,∴OA⊥EF,∴∠OAE=90°,∴∠DAE=∠OAE-∠DAB=30°.
6.C ∵AB=30 cm,BD=20 cm,∴AD=10 cm,∵∠BAC=135°,∴扇面的面积=-=-=300π(cm2).
7.A ∵是☉O的一部分,D是的中点,AB=24 cm,∴OD⊥AB,AC=BC=AB=12 cm.设☉O的半径OA为R cm,则OC=OD-CD=(R-8)cm.在Rt△OAC中,OA2=AC2+OC2,∴R2=122+(R-8)2,∴R=13,即☉O的半径OA为13 cm.
8.B ∵△ABC是等边三角形,∴AB=BC=AC=3,∠A=∠B=∠C=60°,∴==,∵的长==π,∴该“莱洛三角形”的周长是3π.
9.C 本题将函数图象与圆的性质融为一体考查,设计新颖.当P在OC上运动时,根据题意得sin∠APB=,∵OA=1,AP=x,y=sin∠APB,∴y=(1
AF=BF,∴OF=AC,故④正确;∵PB是☉O的切线,∴∠PBE+∠EBC=90°,∵BC是☉O的直径,∴∠BEC=90°,∴∠EBC+∠ECB=90°,∴∠PBE=∠ECB,∵=,
∴∠ECB=∠EBA,∴∠PBE=∠EBA,∵∠APE=∠BPE,∴E是△PAB的内心,故⑤正确;∵AC∥OE,∴△CDA∽△EDF,故⑥错误.故选A.
11.3
解析 ∵PA,PB分别与☉O相切于点A,B,∴PA=PB,∵∠P=60°,∴△PAB是等边三角形,∴AB=PA=3.
12.4
解析 如图,连结BD,AC.∵=,∴+=+,∴=,∴BD=AC=4.
13.120°
解析 如图,在优弧AC上任取一点D,连结AD、CD,∵四边形ADCB是☉O的内接四边形,∴∠ADC+∠ABC=180°,∠ADC=∠AOC,∵∠AOC=∠ABC,
∴∠ADC=∠ABC,∴∠ABC+∠ABC=180°,∴∠ABC=120°.
14.6.5 cm或2.5 cm
解析 分两种情况讨论:
(1)当点在圆内时,如图1,∵点到圆上的点的最小距离PB=4 cm,最大距离PA=9 cm,∴直径AB=4+9=13(cm),∴半径为6.5 cm;
(2)当点在圆外时,如图2,∵点到圆上的最小距离PB=4 cm,最大距离PA=9 cm,∴直径AB=9-4=5(cm),∴半径为2.5 cm.
综上所述,圆O的半径为6.5 cm或2.5 cm.
15.
解析 设圆锥的底面半径为r尺,由米堆底部的弧长为8尺可得×2πr=8,解得r=,∴2×××5=(平方尺),∴这个米堆遮挡的墙面面积为平方尺.
16.
解析 本题将菱形和正多边形融合在一起,考查综合运用数学知识解决问题的能力.(解法1:局部求解)如图,正八边形的每个内角的度数为×(8-2)×180°=135°,∴∠ABC=∠BAP=135°,∴∠BAD=∠PAE=45°,
∴∠DAE=45°.在△ABD和△ADE中,∵AB=AD,∠BAD=∠DAE,AD=AE,∴△ABD≌△ADE,∴BD=DE,
∴DF=BD=DE=DG.由对称性易知四边形DEMN为正方形,∴OD=DG=DF.设S△CDF=a,则=4a,S△OCD=a,∴===.
(解法2:整体求解)过图①中菱形的顶点B作BE⊥AD于E,设图②中正八边形的中心点为点O,一边为MN,连结OM、ON,过M点作MP⊥ON于P,设正八边形的边长为a,则AB=AD=MN=a,由正八边形的性质可得∠ABC==135°,∠MON==45°,∵AD∥BC,∴∠BAE=45°,∴BE=AB=a,∴S菱形ABCD=AD·BE=a2,∴空白部分的面积为4×a2=2a2,∵∠MON=45°,MP⊥ON,∴∠OMP=45°=∠MON,∴OP=PM,设OP=PM=x,则OM=ON=x,∴PN=(-1)x,∵PM2+PN2=MN2,∴x2+(-1)2x2=a2,∴x2=a2,
∴S△OMN=ON·PM=x2=a2,∴正八边形的面积为8×a2=2(+1)a2,∴阴影部分的面积为2(+1)a2-2a2=2a2,
∴阴影部分面积与空白部分面积之比为=.
17.证明 ∵∠CAB=∠CBA,∠CAB=∠BOC,∠CBA∠AOC,∴∠AOC=∠BOC,∴AC=BC,∵OA=OB,OC=OC,∴△OAC≌△OBC.
18.解析 设圆锥底面圆的半径为r,∵AC=3,∠ACB=120°,∴的长==2π,∴2πr=2π,∴r=1,即OA=1,∴OC===2,故圆锥的高OC为2.
19.解析 (1)∵☉O是等边三角形ABC的外接圆,∴点O是等边三角形ABC的外心,∴CE⊥AB,∠1=∠2=30°.∴∠ADC=∠BDC=90°,∵AC=BC,CD=CD,
∴Rt△ACD≌Rt△BCD.故答案为∠1(答案不唯一);△BCD.
(2)证明:∵CE为☉O的直径,∴∠CBE=90°,∴∠ADE=∠CBE,∵=,∴∠3=∠2,∴△AED∽△CEB.
(3)四边形OAEB为菱形.
理由:如图,∵∠CAE=90,∠1=30°,∴AE=CE.同理BE=CE,∴OA=OB=AE=BE,∴四边形OAEB为菱形.
20.解析 (1)证明:如图,连结OC,∵OA=OC,∴∠OAC=∠OCA,
∵点C是的中点,∴∠OAC=∠CAE,∴∠CAE=∠OCA,∴OC∥AE,∵AE⊥CE,∴OC⊥CE,∵OC是半径,∴CE是☉O的切线.
(2)∵AB为☉O的直径,∴∠ACB=90°,∵BC=6,AC=8,∴AB==10,
∵∠BAC=∠CAE,∠AEC=∠ACB=90°,∴△AEC∽△ACB,∴=,即=,∴EC=,∵点C是的中点,即=,∴CD=BC=6,∴DE==.
21.解析 (1)证明:如图,连结OP,设BO的延长线与☉O交于点C,则OP=OB=OC,∵AP与☉O相切于点P,∴∠APO=90°,∴∠PAO+∠AOP=90°,∵MO⊥CN,∴∠AOP+∠POC=90°,∴∠PAO=∠POC,∵OP=OB,∴∠OPB=∠PBO,∴∠POC=2∠PBO,∴∠PAO=2∠PBO.
(2)如图,连结PC,过点P作PD⊥OC于点D.在Rt△APO中,AO==,由(1)可知∠POC=∠PAO,∵∠APO=∠PDO=90°,∴△POD∽△OAP,∴==,即==,解得PD=3,OD=4,∴CD=OC-OD=1,在Rt△PDC中,PC==,∵CB为☉O的直径,∴∠BPC=90°,∴BP===3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
