2024华东师大版数学九年级下学期课时练--期末素养综合测试(二)(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--期末素养综合测试(二)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 681.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 20:44:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
期末素养综合测试(二)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.党的二十大报告提出“深化全民阅读活动”.某校开展了“书香浸润心灵,阅读点亮人生”读书系列活动.为了解学生的课外阅读情况,从全校2 000名学生记录的一周的课外阅读时间(单位:小时)中随机抽取了200名学生一周的课外阅读时间(单位:小时)进行统计,在这个问题中以下说法正确的是( )
A.200名学生一周的课外阅读时间是样本
B.200名学生是总体
C.此调查为全面调查
D.样本容量是2 000
2.(2023湖南衡阳中考)对于二次根式的乘法运算,一般地,有·=.该运算法则成立的条件是( )
A.a>0,b>0 B.a<0,b<0
C.a≤0,b≤0 D.a≥0,b≥0
3.(2023黑龙江牡丹江中考)如图,A,B,C为☉O上的三个点,∠AOB=4∠BOC,若∠ACB=60°,则∠BAC的度数是( )
A.20° B.18° C.15° D.12°
4.(2023重庆渝中巴蜀中学期末)如图所示的是一次函数y=kx+b的图象,则二次函数y=kx2+bx+2的图象可能为( )
5.(2023吉林长春绿园模拟)图1是等边三角形铁丝框ABC,变形成图2所示的以A为圆心,AB长为半径的扇形(图形周长保持不变),则所得扇形ABC的圆心角的度数是( )
A.45° B.60° C. D.
6.【新考向·新定义试题】(2023四川内江中考)对于实数a,b定义运算“ ”为a b=b2-ab,例如:3 2=22-3×2=-2,则关于x的方程(k-3) x=k-1的根的情况,下列说法正确的是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
7.【中华优秀传统文化】(2023湖南株洲模拟)“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是( )
A. B. C. D.
8.【新考法】(2023山东日照模拟)如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,将△OAB缩小为原来的得到△OA1B1,当反比例函数y=(k≠0)的图象经过A1B1的中点时,k的值为( )
A.30 B.
C.30或-30 D.或-
9.(2023黑龙江牡丹江中考)如图,抛物线y=ax2+bx+c经过点(-2,0),(3,0).下列结论:①>0;②c=2b;③若抛物线上有点,(-3,y2),,则y2A.4 B.3 C.2 D.1
10.(2023河南洛阳模拟)如图,抛物线y=x2-x-与x轴交于点A,B,与y轴交于点C,顶点为D,以AB为直径在x轴上方画半圆交y轴于点E,圆心为I,P是半圆上一动点,连结DP,点Q为PD的中点,连结IQ.下列四种说法:
①点C在☉I上;
②IQ⊥PD;
③当点P沿半圆从点B运动至点A时,点Q运动的路径长为π;
④线段BQ的长可以是3.2.
其中正确说法的个数为( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共24分)
11.【易错题】(2023四川广元中考)若式子有意义,则实数x的取值范围是 .
12.(2023四川眉山中考)已知方程x2-3x-4=0的根为x1,x2,则(x1+2)·(x2+2)的值为 .
13.(2023浙江金华模拟)已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,且经过点(-1,y1),(2,y2),试比较y1和y2的大小:y1 y2.(填“>”“<”或“=”)
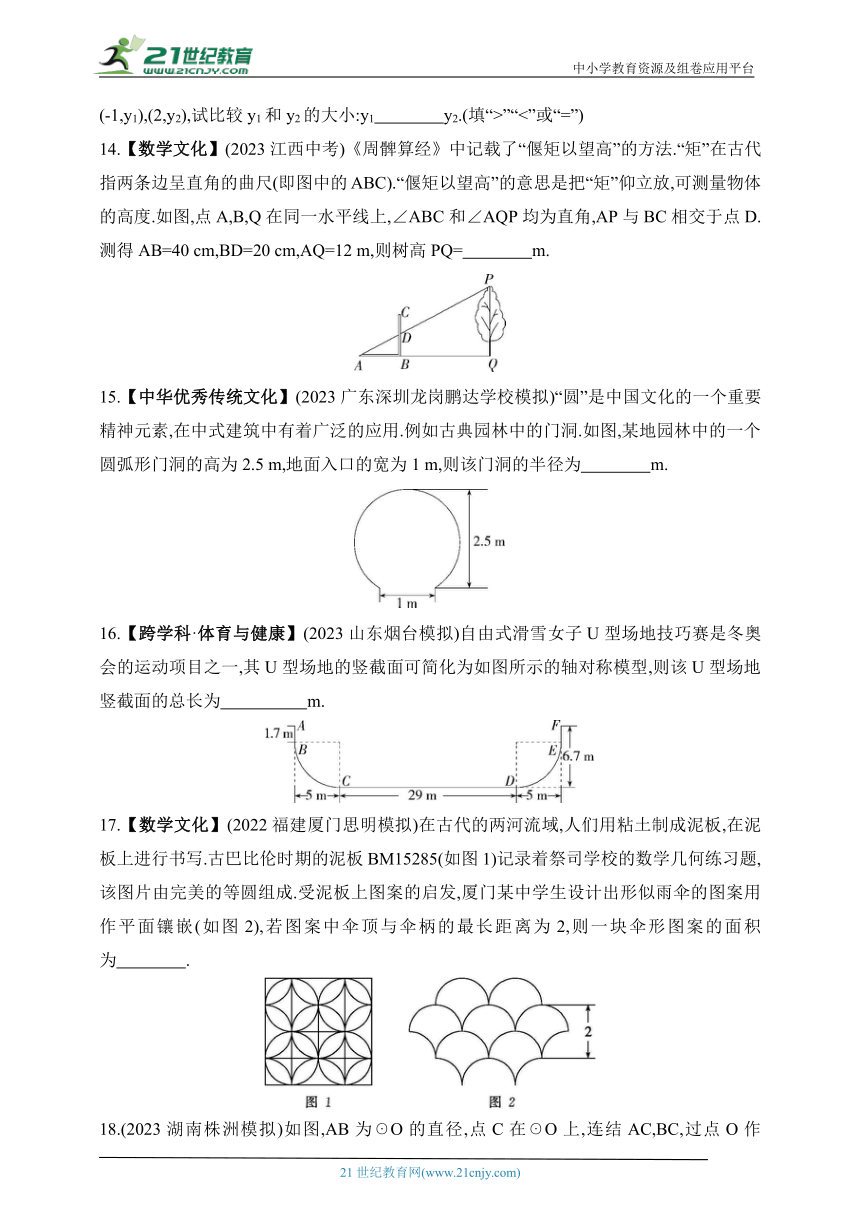
14.【数学文化】(2023江西中考)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,∠ABC和∠AQP均为直角,AP与BC相交于点D.测得AB=40 cm,BD=20 cm,AQ=12 m,则树高PQ= m.
15.【中华优秀传统文化】(2023广东深圳龙岗鹏达学校模拟)“圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的应用.例如古典园林中的门洞.如图,某地园林中的一个圆弧形门洞的高为2.5 m,地面入口的宽为1 m,则该门洞的半径为 m.
16.【跨学科·体育与健康】(2023山东烟台模拟)自由式滑雪女子U型场地技巧赛是冬奥会的运动项目之一,其U型场地的竖截面可简化为如图所示的轴对称模型,则该U型场地竖截面的总长为 m.
17.【数学文化】(2022福建厦门思明模拟)在古代的两河流域,人们用粘土制成泥板,在泥板上进行书写.古巴比伦时期的泥板BM15285(如图1)记录着祭司学校的数学几何练习题,该图片由完美的等圆组成.受泥板上图案的启发,厦门某中学生设计出形似雨伞的图案用作平面镶嵌(如图2),若图案中伞顶与伞柄的最长距离为2,则一块伞形图案的面积为 .
18.(2023湖南株洲模拟)如图,AB为☉O的直径,点C在☉O上,连结AC,BC,过点O作OD⊥BC于点D,过点C作☉O的切线交OD的延长线于点E,连结AD,若CE=4,BC=8,则AD的长为 .
三、解答题(共66分)
19.[含评分细则]【中华优秀传统文化】(2023浙江金华东阳江北初级中学期末)(8分)澄泥砚是中国四大名砚之一,其历史可上溯到唐代,为陶砚,以泥沙再造而成,其质细腻,柔中有坚,贮水不涸,历寒不冰,发墨护毫,兼具陶石双重优点,某电商直播销售一款澄泥砚,每块澄泥砚的成本为30元,当每块售价定为48元时,平均每月可售出500块澄泥砚,通过市场调查发现,若销售单价每上涨1元,其月销售量就减少10块,若想销售澄泥砚的月利润恰好为11 200元,且每块售价上涨不超过20元,则每块澄泥砚的售价应上涨多少元
20.[含评分细则]【项目式学习试题】(2023吉林中考)(10分)某校数学活动小组要测量校园内一棵古树的高度,王朵同学带领小组成员进行此项实践活动,记录如下:
综合实践活动报告
填写人:王朵 时间:2023年4月20日
活动任务:测量古树高度
活动过程
【步骤一】设计测量方案 小组成员讨论后,画出如图①所示的测量草图,确定需测的几何量
【步骤二】准备测量工具 自制测角仪,把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角,如图②所示. 准备皮尺
【步骤三】实地测量并记录数据 如图③,王朵同学站在离古树一定距离的地方,将这个测角仪用手托起,拿到眼前,使视线沿着测角仪的直径刚好到达古树的最高点. 如图④,利用测角仪,测量后计算得出仰角α= . 测出眼睛到地面的距离AB=1.54 m. 测出所站地方到古树底部的距离BD=10 m
【步骤四】计算古树高度CD(结果精确到0.1 m) (参考数据:sin 40°≈0.643,cos 40°≈0.766,tan 40°≈0.839)
请结合图①、图④和相关数据写出α的度数并完成【步骤四】.
21.[含评分细则]【革命文化】(2023甘肃武威中考)(10分)为传承红色文化,激发革命精神,增强爱国主义情感,某校组织七年级学生开展以“讲好红色故事,传承红色基因”为主题的研学之旅,策划了三条红色线路让学生选择:
A.南梁精神红色记忆之旅(华池县);B.长征会师胜利之旅(会宁县);C.西路军红色征程之旅(高台县),且每人只能选择一条线路.小亮和小刚两人用抽卡片的方式确定一条自己要去的线路.他们准备了3张不透明的卡片,正面分别写上字母A,B,C,卡片除正面字母不同外其余均相同,将3张卡片正面向下洗匀,小亮先从中随机抽取一张卡片,记下字母后正面向下放回,洗匀后小刚再从中随机抽取一张卡片.
(1)求小亮从中随机抽到卡片A的概率;
(2)请用画树状图或列表的方法,求两人都抽到卡片C的概率.
22.[含评分细则](2023湖南张家界中考)(12分)阅读下面材料:
将边长分别为a,a+,a+2,a+3的正方形面积分别记为S1,S2,S3,S4,则S2-S1=(a+)2-a2=[(a+)+a]·[(a+)-a]=(2a+)·=b+2a.例如:当a=1,b=3时,S2-S1=3+2.
根据以上材料,解答下列问题:
(1)当a=1,b=3时,S3-S2= ,S4-S3= ;
(2)当a=1,b=3时,把边长为a+n的正方形的面积记作,其中n是正整数,从(1)中的计算结果,你能猜出-Sn等于多少吗 并证明你的猜想;
(3)当a=1,b=3时,令t1=S2-S1,t2=S3-S2,t3=S4-S3,……,tn=-Sn,且T=t1+t2+t3+…+t50,求T的值.
23.[含评分细则](2023吉林长春中考)(12分)【感知】如图1,点A、B、P均在☉O上,∠AOB=90°,则锐角∠APB的大小为 度.
【探究】小明遇到这样一个问题:如图2,☉O是等边三角形ABC的外接圆,点P在上(点P不与点A、C重合),连结PA、PB、PC.求证:PB=PA+PC.小明发现,延长PA至点E,使AE=PC,连结BE,通过证明△PBC≌△EBA,可推得△PBE是等边三角形,进而得证.下面是小明的部分证明过程:
证明:延长PA至点E,使AE=PC,连结BE.
∵四边形ABCP是☉O的内接四边形,
∴∠BAP+∠BCP=180°,
∵∠BAP+∠BAE=180°,∴∠BCP=∠BAE,
∵△ABC是等边三角形,∴BA=BC,
∴△PBC≌△EBA.
请你补全余下的证明过程.
【应用】如图3,☉O是△ABC的外接圆,∠ABC=90°,AB=BC,点P在☉O上,且点P与点B在AC的两侧,连结PA、PB、PC,若PB=2PA,则的值为 .
24.[含评分细则](2023吉林长春中考)(14分)在平面直角坐标系中,点O为坐标原点,抛物线y=-x2+bx+2(b是常数)经过点(2,2),点A的坐标为(m,0),点B在该抛物线上,横坐标为1-m,其中m<0.
(1)求该抛物线对应的函数表达式及顶点坐标;
(2)当点B在x轴上时,求点A的坐标;
(3)该抛物线与x轴的左交点为P,当抛物线在点P和点B之间的部分(包括P,B两点)的最高点与最低点的纵坐标之差为2-m时,求m的值;
(4)当点B在x轴上方时,过点B作BC⊥y轴于点C,连结AC、BO.若四边形AOBC的边和抛物线有两个交点(不包括四边形AOBC的顶点),设这两个交点分别为点E、点F,线段BO的中点为D.当以点C、E、O、D(或点C、F、O、D)为顶点的四边形的面积是四边形AOBC面积的一半时,直接写出所有满足条件的m的值.
答案全解全析
1.A 2 000名学生一周的课外阅读时间是总体,此调查为抽样调查,样本容量是200.
2.D 对于二次根式的乘法运算,一般地,有·=.该运算法则成立的条件是a≥0,b≥0.
3.C ∵∠ACB=60°,∴∠AOB=2∠ACB=120°,∵∠AOB=4∠BOC,∴∠BOC=30°,∴∠BAC=∠BOC=15°.
4.C 由一次函数y=kx+b的图象可得k>0,b>0,∴二次函数y=kx2+bx+2的图象开口向上,对称轴为直线x=-<0.故选C.
5.D 设AB=BC=x,扇形圆心角度数为n°,∴=x,解得n=,∴圆心角的度数为.
6.A ∵(k-3) x=k-1,∴x2-(k-3)x=k-1,∴x2-(k-3)x-k+1=0,∴Δ=[-(k-3)]2-4×1×(-k+1)=(k-1)2+4>0,∴关于x的方程(k-3) x=k-1有两个不相等的实数根.
7.C 设“立春”用A表示,“立夏”用B表示,“秋分”用C表示,“大寒”用D表示,画树状图如下,
由上可得一共有12种等可能的结果,其中小乐抽到的两张邮票恰好是“立春”和“立夏”的有2种,∴小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是=.
8.B 本题将位似与反比例函数融为一体考查,体现了数学学科的综合性.∵以原点O为位似中心,将△OAB缩小为原来的得到△OA1B1,A(2,4),B(4,1),∴A1(-1,-2),B1或A1(1,2),B1,∴A1B1的中点坐标为或,代入y=得k=-×=或k=×=.
9.D ∵抛物线开口向下,与y轴交于正半轴,对称轴在y轴右侧,∴a<0,b>0,c>0,∴<0,故①错误;∵抛物线y=ax2+bx+c经过点(-2,0),(3,0),∴对称轴为直线x=,即-=,∴a=-b,把(-2,0)代入解析式得4a-2b+c=0,∵a=-b,∴-4b-2b+c=0,∴c=6b,故②错误;∵抛物线开口向下,∴越靠近对称轴的点的纵坐标越大,∴y210.B 抛物线y=x2-x-与坐标轴交于点A,B,C,∴A(-1,0),B(3,0),C,∴AB=4,∴I(1,0),☉I的半径为2,连结ID、IC(图略),∵y=x2-x-=(x-1)2-2,∴顶点D的坐标为(1,-2),∴ID=2,∴点D在☉I上,∵IC===≠2,∴点C不在☉I上,故①不正确;
∵圆心为I,P是半圆上一动点,点D在☉I上,点Q为PD的中点,∴IQ⊥PD,故②正确;
如图,点G、Q、I、F是点Q运动中所处的位置,则GF是等腰直角三角形ABD的中位线,∴GF=AB=2,设ID交GF于点R,易知四边形GDFI为正方形,IQ⊥PD,连结QR,则QR=ID=IR=RD=RG=RF=GF=1,则点Q的运动轨迹为以R为圆心,1为半径的半圆,则点Q运动的路径长=×2π×1=π,故③正确;
由③知当点Q运动到点G的位置时,BQ的长最大,最大值为=<3.2,∴线段BQ的长不可以是3.2,故④不正确.
综上所述,正确的说法为②③,共2个.
11.x>3
解析 本题易忽略二次根式在分母的位置而致错,由题意得x-3>0,解得x>3.
12.6
解析 ∵方程x2-3x-4=0的根为x1,x2,∴x1+x2=3,x1·x2=-4,∴(x1+2)·(x2+2)=x1·x2+2x1+2x2+4=x1·x2+2(x1+x2)+4=-4+2×3+4=6.
13.>
解析 ∵二次函数y=ax2+bx+c(a>0)的图象开口向上,对称轴为直线x=1,∴越靠近对称轴的点的纵坐标y越小,∵1-(-1)=2,2-1=1,∴点(-1,y1)离对称轴的距离比点(2,y2)要远,∴y1>y2.
14.6
解析 由题意可得BC∥PQ,∴△ABD∽△AQP,∴=,即=,∴QP=6 m,∴树高PQ=6 m.
15.1.3
解析 设该门洞的半径为r m,圆心为O,连结CD、OC、OD,过O作EF⊥CD于F,交☉O于点E,则DF=CD= m,EF=r+OF=2.5 m,在Rt△OFD中,OF=,所以+r=2.5,解得r=1.3.故该门洞的半径为1.3 m.
16.(5π+32.4)
解析 竖截面的总长=AB++CD++EF=1.7+×2+29+6.7-5=(5π+32.4)m.
17.2
解析 如图,观察可知一块伞形图案的面积=正方形ABCD的面积=×2×2=2.
18.4
解析 如图,连结OC,∵EC是☉O的切线,∴∠OCE=90°,∵OD⊥BC,∴∠EDC=90°,∴∠OCD+∠ECD=∠E+∠ECD=90°,
∴∠OCD=∠E,∵OB=OC,∴∠OCD=∠B,∴∠E=∠B.∵OD⊥BC,OB=OC,
∴BD=CD=BC=4,∴DE==8,∴BC=DE,∵AB为☉O的直径,∴∠ACB=90°,∴∠ACB=∠CDE,又∵∠B=∠E,∴△ACB≌△CDE,∴AC=CD=4,∴AD==4.
19.解析 设每块澄泥砚的售价应上涨x元,则每块的销售利润为(48+x-30)元,平均每月可售出(500-10x)块,根据题意得(48+x-30)(500-10x)=11 200,整理得x2-32x+220=0,5分
解得x1=10,x2=22(不符合题意,舍去).
答:每块澄泥砚的售价应上涨10元.8分
20.解析 测角仪显示的度数为50°,∴α=90°-50°=40°,由题图①可知AB⊥BD,ED⊥BD,CE⊥AE,∴∠ABD=∠EDB=∠AED=90°,∴四边形ABDE是矩形,4分
∴AE=BD=10 m,ED=AB=1.54 m,6分
在Rt△CAE中,CE=AE·tan α≈10×0.839=8.39(m),∴CD=CE+ED=8.39+1.54=9.93≈9.9(m),即古树高度CD约为9.9 m.10分
21.解析 (1)小亮从中随机抽到卡片A的概率为.3分
(2)画树状图如下,
7分
由图可知共有9种等可能的结果,其中小亮和小刚两人都抽到卡片C的结果有1种,∴两人都抽到卡片C的概率是.10分
22.解析 (1)S3-S2=(a+2)2-(a+)2=a2+4a+4b-a2-2a-b=2a+3b,当a=1,b=3时,S3-S2=9+2.2分
S4-S3=(a+3)2-(a+2)2=a2+6a+9b-a2-4a-4b=2a+5b,当a=1,b=3时,S4-S3=15+2.4分
(2)-Sn=6n-3+2.5分
证明如下:由题目和(1)知,当a=1,b=3时,
S2-S1=(1+)2-12=3+2,
S3-S2=(1+2)2-(1+)2=9+2,
S4-S3=(1+3)2-(1+2)2=15+2,
……
∴Sn+1-Sn=(1+n)2-[1+(n-1)]2=6n-3+2.8分
(3)当a=1,b=3时,T=t1+t2+t3+…+t50=S2-S1+S3-S2+S4-S3+…+S51-S50=S51-S1=(1+50)2-12=7 500+100.12分
23.解析 【感知】∵∠AOB=90°,
∴∠APB=∠AOB=45°.3分
【探究】证明:延长PA至点E,使AE=PC,连结BE.
∵四边形ABCP是☉O的内接四边形,
∴∠BAP+∠BCP=180°,
∵∠BAP+∠BAE=180°,∴∠BCP=∠BAE,
∵△ABC是等边三角形,∴BA=BC,
∴△PBC≌△EBA.
∴PB=EB,∵△ABC是等边三角形,∴∠ACB=60°,∴∠APB=60°,∴△PBE为等边三角形,∴PB=PE=AP+AE=PA+PC.8分
【应用】如图,延长PA至点G,使AG=PC,连结BG.∵四边形ABCP是☉O的内接四边形,∴∠BAP+∠BCP=180°,∵∠BAP+∠BAG=180°,∴∠BCP=∠BAG,∵BA=BC,
∴△PBC≌△GBA,∴PB=GB,∠PBC=∠GBA,∵∠ABC=90°,∴∠PBG=∠GBA+∠ABP=∠PBC+∠ABP=∠ABC=90°,∴PG=BP=4PA,
∵PG=PA+AG=PA+PC,∴PC=PG-PA=4PA-PA=3PA,∴==.12分
24.解析 (1)将点(2,2)代入抛物线y=-x2+bx+2中得2=-4+2b+2,解得b=2,∴抛物线的解析式为y=-x2+2x+2=-(x-1)2+3,∴顶点坐标为(1,3).2分
(2)当y=0时,-x2+2x+2=0,解得x1=1-,x2=1+,∵点B的横坐标为1-m,其中m<0,∴1-m>1,∴1-m=1+,解得m=-,∵点A的坐标为(m,0),∴A(-,0).4分
(3)由(2)知,P(1-,0),∵m<0,∴1-m>1,∴点B一定在对称轴右侧,∴B(1-m,-m2+3),5分
分情况求解如下:
①如图a所示,当1<1-m<1+,即-②如图b所示,当1-m≥1+,即m≤-时,依题意得3-(-m2+3)=2-m,解得m=-2或m=1(舍去).7分
综上所述,m=-1或m=-2.
(4)如图1所示,连结CD,∵B在x轴的上方,∴1-<1-m<1+且m<0,∴-分情况求解如下:
①当E是AC的中点,即E时,如图2,连结OE,则S△AOE=S△COE,此时S四边形AOBC=S四边形CEOD,将E代入y=-x2+2x+2,得=-+2×+2,解得m=--2(舍去)或m=-2+;10分
②同理当F为AO的中点,即F时,如图3所示,连结CF,则S△ACF=S△CFO,此时S四边形AOBC=S四边形CFOD,∴=1-,解得m=2-2;12分
③如图4所示,连结DF,∵以点C、F、O、D为顶点的四边形的面积是四边形AOBC面积的一半,∴S△COD+S△CFD=S四边形AOBC=(S△AOC+S△BCO),∵S△BCD=S△COD,∴S△CFD=S△AOC,∵D为OB的中点,∴CF=OA,∴F(-m,-m2+3),∵B,F关于直线x=1对称,∴=1,解得m=-.14分
综上所述,m=-2+或m=2-2或m=-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
期末素养综合测试(二)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.党的二十大报告提出“深化全民阅读活动”.某校开展了“书香浸润心灵,阅读点亮人生”读书系列活动.为了解学生的课外阅读情况,从全校2 000名学生记录的一周的课外阅读时间(单位:小时)中随机抽取了200名学生一周的课外阅读时间(单位:小时)进行统计,在这个问题中以下说法正确的是( )
A.200名学生一周的课外阅读时间是样本
B.200名学生是总体
C.此调查为全面调查
D.样本容量是2 000
2.(2023湖南衡阳中考)对于二次根式的乘法运算,一般地,有·=.该运算法则成立的条件是( )
A.a>0,b>0 B.a<0,b<0
C.a≤0,b≤0 D.a≥0,b≥0
3.(2023黑龙江牡丹江中考)如图,A,B,C为☉O上的三个点,∠AOB=4∠BOC,若∠ACB=60°,则∠BAC的度数是( )
A.20° B.18° C.15° D.12°
4.(2023重庆渝中巴蜀中学期末)如图所示的是一次函数y=kx+b的图象,则二次函数y=kx2+bx+2的图象可能为( )
5.(2023吉林长春绿园模拟)图1是等边三角形铁丝框ABC,变形成图2所示的以A为圆心,AB长为半径的扇形(图形周长保持不变),则所得扇形ABC的圆心角的度数是( )
A.45° B.60° C. D.
6.【新考向·新定义试题】(2023四川内江中考)对于实数a,b定义运算“ ”为a b=b2-ab,例如:3 2=22-3×2=-2,则关于x的方程(k-3) x=k-1的根的情况,下列说法正确的是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
7.【中华优秀传统文化】(2023湖南株洲模拟)“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是( )
A. B. C. D.
8.【新考法】(2023山东日照模拟)如图,在平面直角坐标系中,已知点A(2,4),B(4,1),以原点O为位似中心,将△OAB缩小为原来的得到△OA1B1,当反比例函数y=(k≠0)的图象经过A1B1的中点时,k的值为( )
A.30 B.
C.30或-30 D.或-
9.(2023黑龙江牡丹江中考)如图,抛物线y=ax2+bx+c经过点(-2,0),(3,0).下列结论:①>0;②c=2b;③若抛物线上有点,(-3,y2),,则y2
10.(2023河南洛阳模拟)如图,抛物线y=x2-x-与x轴交于点A,B,与y轴交于点C,顶点为D,以AB为直径在x轴上方画半圆交y轴于点E,圆心为I,P是半圆上一动点,连结DP,点Q为PD的中点,连结IQ.下列四种说法:
①点C在☉I上;
②IQ⊥PD;
③当点P沿半圆从点B运动至点A时,点Q运动的路径长为π;
④线段BQ的长可以是3.2.
其中正确说法的个数为( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共24分)
11.【易错题】(2023四川广元中考)若式子有意义,则实数x的取值范围是 .
12.(2023四川眉山中考)已知方程x2-3x-4=0的根为x1,x2,则(x1+2)·(x2+2)的值为 .
13.(2023浙江金华模拟)已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,且经过点(-1,y1),(2,y2),试比较y1和y2的大小:y1 y2.(填“>”“<”或“=”)
14.【数学文化】(2023江西中考)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,∠ABC和∠AQP均为直角,AP与BC相交于点D.测得AB=40 cm,BD=20 cm,AQ=12 m,则树高PQ= m.
15.【中华优秀传统文化】(2023广东深圳龙岗鹏达学校模拟)“圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的应用.例如古典园林中的门洞.如图,某地园林中的一个圆弧形门洞的高为2.5 m,地面入口的宽为1 m,则该门洞的半径为 m.
16.【跨学科·体育与健康】(2023山东烟台模拟)自由式滑雪女子U型场地技巧赛是冬奥会的运动项目之一,其U型场地的竖截面可简化为如图所示的轴对称模型,则该U型场地竖截面的总长为 m.
17.【数学文化】(2022福建厦门思明模拟)在古代的两河流域,人们用粘土制成泥板,在泥板上进行书写.古巴比伦时期的泥板BM15285(如图1)记录着祭司学校的数学几何练习题,该图片由完美的等圆组成.受泥板上图案的启发,厦门某中学生设计出形似雨伞的图案用作平面镶嵌(如图2),若图案中伞顶与伞柄的最长距离为2,则一块伞形图案的面积为 .
18.(2023湖南株洲模拟)如图,AB为☉O的直径,点C在☉O上,连结AC,BC,过点O作OD⊥BC于点D,过点C作☉O的切线交OD的延长线于点E,连结AD,若CE=4,BC=8,则AD的长为 .
三、解答题(共66分)
19.[含评分细则]【中华优秀传统文化】(2023浙江金华东阳江北初级中学期末)(8分)澄泥砚是中国四大名砚之一,其历史可上溯到唐代,为陶砚,以泥沙再造而成,其质细腻,柔中有坚,贮水不涸,历寒不冰,发墨护毫,兼具陶石双重优点,某电商直播销售一款澄泥砚,每块澄泥砚的成本为30元,当每块售价定为48元时,平均每月可售出500块澄泥砚,通过市场调查发现,若销售单价每上涨1元,其月销售量就减少10块,若想销售澄泥砚的月利润恰好为11 200元,且每块售价上涨不超过20元,则每块澄泥砚的售价应上涨多少元
20.[含评分细则]【项目式学习试题】(2023吉林中考)(10分)某校数学活动小组要测量校园内一棵古树的高度,王朵同学带领小组成员进行此项实践活动,记录如下:
综合实践活动报告
填写人:王朵 时间:2023年4月20日
活动任务:测量古树高度
活动过程
【步骤一】设计测量方案 小组成员讨论后,画出如图①所示的测量草图,确定需测的几何量
【步骤二】准备测量工具 自制测角仪,把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角,如图②所示. 准备皮尺
【步骤三】实地测量并记录数据 如图③,王朵同学站在离古树一定距离的地方,将这个测角仪用手托起,拿到眼前,使视线沿着测角仪的直径刚好到达古树的最高点. 如图④,利用测角仪,测量后计算得出仰角α= . 测出眼睛到地面的距离AB=1.54 m. 测出所站地方到古树底部的距离BD=10 m
【步骤四】计算古树高度CD(结果精确到0.1 m) (参考数据:sin 40°≈0.643,cos 40°≈0.766,tan 40°≈0.839)
请结合图①、图④和相关数据写出α的度数并完成【步骤四】.
21.[含评分细则]【革命文化】(2023甘肃武威中考)(10分)为传承红色文化,激发革命精神,增强爱国主义情感,某校组织七年级学生开展以“讲好红色故事,传承红色基因”为主题的研学之旅,策划了三条红色线路让学生选择:
A.南梁精神红色记忆之旅(华池县);B.长征会师胜利之旅(会宁县);C.西路军红色征程之旅(高台县),且每人只能选择一条线路.小亮和小刚两人用抽卡片的方式确定一条自己要去的线路.他们准备了3张不透明的卡片,正面分别写上字母A,B,C,卡片除正面字母不同外其余均相同,将3张卡片正面向下洗匀,小亮先从中随机抽取一张卡片,记下字母后正面向下放回,洗匀后小刚再从中随机抽取一张卡片.
(1)求小亮从中随机抽到卡片A的概率;
(2)请用画树状图或列表的方法,求两人都抽到卡片C的概率.
22.[含评分细则](2023湖南张家界中考)(12分)阅读下面材料:
将边长分别为a,a+,a+2,a+3的正方形面积分别记为S1,S2,S3,S4,则S2-S1=(a+)2-a2=[(a+)+a]·[(a+)-a]=(2a+)·=b+2a.例如:当a=1,b=3时,S2-S1=3+2.
根据以上材料,解答下列问题:
(1)当a=1,b=3时,S3-S2= ,S4-S3= ;
(2)当a=1,b=3时,把边长为a+n的正方形的面积记作,其中n是正整数,从(1)中的计算结果,你能猜出-Sn等于多少吗 并证明你的猜想;
(3)当a=1,b=3时,令t1=S2-S1,t2=S3-S2,t3=S4-S3,……,tn=-Sn,且T=t1+t2+t3+…+t50,求T的值.
23.[含评分细则](2023吉林长春中考)(12分)【感知】如图1,点A、B、P均在☉O上,∠AOB=90°,则锐角∠APB的大小为 度.
【探究】小明遇到这样一个问题:如图2,☉O是等边三角形ABC的外接圆,点P在上(点P不与点A、C重合),连结PA、PB、PC.求证:PB=PA+PC.小明发现,延长PA至点E,使AE=PC,连结BE,通过证明△PBC≌△EBA,可推得△PBE是等边三角形,进而得证.下面是小明的部分证明过程:
证明:延长PA至点E,使AE=PC,连结BE.
∵四边形ABCP是☉O的内接四边形,
∴∠BAP+∠BCP=180°,
∵∠BAP+∠BAE=180°,∴∠BCP=∠BAE,
∵△ABC是等边三角形,∴BA=BC,
∴△PBC≌△EBA.
请你补全余下的证明过程.
【应用】如图3,☉O是△ABC的外接圆,∠ABC=90°,AB=BC,点P在☉O上,且点P与点B在AC的两侧,连结PA、PB、PC,若PB=2PA,则的值为 .
24.[含评分细则](2023吉林长春中考)(14分)在平面直角坐标系中,点O为坐标原点,抛物线y=-x2+bx+2(b是常数)经过点(2,2),点A的坐标为(m,0),点B在该抛物线上,横坐标为1-m,其中m<0.
(1)求该抛物线对应的函数表达式及顶点坐标;
(2)当点B在x轴上时,求点A的坐标;
(3)该抛物线与x轴的左交点为P,当抛物线在点P和点B之间的部分(包括P,B两点)的最高点与最低点的纵坐标之差为2-m时,求m的值;
(4)当点B在x轴上方时,过点B作BC⊥y轴于点C,连结AC、BO.若四边形AOBC的边和抛物线有两个交点(不包括四边形AOBC的顶点),设这两个交点分别为点E、点F,线段BO的中点为D.当以点C、E、O、D(或点C、F、O、D)为顶点的四边形的面积是四边形AOBC面积的一半时,直接写出所有满足条件的m的值.
答案全解全析
1.A 2 000名学生一周的课外阅读时间是总体,此调查为抽样调查,样本容量是200.
2.D 对于二次根式的乘法运算,一般地,有·=.该运算法则成立的条件是a≥0,b≥0.
3.C ∵∠ACB=60°,∴∠AOB=2∠ACB=120°,∵∠AOB=4∠BOC,∴∠BOC=30°,∴∠BAC=∠BOC=15°.
4.C 由一次函数y=kx+b的图象可得k>0,b>0,∴二次函数y=kx2+bx+2的图象开口向上,对称轴为直线x=-<0.故选C.
5.D 设AB=BC=x,扇形圆心角度数为n°,∴=x,解得n=,∴圆心角的度数为.
6.A ∵(k-3) x=k-1,∴x2-(k-3)x=k-1,∴x2-(k-3)x-k+1=0,∴Δ=[-(k-3)]2-4×1×(-k+1)=(k-1)2+4>0,∴关于x的方程(k-3) x=k-1有两个不相等的实数根.
7.C 设“立春”用A表示,“立夏”用B表示,“秋分”用C表示,“大寒”用D表示,画树状图如下,
由上可得一共有12种等可能的结果,其中小乐抽到的两张邮票恰好是“立春”和“立夏”的有2种,∴小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是=.
8.B 本题将位似与反比例函数融为一体考查,体现了数学学科的综合性.∵以原点O为位似中心,将△OAB缩小为原来的得到△OA1B1,A(2,4),B(4,1),∴A1(-1,-2),B1或A1(1,2),B1,∴A1B1的中点坐标为或,代入y=得k=-×=或k=×=.
9.D ∵抛物线开口向下,与y轴交于正半轴,对称轴在y轴右侧,∴a<0,b>0,c>0,∴<0,故①错误;∵抛物线y=ax2+bx+c经过点(-2,0),(3,0),∴对称轴为直线x=,即-=,∴a=-b,把(-2,0)代入解析式得4a-2b+c=0,∵a=-b,∴-4b-2b+c=0,∴c=6b,故②错误;∵抛物线开口向下,∴越靠近对称轴的点的纵坐标越大,∴y2
∵圆心为I,P是半圆上一动点,点D在☉I上,点Q为PD的中点,∴IQ⊥PD,故②正确;
如图,点G、Q、I、F是点Q运动中所处的位置,则GF是等腰直角三角形ABD的中位线,∴GF=AB=2,设ID交GF于点R,易知四边形GDFI为正方形,IQ⊥PD,连结QR,则QR=ID=IR=RD=RG=RF=GF=1,则点Q的运动轨迹为以R为圆心,1为半径的半圆,则点Q运动的路径长=×2π×1=π,故③正确;
由③知当点Q运动到点G的位置时,BQ的长最大,最大值为=<3.2,∴线段BQ的长不可以是3.2,故④不正确.
综上所述,正确的说法为②③,共2个.
11.x>3
解析 本题易忽略二次根式在分母的位置而致错,由题意得x-3>0,解得x>3.
12.6
解析 ∵方程x2-3x-4=0的根为x1,x2,∴x1+x2=3,x1·x2=-4,∴(x1+2)·(x2+2)=x1·x2+2x1+2x2+4=x1·x2+2(x1+x2)+4=-4+2×3+4=6.
13.>
解析 ∵二次函数y=ax2+bx+c(a>0)的图象开口向上,对称轴为直线x=1,∴越靠近对称轴的点的纵坐标y越小,∵1-(-1)=2,2-1=1,∴点(-1,y1)离对称轴的距离比点(2,y2)要远,∴y1>y2.
14.6
解析 由题意可得BC∥PQ,∴△ABD∽△AQP,∴=,即=,∴QP=6 m,∴树高PQ=6 m.
15.1.3
解析 设该门洞的半径为r m,圆心为O,连结CD、OC、OD,过O作EF⊥CD于F,交☉O于点E,则DF=CD= m,EF=r+OF=2.5 m,在Rt△OFD中,OF=,所以+r=2.5,解得r=1.3.故该门洞的半径为1.3 m.
16.(5π+32.4)
解析 竖截面的总长=AB++CD++EF=1.7+×2+29+6.7-5=(5π+32.4)m.
17.2
解析 如图,观察可知一块伞形图案的面积=正方形ABCD的面积=×2×2=2.
18.4
解析 如图,连结OC,∵EC是☉O的切线,∴∠OCE=90°,∵OD⊥BC,∴∠EDC=90°,∴∠OCD+∠ECD=∠E+∠ECD=90°,
∴∠OCD=∠E,∵OB=OC,∴∠OCD=∠B,∴∠E=∠B.∵OD⊥BC,OB=OC,
∴BD=CD=BC=4,∴DE==8,∴BC=DE,∵AB为☉O的直径,∴∠ACB=90°,∴∠ACB=∠CDE,又∵∠B=∠E,∴△ACB≌△CDE,∴AC=CD=4,∴AD==4.
19.解析 设每块澄泥砚的售价应上涨x元,则每块的销售利润为(48+x-30)元,平均每月可售出(500-10x)块,根据题意得(48+x-30)(500-10x)=11 200,整理得x2-32x+220=0,5分
解得x1=10,x2=22(不符合题意,舍去).
答:每块澄泥砚的售价应上涨10元.8分
20.解析 测角仪显示的度数为50°,∴α=90°-50°=40°,由题图①可知AB⊥BD,ED⊥BD,CE⊥AE,∴∠ABD=∠EDB=∠AED=90°,∴四边形ABDE是矩形,4分
∴AE=BD=10 m,ED=AB=1.54 m,6分
在Rt△CAE中,CE=AE·tan α≈10×0.839=8.39(m),∴CD=CE+ED=8.39+1.54=9.93≈9.9(m),即古树高度CD约为9.9 m.10分
21.解析 (1)小亮从中随机抽到卡片A的概率为.3分
(2)画树状图如下,
7分
由图可知共有9种等可能的结果,其中小亮和小刚两人都抽到卡片C的结果有1种,∴两人都抽到卡片C的概率是.10分
22.解析 (1)S3-S2=(a+2)2-(a+)2=a2+4a+4b-a2-2a-b=2a+3b,当a=1,b=3时,S3-S2=9+2.2分
S4-S3=(a+3)2-(a+2)2=a2+6a+9b-a2-4a-4b=2a+5b,当a=1,b=3时,S4-S3=15+2.4分
(2)-Sn=6n-3+2.5分
证明如下:由题目和(1)知,当a=1,b=3时,
S2-S1=(1+)2-12=3+2,
S3-S2=(1+2)2-(1+)2=9+2,
S4-S3=(1+3)2-(1+2)2=15+2,
……
∴Sn+1-Sn=(1+n)2-[1+(n-1)]2=6n-3+2.8分
(3)当a=1,b=3时,T=t1+t2+t3+…+t50=S2-S1+S3-S2+S4-S3+…+S51-S50=S51-S1=(1+50)2-12=7 500+100.12分
23.解析 【感知】∵∠AOB=90°,
∴∠APB=∠AOB=45°.3分
【探究】证明:延长PA至点E,使AE=PC,连结BE.
∵四边形ABCP是☉O的内接四边形,
∴∠BAP+∠BCP=180°,
∵∠BAP+∠BAE=180°,∴∠BCP=∠BAE,
∵△ABC是等边三角形,∴BA=BC,
∴△PBC≌△EBA.
∴PB=EB,∵△ABC是等边三角形,∴∠ACB=60°,∴∠APB=60°,∴△PBE为等边三角形,∴PB=PE=AP+AE=PA+PC.8分
【应用】如图,延长PA至点G,使AG=PC,连结BG.∵四边形ABCP是☉O的内接四边形,∴∠BAP+∠BCP=180°,∵∠BAP+∠BAG=180°,∴∠BCP=∠BAG,∵BA=BC,
∴△PBC≌△GBA,∴PB=GB,∠PBC=∠GBA,∵∠ABC=90°,∴∠PBG=∠GBA+∠ABP=∠PBC+∠ABP=∠ABC=90°,∴PG=BP=4PA,
∵PG=PA+AG=PA+PC,∴PC=PG-PA=4PA-PA=3PA,∴==.12分
24.解析 (1)将点(2,2)代入抛物线y=-x2+bx+2中得2=-4+2b+2,解得b=2,∴抛物线的解析式为y=-x2+2x+2=-(x-1)2+3,∴顶点坐标为(1,3).2分
(2)当y=0时,-x2+2x+2=0,解得x1=1-,x2=1+,∵点B的横坐标为1-m,其中m<0,∴1-m>1,∴1-m=1+,解得m=-,∵点A的坐标为(m,0),∴A(-,0).4分
(3)由(2)知,P(1-,0),∵m<0,∴1-m>1,∴点B一定在对称轴右侧,∴B(1-m,-m2+3),5分
分情况求解如下:
①如图a所示,当1<1-m<1+,即-
综上所述,m=-1或m=-2.
(4)如图1所示,连结CD,∵B在x轴的上方,∴1-<1-m<1+且m<0,∴-
①当E是AC的中点,即E时,如图2,连结OE,则S△AOE=S△COE,此时S四边形AOBC=S四边形CEOD,将E代入y=-x2+2x+2,得=-+2×+2,解得m=--2(舍去)或m=-2+;10分
②同理当F为AO的中点,即F时,如图3所示,连结CF,则S△ACF=S△CFO,此时S四边形AOBC=S四边形CFOD,∴=1-,解得m=2-2;12分
③如图4所示,连结DF,∵以点C、F、O、D为顶点的四边形的面积是四边形AOBC面积的一半,∴S△COD+S△CFD=S四边形AOBC=(S△AOC+S△BCO),∵S△BCD=S△COD,∴S△CFD=S△AOC,∵D为OB的中点,∴CF=OA,∴F(-m,-m2+3),∵B,F关于直线x=1对称,∴=1,解得m=-.14分
综上所述,m=-2+或m=2-2或m=-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
