2024华东师大版数学九年级下学期课时练--期末素养综合测试(一)(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--期末素养综合测试(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 565.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 20:43:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023浙江嘉兴中考)在下面的调查中,最适合用全面调查的是( )
A.了解一批节能灯管的使用寿命
B.了解某校803班学生的视力情况
C.了解某省初中生每周上网时长情况
D.了解京杭大运河中鱼的种类
2.(2023吉林松原长岭模拟)如图,AB是☉O的直径,∠D=32°,则∠AOC等于( )
A.158° B.58° C.64° D.116°
3.【新素材】(2023河北秦皇岛昌黎期中)某班在开展“节约每一滴水”的活动中,从全班40名同学中选出10名同学汇报了各自家庭一个月的节水情况,发现节水0.5 m3的有2人,节水1 m3的有3人,节水1.5 m3的有2人,节水2 m3的有3人,用所学的统计知识估计全班同学的家庭一个月节约用水的总量是( )
A.20 m3 B.52 m3 C.60 m3 D.100 m3
4.(2023河南驻马店模拟)若抛物线y=x2+2x-3不动,将平面直角坐标系先沿水平方向向左平移2个单位长度,再沿铅垂方向向下平移3个单位长度,则原抛物线的解析式应变为( )
A.y=(x-2)2+3 B.y=(x-1)2-1
C.y=(x+3)2-7 D.y=x2+4
5.【易错题】(2023福建厦门思明月考)二次函数y=cx2-4x+2c的图象的最高点在x轴上,则c的值是 ( )
A. B.- C.±2 D.±
6.(2022江苏南京溧水期末)如图,四边形ABCD内接于☉O,∠BAD=90°,AB=AD,∠ADC=105°.若点E在上,且=2,连结AE,则∠BAE的度数是( )
A.15° B.20°
C.25° D.30°
7.【新考法】(2023广东珠海香洲凤凰中学模拟)设圆锥的底面圆半径为r,圆锥的母线长为l,满足r+l=6,这样的圆锥的侧面积( )
A.有最大值 B.有最小值
C.有最大值9π D.有最小值9π
8.【新素材】(2023河北石家庄四十二中模拟)有一款带毛刷的圆形扫地机器人,它的俯视图如图所示,☉O的直径为40 cm,毛刷的一端为固定点P,另一端为点C,CP=10 cm,毛刷绕着点P旋转形成的圆弧交☉O于点A,B,且A,P,B三点在同一直线上,则图中阴影部分的周长为( )
A.20π cm B.20π cm
C.(20-10)π cm D.(10+10)π cm
9.(2023河北衡水模拟)某水利工程公司开挖的沟渠,蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).
某学习小组探究之后得出如下结论,其中正确的为( )
A.AB=24 m
B.沟底所在抛物线的解析式为y=x2-5
C.沟渠最深处到水面CD的距离为3.2 m
D.若沟渠中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的
10.(2023湖北鄂州中考)已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且过点(-1,0),顶点在第一象限,其部分图象如图所示.给出以下结论:①ab<0;②4a+2b+c>0;③3a+c>0;④若A(x1,y1),B(x2,y2)(其中x12,则y1>y2.其中正确的是 ( )
A.①②③ B.①③④ C.②③④ D.①②④
二、填空题(每小题3分,共24分)
11.(2023四川攀枝花仁和模拟)要想了解九年级1 500名学生的心理健康评估报告,从中抽取了300名学生的心理健康评估报告进行统计分析,以下说法:①每名学生的心理健康评估报告是个体;②1 500名学生是总体;③被抽取的300名学生是总体的一个样本;④300是样本容量.其中正确的是 .
12.若☉O的半径为4 cm,点P到圆心O的距离为5 cm,则点P与☉O的位置关系是 .
13.(2023山东济宁汶上模拟)一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺进行了如图所示的测量,测得AB=12,BC=5,则圆形镜面的半径为 .
14.(2023云南昆明官渡模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx(a>0)和直线y=kx(k>0)交于点O和点A,则不等式ax2+bx15.(2022山东青岛市北期末)某公司2018年~2020年的产品价格如下表所示:
年份 2018 2019 2020
价格(元/500克) 1.46 1.92 2.53
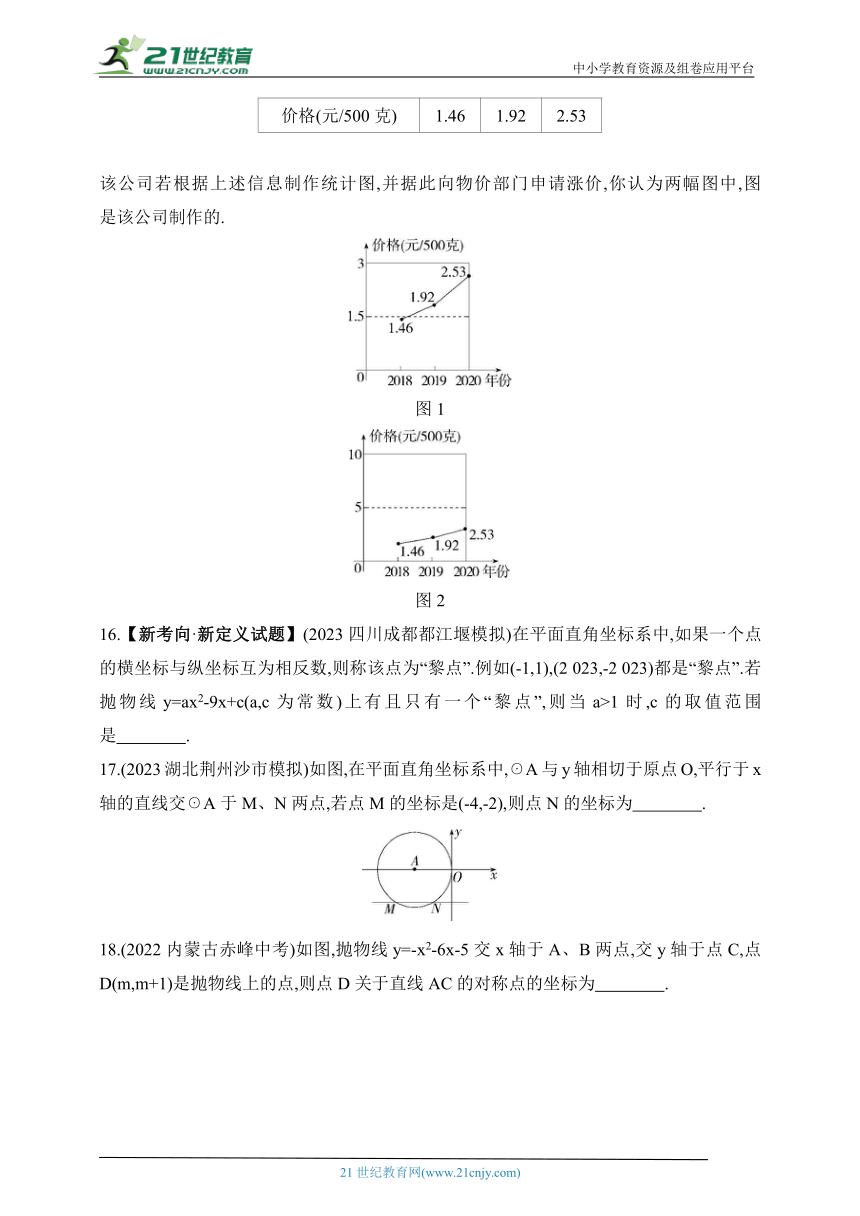
该公司若根据上述信息制作统计图,并据此向物价部门申请涨价,你认为两幅图中,图 是该公司制作的.
图1
图2
16.【新考向·新定义试题】(2023四川成都都江堰模拟)在平面直角坐标系中,如果一个点的横坐标与纵坐标互为相反数,则称该点为“黎点”.例如(-1,1),(2 023,-2 023)都是“黎点”.若抛物线y=ax2-9x+c(a,c为常数)上有且只有一个“黎点”,则当a>1时,c的取值范围是 .
17.(2023湖北荆州沙市模拟)如图,在平面直角坐标系中,☉A与y轴相切于原点O,平行于x轴的直线交☉A于M、N两点,若点M的坐标是(-4,-2),则点N的坐标为 .
18.(2022内蒙古赤峰中考)如图,抛物线y=-x2-6x-5交x轴于A、B两点,交y轴于点C,点D(m,m+1)是抛物线上的点,则点D关于直线AC的对称点的坐标为 .
三、解答题(共66分)
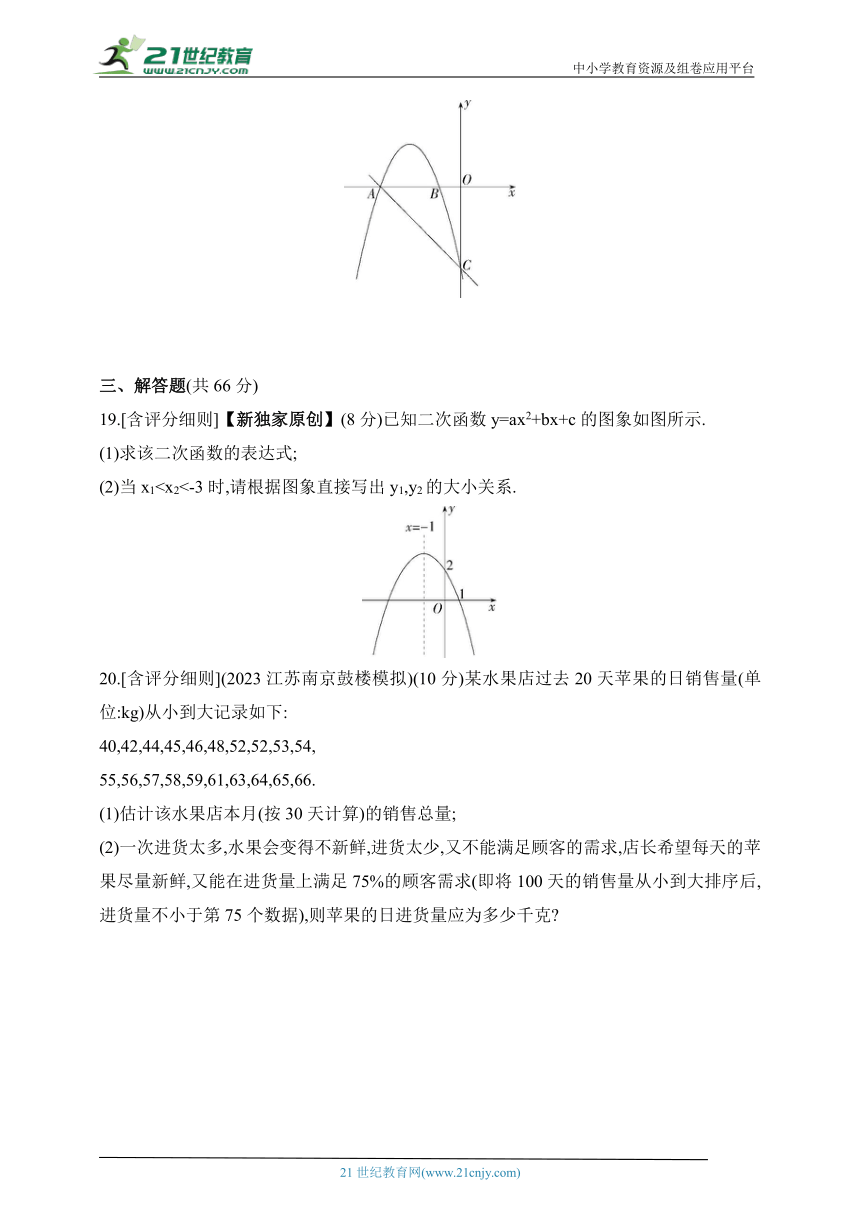
19.[含评分细则]【新独家原创】(8分)已知二次函数y=ax2+bx+c的图象如图所示.
(1)求该二次函数的表达式;
(2)当x120.[含评分细则](2023江苏南京鼓楼模拟)(10分)某水果店过去20天苹果的日销售量(单位:kg)从小到大记录如下:
40,42,44,45,46,48,52,52,53,54,
55,56,57,58,59,61,63,64,65,66.
(1)估计该水果店本月(按30天计算)的销售总量;
(2)一次进货太多,水果会变得不新鲜,进货太少,又不能满足顾客的需求,店长希望每天的苹果尽量新鲜,又能在进货量上满足75%的顾客需求(即将100天的销售量从小到大排序后,进货量不小于第75个数据),则苹果的日进货量应为多少千克
21.[含评分细则]【生命安全与健康】(2023浙江丽水中考)(10分)为全面提升中小学生体质健康水平,我市开展了儿童青少年“正脊行动”.人民医院专家组随机抽取某校各年级部分学生进行了脊柱健康状况筛查.根据筛查情况,李老师绘制了两幅不完整的统计图表.
抽取的学生脊柱健康情况统计表
类别 检查结果 人数
A 正常 170
B 轻度侧弯
C 中度侧弯 7
D 重度侧弯
请根据图表信息解答下列问题:
(1)求所抽取的学生总人数并完成表格;
(2)该校共有学生1 600人,请估算脊柱侧弯程度为中度和重度的总人数;
(3)为保护学生脊柱健康,请结合上述统计数据,提出一条合理的建议.
22.[含评分细则](2022江苏宿迁中考)(12分)如图,在△ABC中,∠ABC=45°,AB=AC,以AB为直径的☉O与边BC交于点D.
(1)判断直线AC与☉O的位置关系,并说明理由;
(2)若AB=4,求图中阴影部分的面积.
23.[含评分细则]【中华优秀传统文化】(2023河南漯河召陵模拟)(12分)木质风车作为一种农具在我国有着悠久的历史,其基本构造是顶部有个梯形的入料仓,下面有一个漏斗是出大米的,右面是圆形的风箱部分,侧面有一个小漏斗是出细米、瘪粒的,尾部是出谷壳的,其实物图如图1所示.爱动脑筋的东东对风车进行了探究和测量,并画出了风箱部分的简易示意图(图2),AE为☉O的直径,B是☉O上的一点,过点B作BC⊥AE交☉O于点C,交AE于点D(点D在点O下方),地面上的点F在AD的延长线上,连结CF,测得AD=BC=80 cm,∠BCF=∠BAC.
(1)求证:CF是☉O的切线;
(2)求风车中心O到地面F的距离.
24.[含评分细则](2021内蒙古赤峰中考)(14分)如图,抛物线y=-x2+bx+c与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C,对称轴l与x轴交于点F,直线m∥AC,点E是直线AC上方抛物线上一动点,过点E作EH⊥m,垂足为H,交AC于点G,连结AE、EC、CH、AH.
(1)抛物线的解析式为 ;
(2)当四边形AHCE的面积最大时,求点E的坐标;
(3)在(2)的条件下,连结EF,点P是x轴上一动点,在抛物线上是否存在点Q,使得以F、E、P、Q为顶点,以EF为一边的四边形是平行四边形 若存在,请直接写出点Q的坐标;若不存在,请说明理由.
答案全解全析
1.B 选项A中的事件具有破坏性,选项C、D中的事件涉及面广,故均应采用抽样调查的方式.故选B.
2.D ∵∠D=32°,∴∠BOC=2∠D=64°,∴∠AOC=180°-64°=116°.
3.B 选出的10名同学节水的平均数==1.3(m3),则全班同学的家庭一个月节约用水的总量约为1.3×40=52(m3).
4.B 将平面直角坐标系xOy先沿水平方向向左平移2个单位长度,再沿铅垂方向向下平移3个单位长度,相当于把抛物线向右平移2个单位长度,再向上平移3个单位长度,∵y=x2+2x-3=(x+1)2-4,∴原抛物线的解析式应变为y=(x+1-2)2-4+3=(x-1)2-1.
5.B 易错点:易忽视“图象的最高点”这一限制条件.
二次函数y=cx2-4x+2c的图象的顶点的纵坐标为.∵抛物线的顶点在x轴上,
∴=0,解得c=±.∵抛物线有最高点,∴c=-.故选B.
6.B 如图,连结BD,DE,∵∠BAD=90°,AB=AD,∴∠ABD=∠ADB=45°,∵∠ADC=105°,∴∠BDC=
105°-45°=60°,∵=2,∴∠BDE=∠CDE=∠BDC=20°,∴∠BAE=∠BDE=20°.
7.C 本题将圆锥侧面积和二次函数的最值融为一体考查,设计巧妙.由题意知S=πrl=πr(6-r)=-π(r-3)2+9π,∵-π<0,∴当r=3时,S有最大值9π.
8.D 如图,连结AB,OA,OB,OP,∵A,P,B三点在同一直线上,∴AB经过点P,由题意得AB为所在圆的直径,PB=PA=CP=10 cm,OA=OB=20 cm,∴OP⊥AB,在Rt△OAP中,sin∠AOP===,∴∠AOP=45°,∵OA=OB,OP⊥AB,∴∠BOP=∠AOP=45°,∴∠AOB=90°,∴l==10π(cm),l==10π(cm),∴阴影部分的周长为10π+10π=(10+10)π cm.
9.C AB=15-(-15)=30(m),故A错误;设抛物线解析式为y=ax2+bx+c(a≠0),将A(-15,0),B(15,0),P(0,-5)代入抛物线解析式得解得∴解析式为y=x2-5,故B错误;当x=12时,y=×122-5=-1.8,-1.8-(-5)=3.2(m),所以沟渠最深处到水面CD的距离为3.2 m,故C正确;当沟渠中水面的宽度减少为原来的一半,即水面宽度为12 m时,将x=6代入解析式得y=×62-5=-5=-,此时最深处到水面的距离为--(-5)=0.8 m,减少为原来的,故D错误.
10.D ∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=1,∴-=1,∴b=-2a,∴b>0,∴ab<0,故①正确;∵抛物线过点(-1,0),∴由对称可得抛物线与x轴的另一交点为(3,0),由函数图象可得x=2时,y>0,∴4a+2b+c>0,故②正确;∵x=-1时,y=0,∴a-b+c=0,又∵b=-2a,∴3a+c=0,故③错误;∵对称轴是直线x=1,∴若A、B两点关于直线x=1对称,则=1,∴当x1+x2>2时,点A(x1,y1)到对称轴的距离小于点B(x2,y2)到对称轴的距离,∵二次函数图象开口向下,∴y1>y2,故④正确.综上所述,正确的是①②④.
11.①④
解析 每名学生的心理健康评估报告是个体,1 500名学生的心理健康评估报告是总体,被抽取的300名学生的心理健康评估报告是总体的一个样本,300是样本容量,故正确的是①④.
12.点P在☉O外
解析 ∵☉O的半径r=4 cm,点P到圆心O的距离d=5 cm,∴r13.
解析 如图,连结AC,∵∠ABC=90°,且∠ABC是圆周角,∴AC是圆形镜面的直径,由勾股定理得AC===13,∴圆形镜面的半径为.
14.0解析 根据题图可知,当015.2
解析 因为该公司要根据统计图向物价部门申请涨价,题图2的折线图较平缓,所以题图2是该公司制作的.
16.0解析 ∵抛物线y=ax2-9x+c上有且只有一个“黎点”,∴方程ax2-9x+c=-x(a≠0)有且只有一个解,方程整理可得ax2-8x+c=0,即有Δ=64-4ac=0,解得ac=16,∴a=,∵a>1,∴017.(-1,-2)
解析 如图,过点A作AB⊥MN于点B,连结AN,则BM=BN,设☉A的半径为r,则AN=r,AB=2,BM=BN=4-r,在Rt△ABN中,根据勾股定理得22+(4-r)2=r2,解得r=2.5,∴BN=4-2.5=1.5,则N到y轴的距离为AO-BN=2.5-1.5=1,∵点N在第三象限,∴点N的坐标为(-1,-2).
18.(-5,-4)或(0,1)
解析 把点D(m,m+1)代入抛物线y=-x2-6x-5,得m+1=-m2-6m-5,解得m1=-1,m2=-6,
∴D的坐标为(-1,0)或(-6,-5).
当y=0时,-x2-6x-5=0,
∴x=-1或-5,∴A(-5,0),B(-1,0),
当x=0时,y=-5,∴OC=OA=5,
∴△AOC是等腰直角三角形,
∴∠OAC=45°.
①如图,D的坐标为(-1,0)时,点D与点B重合,
设点D关于直线AC的对称点为D',连结AD',
易知AC是BD'的垂直平分线,
∴AB=AD'=-1-(-5)=4,且∠OAC=∠CAD'=45°,
∴∠OAD'=90°,
∴D'(-5,-4);
②如图,当点D的坐标为(-6,-5)时,设点D关于直线AC的对称点为D',DD'与AC交于点E,
∵点D(m,m+1),
∴点D在直线y=x+1上,此时直线y=x+1过点B,
∵BD⊥AC,∴D'在直线y=x+1上,
∵A(-5,0),C(0,-5),
∴直线AC的解析式为y=-x-5,
令-x-5=x+1,解得x=-3,
∴E(-3,-2),
∵点D与D'关于直线AC对称,
∴E是DD'的中点,∴D'(0,1).
综上,点D关于直线AC的对称点的坐标为(-5,-4)或(0,1).
19.解析 (1)由图象可知抛物线与y轴的交点坐标为(0,2),与x轴的一个交点坐标为(1,0),对称轴为直线x=-1,根据抛物线的对称性易知图象与x轴的另一交点坐标为(-3,0).3分
设二次函数表达式为y=a(x+3)(x-1)(a≠0),化简整理得y=ax2+2ax-3a,将(0,2)代入可得-3a=2,解得a=-,所以二次函数的表达式为y=-x2-x+2.5分
(2)由图象可知,当x120.解析 (1)×(40+42+44+45+46+48+52+52+53+54+55+56+57+58+59+61+63+64+65+66)×30=1 620(kg).
答:估计该水果店本月(按30天计算)的销售总量为1 620 kg.5分
(2)∵20×75%=15,样本中的数从小到大排列后,排在第15个的数是59,∴苹果的日进货量应为59千克. 10分
21.解析 (1)抽取的学生总人数是170÷85%=200,
2分
200×10%=20(人),200-170-20-7=3(人),填表如下:
类别 检查结果 人数
A 正常 170
B 轻度侧弯 20
C 中度侧弯 7
D 重度侧弯 3
4分
(2)1 600×(1-10%-85%)=1 600×5%=80(人),故估计脊柱侧弯程度为中度和重度的总人数是80.8分
(3)答案不唯一,如:该校学生脊柱侧弯人数占15%,说明该校学生脊柱侧弯情况较为严重,建议学校要每天组织学生做护脊操等.10分
22.解析 (1)直线AC与☉O相切.1分
理由如下:
∵∠ABC=45°,AB=AC,
∴∠C=∠ABC=45°,2分
∴∠BAC=180°-2×45°=90°,
∴BA⊥AC.4分
∵AB是☉O的直径,
∴直线AC与☉O相切.6分
(2)如图,连结OD,
∵∠ABD=45°,∴∠AOD=2∠ABD=90°.7分
∴∠BOD=90°.
∵AB=4,AB=AC,∴OA=OD=OB=2,AC=4,8分
∴S阴影=S△ABC-S△BOD-S扇形AOD=×4×4-×2×2-=8-2-π=6-π.12分
23.解析 (1)证明:如图,连结CO并延长交☉O于点G,连结BG,∵∠BAC=∠BCF,∠BGC=∠BAC,∴∠BCF=∠BGC,2分
∵CG是☉O的直径,∴∠GBC=90°,∴∠BGC+∠GCB=90°,∴∠BCF+∠GCB=90°,即∠GCF=90°,∴OC⊥CF,4分
∵OC为☉O的半径,∴CF为☉O的切线.5分
(2)∵AE为☉O的直径,AE⊥BC,BC=80 cm,∴BD=DC=BC=40 cm,6分
设☉O的半径为r cm,∴OD=(80-r)cm,
在Rt△ODC中,OD2+DC2=OC2,
∴(80-r)2+402=r2,
∴r=50,∴OC=50 cm,OD=30 cm,8分
∵∠DOC=∠COF,∠ODC=∠OCF=90°,
∴△ODC∽△OCF,10分
∴=,∴=,∴OF= cm,
∴风车中心O到地面F的距离为 cm.12分
24.解析 (1)y=-x2-2x+3.3分
(2)如图,连结OE.设E(n,-n2-2n+3),
∵点E在直线AC上方,∴n<0,-n2-2n+3>0,
∵A(-3,0),C(0,3),∴OA=OC=3,AC=3.
∵AC∥直线m,∴△ACH的面积是定值.4分
∵S四边形AECH=S△AEC+S△ACH,
∴当△AEC的面积最大时,四边形AECH的面积最大.5分
S△AEC=S△AEO+S△ECO-S△AOC=×3×(-n2-2n+3)+×3×(-n)-×3×3=-+.6分
∵-<0,∴n=-时,△AEC的面积最大,7分
∴E.8分
(3)存在.点Q的坐标为或或.14分
[详解]如图,由点P在x轴上,点Q在抛物线上,EF是平行四边形的边可知满足条件的点Q的纵坐标为±,
对于抛物线y=-x2-2x+3,当y=时,-x2-2x+3=,解得x=-(舍去)或x=-,∴Q1.
当y=-时,-x2-2x+3=-,解得x=,
∴Q2,Q3.
综上所述,满足条件的点Q的坐标为或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023浙江嘉兴中考)在下面的调查中,最适合用全面调查的是( )
A.了解一批节能灯管的使用寿命
B.了解某校803班学生的视力情况
C.了解某省初中生每周上网时长情况
D.了解京杭大运河中鱼的种类
2.(2023吉林松原长岭模拟)如图,AB是☉O的直径,∠D=32°,则∠AOC等于( )
A.158° B.58° C.64° D.116°
3.【新素材】(2023河北秦皇岛昌黎期中)某班在开展“节约每一滴水”的活动中,从全班40名同学中选出10名同学汇报了各自家庭一个月的节水情况,发现节水0.5 m3的有2人,节水1 m3的有3人,节水1.5 m3的有2人,节水2 m3的有3人,用所学的统计知识估计全班同学的家庭一个月节约用水的总量是( )
A.20 m3 B.52 m3 C.60 m3 D.100 m3
4.(2023河南驻马店模拟)若抛物线y=x2+2x-3不动,将平面直角坐标系先沿水平方向向左平移2个单位长度,再沿铅垂方向向下平移3个单位长度,则原抛物线的解析式应变为( )
A.y=(x-2)2+3 B.y=(x-1)2-1
C.y=(x+3)2-7 D.y=x2+4
5.【易错题】(2023福建厦门思明月考)二次函数y=cx2-4x+2c的图象的最高点在x轴上,则c的值是 ( )
A. B.- C.±2 D.±
6.(2022江苏南京溧水期末)如图,四边形ABCD内接于☉O,∠BAD=90°,AB=AD,∠ADC=105°.若点E在上,且=2,连结AE,则∠BAE的度数是( )
A.15° B.20°
C.25° D.30°
7.【新考法】(2023广东珠海香洲凤凰中学模拟)设圆锥的底面圆半径为r,圆锥的母线长为l,满足r+l=6,这样的圆锥的侧面积( )
A.有最大值 B.有最小值
C.有最大值9π D.有最小值9π
8.【新素材】(2023河北石家庄四十二中模拟)有一款带毛刷的圆形扫地机器人,它的俯视图如图所示,☉O的直径为40 cm,毛刷的一端为固定点P,另一端为点C,CP=10 cm,毛刷绕着点P旋转形成的圆弧交☉O于点A,B,且A,P,B三点在同一直线上,则图中阴影部分的周长为( )
A.20π cm B.20π cm
C.(20-10)π cm D.(10+10)π cm
9.(2023河北衡水模拟)某水利工程公司开挖的沟渠,蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).
某学习小组探究之后得出如下结论,其中正确的为( )
A.AB=24 m
B.沟底所在抛物线的解析式为y=x2-5
C.沟渠最深处到水面CD的距离为3.2 m
D.若沟渠中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的
10.(2023湖北鄂州中考)已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且过点(-1,0),顶点在第一象限,其部分图象如图所示.给出以下结论:①ab<0;②4a+2b+c>0;③3a+c>0;④若A(x1,y1),B(x2,y2)(其中x1
A.①②③ B.①③④ C.②③④ D.①②④
二、填空题(每小题3分,共24分)
11.(2023四川攀枝花仁和模拟)要想了解九年级1 500名学生的心理健康评估报告,从中抽取了300名学生的心理健康评估报告进行统计分析,以下说法:①每名学生的心理健康评估报告是个体;②1 500名学生是总体;③被抽取的300名学生是总体的一个样本;④300是样本容量.其中正确的是 .
12.若☉O的半径为4 cm,点P到圆心O的距离为5 cm,则点P与☉O的位置关系是 .
13.(2023山东济宁汶上模拟)一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺进行了如图所示的测量,测得AB=12,BC=5,则圆形镜面的半径为 .
14.(2023云南昆明官渡模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx(a>0)和直线y=kx(k>0)交于点O和点A,则不等式ax2+bx
年份 2018 2019 2020
价格(元/500克) 1.46 1.92 2.53
该公司若根据上述信息制作统计图,并据此向物价部门申请涨价,你认为两幅图中,图 是该公司制作的.
图1
图2
16.【新考向·新定义试题】(2023四川成都都江堰模拟)在平面直角坐标系中,如果一个点的横坐标与纵坐标互为相反数,则称该点为“黎点”.例如(-1,1),(2 023,-2 023)都是“黎点”.若抛物线y=ax2-9x+c(a,c为常数)上有且只有一个“黎点”,则当a>1时,c的取值范围是 .
17.(2023湖北荆州沙市模拟)如图,在平面直角坐标系中,☉A与y轴相切于原点O,平行于x轴的直线交☉A于M、N两点,若点M的坐标是(-4,-2),则点N的坐标为 .
18.(2022内蒙古赤峰中考)如图,抛物线y=-x2-6x-5交x轴于A、B两点,交y轴于点C,点D(m,m+1)是抛物线上的点,则点D关于直线AC的对称点的坐标为 .
三、解答题(共66分)
19.[含评分细则]【新独家原创】(8分)已知二次函数y=ax2+bx+c的图象如图所示.
(1)求该二次函数的表达式;
(2)当x1
40,42,44,45,46,48,52,52,53,54,
55,56,57,58,59,61,63,64,65,66.
(1)估计该水果店本月(按30天计算)的销售总量;
(2)一次进货太多,水果会变得不新鲜,进货太少,又不能满足顾客的需求,店长希望每天的苹果尽量新鲜,又能在进货量上满足75%的顾客需求(即将100天的销售量从小到大排序后,进货量不小于第75个数据),则苹果的日进货量应为多少千克
21.[含评分细则]【生命安全与健康】(2023浙江丽水中考)(10分)为全面提升中小学生体质健康水平,我市开展了儿童青少年“正脊行动”.人民医院专家组随机抽取某校各年级部分学生进行了脊柱健康状况筛查.根据筛查情况,李老师绘制了两幅不完整的统计图表.
抽取的学生脊柱健康情况统计表
类别 检查结果 人数
A 正常 170
B 轻度侧弯
C 中度侧弯 7
D 重度侧弯
请根据图表信息解答下列问题:
(1)求所抽取的学生总人数并完成表格;
(2)该校共有学生1 600人,请估算脊柱侧弯程度为中度和重度的总人数;
(3)为保护学生脊柱健康,请结合上述统计数据,提出一条合理的建议.
22.[含评分细则](2022江苏宿迁中考)(12分)如图,在△ABC中,∠ABC=45°,AB=AC,以AB为直径的☉O与边BC交于点D.
(1)判断直线AC与☉O的位置关系,并说明理由;
(2)若AB=4,求图中阴影部分的面积.
23.[含评分细则]【中华优秀传统文化】(2023河南漯河召陵模拟)(12分)木质风车作为一种农具在我国有着悠久的历史,其基本构造是顶部有个梯形的入料仓,下面有一个漏斗是出大米的,右面是圆形的风箱部分,侧面有一个小漏斗是出细米、瘪粒的,尾部是出谷壳的,其实物图如图1所示.爱动脑筋的东东对风车进行了探究和测量,并画出了风箱部分的简易示意图(图2),AE为☉O的直径,B是☉O上的一点,过点B作BC⊥AE交☉O于点C,交AE于点D(点D在点O下方),地面上的点F在AD的延长线上,连结CF,测得AD=BC=80 cm,∠BCF=∠BAC.
(1)求证:CF是☉O的切线;
(2)求风车中心O到地面F的距离.
24.[含评分细则](2021内蒙古赤峰中考)(14分)如图,抛物线y=-x2+bx+c与x轴交于A(-3,0)、B(1,0)两点,与y轴交于点C,对称轴l与x轴交于点F,直线m∥AC,点E是直线AC上方抛物线上一动点,过点E作EH⊥m,垂足为H,交AC于点G,连结AE、EC、CH、AH.
(1)抛物线的解析式为 ;
(2)当四边形AHCE的面积最大时,求点E的坐标;
(3)在(2)的条件下,连结EF,点P是x轴上一动点,在抛物线上是否存在点Q,使得以F、E、P、Q为顶点,以EF为一边的四边形是平行四边形 若存在,请直接写出点Q的坐标;若不存在,请说明理由.
答案全解全析
1.B 选项A中的事件具有破坏性,选项C、D中的事件涉及面广,故均应采用抽样调查的方式.故选B.
2.D ∵∠D=32°,∴∠BOC=2∠D=64°,∴∠AOC=180°-64°=116°.
3.B 选出的10名同学节水的平均数==1.3(m3),则全班同学的家庭一个月节约用水的总量约为1.3×40=52(m3).
4.B 将平面直角坐标系xOy先沿水平方向向左平移2个单位长度,再沿铅垂方向向下平移3个单位长度,相当于把抛物线向右平移2个单位长度,再向上平移3个单位长度,∵y=x2+2x-3=(x+1)2-4,∴原抛物线的解析式应变为y=(x+1-2)2-4+3=(x-1)2-1.
5.B 易错点:易忽视“图象的最高点”这一限制条件.
二次函数y=cx2-4x+2c的图象的顶点的纵坐标为.∵抛物线的顶点在x轴上,
∴=0,解得c=±.∵抛物线有最高点,∴c=-.故选B.
6.B 如图,连结BD,DE,∵∠BAD=90°,AB=AD,∴∠ABD=∠ADB=45°,∵∠ADC=105°,∴∠BDC=
105°-45°=60°,∵=2,∴∠BDE=∠CDE=∠BDC=20°,∴∠BAE=∠BDE=20°.
7.C 本题将圆锥侧面积和二次函数的最值融为一体考查,设计巧妙.由题意知S=πrl=πr(6-r)=-π(r-3)2+9π,∵-π<0,∴当r=3时,S有最大值9π.
8.D 如图,连结AB,OA,OB,OP,∵A,P,B三点在同一直线上,∴AB经过点P,由题意得AB为所在圆的直径,PB=PA=CP=10 cm,OA=OB=20 cm,∴OP⊥AB,在Rt△OAP中,sin∠AOP===,∴∠AOP=45°,∵OA=OB,OP⊥AB,∴∠BOP=∠AOP=45°,∴∠AOB=90°,∴l==10π(cm),l==10π(cm),∴阴影部分的周长为10π+10π=(10+10)π cm.
9.C AB=15-(-15)=30(m),故A错误;设抛物线解析式为y=ax2+bx+c(a≠0),将A(-15,0),B(15,0),P(0,-5)代入抛物线解析式得解得∴解析式为y=x2-5,故B错误;当x=12时,y=×122-5=-1.8,-1.8-(-5)=3.2(m),所以沟渠最深处到水面CD的距离为3.2 m,故C正确;当沟渠中水面的宽度减少为原来的一半,即水面宽度为12 m时,将x=6代入解析式得y=×62-5=-5=-,此时最深处到水面的距离为--(-5)=0.8 m,减少为原来的,故D错误.
10.D ∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=1,∴-=1,∴b=-2a,∴b>0,∴ab<0,故①正确;∵抛物线过点(-1,0),∴由对称可得抛物线与x轴的另一交点为(3,0),由函数图象可得x=2时,y>0,∴4a+2b+c>0,故②正确;∵x=-1时,y=0,∴a-b+c=0,又∵b=-2a,∴3a+c=0,故③错误;∵对称轴是直线x=1,∴若A、B两点关于直线x=1对称,则=1,∴当x1+x2>2时,点A(x1,y1)到对称轴的距离小于点B(x2,y2)到对称轴的距离,∵二次函数图象开口向下,∴y1>y2,故④正确.综上所述,正确的是①②④.
11.①④
解析 每名学生的心理健康评估报告是个体,1 500名学生的心理健康评估报告是总体,被抽取的300名学生的心理健康评估报告是总体的一个样本,300是样本容量,故正确的是①④.
12.点P在☉O外
解析 ∵☉O的半径r=4 cm,点P到圆心O的距离d=5 cm,∴r
解析 如图,连结AC,∵∠ABC=90°,且∠ABC是圆周角,∴AC是圆形镜面的直径,由勾股定理得AC===13,∴圆形镜面的半径为.
14.0
解析 因为该公司要根据统计图向物价部门申请涨价,题图2的折线图较平缓,所以题图2是该公司制作的.
16.0
解析 如图,过点A作AB⊥MN于点B,连结AN,则BM=BN,设☉A的半径为r,则AN=r,AB=2,BM=BN=4-r,在Rt△ABN中,根据勾股定理得22+(4-r)2=r2,解得r=2.5,∴BN=4-2.5=1.5,则N到y轴的距离为AO-BN=2.5-1.5=1,∵点N在第三象限,∴点N的坐标为(-1,-2).
18.(-5,-4)或(0,1)
解析 把点D(m,m+1)代入抛物线y=-x2-6x-5,得m+1=-m2-6m-5,解得m1=-1,m2=-6,
∴D的坐标为(-1,0)或(-6,-5).
当y=0时,-x2-6x-5=0,
∴x=-1或-5,∴A(-5,0),B(-1,0),
当x=0时,y=-5,∴OC=OA=5,
∴△AOC是等腰直角三角形,
∴∠OAC=45°.
①如图,D的坐标为(-1,0)时,点D与点B重合,
设点D关于直线AC的对称点为D',连结AD',
易知AC是BD'的垂直平分线,
∴AB=AD'=-1-(-5)=4,且∠OAC=∠CAD'=45°,
∴∠OAD'=90°,
∴D'(-5,-4);
②如图,当点D的坐标为(-6,-5)时,设点D关于直线AC的对称点为D',DD'与AC交于点E,
∵点D(m,m+1),
∴点D在直线y=x+1上,此时直线y=x+1过点B,
∵BD⊥AC,∴D'在直线y=x+1上,
∵A(-5,0),C(0,-5),
∴直线AC的解析式为y=-x-5,
令-x-5=x+1,解得x=-3,
∴E(-3,-2),
∵点D与D'关于直线AC对称,
∴E是DD'的中点,∴D'(0,1).
综上,点D关于直线AC的对称点的坐标为(-5,-4)或(0,1).
19.解析 (1)由图象可知抛物线与y轴的交点坐标为(0,2),与x轴的一个交点坐标为(1,0),对称轴为直线x=-1,根据抛物线的对称性易知图象与x轴的另一交点坐标为(-3,0).3分
设二次函数表达式为y=a(x+3)(x-1)(a≠0),化简整理得y=ax2+2ax-3a,将(0,2)代入可得-3a=2,解得a=-,所以二次函数的表达式为y=-x2-x+2.5分
(2)由图象可知,当x1
答:估计该水果店本月(按30天计算)的销售总量为1 620 kg.5分
(2)∵20×75%=15,样本中的数从小到大排列后,排在第15个的数是59,∴苹果的日进货量应为59千克. 10分
21.解析 (1)抽取的学生总人数是170÷85%=200,
2分
200×10%=20(人),200-170-20-7=3(人),填表如下:
类别 检查结果 人数
A 正常 170
B 轻度侧弯 20
C 中度侧弯 7
D 重度侧弯 3
4分
(2)1 600×(1-10%-85%)=1 600×5%=80(人),故估计脊柱侧弯程度为中度和重度的总人数是80.8分
(3)答案不唯一,如:该校学生脊柱侧弯人数占15%,说明该校学生脊柱侧弯情况较为严重,建议学校要每天组织学生做护脊操等.10分
22.解析 (1)直线AC与☉O相切.1分
理由如下:
∵∠ABC=45°,AB=AC,
∴∠C=∠ABC=45°,2分
∴∠BAC=180°-2×45°=90°,
∴BA⊥AC.4分
∵AB是☉O的直径,
∴直线AC与☉O相切.6分
(2)如图,连结OD,
∵∠ABD=45°,∴∠AOD=2∠ABD=90°.7分
∴∠BOD=90°.
∵AB=4,AB=AC,∴OA=OD=OB=2,AC=4,8分
∴S阴影=S△ABC-S△BOD-S扇形AOD=×4×4-×2×2-=8-2-π=6-π.12分
23.解析 (1)证明:如图,连结CO并延长交☉O于点G,连结BG,∵∠BAC=∠BCF,∠BGC=∠BAC,∴∠BCF=∠BGC,2分
∵CG是☉O的直径,∴∠GBC=90°,∴∠BGC+∠GCB=90°,∴∠BCF+∠GCB=90°,即∠GCF=90°,∴OC⊥CF,4分
∵OC为☉O的半径,∴CF为☉O的切线.5分
(2)∵AE为☉O的直径,AE⊥BC,BC=80 cm,∴BD=DC=BC=40 cm,6分
设☉O的半径为r cm,∴OD=(80-r)cm,
在Rt△ODC中,OD2+DC2=OC2,
∴(80-r)2+402=r2,
∴r=50,∴OC=50 cm,OD=30 cm,8分
∵∠DOC=∠COF,∠ODC=∠OCF=90°,
∴△ODC∽△OCF,10分
∴=,∴=,∴OF= cm,
∴风车中心O到地面F的距离为 cm.12分
24.解析 (1)y=-x2-2x+3.3分
(2)如图,连结OE.设E(n,-n2-2n+3),
∵点E在直线AC上方,∴n<0,-n2-2n+3>0,
∵A(-3,0),C(0,3),∴OA=OC=3,AC=3.
∵AC∥直线m,∴△ACH的面积是定值.4分
∵S四边形AECH=S△AEC+S△ACH,
∴当△AEC的面积最大时,四边形AECH的面积最大.5分
S△AEC=S△AEO+S△ECO-S△AOC=×3×(-n2-2n+3)+×3×(-n)-×3×3=-+.6分
∵-<0,∴n=-时,△AEC的面积最大,7分
∴E.8分
(3)存在.点Q的坐标为或或.14分
[详解]如图,由点P在x轴上,点Q在抛物线上,EF是平行四边形的边可知满足条件的点Q的纵坐标为±,
对于抛物线y=-x2-2x+3,当y=时,-x2-2x+3=,解得x=-(舍去)或x=-,∴Q1.
当y=-时,-x2-2x+3=-,解得x=,
∴Q2,Q3.
综上所述,满足条件的点Q的坐标为或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
