2024华东师大版数学九年级下学期课时练--专项素养综合全练(八)跨学科专题(二)(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--专项素养综合全练(八)跨学科专题(二)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 406.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 20:46:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
专项素养综合全练(八)
跨学科专题(二)
类型一 与生物学科融合
1.(2023重庆合川期末)棉花的纤维长度是棉花质量的重要指标.在甲、乙两类送检的棉花中各随机抽测了20朵棉花的纤维长度(单位:毫米),按从小到大的顺序排序结果如下:
甲:51,54,59,60,64,68,68,68,70,71,72,72,74,76,77,78,79,79,80,80.
乙:51,53,53,56,66,68,68,71,71,71,72,73,73,74,79,80,80,80,80,81.
根据以上数据绘制成统计表:
类型 平均数 众数 中位数 方差
甲 70 a 71.5 71.1
乙 70 80 b 90.1
(1)填空:a= ,b= ;
(2)若甲类棉花共有10 000朵,试估计甲类棉花的纤维长度不低于70毫米的数量;
(3)抽检员看了数据及统计表后认为甲类棉花纤维长度的稳定性更好,请结合所学知识和统计数据,写出支持检测员的结论的依据.
2.【项目式学习试题】【问题情境】大自然中的植物千姿百态,如果细心观察,就会发现:不同植物的叶子通常有着不同的特征,如果我们用数学的眼光来观察,会有什么发现呢 “数智”小组的四位同学开展了“利用树叶的特征对树木进行分类”的项目化学习活动.
【实践发现】同学们从收集的柳树叶、杨树叶中各随机选取10片,通过测量得到这些树叶的长和宽(单位:cm)的数据后,分别计算长宽比,整理数据如下:
序号 1 2 3 4 5 6 7 8 9 10
柳树叶的 长宽比 2 2.4 2.1 2.4 2.8 1.8 2.4 2.2 2.1 1.7
杨树叶的 长宽比 1.5 1.6 1.5 1.4 1.5 1.4 1.7 1.5 1.6 1.4
【实践探究】分析数据如下:
平均数 中位数 众数 方差
柳树叶的 长宽比 2.19 m 2.4 0.094 9
杨树叶的 长宽比 1.51 1.5 n 0.008 9
【问题解决】
(1)上述表格中:m= ,n= ;
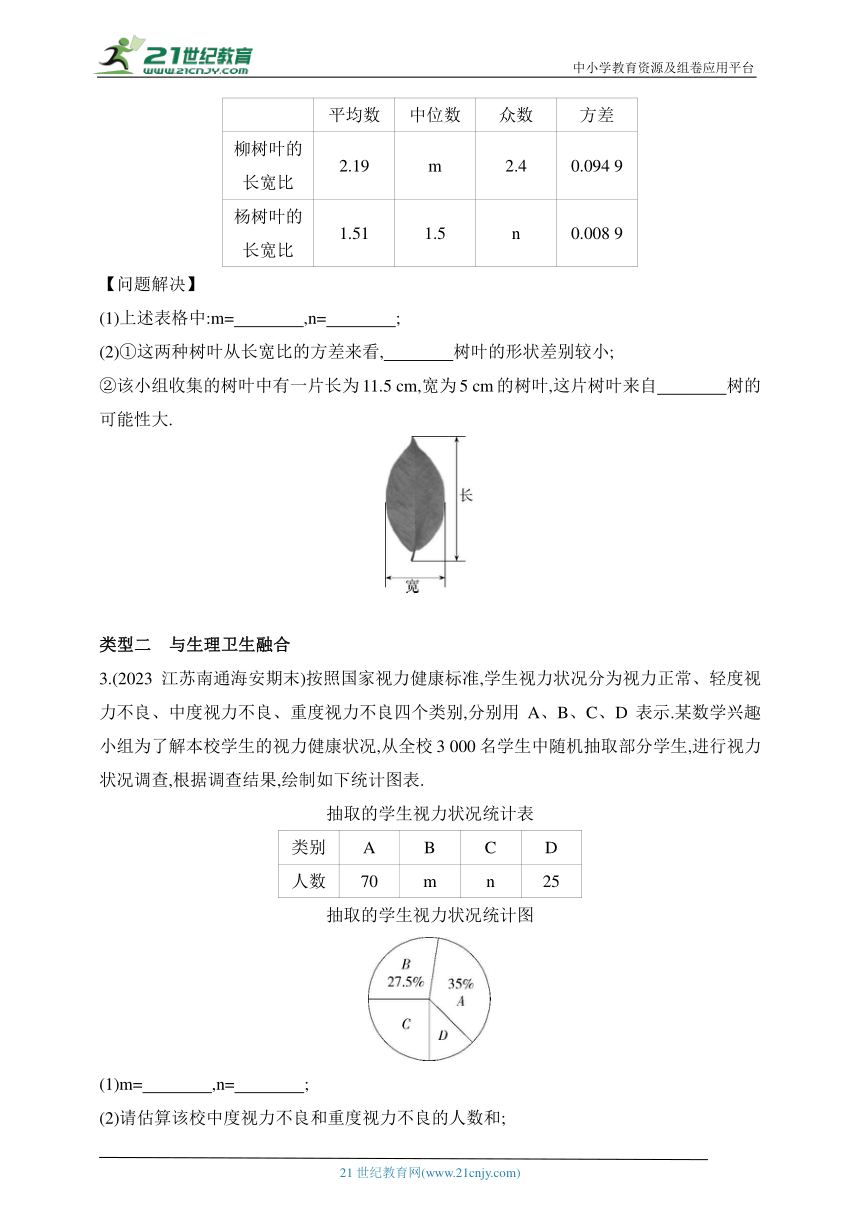
(2)①这两种树叶从长宽比的方差来看, 树叶的形状差别较小;
②该小组收集的树叶中有一片长为11.5 cm,宽为5 cm的树叶,这片树叶来自 树的可能性大.
类型二 与生理卫生融合
3.(2023江苏南通海安期末)按照国家视力健康标准,学生视力状况分为视力正常、轻度视力不良、中度视力不良、重度视力不良四个类别,分别用A、B、C、D表示.某数学兴趣小组为了解本校学生的视力健康状况,从全校3 000名学生中随机抽取部分学生,进行视力状况调查,根据调查结果,绘制如下统计图表.
抽取的学生视力状况统计表
类别 A B C D
人数 70 m n 25
抽取的学生视力状况统计图
(1)m= ,n= ;
(2)请估算该校中度视力不良和重度视力不良的人数和;
(3)为更好地保护视力,结合上述统计数据分析,请你提出一条合理化的建议.
类型三 与体育与健康学科融合
4.(2023广东实验中学模拟)某中学为了增强学生体质,决定开设以下体育课外活动项目:A.篮球,B.乒乓球,C.羽毛球,D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图.
试解答下列问题:
(1)求这次被调查的学生的人数;
(2)将条形统计图补充完整.
5.(2023江苏南京鼓楼期末)为了解全市中小学生体质健康情况,某市自2019年起,开展了多次全市范围的调查,以下是根据调查结果整理得到的部分信息.注:体测优秀率是指经测试,体质健康评定为“优秀”的学生占参加测试学生的总数的百分比.
(a)2019年和2022年全市四所重点监测学校学生体测优秀率统计图如图1.
(b)2019年和2022年全市中小学生体测优秀率按性别分类统计表如表:
2019年 2022年
男生 9.0% 11.1%
女生 3.4% 6.2%
(c)2005年以来全市中小学生体测优秀率统计图如图2.
根据以上信息,回答下列问题:
(1)四所重点监测学校中,从2019年到2022年,学生体测优秀率增幅最大的学校是 ,学生体测优秀率增速最快的学校是 ;
注:学生体测优秀率增幅=2022年学生体侧优秀率-2019年学生体测优秀率;学生体测优秀率增速=(2022年学生体侧优秀率-2019年学生体测优秀率)÷2019年学生体测优秀率.
(2)已知在2019年的调查样本中,男、女学生的比例约为1∶1,则2019年该市学生体测优秀率为 %(结果保留一位小数),由计算可知,在2022年的调查样本中,男生人数 女生人数(填“>”“<”或“=”);
(3)根据截至2022年的调查数据推断,你认为“2025年该市中小学生体测优秀率提升到10%以上”的目标能够实现吗 请说明理由.
答案全解全析
1.解析 (1)甲类的众数a=68,乙类的中位数b==71.5.
(2)10 000×=6 000,故甲类棉花的纤维长度不低于70毫米的数量约为6 000.
(3)∵甲类和乙类棉花纤维长度的平均值相同,甲的方差小于乙的方差,∴甲类棉花纤维长度的稳定性更好.
2.解析 (1)将柳树叶的长宽比从小到大排列,其中位数为=2.15,即m=2.15;杨树叶的长宽比的众数为1.5,即n=1.5.
(2)①因为杨树叶的长宽比的方差小于柳树叶的长宽比的方差,所以杨树叶的形状差别较小.
②长为11.5 cm,宽为5 cm的树叶的长宽比为2.3,而样本中杨树叶的长宽比都小于2.3,柳树叶的长宽比的众数为2.4,所以这片树叶来自柳树的可能性大.
3.解析 (1)70÷35%=200(人),m=200×27.5%=55,n=200-70-55-25=50.
(2)3 000×=1 125(人),故估算该校中度视力不良和重度视力不良的人数和为1 125.
(3)答案不唯一,如:该校学生视力正常的仅占35%,说明该校学生近视程度较为严重,建议学校加长学生户外运动时间.
4.解析 (1)20÷=200(人),故这次被调查的学生共有200人.
(2)最喜欢羽毛球的人数为200-20-80-40=60,补全统计图如下:
5.解析 (1)A学校从2019年到2022年学生体测优秀率增幅为26%-22%=4%,B学校从2019年到2022年学生体测优秀率增幅为25%-20%=5%,C学校从2019年到2022年学生体测优秀率增幅为15%-12%=3%,D学校从2019年到2022年学生体测优秀率增幅为8%-4%=4%,所以四所重点监测学校中,从2019年到2022年,学生体测优秀率增幅最大的学校是B.A学校从2019年到2022年学生体测优秀率增速为(26%-22%)÷22%×100%≈18.2%,B学校从2019年到2022年学生体测优秀率增速为(25%-20%)÷20%×100%=25%,C学校从2019年到2022年学生体测优秀率增速为(15%-12%)÷12%×100%=25%,D学校从2019年到2022年学生体测优秀率增速为(8%-4%)÷4%×100%=100%,所以四所重点监测学校中,从2019年到2022年,学生体测优秀率增速最快的学校是D.
(2)在2019年的调查样本中,男、女学生的比例约为1∶1,则2019年该市学生体测优秀率为=6.2%,若在2022年男、女学生的比例约为1∶1,则2022年该市学生体测优秀率为=8.65%,而2022年该市学生体测优秀率为8.50%,∵8.65%>8.50%,而男生优秀率为11.1%,女生优秀率为6.2%,
∴男生人数<女生人数.
(3)能实现.理由:从2014年到2022年这8年的平均年优秀率为(8.50%-3.30%)÷8=0.65%,∴从2022年到2025年这3年的优秀率为0.65%×3=1.95%,∵8.50%+1.95%=10.45%>10%,∴能实现目标.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
专项素养综合全练(八)
跨学科专题(二)
类型一 与生物学科融合
1.(2023重庆合川期末)棉花的纤维长度是棉花质量的重要指标.在甲、乙两类送检的棉花中各随机抽测了20朵棉花的纤维长度(单位:毫米),按从小到大的顺序排序结果如下:
甲:51,54,59,60,64,68,68,68,70,71,72,72,74,76,77,78,79,79,80,80.
乙:51,53,53,56,66,68,68,71,71,71,72,73,73,74,79,80,80,80,80,81.
根据以上数据绘制成统计表:
类型 平均数 众数 中位数 方差
甲 70 a 71.5 71.1
乙 70 80 b 90.1
(1)填空:a= ,b= ;
(2)若甲类棉花共有10 000朵,试估计甲类棉花的纤维长度不低于70毫米的数量;
(3)抽检员看了数据及统计表后认为甲类棉花纤维长度的稳定性更好,请结合所学知识和统计数据,写出支持检测员的结论的依据.
2.【项目式学习试题】【问题情境】大自然中的植物千姿百态,如果细心观察,就会发现:不同植物的叶子通常有着不同的特征,如果我们用数学的眼光来观察,会有什么发现呢 “数智”小组的四位同学开展了“利用树叶的特征对树木进行分类”的项目化学习活动.
【实践发现】同学们从收集的柳树叶、杨树叶中各随机选取10片,通过测量得到这些树叶的长和宽(单位:cm)的数据后,分别计算长宽比,整理数据如下:
序号 1 2 3 4 5 6 7 8 9 10
柳树叶的 长宽比 2 2.4 2.1 2.4 2.8 1.8 2.4 2.2 2.1 1.7
杨树叶的 长宽比 1.5 1.6 1.5 1.4 1.5 1.4 1.7 1.5 1.6 1.4
【实践探究】分析数据如下:
平均数 中位数 众数 方差
柳树叶的 长宽比 2.19 m 2.4 0.094 9
杨树叶的 长宽比 1.51 1.5 n 0.008 9
【问题解决】
(1)上述表格中:m= ,n= ;
(2)①这两种树叶从长宽比的方差来看, 树叶的形状差别较小;
②该小组收集的树叶中有一片长为11.5 cm,宽为5 cm的树叶,这片树叶来自 树的可能性大.
类型二 与生理卫生融合
3.(2023江苏南通海安期末)按照国家视力健康标准,学生视力状况分为视力正常、轻度视力不良、中度视力不良、重度视力不良四个类别,分别用A、B、C、D表示.某数学兴趣小组为了解本校学生的视力健康状况,从全校3 000名学生中随机抽取部分学生,进行视力状况调查,根据调查结果,绘制如下统计图表.
抽取的学生视力状况统计表
类别 A B C D
人数 70 m n 25
抽取的学生视力状况统计图
(1)m= ,n= ;
(2)请估算该校中度视力不良和重度视力不良的人数和;
(3)为更好地保护视力,结合上述统计数据分析,请你提出一条合理化的建议.
类型三 与体育与健康学科融合
4.(2023广东实验中学模拟)某中学为了增强学生体质,决定开设以下体育课外活动项目:A.篮球,B.乒乓球,C.羽毛球,D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图.
试解答下列问题:
(1)求这次被调查的学生的人数;
(2)将条形统计图补充完整.
5.(2023江苏南京鼓楼期末)为了解全市中小学生体质健康情况,某市自2019年起,开展了多次全市范围的调查,以下是根据调查结果整理得到的部分信息.注:体测优秀率是指经测试,体质健康评定为“优秀”的学生占参加测试学生的总数的百分比.
(a)2019年和2022年全市四所重点监测学校学生体测优秀率统计图如图1.
(b)2019年和2022年全市中小学生体测优秀率按性别分类统计表如表:
2019年 2022年
男生 9.0% 11.1%
女生 3.4% 6.2%
(c)2005年以来全市中小学生体测优秀率统计图如图2.
根据以上信息,回答下列问题:
(1)四所重点监测学校中,从2019年到2022年,学生体测优秀率增幅最大的学校是 ,学生体测优秀率增速最快的学校是 ;
注:学生体测优秀率增幅=2022年学生体侧优秀率-2019年学生体测优秀率;学生体测优秀率增速=(2022年学生体侧优秀率-2019年学生体测优秀率)÷2019年学生体测优秀率.
(2)已知在2019年的调查样本中,男、女学生的比例约为1∶1,则2019年该市学生体测优秀率为 %(结果保留一位小数),由计算可知,在2022年的调查样本中,男生人数 女生人数(填“>”“<”或“=”);
(3)根据截至2022年的调查数据推断,你认为“2025年该市中小学生体测优秀率提升到10%以上”的目标能够实现吗 请说明理由.
答案全解全析
1.解析 (1)甲类的众数a=68,乙类的中位数b==71.5.
(2)10 000×=6 000,故甲类棉花的纤维长度不低于70毫米的数量约为6 000.
(3)∵甲类和乙类棉花纤维长度的平均值相同,甲的方差小于乙的方差,∴甲类棉花纤维长度的稳定性更好.
2.解析 (1)将柳树叶的长宽比从小到大排列,其中位数为=2.15,即m=2.15;杨树叶的长宽比的众数为1.5,即n=1.5.
(2)①因为杨树叶的长宽比的方差小于柳树叶的长宽比的方差,所以杨树叶的形状差别较小.
②长为11.5 cm,宽为5 cm的树叶的长宽比为2.3,而样本中杨树叶的长宽比都小于2.3,柳树叶的长宽比的众数为2.4,所以这片树叶来自柳树的可能性大.
3.解析 (1)70÷35%=200(人),m=200×27.5%=55,n=200-70-55-25=50.
(2)3 000×=1 125(人),故估算该校中度视力不良和重度视力不良的人数和为1 125.
(3)答案不唯一,如:该校学生视力正常的仅占35%,说明该校学生近视程度较为严重,建议学校加长学生户外运动时间.
4.解析 (1)20÷=200(人),故这次被调查的学生共有200人.
(2)最喜欢羽毛球的人数为200-20-80-40=60,补全统计图如下:
5.解析 (1)A学校从2019年到2022年学生体测优秀率增幅为26%-22%=4%,B学校从2019年到2022年学生体测优秀率增幅为25%-20%=5%,C学校从2019年到2022年学生体测优秀率增幅为15%-12%=3%,D学校从2019年到2022年学生体测优秀率增幅为8%-4%=4%,所以四所重点监测学校中,从2019年到2022年,学生体测优秀率增幅最大的学校是B.A学校从2019年到2022年学生体测优秀率增速为(26%-22%)÷22%×100%≈18.2%,B学校从2019年到2022年学生体测优秀率增速为(25%-20%)÷20%×100%=25%,C学校从2019年到2022年学生体测优秀率增速为(15%-12%)÷12%×100%=25%,D学校从2019年到2022年学生体测优秀率增速为(8%-4%)÷4%×100%=100%,所以四所重点监测学校中,从2019年到2022年,学生体测优秀率增速最快的学校是D.
(2)在2019年的调查样本中,男、女学生的比例约为1∶1,则2019年该市学生体测优秀率为=6.2%,若在2022年男、女学生的比例约为1∶1,则2022年该市学生体测优秀率为=8.65%,而2022年该市学生体测优秀率为8.50%,∵8.65%>8.50%,而男生优秀率为11.1%,女生优秀率为6.2%,
∴男生人数<女生人数.
(3)能实现.理由:从2014年到2022年这8年的平均年优秀率为(8.50%-3.30%)÷8=0.65%,∴从2022年到2025年这3年的优秀率为0.65%×3=1.95%,∵8.50%+1.95%=10.45%>10%,∴能实现目标.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
