2024华东师大版数学九年级下学期课时练--专项素养综合全练(七)跨学科专题(一)(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--专项素养综合全练(七)跨学科专题(一)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 431.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
专项素养综合全练(七)
跨学科专题(一)
类型一 与地理融合
1.(2023河南洛阳第二外国语学校月考)数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28°纬线的长度.
小组成员查阅相关资料,得到如下信息:
信息一:在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图,赤道半径OA约为6 400千米,弦BC∥OA,以BC为直径的圆的周长就是北纬28°纬线的长度.
根据以上信息,北纬28°纬线的长度约为 千米.(参考数据:π≈3,sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53)
类型二 与体育与健康融合
2.(2023河南中考)小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.如图,在平面直角坐标系中,点A,C在x轴上,球网AB与y轴的水平距离OA=3 m,CA=2 m,击球点P在y轴上.若选择扣球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足一次函数关系y=-0.4x+2.8;若选择吊球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系y=a(x-1)2+3.2.
(1)求点P的坐标和a的值;
(2)小林分析发现,上面两种击球方式均能使球过网,要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
3.(2023甘肃兰州中考)一名运动员在10 m高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面OB的高度y(m)与离起跳点A的水平距离x(m)之间的函数关系如图所示,运动员离起跳点A的水平距离为1 m时达到最高点,当运动员离起跳点A的水平距离为3 m时离水面的距离为7 m.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离OB的长.
类型三 与生物融合
4.(2023山西大同模拟)生物学研究表明,在一定的温度范围内,酶的活性会随温度的升高逐渐增强;在最适温度时,酶的活性最强;超过一定温度范围,酶的活性又随温度的升高逐渐减弱,甚至会失去活性.现已知某种酶的活性值y(单位:IU)与温度x(单位:℃)的关系可以近似用二次函数y=-x2+14x+142来表示,则当温度为最适宜温度时,该种酶的活性值为 IU.
5.(2023贵州贵阳模拟)一个数学兴趣小组在上综合与实践课时发现:在大自然里,存在很多数学的奥秘,一片美丽的心形叶子、刚生长出的幼苗的部分轮廓线,可以近似地看作由抛物线的一部分沿直线折叠而成,如图①与图②所示.
【问题发现】如图③,为了确定一片心形叶子的形状,建立平面直角坐标系,发现心形叶子下方的轮廓线可以看作是二次函数y=mx2-4mx-20m+5图象的一部分,且过原点,求这个抛物线的表达式及顶点D的坐标.
【问题探究】如图③,心形叶片的对称轴直线y=x+2与坐标轴交于A,B两点,直线x=6分别交抛物线和直线AB于点E,F,点E、E'是叶片上的一对对称点,EE'交直线AB于点G.求叶片此处的宽度EE'的长.
【拓展应用】兴趣小组同学在观察某种幼苗生长的过程中,发现幼苗叶片下方轮廓线也可以看作是二次函数y=mx2-4mx-20m+5图象的一部分,如图④,幼苗叶片下方的轮廓线正好对应【问题发现】中的抛物线y=mx2-4mx-20m+5.若直线PD与水平线的夹角为45°,三天后,点D长到与点P同一水平位置的点D'时,叶尖Q落在射线OP上(如图⑤所示).求此时一片幼苗叶子的长度和最大宽度.
类型四 与信息科技融合
6.(2022湖北鄂州中考)某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)的图象.发现:如图1所示,该类型图象上任意一点M到定点F的距离MF,始终等于它到定直线l:y=-的距离MN(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=-叫做抛物线的准线方程,其中原点O为FH的中点,FH=2OF=.例如:抛物线y=x2,其焦点坐标为F,准线方程为l:y=-,其中MF=MN,FH=2OF=1.
【基础训练】
(1)请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程: ;
【技能训练】
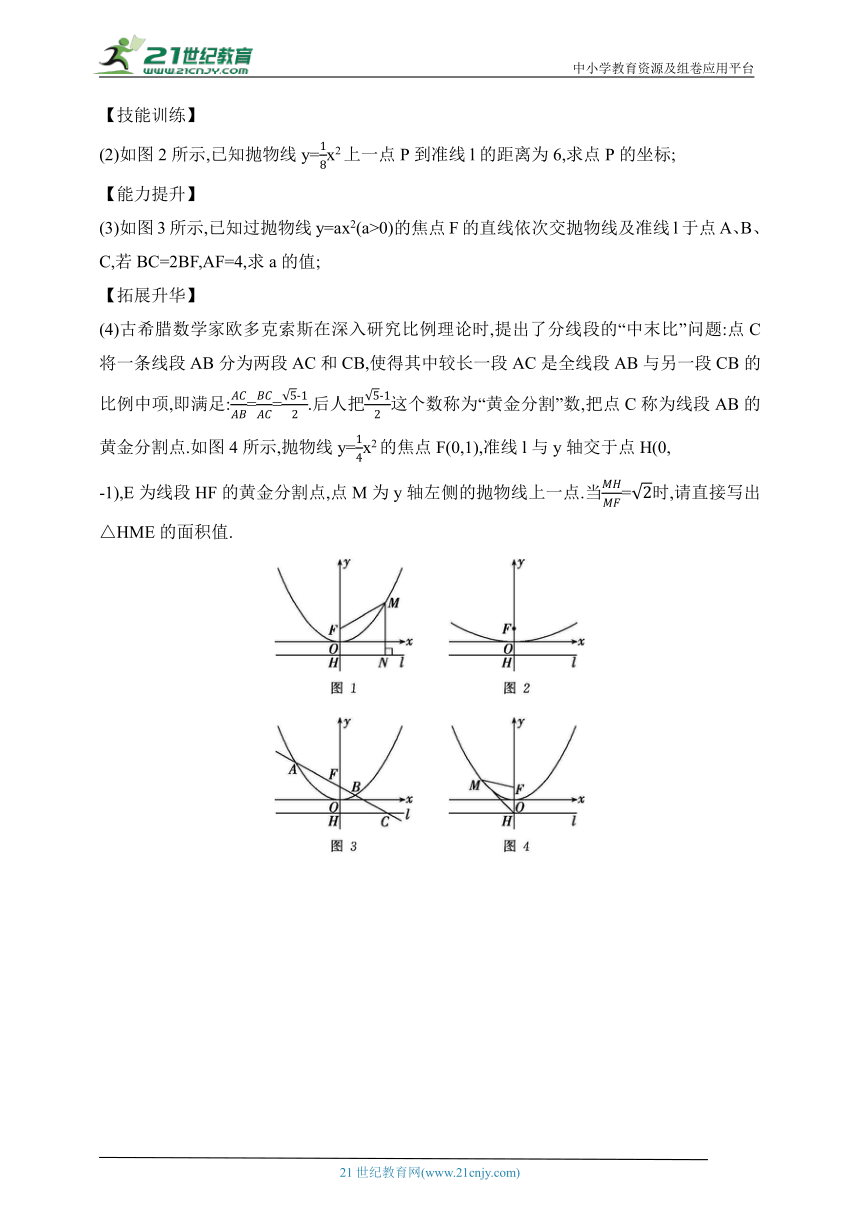
(2)如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标;
【能力提升】
(3)如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C,若BC=2BF,AF=4,求a的值;
【拓展升华】
(4)古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点C将一条线段AB分为两段AC和CB,使得其中较长一段AC是全线段AB与另一段CB的比例中项,即满足:==.后人把这个数称为“黄金分割”数,把点C称为线段AB的黄金分割点.如图4所示,抛物线y=x2的焦点F(0,1),准线l与y轴交于点H(0,
-1),E为线段HF的黄金分割点,点M为y轴左侧的抛物线上一点.当=时,请直接写出△HME的面积值.
答案全解全析
1.33 792
解析 如图,作OK⊥BC于K,则∠BKO=90°,
∵BC∥OA,∠AOB=28°,∴∠B=∠AOB=28°,在Rt△BOK中,OB=OA=
6 400千米,∴BK=OB·cos B≈6 400×0.88=5 632(千米),∴北纬28°纬线的长度=2π·BK≈2×3×5 632=33 792(千米).
2.解析 (1)在y=-0.4x+2.8中,令x=0,得y=2.8,∴点P的坐标为(0,2.8).
把P(0,2.8)代入y=a(x-1)2+3.2,得a+3.2=2.8,解得a=-0.4.
(2)∵OA=3 m,CA=2 m,∴OC=5 m,∴C(5,0),在y=-0.4x+2.8中,令y=0,得x=7,在y=-0.4(x-1)2+3.2中,令y=0,得-0.4(x-1)2+3.2=0,解得x=-2+1(舍去)或x=2+1≈3.83,∵|7-5|>|3.83-5|,∴选择吊球,球的落地点到C点的距离更近.
3.解析 (1)根据题意可得,抛物线过(0,10)和(3,7),对称轴为直线x=1,设y关于x的函数表达式为y=ax2+bx+c(a≠0),∴解得∴y关于x的函数表达式为y=-x2+2x+10.
(2)在y=-x2+2x+10中,令y=0,得0=-x2+2x+10,解得x=+1或x=
-+1(舍去),∴运动员从起跳点到入水点的水平距离OB的长为(+1)米.
4.240
解析 ∵y=-x2+14x+142=-(x-14)2+240,∴当x=14时,y的最大值为240,故当温度为14 ℃时,该种酶的活性值为240 IU.
5.解析 【问题发现】∵抛物线y=mx2-4mx-20m+5过原点,
∴-20m+5=0,解得m=,∴抛物线的表达式为y=x2-x=(x-2)2-1,
∴顶点D(2,-1).
【问题探究】当x=6时,y=x2-x=3,∴点E(6,3);当x=6时,y=x+2=8,
∴点F(6,8),∴EF=8-3=5,∵EF∥OB,∴∠GFE=∠ABO=45°,∵E,E'是叶片上的一对对称点,∴EE'=2EG,EG⊥FG,∴△EFG是等腰直角三角形,∴EG=EF=,∴EE'=2EG=5.
【拓展应用】如图,在QD'上取点M,过点M作MN∥y轴交抛物线于点N,交过点D'与x轴平行的直线于点L,过点N作NS⊥QD'于点S,由【问题发现】知点D(2,-1),∵直线PD与水平线的夹角为45°,∴直线PD的表达式为y=-x+1,联立解得或
∴点P(-2,3),∴点D'(2,3),将点D'的坐标代入y=mx2-4mx-20m+5得3=4m-8m-20m+5,解得m=,∴抛物线的表达式为y=x2-x+,由点P的坐标得直线OP的表达式为y=-x,联立解得或(舍去),∴点Q(-4,6),由点Q、D'的坐标得D'Q=3,yQD'=-x+4,即一片幼苗叶子的长度为3.设点M,则点Nx,x2-x+,∴MN=-x+4-=-(x+1)2+,
∴当x=-1时,MN的最大值为,由直线D'Q的表达式知,tan∠MD'L=,∴tan∠NMS=2,∴sin∠NMS=,∴一片幼苗叶子的最大宽度=2NS最大值=2×MN最大值·sin∠NMS=.
6.解析 (1);y=-.
(2)∵a=,∴-=-2,∴准线方程为y=-2,∴点P的纵坐标为4,∴x2=4,∴x=±4,∴点P的坐标为(4,4)或(-4,4).
(3)如图,作AG⊥l于G,作BK⊥l于K,∴AG=AF=4,BK=BF,FH=,∵BK∥FH∥AG,∴△CBK∽△CFH,△CBK∽△CAG,∴=,=,∴==,=,∴a=.
(4)设点M,∵=,∴=2,∴=2,
∴m1=-2,m2=2(舍去),∴M(-2,1),∵E为线段HF的黄金分割点,∴EH=FH=-1或EH=2-(-1)=3-,当EH=-1时,S△HME=EH·|xM|=×(-1)×2=-1;当EH=3-时,S△HME=×(3-)×2=3-,∴△HME的面积是-1或3-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
专项素养综合全练(七)
跨学科专题(一)
类型一 与地理融合
1.(2023河南洛阳第二外国语学校月考)数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28°纬线的长度.
小组成员查阅相关资料,得到如下信息:
信息一:在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图,赤道半径OA约为6 400千米,弦BC∥OA,以BC为直径的圆的周长就是北纬28°纬线的长度.
根据以上信息,北纬28°纬线的长度约为 千米.(参考数据:π≈3,sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53)
类型二 与体育与健康融合
2.(2023河南中考)小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.如图,在平面直角坐标系中,点A,C在x轴上,球网AB与y轴的水平距离OA=3 m,CA=2 m,击球点P在y轴上.若选择扣球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足一次函数关系y=-0.4x+2.8;若选择吊球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系y=a(x-1)2+3.2.
(1)求点P的坐标和a的值;
(2)小林分析发现,上面两种击球方式均能使球过网,要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
3.(2023甘肃兰州中考)一名运动员在10 m高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面OB的高度y(m)与离起跳点A的水平距离x(m)之间的函数关系如图所示,运动员离起跳点A的水平距离为1 m时达到最高点,当运动员离起跳点A的水平距离为3 m时离水面的距离为7 m.
(1)求y关于x的函数表达式;
(2)求运动员从起跳点到入水点的水平距离OB的长.
类型三 与生物融合
4.(2023山西大同模拟)生物学研究表明,在一定的温度范围内,酶的活性会随温度的升高逐渐增强;在最适温度时,酶的活性最强;超过一定温度范围,酶的活性又随温度的升高逐渐减弱,甚至会失去活性.现已知某种酶的活性值y(单位:IU)与温度x(单位:℃)的关系可以近似用二次函数y=-x2+14x+142来表示,则当温度为最适宜温度时,该种酶的活性值为 IU.
5.(2023贵州贵阳模拟)一个数学兴趣小组在上综合与实践课时发现:在大自然里,存在很多数学的奥秘,一片美丽的心形叶子、刚生长出的幼苗的部分轮廓线,可以近似地看作由抛物线的一部分沿直线折叠而成,如图①与图②所示.
【问题发现】如图③,为了确定一片心形叶子的形状,建立平面直角坐标系,发现心形叶子下方的轮廓线可以看作是二次函数y=mx2-4mx-20m+5图象的一部分,且过原点,求这个抛物线的表达式及顶点D的坐标.
【问题探究】如图③,心形叶片的对称轴直线y=x+2与坐标轴交于A,B两点,直线x=6分别交抛物线和直线AB于点E,F,点E、E'是叶片上的一对对称点,EE'交直线AB于点G.求叶片此处的宽度EE'的长.
【拓展应用】兴趣小组同学在观察某种幼苗生长的过程中,发现幼苗叶片下方轮廓线也可以看作是二次函数y=mx2-4mx-20m+5图象的一部分,如图④,幼苗叶片下方的轮廓线正好对应【问题发现】中的抛物线y=mx2-4mx-20m+5.若直线PD与水平线的夹角为45°,三天后,点D长到与点P同一水平位置的点D'时,叶尖Q落在射线OP上(如图⑤所示).求此时一片幼苗叶子的长度和最大宽度.
类型四 与信息科技融合
6.(2022湖北鄂州中考)某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)的图象.发现:如图1所示,该类型图象上任意一点M到定点F的距离MF,始终等于它到定直线l:y=-的距离MN(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=-叫做抛物线的准线方程,其中原点O为FH的中点,FH=2OF=.例如:抛物线y=x2,其焦点坐标为F,准线方程为l:y=-,其中MF=MN,FH=2OF=1.
【基础训练】
(1)请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程: ;
【技能训练】
(2)如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标;
【能力提升】
(3)如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C,若BC=2BF,AF=4,求a的值;
【拓展升华】
(4)古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点C将一条线段AB分为两段AC和CB,使得其中较长一段AC是全线段AB与另一段CB的比例中项,即满足:==.后人把这个数称为“黄金分割”数,把点C称为线段AB的黄金分割点.如图4所示,抛物线y=x2的焦点F(0,1),准线l与y轴交于点H(0,
-1),E为线段HF的黄金分割点,点M为y轴左侧的抛物线上一点.当=时,请直接写出△HME的面积值.
答案全解全析
1.33 792
解析 如图,作OK⊥BC于K,则∠BKO=90°,
∵BC∥OA,∠AOB=28°,∴∠B=∠AOB=28°,在Rt△BOK中,OB=OA=
6 400千米,∴BK=OB·cos B≈6 400×0.88=5 632(千米),∴北纬28°纬线的长度=2π·BK≈2×3×5 632=33 792(千米).
2.解析 (1)在y=-0.4x+2.8中,令x=0,得y=2.8,∴点P的坐标为(0,2.8).
把P(0,2.8)代入y=a(x-1)2+3.2,得a+3.2=2.8,解得a=-0.4.
(2)∵OA=3 m,CA=2 m,∴OC=5 m,∴C(5,0),在y=-0.4x+2.8中,令y=0,得x=7,在y=-0.4(x-1)2+3.2中,令y=0,得-0.4(x-1)2+3.2=0,解得x=-2+1(舍去)或x=2+1≈3.83,∵|7-5|>|3.83-5|,∴选择吊球,球的落地点到C点的距离更近.
3.解析 (1)根据题意可得,抛物线过(0,10)和(3,7),对称轴为直线x=1,设y关于x的函数表达式为y=ax2+bx+c(a≠0),∴解得∴y关于x的函数表达式为y=-x2+2x+10.
(2)在y=-x2+2x+10中,令y=0,得0=-x2+2x+10,解得x=+1或x=
-+1(舍去),∴运动员从起跳点到入水点的水平距离OB的长为(+1)米.
4.240
解析 ∵y=-x2+14x+142=-(x-14)2+240,∴当x=14时,y的最大值为240,故当温度为14 ℃时,该种酶的活性值为240 IU.
5.解析 【问题发现】∵抛物线y=mx2-4mx-20m+5过原点,
∴-20m+5=0,解得m=,∴抛物线的表达式为y=x2-x=(x-2)2-1,
∴顶点D(2,-1).
【问题探究】当x=6时,y=x2-x=3,∴点E(6,3);当x=6时,y=x+2=8,
∴点F(6,8),∴EF=8-3=5,∵EF∥OB,∴∠GFE=∠ABO=45°,∵E,E'是叶片上的一对对称点,∴EE'=2EG,EG⊥FG,∴△EFG是等腰直角三角形,∴EG=EF=,∴EE'=2EG=5.
【拓展应用】如图,在QD'上取点M,过点M作MN∥y轴交抛物线于点N,交过点D'与x轴平行的直线于点L,过点N作NS⊥QD'于点S,由【问题发现】知点D(2,-1),∵直线PD与水平线的夹角为45°,∴直线PD的表达式为y=-x+1,联立解得或
∴点P(-2,3),∴点D'(2,3),将点D'的坐标代入y=mx2-4mx-20m+5得3=4m-8m-20m+5,解得m=,∴抛物线的表达式为y=x2-x+,由点P的坐标得直线OP的表达式为y=-x,联立解得或(舍去),∴点Q(-4,6),由点Q、D'的坐标得D'Q=3,yQD'=-x+4,即一片幼苗叶子的长度为3.设点M,则点Nx,x2-x+,∴MN=-x+4-=-(x+1)2+,
∴当x=-1时,MN的最大值为,由直线D'Q的表达式知,tan∠MD'L=,∴tan∠NMS=2,∴sin∠NMS=,∴一片幼苗叶子的最大宽度=2NS最大值=2×MN最大值·sin∠NMS=.
6.解析 (1);y=-.
(2)∵a=,∴-=-2,∴准线方程为y=-2,∴点P的纵坐标为4,∴x2=4,∴x=±4,∴点P的坐标为(4,4)或(-4,4).
(3)如图,作AG⊥l于G,作BK⊥l于K,∴AG=AF=4,BK=BF,FH=,∵BK∥FH∥AG,∴△CBK∽△CFH,△CBK∽△CAG,∴=,=,∴==,=,∴a=.
(4)设点M,∵=,∴=2,∴=2,
∴m1=-2,m2=2(舍去),∴M(-2,1),∵E为线段HF的黄金分割点,∴EH=FH=-1或EH=2-(-1)=3-,当EH=-1时,S△HME=EH·|xM|=×(-1)×2=-1;当EH=3-时,S△HME=×(3-)×2=3-,∴△HME的面积是-1或3-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
