2024华东师大版数学九年级下学期课时练--专项素养综合全练(三)二次函数中的运动问题(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--专项素养综合全练(三)二次函数中的运动问题(含解析) | 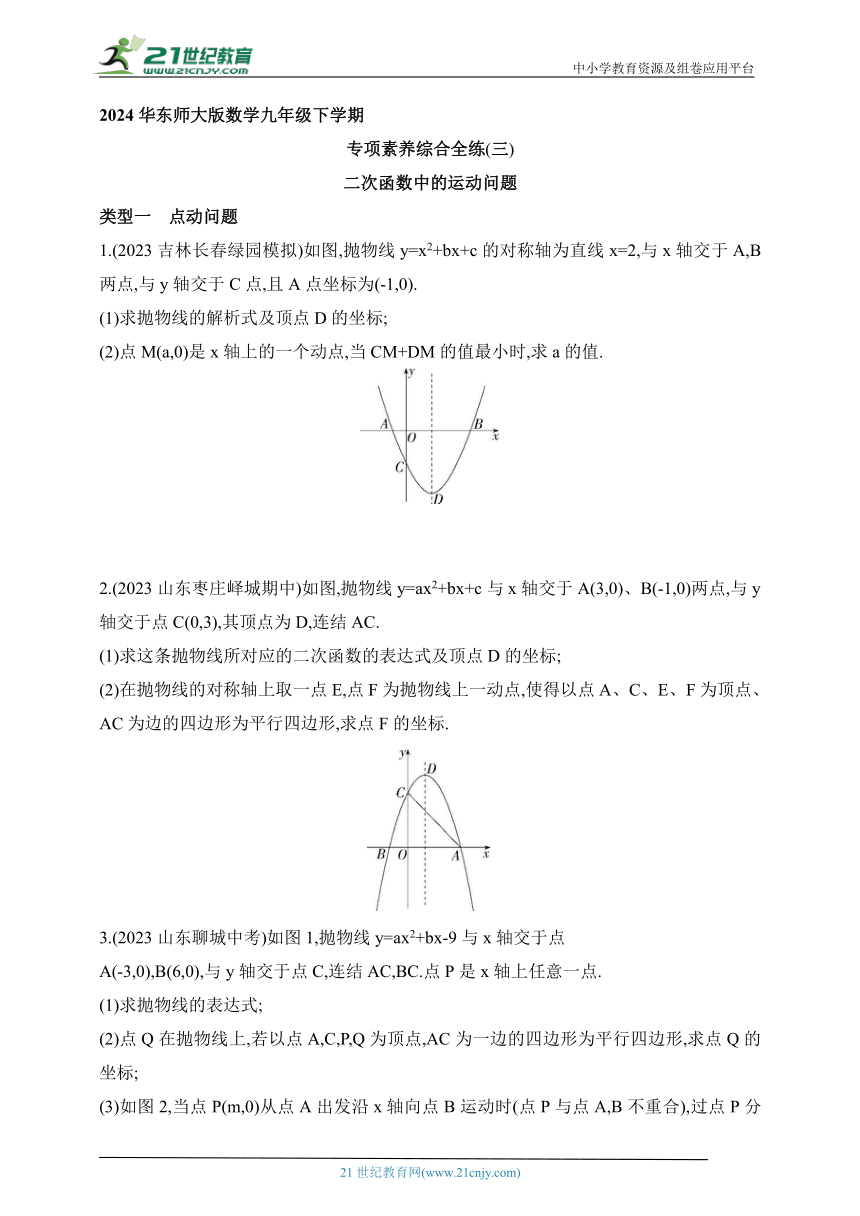 | |
| 格式 | docx | ||
| 文件大小 | 502.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 20:55:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
专项素养综合全练(三)
二次函数中的运动问题
类型一 点动问题
1.(2023吉林长春绿园模拟)如图,抛物线y=x2+bx+c的对称轴为直线x=2,与x轴交于A,B两点,与y轴交于C点,且A点坐标为(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点M(a,0)是x轴上的一个动点,当CM+DM的值最小时,求a的值.
2.(2023山东枣庄峄城期中)如图,抛物线y=ax2+bx+c与x轴交于A(3,0)、B(-1,0)两点,与y轴交于点C(0,3),其顶点为D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标.
3.(2023山东聊城中考)如图1,抛物线y=ax2+bx-9与x轴交于点
A(-3,0),B(6,0),与y轴交于点C,连结AC,BC.点P是x轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形,求点Q的坐标;
(3)如图2,当点P(m,0)从点A出发沿x轴向点B运动时(点P与点A,B不重合),过点P分别作PE∥BC,交AC于点E,PD⊥BC,垂足为点D,连结ED.当m为何值时,△PED的面积最大 并求出最大值.
类型二 线动问题
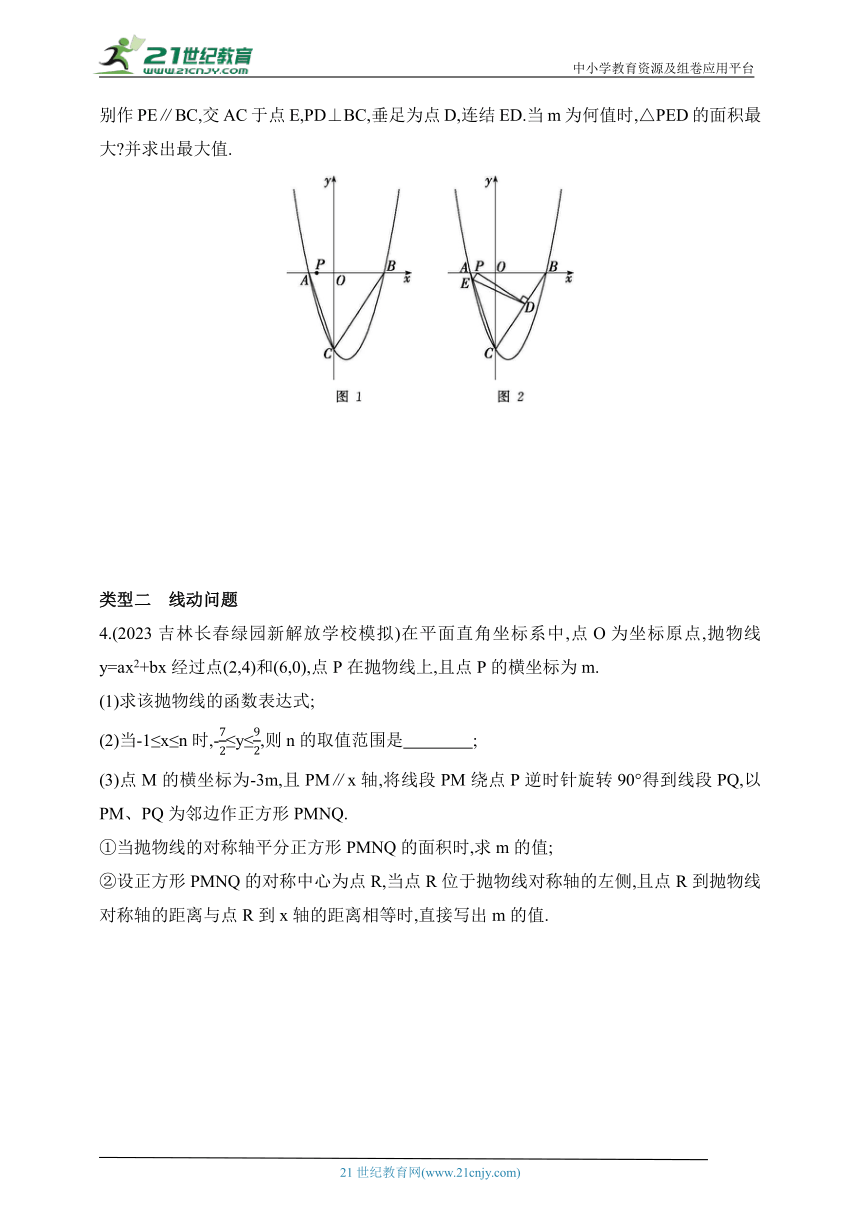
4.(2023吉林长春绿园新解放学校模拟)在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx经过点(2,4)和(6,0),点P在抛物线上,且点P的横坐标为m.
(1)求该抛物线的函数表达式;
(2)当-1≤x≤n时,-≤y≤,则n的取值范围是 ;
(3)点M的横坐标为-3m,且PM∥x轴,将线段PM绕点P逆时针旋转90°得到线段PQ,以PM、PQ为邻边作正方形PMNQ.
①当抛物线的对称轴平分正方形PMNQ的面积时,求m的值;
②设正方形PMNQ的对称中心为点R,当点R位于抛物线对称轴的左侧,且点R到抛物线对称轴的距离与点R到x轴的距离相等时,直接写出m的值.
5.(2023湖南衡阳中考)如图,已知抛物线y=ax2-2ax+3与x轴交于点A(-1,0)和点B,与y轴交于点C,连结AC,过B、C两点作直线.
(1)求a的值;
(2)将直线BC向下平移m(m>0)个单位长度,交抛物线于B'、C'两点,在直线B'C'上方的抛物线上是否存在定点D,使无论m取何值,都是点D到直线B'C'的距离最大 若存在,请求出点D的坐标,若不存在,请说明理由;
(3)抛物线上是否存在点P,使∠PBC+∠ACO=45° 若存在,请求出直线BP的解析式,若不存在,请说明理由.
类型三 形动问题
6.(2023吉林松原前郭南部学区模拟)如图1,在平面直角坐标系中,抛物线y=ax2-6ax+c与x轴交于点A和点B(5,0)(点A在点B左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)D为抛物线的顶点,点P在抛物线的对称轴上(不与点D重合),将线段PD绕点P按顺时针方向旋转90°,点D恰好落在抛物线上的点Q处,求点Q的坐标;
(3)如图2,将抛物线在x轴下方部分的图象沿x轴翻折到x轴上方,与原抛物线在x轴上方的部分图象组成新图象,再将新图象向左平移m个单位长度,若平移后的图象在-1≤x<0范围内,y随x的增大而增大,直接写出m的取值范围.
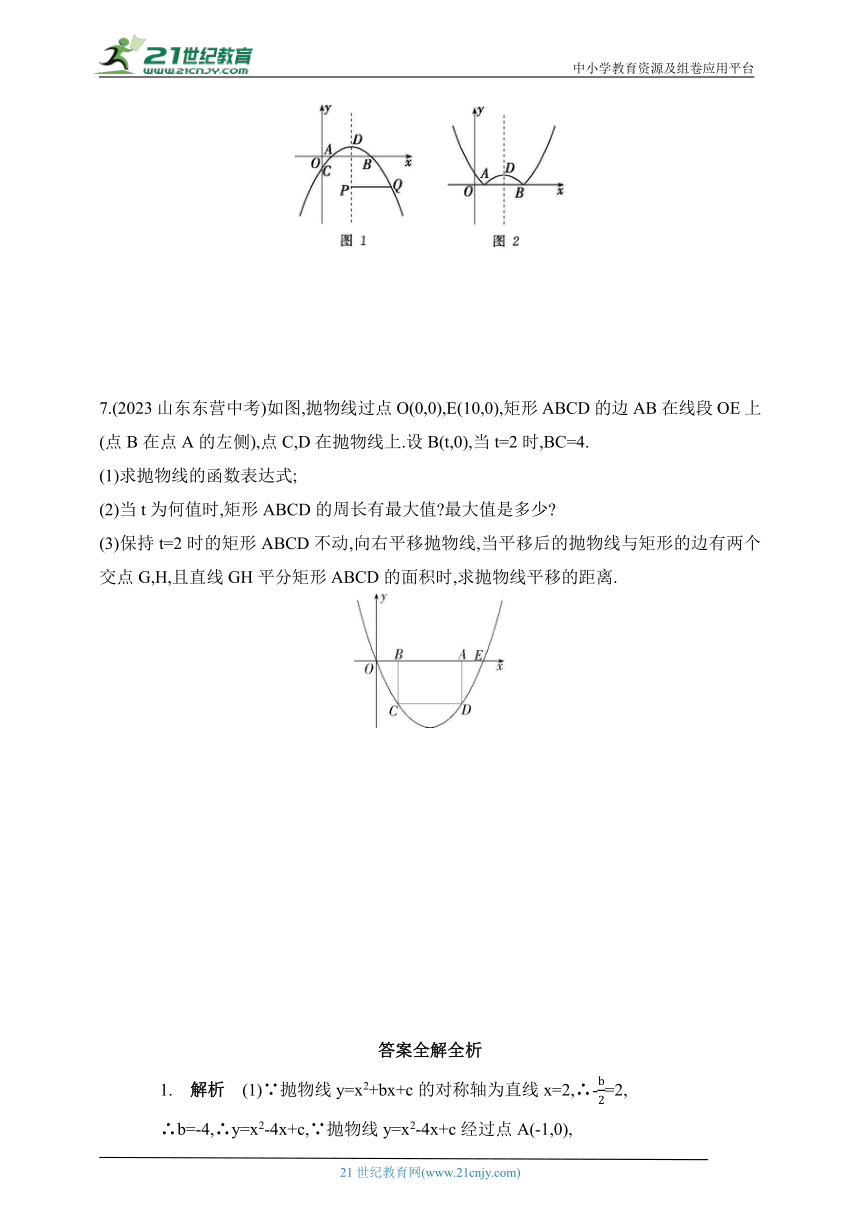
7.(2023山东东营中考)如图,抛物线过点O(0,0),E(10,0),矩形ABCD的边AB在线段OE上(点B在点A的左侧),点C,D在抛物线上.设B(t,0),当t=2时,BC=4.
(1)求抛物线的函数表达式;
(2)当t为何值时,矩形ABCD的周长有最大值 最大值是多少
(3)保持t=2时的矩形ABCD不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形ABCD的面积时,求抛物线平移的距离.
答案全解全析
解析 (1)∵抛物线y=x2+bx+c的对称轴为直线x=2,∴-=2,
∴b=-4,∴y=x2-4x+c,∵抛物线y=x2-4x+c经过点A(-1,0),
∴0=1+4+c,∴c=-5,∴抛物线的解析式为y=x2-4x-5,∵y=x2-4x-5=(x-2)2-9,∴抛物线的顶点D的坐标为(2,-9).
(2)如图,作点C关于x轴的对称点C',连结C'D交x轴于点M,连结CM,此时CM+DM的值最小,令x=0,则y=-5,∴点C的坐标为(0,-5),
∴点C'的坐标为(0,5),设直线C'D的解析式为y=mx+n(m≠0),∴解得∴直线C'D的解析式为y=-7x+5,令y=0,则-7x+5=0,解得x=,即直线C'D与x轴的交点M的坐标为,∴a=.
2.解析 (1)∵抛物线y=ax2+bx+c经过A(3,0),B(-1,0),C(0,3),∴解得∴抛物线的解析式为y=
-x2+2x+3,∵y=-x2+2x+3=-(x-1)2+4,∴顶点D的坐标为(1,4).
(2)设直线AC的解析式为y=kx+b(k≠0),把A(3,0),C(0,3)代入得∴∴直线AC的解析式为y=-x+3,如图,过点F作FG⊥DE于点G,∵以A、C、E、F为顶点、AC为边的四边形是平行四边形,∴AC=EF,AC∥EF,∵OA∥FG,∴∠OAC=∠GFE,∴△OAC≌△GFE,∴FG=OA=3,设F(m,-m2+2m+3),则G(1,-m2+2m+3),∴FG=|m-1|=3,∴m=-2或m=4,当m=-2时,-m2+2m+3=-5,∴F1(-2,-5),当m=4时,-m2+2m+3=
-5,∴F2(4,-5).综上所述,满足条件的点F的坐标为(-2,-5)或(4,-5).
3.解析 (1)结合题意设抛物线的表达式为y=a(x+3)(x-6),∴-9=a·3×
(-6),∴a=,∴y=(x+3)(x-6)=x2-x-9.
(2)如图,抛物线的对称轴为直线x==,由对称性可得点C(0,-9)关于对称轴对称的点Q1的坐标为(3,-9),当y=9时,即x2-x-9=9,解得x=,∴Q2,Q3,综上所述,点Q的坐标为(3,-9)或,9或.
(3)设△PED的面积为S,由题意得AP=m+3,BP=6-m,OB=6,OC=9,AB=9,∴BC==3,∵sin∠PBD==,∴=,∴PD=,∵PE∥BC,∴△APE∽△ABC,∠EPD=∠PDB=90°,∴=,∴=,∴PE=,∴S△PED=PE·PD=(m+3)(6-m)=-+,∵-<0,∴当m=时,S取得最大值,即△PDE的面积最大,最大值为.
4.解析 (1)将点(2,4)和(6,0)代入y=ax2+bx得解得∴该抛物线的函数表达式为y=-x2+3x.
(2)y=-x2+3x=-(x-3)2+,对称轴为直线x=3,顶点为,令y=-,解得x1=-1,x2=7,画该函数图象如下,
∵当-1≤x≤n时,-≤y≤,∴结合函数图象可知3≤n≤7.
(3)①如图,∵抛物线的对称轴平分正方形PMNQ的面积,平分正方形的面积的直线要过它的对称中心,且PM∥x轴,∴对称轴即直线x=3是线段PM的垂直平分线,∵点P的横坐标为m,点M的横坐标为
-3m,∴=3,解得m=-3,即m的值为-3.
②如图,∵点P的横坐标为m,点M的横坐标为-3m,∴R的横坐标是=-m,∵点R位于抛物线对称轴的左侧,对称轴为直线x=3,∴-m<3,即m>-3,∵点P在抛物线上,∴设P,∴M-3m,-m2+3m,∵线段PM绕点P逆时针旋转90°得到线段PQ,∴Qm,
-m2+3m+(-3m-m),即Qm,-m2-m,易知R是MQ的中点,∴R-m,
-m2+m,∴点R到抛物线对称轴的距离为3-(-m)=3+m,点R到x轴的距离为,∵点R到抛物线对称轴的距离与点R到x轴的距离相等,∴3+m=,解得m1=2+,m2=2-,即m的值为2+或2-.
5.解析 (1)∵抛物线y=ax2-2ax+3与x轴交于点
A(-1,0),∴a+2a+3=0,∴a=-1.
(2)存在定点D,使无论m取何值,都是点D到直线B'C'的距离最大.理由如下:∵y=-x2+2x+3,当x=0时,y=3,∴C(0,3),当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,∴B(3,0),设直线BC的解析式为y=kx+b(k≠0),则解得∴直线BC的解析式为y=-x+3,∵将直线BC向下平移m(m>0)个单位长度,交抛物线于B'、C'两点,∴直线B'C'的解析式为y=-x+3-m,设D(t,-t2+2t+3),过点D作DE∥y轴,交B'C'于点E,作DF⊥B'C'于点F,设直线B'C'交y轴于点G,如图,
∴E(t,-t+3-m),∴DE=-t2+2t+3-(-t+3-m)=-t2+3t+m,∵OB=OC=3,∠BOC=90°,∴∠BCO=∠CBO=45°,∵B'C'∥BC,
∴∠B'GO=∠BCO=45°,∵DE∥y轴,∴∠DEF=∠B'GO=45°,∵∠DFE=90°,∴△DEF是等腰直角三角形,∴DF=DE=(-t2+3t+m)=-+,∵-<0,∴当t=时,DF取得最大值,最大值为,此时点D的坐标为.
(3)存在,直线BP的解析式为y=-x+1或y=-3x+9.分情况求解如下:
①当∠PBC在直线BC的下方时,在y轴正半轴上取点M(0,1),连结BM并延长交抛物线于点P,如图1,∵A(-1,0),B(3,0),C(0,3),M(0,1),∴OB=OC=3,OM=OA=1,∠BOM=∠COA=90°,∴△BOM≌△COA,∴∠MBO=∠ACO,∵∠CBO=45°,∴∠PBC+∠MBO=45°,∴∠PBC+∠ACO=45°,设直线BM的解析式为y=k'x+b'(k'≠0),则解得∴直线BM的解析式为y=-x+1,联立解得(舍去),∴P.
②当∠PBC在直线BC的上方时,作点M关于直线BC的对称点M',如图2,连结MM',CM',直线BM'交抛物线于P,由对称得∠PBC=∠MBC,MM'⊥BC,CM'=CM=2,∠BCM'=∠BCM=45°,∴∠PBC+
∠ACO=∠MBC+∠OBM=45°,∠MCM'=90°,∴M'(2,3),则直线BM'的解析式为y=-3x+9,联立解得(舍去),∴P(2,3).
综上所述,抛物线上存在点P,使∠PBC+∠ACO=45°,直线BP的解析式为y=-x+1或y=-3x+9.
6.解析 (1)将点B(5,0)、C分别代入抛物线y=ax2-6ax+c,得解得故抛物线的解析式为y=-x2+x-.
(2)∵y=-x2+x-=-(x-3)2+1,∴D(3,1).设点P(3,m),∵PQ=PD=1-m,∴Q(3+1-m,m),即Q(4-m,m),将其代入抛物线解析式,得m=-(4-m)2+(4-m)-,整理得m2+2m-3=0,∴(m-1)(m+3)=0,∴m=1或-3,∴P(3,1)或P(3,-3).∵点P不与点D重合,∴m=-3,∴点Q的坐标为(7,-3).
(3)2≤m≤3或m≥6.详解:∵当y=0时,x=1或5,∴A(1,0).根据题图2的图象可知,在AD段和点B的右侧,y随x的增大而增大.新图象向左平移m个单位后,A(1-m,0),B(5-m,0),D(3-m,1).平移后的图象在-1≤x<0范围内,y随x的增大而增大,当AD段平移到1≤x<0范围内时,1-m≤-1,3-m≥0,∴2≤m≤3.当B点右侧平移到-1≤x<0范围内时,5-m≤-1,即m≥6,∴2≤m≤3或m≥6.
7.解析 (1)设抛物线解析式为y=ax(x-10),∵当t=2时,BC=4,∴点C的坐标为(2,-4),∴将点C坐标代入解析式得2a(2-10)=-4,解得a=,
∴抛物线的函数表达式为y=x2-x.
(2)由抛物线的对称性得AE=OB=t,∴AB=10-2t,当x=t时,点C的纵坐标为t2-t,∴矩形ABCD的周长=2(AB+BC)=2(10-2t)+=-t2+t+20=-(t-1)2+,∵-<0,∴当t=1时,矩形ABCD的周长有最大值,最大值为.
(3)如图,连结AC,BD相交于点P,连结OC,取OC的中点Q,连结PQ,GH,
∵直线GH平分矩形ABCD的面积,∴直线GH过点P,由平移的性质可知,PQ∥OA,∴△CQP∽△COA,∵四边形ABCD是矩形,∴点P是AC的中点,∴PQ=OA,∴抛物线平移的距离是4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
专项素养综合全练(三)
二次函数中的运动问题
类型一 点动问题
1.(2023吉林长春绿园模拟)如图,抛物线y=x2+bx+c的对称轴为直线x=2,与x轴交于A,B两点,与y轴交于C点,且A点坐标为(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)点M(a,0)是x轴上的一个动点,当CM+DM的值最小时,求a的值.
2.(2023山东枣庄峄城期中)如图,抛物线y=ax2+bx+c与x轴交于A(3,0)、B(-1,0)两点,与y轴交于点C(0,3),其顶点为D,连结AC.
(1)求这条抛物线所对应的二次函数的表达式及顶点D的坐标;
(2)在抛物线的对称轴上取一点E,点F为抛物线上一动点,使得以点A、C、E、F为顶点、AC为边的四边形为平行四边形,求点F的坐标.
3.(2023山东聊城中考)如图1,抛物线y=ax2+bx-9与x轴交于点
A(-3,0),B(6,0),与y轴交于点C,连结AC,BC.点P是x轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,若以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形,求点Q的坐标;
(3)如图2,当点P(m,0)从点A出发沿x轴向点B运动时(点P与点A,B不重合),过点P分别作PE∥BC,交AC于点E,PD⊥BC,垂足为点D,连结ED.当m为何值时,△PED的面积最大 并求出最大值.
类型二 线动问题
4.(2023吉林长春绿园新解放学校模拟)在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx经过点(2,4)和(6,0),点P在抛物线上,且点P的横坐标为m.
(1)求该抛物线的函数表达式;
(2)当-1≤x≤n时,-≤y≤,则n的取值范围是 ;
(3)点M的横坐标为-3m,且PM∥x轴,将线段PM绕点P逆时针旋转90°得到线段PQ,以PM、PQ为邻边作正方形PMNQ.
①当抛物线的对称轴平分正方形PMNQ的面积时,求m的值;
②设正方形PMNQ的对称中心为点R,当点R位于抛物线对称轴的左侧,且点R到抛物线对称轴的距离与点R到x轴的距离相等时,直接写出m的值.
5.(2023湖南衡阳中考)如图,已知抛物线y=ax2-2ax+3与x轴交于点A(-1,0)和点B,与y轴交于点C,连结AC,过B、C两点作直线.
(1)求a的值;
(2)将直线BC向下平移m(m>0)个单位长度,交抛物线于B'、C'两点,在直线B'C'上方的抛物线上是否存在定点D,使无论m取何值,都是点D到直线B'C'的距离最大 若存在,请求出点D的坐标,若不存在,请说明理由;
(3)抛物线上是否存在点P,使∠PBC+∠ACO=45° 若存在,请求出直线BP的解析式,若不存在,请说明理由.
类型三 形动问题
6.(2023吉林松原前郭南部学区模拟)如图1,在平面直角坐标系中,抛物线y=ax2-6ax+c与x轴交于点A和点B(5,0)(点A在点B左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)D为抛物线的顶点,点P在抛物线的对称轴上(不与点D重合),将线段PD绕点P按顺时针方向旋转90°,点D恰好落在抛物线上的点Q处,求点Q的坐标;
(3)如图2,将抛物线在x轴下方部分的图象沿x轴翻折到x轴上方,与原抛物线在x轴上方的部分图象组成新图象,再将新图象向左平移m个单位长度,若平移后的图象在-1≤x<0范围内,y随x的增大而增大,直接写出m的取值范围.
7.(2023山东东营中考)如图,抛物线过点O(0,0),E(10,0),矩形ABCD的边AB在线段OE上(点B在点A的左侧),点C,D在抛物线上.设B(t,0),当t=2时,BC=4.
(1)求抛物线的函数表达式;
(2)当t为何值时,矩形ABCD的周长有最大值 最大值是多少
(3)保持t=2时的矩形ABCD不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形ABCD的面积时,求抛物线平移的距离.
答案全解全析
解析 (1)∵抛物线y=x2+bx+c的对称轴为直线x=2,∴-=2,
∴b=-4,∴y=x2-4x+c,∵抛物线y=x2-4x+c经过点A(-1,0),
∴0=1+4+c,∴c=-5,∴抛物线的解析式为y=x2-4x-5,∵y=x2-4x-5=(x-2)2-9,∴抛物线的顶点D的坐标为(2,-9).
(2)如图,作点C关于x轴的对称点C',连结C'D交x轴于点M,连结CM,此时CM+DM的值最小,令x=0,则y=-5,∴点C的坐标为(0,-5),
∴点C'的坐标为(0,5),设直线C'D的解析式为y=mx+n(m≠0),∴解得∴直线C'D的解析式为y=-7x+5,令y=0,则-7x+5=0,解得x=,即直线C'D与x轴的交点M的坐标为,∴a=.
2.解析 (1)∵抛物线y=ax2+bx+c经过A(3,0),B(-1,0),C(0,3),∴解得∴抛物线的解析式为y=
-x2+2x+3,∵y=-x2+2x+3=-(x-1)2+4,∴顶点D的坐标为(1,4).
(2)设直线AC的解析式为y=kx+b(k≠0),把A(3,0),C(0,3)代入得∴∴直线AC的解析式为y=-x+3,如图,过点F作FG⊥DE于点G,∵以A、C、E、F为顶点、AC为边的四边形是平行四边形,∴AC=EF,AC∥EF,∵OA∥FG,∴∠OAC=∠GFE,∴△OAC≌△GFE,∴FG=OA=3,设F(m,-m2+2m+3),则G(1,-m2+2m+3),∴FG=|m-1|=3,∴m=-2或m=4,当m=-2时,-m2+2m+3=-5,∴F1(-2,-5),当m=4时,-m2+2m+3=
-5,∴F2(4,-5).综上所述,满足条件的点F的坐标为(-2,-5)或(4,-5).
3.解析 (1)结合题意设抛物线的表达式为y=a(x+3)(x-6),∴-9=a·3×
(-6),∴a=,∴y=(x+3)(x-6)=x2-x-9.
(2)如图,抛物线的对称轴为直线x==,由对称性可得点C(0,-9)关于对称轴对称的点Q1的坐标为(3,-9),当y=9时,即x2-x-9=9,解得x=,∴Q2,Q3,综上所述,点Q的坐标为(3,-9)或,9或.
(3)设△PED的面积为S,由题意得AP=m+3,BP=6-m,OB=6,OC=9,AB=9,∴BC==3,∵sin∠PBD==,∴=,∴PD=,∵PE∥BC,∴△APE∽△ABC,∠EPD=∠PDB=90°,∴=,∴=,∴PE=,∴S△PED=PE·PD=(m+3)(6-m)=-+,∵-<0,∴当m=时,S取得最大值,即△PDE的面积最大,最大值为.
4.解析 (1)将点(2,4)和(6,0)代入y=ax2+bx得解得∴该抛物线的函数表达式为y=-x2+3x.
(2)y=-x2+3x=-(x-3)2+,对称轴为直线x=3,顶点为,令y=-,解得x1=-1,x2=7,画该函数图象如下,
∵当-1≤x≤n时,-≤y≤,∴结合函数图象可知3≤n≤7.
(3)①如图,∵抛物线的对称轴平分正方形PMNQ的面积,平分正方形的面积的直线要过它的对称中心,且PM∥x轴,∴对称轴即直线x=3是线段PM的垂直平分线,∵点P的横坐标为m,点M的横坐标为
-3m,∴=3,解得m=-3,即m的值为-3.
②如图,∵点P的横坐标为m,点M的横坐标为-3m,∴R的横坐标是=-m,∵点R位于抛物线对称轴的左侧,对称轴为直线x=3,∴-m<3,即m>-3,∵点P在抛物线上,∴设P,∴M-3m,-m2+3m,∵线段PM绕点P逆时针旋转90°得到线段PQ,∴Qm,
-m2+3m+(-3m-m),即Qm,-m2-m,易知R是MQ的中点,∴R-m,
-m2+m,∴点R到抛物线对称轴的距离为3-(-m)=3+m,点R到x轴的距离为,∵点R到抛物线对称轴的距离与点R到x轴的距离相等,∴3+m=,解得m1=2+,m2=2-,即m的值为2+或2-.
5.解析 (1)∵抛物线y=ax2-2ax+3与x轴交于点
A(-1,0),∴a+2a+3=0,∴a=-1.
(2)存在定点D,使无论m取何值,都是点D到直线B'C'的距离最大.理由如下:∵y=-x2+2x+3,当x=0时,y=3,∴C(0,3),当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,∴B(3,0),设直线BC的解析式为y=kx+b(k≠0),则解得∴直线BC的解析式为y=-x+3,∵将直线BC向下平移m(m>0)个单位长度,交抛物线于B'、C'两点,∴直线B'C'的解析式为y=-x+3-m,设D(t,-t2+2t+3),过点D作DE∥y轴,交B'C'于点E,作DF⊥B'C'于点F,设直线B'C'交y轴于点G,如图,
∴E(t,-t+3-m),∴DE=-t2+2t+3-(-t+3-m)=-t2+3t+m,∵OB=OC=3,∠BOC=90°,∴∠BCO=∠CBO=45°,∵B'C'∥BC,
∴∠B'GO=∠BCO=45°,∵DE∥y轴,∴∠DEF=∠B'GO=45°,∵∠DFE=90°,∴△DEF是等腰直角三角形,∴DF=DE=(-t2+3t+m)=-+,∵-<0,∴当t=时,DF取得最大值,最大值为,此时点D的坐标为.
(3)存在,直线BP的解析式为y=-x+1或y=-3x+9.分情况求解如下:
①当∠PBC在直线BC的下方时,在y轴正半轴上取点M(0,1),连结BM并延长交抛物线于点P,如图1,∵A(-1,0),B(3,0),C(0,3),M(0,1),∴OB=OC=3,OM=OA=1,∠BOM=∠COA=90°,∴△BOM≌△COA,∴∠MBO=∠ACO,∵∠CBO=45°,∴∠PBC+∠MBO=45°,∴∠PBC+∠ACO=45°,设直线BM的解析式为y=k'x+b'(k'≠0),则解得∴直线BM的解析式为y=-x+1,联立解得(舍去),∴P.
②当∠PBC在直线BC的上方时,作点M关于直线BC的对称点M',如图2,连结MM',CM',直线BM'交抛物线于P,由对称得∠PBC=∠MBC,MM'⊥BC,CM'=CM=2,∠BCM'=∠BCM=45°,∴∠PBC+
∠ACO=∠MBC+∠OBM=45°,∠MCM'=90°,∴M'(2,3),则直线BM'的解析式为y=-3x+9,联立解得(舍去),∴P(2,3).
综上所述,抛物线上存在点P,使∠PBC+∠ACO=45°,直线BP的解析式为y=-x+1或y=-3x+9.
6.解析 (1)将点B(5,0)、C分别代入抛物线y=ax2-6ax+c,得解得故抛物线的解析式为y=-x2+x-.
(2)∵y=-x2+x-=-(x-3)2+1,∴D(3,1).设点P(3,m),∵PQ=PD=1-m,∴Q(3+1-m,m),即Q(4-m,m),将其代入抛物线解析式,得m=-(4-m)2+(4-m)-,整理得m2+2m-3=0,∴(m-1)(m+3)=0,∴m=1或-3,∴P(3,1)或P(3,-3).∵点P不与点D重合,∴m=-3,∴点Q的坐标为(7,-3).
(3)2≤m≤3或m≥6.详解:∵当y=0时,x=1或5,∴A(1,0).根据题图2的图象可知,在AD段和点B的右侧,y随x的增大而增大.新图象向左平移m个单位后,A(1-m,0),B(5-m,0),D(3-m,1).平移后的图象在-1≤x<0范围内,y随x的增大而增大,当AD段平移到1≤x<0范围内时,1-m≤-1,3-m≥0,∴2≤m≤3.当B点右侧平移到-1≤x<0范围内时,5-m≤-1,即m≥6,∴2≤m≤3或m≥6.
7.解析 (1)设抛物线解析式为y=ax(x-10),∵当t=2时,BC=4,∴点C的坐标为(2,-4),∴将点C坐标代入解析式得2a(2-10)=-4,解得a=,
∴抛物线的函数表达式为y=x2-x.
(2)由抛物线的对称性得AE=OB=t,∴AB=10-2t,当x=t时,点C的纵坐标为t2-t,∴矩形ABCD的周长=2(AB+BC)=2(10-2t)+=-t2+t+20=-(t-1)2+,∵-<0,∴当t=1时,矩形ABCD的周长有最大值,最大值为.
(3)如图,连结AC,BD相交于点P,连结OC,取OC的中点Q,连结PQ,GH,
∵直线GH平分矩形ABCD的面积,∴直线GH过点P,由平移的性质可知,PQ∥OA,∴△CQP∽△COA,∵四边形ABCD是矩形,∴点P是AC的中点,∴PQ=OA,∴抛物线平移的距离是4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
