2024华东师大版数学九年级下学期课时练--专项素养综合全练(二)二次函数最值的应用(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--专项素养综合全练(二)二次函数最值的应用(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
专项素养综合全练(二)
二次函数最值的应用
类型一 求高度的最值
1.(2023福建漳州康桥学校期末)如图,一小球M从斜坡OA上的O点处抛出,建立如图所示的平面直角坐标系,球的抛出路线是抛物线L1:y=-x2+bx的一部分,斜坡可以看作直线L2:y=x的一部分.若小球经过点(6,6),解答下列问题:
(1)求抛物线L1的表达式,并直接写出抛物线L1的对称轴;
(2)小球在斜坡上的落点为A,求A点的坐标;
(3)在斜坡OA上的B点有一棵树,B点的横坐标为2,树高为4,小球M能否飞过这棵树 通过计算说明理由;
(4)直接写出小球M在飞行的过程中离斜坡OA的最大高度.
类型二 求几何图形面积的最值
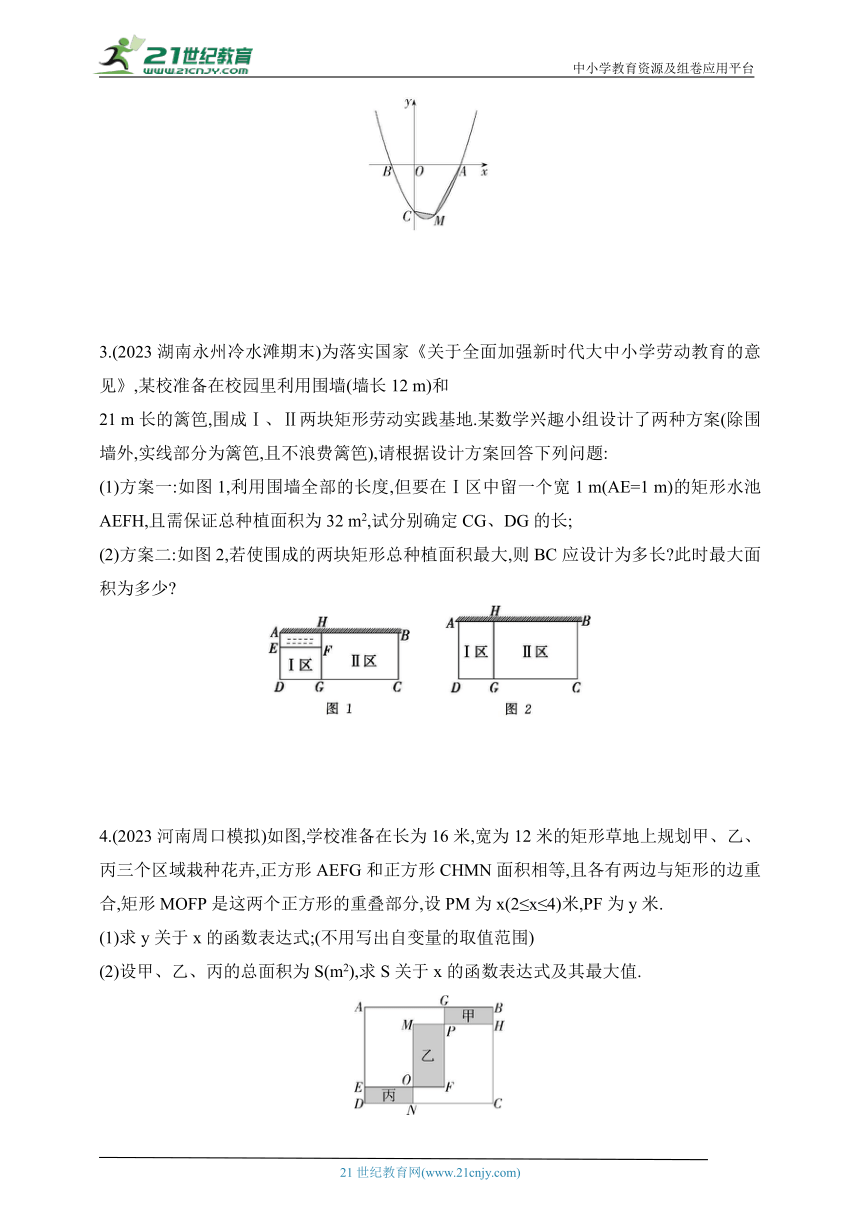
2.(2023安徽黄山休宁洪里中学期中)如图,已知抛物线过点A(4,0),
B(-2,0),C(0,-4).
(1)求抛物线的解析式;
(2)如图,点M是抛物线AC段上的一个动点,当图中阴影部分的面积最小时,求点M的坐标.
3.(2023湖南永州冷水滩期末)为落实国家《关于全面加强新时代大中小学劳动教育的意见》,某校准备在校园里利用围墙(墙长12 m)和
21 m长的篱笆,围成Ⅰ、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案(除围墙外,实线部分为篱笆,且不浪费篱笆),请根据设计方案回答下列问题:
(1)方案一:如图1,利用围墙全部的长度,但要在Ⅰ区中留一个宽1 m(AE=1 m)的矩形水池AEFH,且需保证总种植面积为32 m2,试分别确定CG、DG的长;
(2)方案二:如图2,若使围成的两块矩形总种植面积最大,则BC应设计为多长 此时最大面积为多少
4.(2023河南周口模拟)如图,学校准备在长为16米,宽为12米的矩形草地上规划甲、乙、丙三个区域栽种花卉,正方形AEFG和正方形CHMN面积相等,且各有两边与矩形的边重合,矩形MOFP是这两个正方形的重叠部分,设PM为x(2≤x≤4)米,PF为y米.
(1)求y关于x的函数表达式;(不用写出自变量的取值范围)
(2)设甲、乙、丙的总面积为S(m2),求S关于x的函数表达式及其最大值.
类型三 求销售类问题的最值
5.(2023湖北仙桃中考)某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表(1≤x≤60,x为整数):
第x天 1≤x≤30 31≤x≤60
日销售价(元/件) 0.5x+35 50
日销售量(件) 124-2x
设该商品的日销售利润为w元.
(1)直接写出w与x的函数关系式;
(2)该商品第几天的日销售利润最多 最多日销售利润是多少
6.(2023内蒙古包头中考)随着科技的发展,扫地机器人(图1)已广泛应用于生活中.某公司推出一款新型扫地机器人,统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化.设该产品2022年x(x为整数)月每台的销售价格为y元,y与x的函数关系如图2所示(图中ABC为折线).
(1)当1≤x≤10时,求每台的销售价格y与x之间的函数关系式;
(2)设该产品2022年第x个月的销售量为m万台,m与x的关系可以用m=x+1来描述,求哪个月的销售收入最多,最多为多少万元.(销售收入=每台的销售价格×销售量)
7.(2023湖北十堰中考)“端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进某品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒.根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒.设每盒售价为x元,日销售量为p盒.
(1)当x=60时,p= ;
(2)当每盒售价定为多少元时,日销售利润W(元)最大 最大利润是多少
(3)小强说:“当日销售利润最大时,日销售额不是最大.”小红说:“当日销售利润不低于8 000元时,每盒售价x的取值范围为60≤x≤80.”你认为他们的说法正确吗 若正确,请说明理由;若不正确,请直接写出正确的结论.
答案全解全析
1.解析 (1)把点(6,6)代入L1:y=-x2+bx得6=-×62+6b,解得b=4,∴抛物线L1的解析式为y=-x2+4x,∵y=-x2+4x=-(x-4)2+8,∴抛物线L1的对称轴为直线x=4.
(2)联立解得或∴A点的坐标为.
(3)小球M能飞过这棵树,理由如下:当x=2时,y=×2=1,y=-×22+4×2=6,6-1=5>4,∴小球M能飞过这棵树.
(4)根据题意得小球M在飞行的过程中离斜坡OA的距离为-x2+4x-x=-x2+x=-+,∵-<0,∴小球M在飞行的过程中离斜坡OA的最大高度为.
2.解析 (1)设抛物线解析式为y=a(x+2)(x-4),把C(0,-4)代入得a·2×
(-4)=-4,解得a=,∴抛物线解析式为y=(x+2)(x-4),即y=x2-x-4.
(2)如图,连结AC,则AC与抛物线所围成的图形的面积为定值,当△ACM的面积最大时,图中阴影部分的面积最小,作MN∥y轴交AC于N,设M,由A(4,0),C(0,-4)知线段AC所在直线的解析式为y=x-4,则N(x,x-4),∴MN=x-4-=-x2+2x,∴S△ACM=S△MNC+S△MNA=×4MN=-x2+4x=-(x-2)2+4,当x=2时,△ACM的面积最大,图中阴影部分的面积最小,此时点M的坐标为(2,-4).
3.解析 (1)∵(21-12)÷3=3(m),∴Ⅰ、Ⅱ两块矩形的面积之和为12×3=36(m2),设水池的长EF为a m,则水池的面积为a×1=a(m2),∴36-a=32,解得a=4,∴DG=EF=4 m,∴CG=CD-DG=12-4=8(m),故CG的长为8 m,DG的长为4 m.
(2)设BC的长为x m,则CD的长为(21-3x)m,∴总种植面积为(21-3x)·x=-3(x2-7x)=+,∵-3<0,∴当x=时,总种植面积最大,最大为 m2,故BC应设计为 m,此时最大面积为 m2.
4.解析 (1)由题可知,AG+MH=16+PM,AE+MN=12+PF,∴16+PM=12+PF,即16+x=12+y,∴y=x+4.
(2)∵正方形AEFG和正方形CHMN的面积相等,∴AG=MH,∴2AG=16+x,
∴S正方形AEFG=S正方形CHMN=,又S乙=xy=x(x+4),∴S=S甲+S乙+S丙=16×12-(S正方形AEFG+S正方形CHMN-2S乙)=16×12-2+2x(x+4),整理得S=x2-8x+64=+64-,∵>0,故当x>时,S随x的增大而增大,当x<时,S随x的增大而减小,∵>,∴当x=4时,S取得最大值,S最大=×42-8×4+64=56.
5.解析 (1)当1≤x≤30时,w=(0.5x+35-30)·(-2x+124)=-x2+52x+620.当31≤x≤60时,w=(50-30)(-2x+124)=-40x+2 480,∴w与x的函数关系式为w=
(2)当1≤x≤30时,w=-x2+52x+620=-(x-26)2+1 296,∵-1<0,∴当x=26时,w有最大值,最大值为1 296;当31≤x≤60时,w=-40x+2 480,
∵-40<0,∴当x=31时,w有最大值,最大值为-40×31+2 480=1 240,
∵1 296>1 240,∴该商品第26天的日销售利润最多,最多日销售利润是1 296元.
6.解析 (1)当1≤x≤10时,设每台的销售价格y与x之间的函数关系式为y=kx+b(k≠0),∵图象过A(1,2 850),B(10,1 500)两点,∴解得∴当1≤x≤10时,每台的销售价格y与x之间的函数关系式为y=-150x+3 000.
(2)设销售收入为w万元,
①当1≤x≤10时,w=(-150x+3 000)=-15(x-5)2+3 375,
∵-15<0,∴当x=5时,w有最大值,w最大=3 375;
②当100,∴当x=12时,w有最大值,w最大=150×12+1 500=3 300.
∵3 375>3 300,∴5月的销售收入最多,最多为3 375万元.
7.解析 (1)由题意可得p=500-10(x-50)=-10x+1 000,即日销售量p(盒)与每盒售价x(元)之间的函数关系式是p=-10x+1 000,当x=60时,
p=-10×60+1 000=400.
(2)由题意可得W=(x-40)(-10x+1 000)=-10x2+1 400x-40 000=-10(x-70)2+9 000,由题意可知即解得50≤x≤65,∵-10<0,∴当x=65时,W取得最大值,此时W=-10×(65-70)2+9 000=8 750,故当每盒售价定为65元时,日销售利润W(元)最大,最大利润是8 750元.
(3)小强:设日销售额为y元,则y=x·p=x(-10x+1 000)=-10x2+1 000x=
-10(x-50)2+25 000,∵-10<0,50≤x≤65,∴当x=50时,y取得最大值,此时y=25 000,由(2)知,当x=65时,W取得最大值,∴小强正确.
小红错误,当日销售利润不低于8 000元时,每盒售价x的取值范围为60≤x≤65.详解:当日销售利润不低于8 000元时,即-10(x-70)2+9 000≥
8 000,解得60≤x≤80,∵50≤x≤65,∴当日销售利润不低于8 000元时,每盒售价x的取值范围为60≤x≤65,∴小红错误.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
专项素养综合全练(二)
二次函数最值的应用
类型一 求高度的最值
1.(2023福建漳州康桥学校期末)如图,一小球M从斜坡OA上的O点处抛出,建立如图所示的平面直角坐标系,球的抛出路线是抛物线L1:y=-x2+bx的一部分,斜坡可以看作直线L2:y=x的一部分.若小球经过点(6,6),解答下列问题:
(1)求抛物线L1的表达式,并直接写出抛物线L1的对称轴;
(2)小球在斜坡上的落点为A,求A点的坐标;
(3)在斜坡OA上的B点有一棵树,B点的横坐标为2,树高为4,小球M能否飞过这棵树 通过计算说明理由;
(4)直接写出小球M在飞行的过程中离斜坡OA的最大高度.
类型二 求几何图形面积的最值
2.(2023安徽黄山休宁洪里中学期中)如图,已知抛物线过点A(4,0),
B(-2,0),C(0,-4).
(1)求抛物线的解析式;
(2)如图,点M是抛物线AC段上的一个动点,当图中阴影部分的面积最小时,求点M的坐标.
3.(2023湖南永州冷水滩期末)为落实国家《关于全面加强新时代大中小学劳动教育的意见》,某校准备在校园里利用围墙(墙长12 m)和
21 m长的篱笆,围成Ⅰ、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案(除围墙外,实线部分为篱笆,且不浪费篱笆),请根据设计方案回答下列问题:
(1)方案一:如图1,利用围墙全部的长度,但要在Ⅰ区中留一个宽1 m(AE=1 m)的矩形水池AEFH,且需保证总种植面积为32 m2,试分别确定CG、DG的长;
(2)方案二:如图2,若使围成的两块矩形总种植面积最大,则BC应设计为多长 此时最大面积为多少
4.(2023河南周口模拟)如图,学校准备在长为16米,宽为12米的矩形草地上规划甲、乙、丙三个区域栽种花卉,正方形AEFG和正方形CHMN面积相等,且各有两边与矩形的边重合,矩形MOFP是这两个正方形的重叠部分,设PM为x(2≤x≤4)米,PF为y米.
(1)求y关于x的函数表达式;(不用写出自变量的取值范围)
(2)设甲、乙、丙的总面积为S(m2),求S关于x的函数表达式及其最大值.
类型三 求销售类问题的最值
5.(2023湖北仙桃中考)某商店销售某种商品的进价为每件30元,这种商品在近60天中的日销售价与日销售量的相关信息如下表(1≤x≤60,x为整数):
第x天 1≤x≤30 31≤x≤60
日销售价(元/件) 0.5x+35 50
日销售量(件) 124-2x
设该商品的日销售利润为w元.
(1)直接写出w与x的函数关系式;
(2)该商品第几天的日销售利润最多 最多日销售利润是多少
6.(2023内蒙古包头中考)随着科技的发展,扫地机器人(图1)已广泛应用于生活中.某公司推出一款新型扫地机器人,统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化.设该产品2022年x(x为整数)月每台的销售价格为y元,y与x的函数关系如图2所示(图中ABC为折线).
(1)当1≤x≤10时,求每台的销售价格y与x之间的函数关系式;
(2)设该产品2022年第x个月的销售量为m万台,m与x的关系可以用m=x+1来描述,求哪个月的销售收入最多,最多为多少万元.(销售收入=每台的销售价格×销售量)
7.(2023湖北十堰中考)“端午节”吃粽子是中国传统习俗,在“端午节”来临前,某超市购进某品牌粽子,每盒进价是40元,并规定每盒售价不得少于50元,日销售量不低于350盒.根据以往销售经验发现,当每盒售价定为50元时,日销售量为500盒,每盒售价每提高1元,日销售量减少10盒.设每盒售价为x元,日销售量为p盒.
(1)当x=60时,p= ;
(2)当每盒售价定为多少元时,日销售利润W(元)最大 最大利润是多少
(3)小强说:“当日销售利润最大时,日销售额不是最大.”小红说:“当日销售利润不低于8 000元时,每盒售价x的取值范围为60≤x≤80.”你认为他们的说法正确吗 若正确,请说明理由;若不正确,请直接写出正确的结论.
答案全解全析
1.解析 (1)把点(6,6)代入L1:y=-x2+bx得6=-×62+6b,解得b=4,∴抛物线L1的解析式为y=-x2+4x,∵y=-x2+4x=-(x-4)2+8,∴抛物线L1的对称轴为直线x=4.
(2)联立解得或∴A点的坐标为.
(3)小球M能飞过这棵树,理由如下:当x=2时,y=×2=1,y=-×22+4×2=6,6-1=5>4,∴小球M能飞过这棵树.
(4)根据题意得小球M在飞行的过程中离斜坡OA的距离为-x2+4x-x=-x2+x=-+,∵-<0,∴小球M在飞行的过程中离斜坡OA的最大高度为.
2.解析 (1)设抛物线解析式为y=a(x+2)(x-4),把C(0,-4)代入得a·2×
(-4)=-4,解得a=,∴抛物线解析式为y=(x+2)(x-4),即y=x2-x-4.
(2)如图,连结AC,则AC与抛物线所围成的图形的面积为定值,当△ACM的面积最大时,图中阴影部分的面积最小,作MN∥y轴交AC于N,设M,由A(4,0),C(0,-4)知线段AC所在直线的解析式为y=x-4,则N(x,x-4),∴MN=x-4-=-x2+2x,∴S△ACM=S△MNC+S△MNA=×4MN=-x2+4x=-(x-2)2+4,当x=2时,△ACM的面积最大,图中阴影部分的面积最小,此时点M的坐标为(2,-4).
3.解析 (1)∵(21-12)÷3=3(m),∴Ⅰ、Ⅱ两块矩形的面积之和为12×3=36(m2),设水池的长EF为a m,则水池的面积为a×1=a(m2),∴36-a=32,解得a=4,∴DG=EF=4 m,∴CG=CD-DG=12-4=8(m),故CG的长为8 m,DG的长为4 m.
(2)设BC的长为x m,则CD的长为(21-3x)m,∴总种植面积为(21-3x)·x=-3(x2-7x)=+,∵-3<0,∴当x=时,总种植面积最大,最大为 m2,故BC应设计为 m,此时最大面积为 m2.
4.解析 (1)由题可知,AG+MH=16+PM,AE+MN=12+PF,∴16+PM=12+PF,即16+x=12+y,∴y=x+4.
(2)∵正方形AEFG和正方形CHMN的面积相等,∴AG=MH,∴2AG=16+x,
∴S正方形AEFG=S正方形CHMN=,又S乙=xy=x(x+4),∴S=S甲+S乙+S丙=16×12-(S正方形AEFG+S正方形CHMN-2S乙)=16×12-2+2x(x+4),整理得S=x2-8x+64=+64-,∵>0,故当x>时,S随x的增大而增大,当x<时,S随x的增大而减小,∵>,∴当x=4时,S取得最大值,S最大=×42-8×4+64=56.
5.解析 (1)当1≤x≤30时,w=(0.5x+35-30)·(-2x+124)=-x2+52x+620.当31≤x≤60时,w=(50-30)(-2x+124)=-40x+2 480,∴w与x的函数关系式为w=
(2)当1≤x≤30时,w=-x2+52x+620=-(x-26)2+1 296,∵-1<0,∴当x=26时,w有最大值,最大值为1 296;当31≤x≤60时,w=-40x+2 480,
∵-40<0,∴当x=31时,w有最大值,最大值为-40×31+2 480=1 240,
∵1 296>1 240,∴该商品第26天的日销售利润最多,最多日销售利润是1 296元.
6.解析 (1)当1≤x≤10时,设每台的销售价格y与x之间的函数关系式为y=kx+b(k≠0),∵图象过A(1,2 850),B(10,1 500)两点,∴解得∴当1≤x≤10时,每台的销售价格y与x之间的函数关系式为y=-150x+3 000.
(2)设销售收入为w万元,
①当1≤x≤10时,w=(-150x+3 000)=-15(x-5)2+3 375,
∵-15<0,∴当x=5时,w有最大值,w最大=3 375;
②当10
∵3 375>3 300,∴5月的销售收入最多,最多为3 375万元.
7.解析 (1)由题意可得p=500-10(x-50)=-10x+1 000,即日销售量p(盒)与每盒售价x(元)之间的函数关系式是p=-10x+1 000,当x=60时,
p=-10×60+1 000=400.
(2)由题意可得W=(x-40)(-10x+1 000)=-10x2+1 400x-40 000=-10(x-70)2+9 000,由题意可知即解得50≤x≤65,∵-10<0,∴当x=65时,W取得最大值,此时W=-10×(65-70)2+9 000=8 750,故当每盒售价定为65元时,日销售利润W(元)最大,最大利润是8 750元.
(3)小强:设日销售额为y元,则y=x·p=x(-10x+1 000)=-10x2+1 000x=
-10(x-50)2+25 000,∵-10<0,50≤x≤65,∴当x=50时,y取得最大值,此时y=25 000,由(2)知,当x=65时,W取得最大值,∴小强正确.
小红错误,当日销售利润不低于8 000元时,每盒售价x的取值范围为60≤x≤65.详解:当日销售利润不低于8 000元时,即-10(x-70)2+9 000≥
8 000,解得60≤x≤80,∵50≤x≤65,∴当日销售利润不低于8 000元时,每盒售价x的取值范围为60≤x≤65,∴小红错误.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
