2024华东师大版数学九年级下学期课时练--专项素养综合全练(一)二次函数表达式的三种常见求解方法(含解析)
文档属性
| 名称 | 2024华东师大版数学九年级下学期课时练--专项素养综合全练(一)二次函数表达式的三种常见求解方法(含解析) | 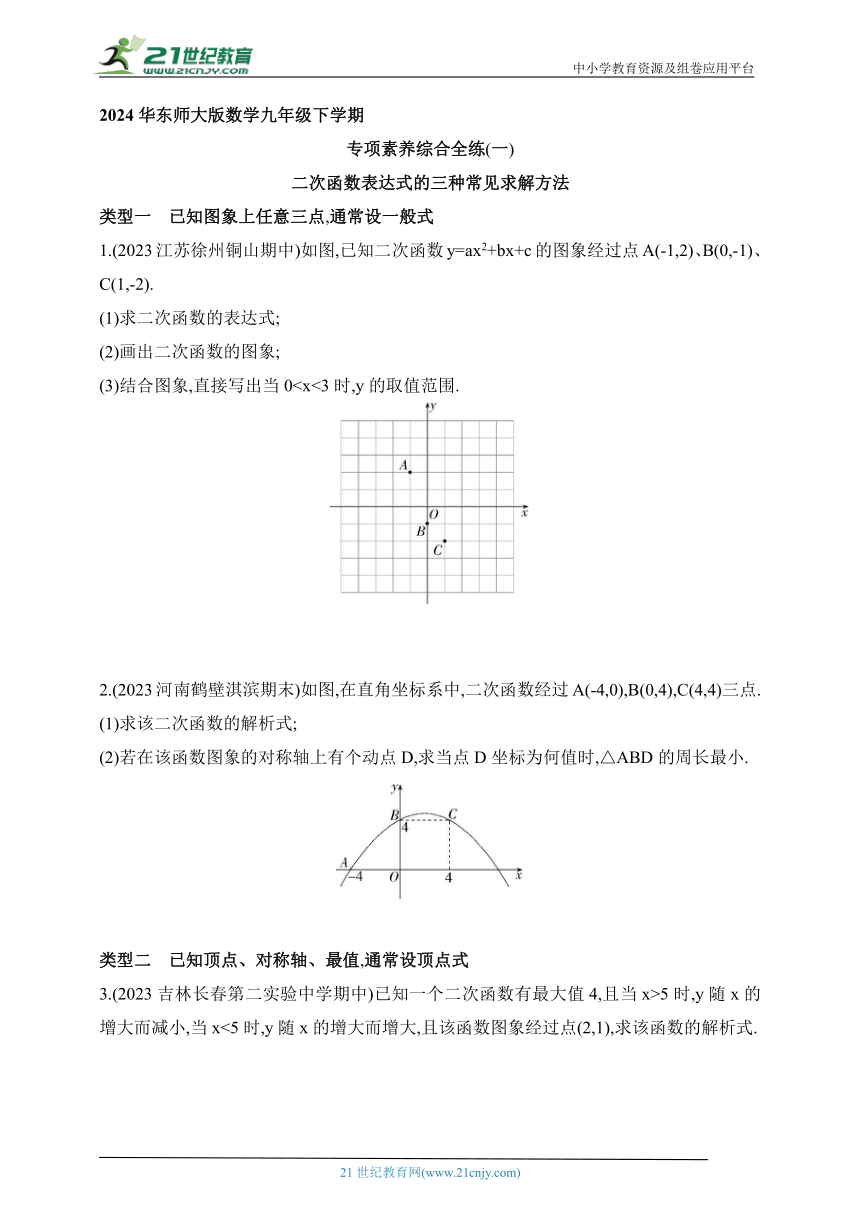 | |
| 格式 | docx | ||
| 文件大小 | 385.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 20:59:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学九年级下学期
专项素养综合全练(一)
二次函数表达式的三种常见求解方法
类型一 已知图象上任意三点,通常设一般式
1.(2023江苏徐州铜山期中)如图,已知二次函数y=ax2+bx+c的图象经过点A(-1,2)、B(0,-1)、C(1,-2).
(1)求二次函数的表达式;
(2)画出二次函数的图象;
(3)结合图象,直接写出当02.(2023河南鹤壁淇滨期末)如图,在直角坐标系中,二次函数经过A(-4,0),B(0,4),C(4,4)三点.
(1)求该二次函数的解析式;
(2)若在该函数图象的对称轴上有个动点D,求当点D坐标为何值时,△ABD的周长最小.
类型二 已知顶点、对称轴、最值,通常设顶点式
3.(2023吉林长春第二实验中学期中)已知一个二次函数有最大值4,且当x>5时,y随x的增大而减小,当x<5时,y随x的增大而增大,且该函数图象经过点(2,1),求该函数的解析式.
4.(2023河南周口淮阳模拟)已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x … -4 -3 -2 -1 0 1 2 …
y … -5 0 3 4 3 m -5 …
(1)根据表格,直接写出该二次函数的对称轴以及m的值;
(2)求该二次函数的表达式.
5.(2023吉林东北师大附中月考)如图,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-.
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求点M的坐标.
类型三 已知图象与x轴的两个交点坐标和另一个点的坐标,通常设交点式
6.(2023山西长治上党期末)在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c过A(-1,0),B(2,0),C(0,-4)三点.
(1)求抛物线的表达式;
(2)P为抛物线第四象限上的一个动点,连结AP交线段BC于点G,如果AG∶GP=3,求点P的坐标.
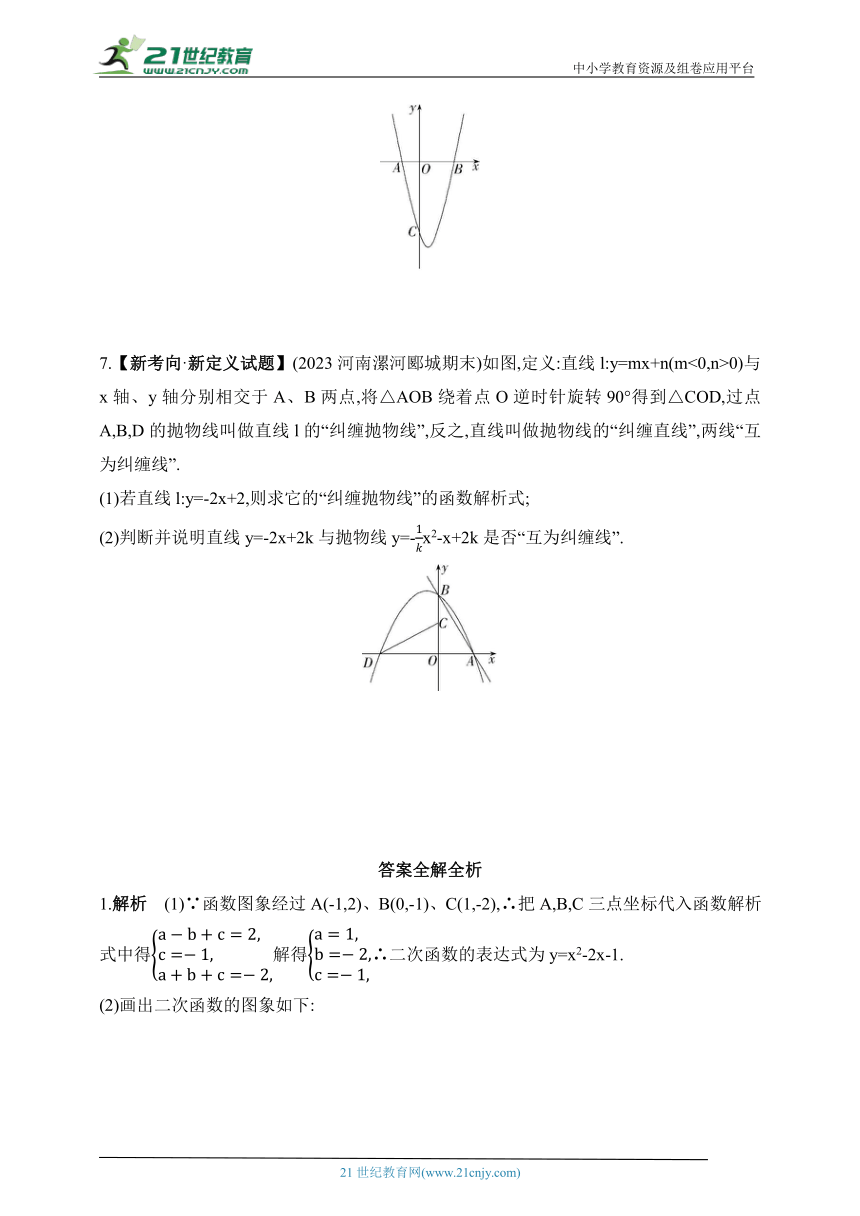
7.【新考向·新定义试题】(2023河南漯河郾城期末)如图,定义:直线l:y=mx+n(m<0,n>0)与x轴、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A,B,D的抛物线叫做直线l的“纠缠抛物线”,反之,直线叫做抛物线的“纠缠直线”,两线“互为纠缠线”.
(1)若直线l:y=-2x+2,则求它的“纠缠抛物线”的函数解析式;
(2)判断并说明直线y=-2x+2k与抛物线y=-x2-x+2k是否“互为纠缠线”.
答案全解全析
1.解析 (1)∵函数图象经过A(-1,2)、B(0,-1)、C(1,-2),∴把A,B,C三点坐标代入函数解析式中得解得∴二次函数的表达式为y=x2-2x-1.
(2)画出二次函数的图象如下:
(3)由图象可知,当02.解析 (1)设二次函数的解析式为y=ax2+bx+c(a≠0),将A、B、C三点坐标代入得解得∴该二次函数的解析式为y=-x2+x+4.
(2)抛物线y=-x2+x+4的对称轴为直线x=-=2,如图,连结AC与对称轴直线x=2交于点D,∵B(0,4),C(4,4),∴B、C关于对称轴直线x=2对称,∴DB=DC,∴AD+BD=AD+CD=AC,∵AB==4,为定值,∴此时△ABD的周长取得最小值,点D即为所求.设直线AC的解析式为y=kx+m(k≠0),将A、C两点坐标代入得解得故直线AC的解析式为y=x+2,当x=2时,y=3,∴当点D的坐标为(2,3)时,△ABD的周长最小.
3.解析 由题意得二次函数的顶点坐标为(5,4),设函数解析式为y=a(x-5)2+4(a≠0),把(2,1)代入得1=9a+4,解得a=-,∴该二次函数的解析式为y=-(x-5)2+4.
4.解析 (1)∵抛物线经过点(-2,3),(0,3),∴抛物线的对称轴为直线x==-1,∵x=1和x=-3所对应的函数值相等,∴m=0.
(2)由(1)可知抛物线的顶点坐标为(-1,4),∴设抛物线解析式为y=a(x+1)2+4(a≠0),把(0,3)代入得3=a×(0+1)2+4,解得a=-1,∴该二次函数的表达式为y=-(x+1)2+4,即y=-x2-2x+3.
5.解析 (1)设抛物线的解析式为y=a+k(a≠0),
把A(2,0)、C(0,3)代入得解得
∴y=-+,即y=-x2-x+3.
(2)由y=0得-+=0,解得x1=2,x2=-3,∴B(-3,0),∴BO=3,如图,分情况求解如下:
①当CM1=BM1时,∵BO=CO=3,∴△BOC是等腰直角三角形,∴当点M1在原点O处时,△MBC是等腰三角形,∴M1(0,0);
②当BC=BM2时,在Rt△BOC中,BO=CO=3,由勾股定理得BC==3,∴BM2=3,∴OM2=BM2-OB=3-3,∴M2(3-3,0);
③当CM3=BC时,易得BM3=6,此时点M3不在线段AB上,∴此情况不符合题意,舍去.
综上所述,当△MBC为等腰三角形时,点M的坐标为(3-3,0)或(0,0).
6.解析 (1)∵抛物线y=ax2+bx+c过点A(-1,0),B(2,0),∴设抛物线的解析式为y=a(x+1)(x-2).将C(0,-4)代入得-2a=-4,解得a=2,∴抛物线的表达式为y=2(x+1)(x-2),即y=2x2-2x-4.
(2)如图,过点P作PE⊥x轴于点E,交BC于点F,过点A作AD⊥x轴交BC的延长线于点D,∴AD∥PE,∴△ADG∽△PFG,∴==3.设直线BC的解析式为y=kx-4(k≠0),将B(2,0)代入得2k-4=0,解得k=2,∴直线BC的解析式为y=2x-4,当x=-1时,y=2x-4=-6,∴AD=6,设P(m,2m2-2m-4),则F(m,2m-4),∴PF=2m-4-(2m2-2m-4)=-2m2+4m,∴==3,整理得m2-2m+1=0,解得m=1,∴P(1,-4).
7.解析 (1)在y=-2x+2中,令y=0,得x=1,令x=0,得y=2,∴A(1,0),B(0,2),∵将△AOB绕着点O逆时针旋转90°得到△COD,∴OD=OB,∴D(-2,0),∵直线y=-2x+2的“纠缠抛物线”过A(1,0),D(-2,0),∴设“纠缠抛物线”的函数解析式为y=a(x+2)(x-1)(a≠0),把B(0,2)代入得2=-2a,∴a=-1,∴直线l:y=-2x+2的“纠缠抛物线”的函数解析式为y=-(x+2)(x-1)=-x2-x+2.
(2)直线y=-2x+2k与抛物线y=-x2-x+2k“互为纠缠线”.
理由如下:在y=-2x+2k中,令x=0,得y=2k,令y=0,得x=k,∴A(k,0),B(0,2k),∵将△AOB绕着点O逆时针旋转90°得到△COD,∴D(-2k,0),∵直线y=-2x+2k的“纠缠抛物线”过A(k,0),
D(-2k,0),∴设“纠缠抛物线”的函数解析式为y=a1(x-k)(x+2k)(a≠0),将B(0,2k)代入得2k=-2k2a1,解得a1=-,∴“纠缠抛物线”的函数解析式为y=-(x-k)(x+2k)=-x2-x+2k,∴直线y=-2x+2k与抛物线y=-x2-x+2k“互为纠缠线”.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学九年级下学期
专项素养综合全练(一)
二次函数表达式的三种常见求解方法
类型一 已知图象上任意三点,通常设一般式
1.(2023江苏徐州铜山期中)如图,已知二次函数y=ax2+bx+c的图象经过点A(-1,2)、B(0,-1)、C(1,-2).
(1)求二次函数的表达式;
(2)画出二次函数的图象;
(3)结合图象,直接写出当0
(1)求该二次函数的解析式;
(2)若在该函数图象的对称轴上有个动点D,求当点D坐标为何值时,△ABD的周长最小.
类型二 已知顶点、对称轴、最值,通常设顶点式
3.(2023吉林长春第二实验中学期中)已知一个二次函数有最大值4,且当x>5时,y随x的增大而减小,当x<5时,y随x的增大而增大,且该函数图象经过点(2,1),求该函数的解析式.
4.(2023河南周口淮阳模拟)已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x … -4 -3 -2 -1 0 1 2 …
y … -5 0 3 4 3 m -5 …
(1)根据表格,直接写出该二次函数的对称轴以及m的值;
(2)求该二次函数的表达式.
5.(2023吉林东北师大附中月考)如图,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-.
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求点M的坐标.
类型三 已知图象与x轴的两个交点坐标和另一个点的坐标,通常设交点式
6.(2023山西长治上党期末)在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c过A(-1,0),B(2,0),C(0,-4)三点.
(1)求抛物线的表达式;
(2)P为抛物线第四象限上的一个动点,连结AP交线段BC于点G,如果AG∶GP=3,求点P的坐标.
7.【新考向·新定义试题】(2023河南漯河郾城期末)如图,定义:直线l:y=mx+n(m<0,n>0)与x轴、y轴分别相交于A、B两点,将△AOB绕着点O逆时针旋转90°得到△COD,过点A,B,D的抛物线叫做直线l的“纠缠抛物线”,反之,直线叫做抛物线的“纠缠直线”,两线“互为纠缠线”.
(1)若直线l:y=-2x+2,则求它的“纠缠抛物线”的函数解析式;
(2)判断并说明直线y=-2x+2k与抛物线y=-x2-x+2k是否“互为纠缠线”.
答案全解全析
1.解析 (1)∵函数图象经过A(-1,2)、B(0,-1)、C(1,-2),∴把A,B,C三点坐标代入函数解析式中得解得∴二次函数的表达式为y=x2-2x-1.
(2)画出二次函数的图象如下:
(3)由图象可知,当0
(2)抛物线y=-x2+x+4的对称轴为直线x=-=2,如图,连结AC与对称轴直线x=2交于点D,∵B(0,4),C(4,4),∴B、C关于对称轴直线x=2对称,∴DB=DC,∴AD+BD=AD+CD=AC,∵AB==4,为定值,∴此时△ABD的周长取得最小值,点D即为所求.设直线AC的解析式为y=kx+m(k≠0),将A、C两点坐标代入得解得故直线AC的解析式为y=x+2,当x=2时,y=3,∴当点D的坐标为(2,3)时,△ABD的周长最小.
3.解析 由题意得二次函数的顶点坐标为(5,4),设函数解析式为y=a(x-5)2+4(a≠0),把(2,1)代入得1=9a+4,解得a=-,∴该二次函数的解析式为y=-(x-5)2+4.
4.解析 (1)∵抛物线经过点(-2,3),(0,3),∴抛物线的对称轴为直线x==-1,∵x=1和x=-3所对应的函数值相等,∴m=0.
(2)由(1)可知抛物线的顶点坐标为(-1,4),∴设抛物线解析式为y=a(x+1)2+4(a≠0),把(0,3)代入得3=a×(0+1)2+4,解得a=-1,∴该二次函数的表达式为y=-(x+1)2+4,即y=-x2-2x+3.
5.解析 (1)设抛物线的解析式为y=a+k(a≠0),
把A(2,0)、C(0,3)代入得解得
∴y=-+,即y=-x2-x+3.
(2)由y=0得-+=0,解得x1=2,x2=-3,∴B(-3,0),∴BO=3,如图,分情况求解如下:
①当CM1=BM1时,∵BO=CO=3,∴△BOC是等腰直角三角形,∴当点M1在原点O处时,△MBC是等腰三角形,∴M1(0,0);
②当BC=BM2时,在Rt△BOC中,BO=CO=3,由勾股定理得BC==3,∴BM2=3,∴OM2=BM2-OB=3-3,∴M2(3-3,0);
③当CM3=BC时,易得BM3=6,此时点M3不在线段AB上,∴此情况不符合题意,舍去.
综上所述,当△MBC为等腰三角形时,点M的坐标为(3-3,0)或(0,0).
6.解析 (1)∵抛物线y=ax2+bx+c过点A(-1,0),B(2,0),∴设抛物线的解析式为y=a(x+1)(x-2).将C(0,-4)代入得-2a=-4,解得a=2,∴抛物线的表达式为y=2(x+1)(x-2),即y=2x2-2x-4.
(2)如图,过点P作PE⊥x轴于点E,交BC于点F,过点A作AD⊥x轴交BC的延长线于点D,∴AD∥PE,∴△ADG∽△PFG,∴==3.设直线BC的解析式为y=kx-4(k≠0),将B(2,0)代入得2k-4=0,解得k=2,∴直线BC的解析式为y=2x-4,当x=-1时,y=2x-4=-6,∴AD=6,设P(m,2m2-2m-4),则F(m,2m-4),∴PF=2m-4-(2m2-2m-4)=-2m2+4m,∴==3,整理得m2-2m+1=0,解得m=1,∴P(1,-4).
7.解析 (1)在y=-2x+2中,令y=0,得x=1,令x=0,得y=2,∴A(1,0),B(0,2),∵将△AOB绕着点O逆时针旋转90°得到△COD,∴OD=OB,∴D(-2,0),∵直线y=-2x+2的“纠缠抛物线”过A(1,0),D(-2,0),∴设“纠缠抛物线”的函数解析式为y=a(x+2)(x-1)(a≠0),把B(0,2)代入得2=-2a,∴a=-1,∴直线l:y=-2x+2的“纠缠抛物线”的函数解析式为y=-(x+2)(x-1)=-x2-x+2.
(2)直线y=-2x+2k与抛物线y=-x2-x+2k“互为纠缠线”.
理由如下:在y=-2x+2k中,令x=0,得y=2k,令y=0,得x=k,∴A(k,0),B(0,2k),∵将△AOB绕着点O逆时针旋转90°得到△COD,∴D(-2k,0),∵直线y=-2x+2k的“纠缠抛物线”过A(k,0),
D(-2k,0),∴设“纠缠抛物线”的函数解析式为y=a1(x-k)(x+2k)(a≠0),将B(0,2k)代入得2k=-2k2a1,解得a1=-,∴“纠缠抛物线”的函数解析式为y=-(x-k)(x+2k)=-x2-x+2k,∴直线y=-2x+2k与抛物线y=-x2-x+2k“互为纠缠线”.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
