人教版九年级上册23.2 中心对称图形导学案
文档属性
| 名称 | 人教版九年级上册23.2 中心对称图形导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 154.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-21 14:21:52 | ||
图片预览

文档简介
《中心对称图形》导学案
年级:八年级 科目:数学 课型:新授课 导师:
班级: 姓名: 小组: 时间:
【学习目标】
1.通过观察图形,能说出中心对称图形的定义,并能准确判断图形是否为中心对称图形。
2.通过动手操作、合作探究,发现并说明中心对称图形的性质,进而能运用这些知识解决相关的简单问题。
3.在学习过程中,通过对中心对称图形的研究,体会类比和转化数学思想的应用,感受中心对称图形的美,体验数学“来源于生活,服务于生活”的奥妙。
【学习重点和难点】
重点:中心对称图形的定义及其性质。
难点:中心对称图形的性质及应用。
【知识链接】
轴对称:在平面内,把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合,那么这个图形就是轴对称图形,这条直线叫做对称轴
旋转: 旋转的三要素:
旋转的性质:对应边 对应角 旋转角
对应点与旋转中心的连线长度
对应点连线的中垂线过
【学法指导】
通过寻找中心对称与轴对称的区别于联系来帮助自己学习。
通过探索中心对称与旋转的关系来加强自己对中心对称的理解。
通过小组讨论,合作学习来提高自己的学习效率。
【课前导学】
下列这些图形绕其中心旋转多少度后与他自身重合?
这些图形的共同特征是都旋转多少度与自身重合?
根据课本提示,我们把这种图形叫做 。
你能用自己的话写出中心对称图形的定义吗?
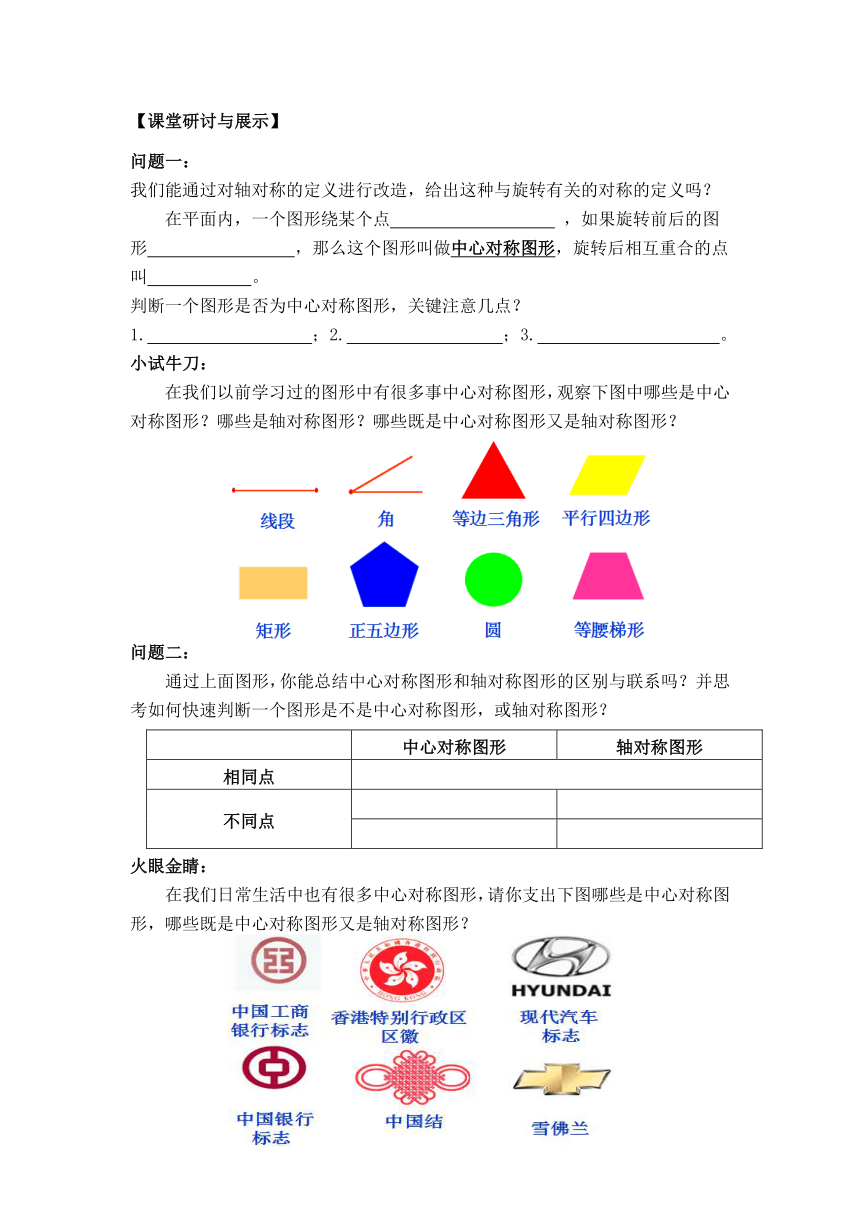
【课堂研讨与展示】
问题一:
我们能通过对轴对称的定义进行改造,给出这种与旋转有关的对称的定义吗?
在平面内,一个图形绕某个点 ,如果旋转前后的图形 ,那么这个图形叫做中心对称图形,旋转后相互重合的点叫 。
判断一个图形是否为中心对称图形,关键注意几点?
1. ;2. ;3. 。
小试牛刀:
在我们以前学习过的图形中有很多事中心对称图形,观察下图中哪些是中心对称图形?哪些是轴对称图形?哪些既是中心对称图形又是轴对称图形?
问题二:
中心对称图形 轴对称图形
相同点
不同点
通过上面图形,你能总结中心对称图形和轴对称图形的区别与联系吗?并思考如何快速判断一个图形是不是中心对称图形,或轴对称图形?
火眼金睛:
在我们日常生活中也有很多中心对称图形,请你支出下图哪些是中心对称图形,哪些既是中心对称图形又是轴对称图形?
问题三:
如图,在□ABCD中;
由平行四边形是中心对称图形,我们可以验证平行四边形的哪些性质?
点A和点C是一对对应点,则OA=OC,同理,OB=OD,那么,在一个中心对称图形中,对称中心平分一对对应点间的连线吗?你发现了什么规律?请把下面的结论补充完整。
结论:中心对称图形的性质:
中心对称图形上的每一对对应点所连成的线段都被对称中心 。
中心对称图形上每一对对应点所连成线段的中点是这个图形的 。
中心对称图形中任意两对对应点的连线交点是这个图形的 。
问题四:
如图,在□ABCD中,过对称中心O的直线EF交AD与点E,交BC与点F。
1.线段OE与OF、AE与CF有怎样的大小关系?
2.被直线EF分成的两个四边形ABFE和四边形CDEF有什么关系?如果旋转直线EF,被直线EF分成的两个图形关系有
变化吗?
3.“过中心对称图形对称中心的任一条直线等分这个图形的周长和面积”这句话对吗?为什么?
奇思妙想:
如图,魔术师老刘有一块儿矩形果园,果园中有一个圆形池塘,老刘想果园连同池塘一次性平均分给两个儿子,但不知怎么分,请你帮帮他?
【知识总结】
说说本节课学习到了哪些方法,哪些思想?
【课堂检测】
在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
2、正多边形中,哪些是中心对称图形?有哪些规律?
······
【课后巩固与练习】
1、下面哪个图形是中心对称图形?
3、EF过□ABCD对角线的交点O,且分别交AB,CD于点E,F,求阴影部分面积与□ABCD的面积的比。
4、*(选作)如图所示有7个完全一样的圆,试画出一条直线将7个圆分成2个部分,使得这2个部分的面积相等。
你能否从上面一题中得到启发想出本题的解决思路?
【小组评价表】
完成情况 知识掌握 动手操作 独立思考 小组合作
较好完成
勉强完成
没有完成
小组长综合评价
年级:八年级 科目:数学 课型:新授课 导师:
班级: 姓名: 小组: 时间:
【学习目标】
1.通过观察图形,能说出中心对称图形的定义,并能准确判断图形是否为中心对称图形。
2.通过动手操作、合作探究,发现并说明中心对称图形的性质,进而能运用这些知识解决相关的简单问题。
3.在学习过程中,通过对中心对称图形的研究,体会类比和转化数学思想的应用,感受中心对称图形的美,体验数学“来源于生活,服务于生活”的奥妙。
【学习重点和难点】
重点:中心对称图形的定义及其性质。
难点:中心对称图形的性质及应用。
【知识链接】
轴对称:在平面内,把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合,那么这个图形就是轴对称图形,这条直线叫做对称轴
旋转: 旋转的三要素:
旋转的性质:对应边 对应角 旋转角
对应点与旋转中心的连线长度
对应点连线的中垂线过
【学法指导】
通过寻找中心对称与轴对称的区别于联系来帮助自己学习。
通过探索中心对称与旋转的关系来加强自己对中心对称的理解。
通过小组讨论,合作学习来提高自己的学习效率。
【课前导学】
下列这些图形绕其中心旋转多少度后与他自身重合?
这些图形的共同特征是都旋转多少度与自身重合?
根据课本提示,我们把这种图形叫做 。
你能用自己的话写出中心对称图形的定义吗?
【课堂研讨与展示】
问题一:
我们能通过对轴对称的定义进行改造,给出这种与旋转有关的对称的定义吗?
在平面内,一个图形绕某个点 ,如果旋转前后的图形 ,那么这个图形叫做中心对称图形,旋转后相互重合的点叫 。
判断一个图形是否为中心对称图形,关键注意几点?
1. ;2. ;3. 。
小试牛刀:
在我们以前学习过的图形中有很多事中心对称图形,观察下图中哪些是中心对称图形?哪些是轴对称图形?哪些既是中心对称图形又是轴对称图形?
问题二:
中心对称图形 轴对称图形
相同点
不同点
通过上面图形,你能总结中心对称图形和轴对称图形的区别与联系吗?并思考如何快速判断一个图形是不是中心对称图形,或轴对称图形?
火眼金睛:
在我们日常生活中也有很多中心对称图形,请你支出下图哪些是中心对称图形,哪些既是中心对称图形又是轴对称图形?
问题三:
如图,在□ABCD中;
由平行四边形是中心对称图形,我们可以验证平行四边形的哪些性质?
点A和点C是一对对应点,则OA=OC,同理,OB=OD,那么,在一个中心对称图形中,对称中心平分一对对应点间的连线吗?你发现了什么规律?请把下面的结论补充完整。
结论:中心对称图形的性质:
中心对称图形上的每一对对应点所连成的线段都被对称中心 。
中心对称图形上每一对对应点所连成线段的中点是这个图形的 。
中心对称图形中任意两对对应点的连线交点是这个图形的 。
问题四:
如图,在□ABCD中,过对称中心O的直线EF交AD与点E,交BC与点F。
1.线段OE与OF、AE与CF有怎样的大小关系?
2.被直线EF分成的两个四边形ABFE和四边形CDEF有什么关系?如果旋转直线EF,被直线EF分成的两个图形关系有
变化吗?
3.“过中心对称图形对称中心的任一条直线等分这个图形的周长和面积”这句话对吗?为什么?
奇思妙想:
如图,魔术师老刘有一块儿矩形果园,果园中有一个圆形池塘,老刘想果园连同池塘一次性平均分给两个儿子,但不知怎么分,请你帮帮他?
【知识总结】
说说本节课学习到了哪些方法,哪些思想?
【课堂检测】
在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
2、正多边形中,哪些是中心对称图形?有哪些规律?
······
【课后巩固与练习】
1、下面哪个图形是中心对称图形?
3、EF过□ABCD对角线的交点O,且分别交AB,CD于点E,F,求阴影部分面积与□ABCD的面积的比。
4、*(选作)如图所示有7个完全一样的圆,试画出一条直线将7个圆分成2个部分,使得这2个部分的面积相等。
你能否从上面一题中得到启发想出本题的解决思路?
【小组评价表】
完成情况 知识掌握 动手操作 独立思考 小组合作
较好完成
勉强完成
没有完成
小组长综合评价
同课章节目录
