数学人教A版(2019)选择性必修第二册4.3.2等比数列的前n项和公式 课件(共14张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.3.2等比数列的前n项和公式 课件(共14张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 16:53:17 | ||
图片预览





文档简介
(共14张PPT)
第 四 章 数 列
4.3.2 等比数列的前n项和公式
延时符
学习目标
理解等比数列的前n项和公式的推导方法,握等比数列的n项和公式并能运用公式解决一些简单问题
提高学生的建模意识,体会公式探求过程中从特殊到一般的思维方法,渗透方程思想、分类讨论思想。
数学抽象、数学运算、数学建模
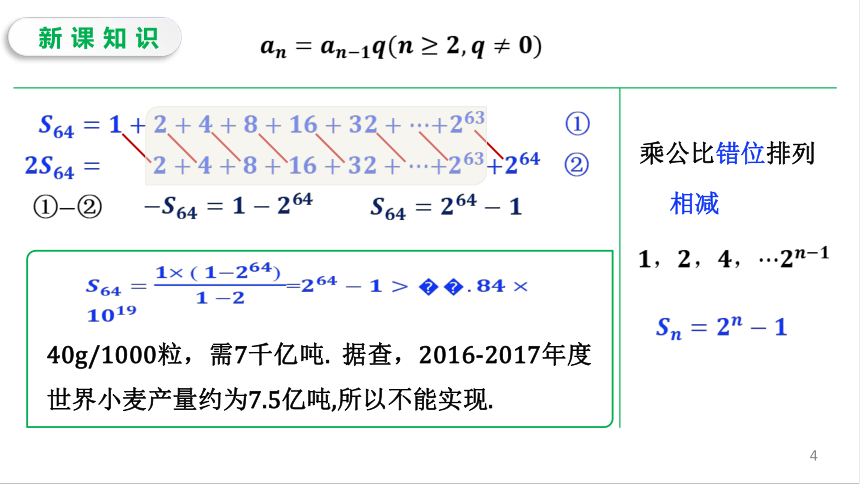
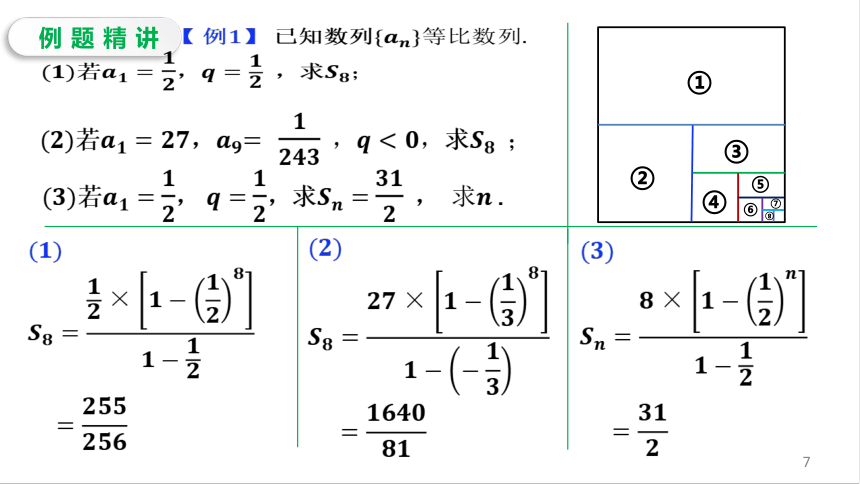
新知导入阅读教材34页回答下面的问题.1.以每个格子的麦粒个数,从小到大排列成为一个数列总共有几项?2.数列是什么数列?通项公式是?3.问题的核心是求等比数列的.前64项和64项等比数列=新课知识=40g/1000粒,需7千亿吨.据查,2016-2017年度世界小麦产量约为7.5亿吨,所以不能实现.①①②②乘公比错位排列相减新课知识①②时时①②等比数列的前n项和公式( * )错位相减新课知识等比数列的前n项和公式当公比不确定时,应当分和两种情况讨论.首项、公比与项数.首项、末项、公比与项数.首项、公比项数错位相减法导出方法:例题精讲【例1】已知数列若,,求①②③④⑤⑥⑦⑧若,=求若,,求,.课堂练习练习1.已知等比数列{an}中,例题精讲【例2】已知等比数列{}的公比≠ -1,前项和为,证明,,成等比数列,并这个数列的公比.【证明】当时==所以成等差数列,公比为.当时因为为常数,,成等比数列.课堂练习课堂练习课堂小结(1)前项和公式的推导:错位相减法;(2)数学思想方法的应用:①方程思想:等比数列求和问题中的“知三求二”问题就是方程思想的重要体现;②分类讨论思想:由等比数列前项和公式可知,解答等比数列求和问题时常常要用到分类讨论思想.当公比不确定时,应当分和两种情况讨论.
本课作业
必做 二
必做 一
必做 三
教材 37 页
练习 3~5
三维 54页
课后 1~8
三维 248页
课后 11,12
01
02
03
微信: 手机:
感谢您的观看
第 四 章 数 列
4.3.2 等比数列的前n项和公式
延时符
学习目标
理解等比数列的前n项和公式的推导方法,握等比数列的n项和公式并能运用公式解决一些简单问题
提高学生的建模意识,体会公式探求过程中从特殊到一般的思维方法,渗透方程思想、分类讨论思想。
数学抽象、数学运算、数学建模
新知导入阅读教材34页回答下面的问题.1.以每个格子的麦粒个数,从小到大排列成为一个数列总共有几项?2.数列是什么数列?通项公式是?3.问题的核心是求等比数列的.前64项和64项等比数列=新课知识=40g/1000粒,需7千亿吨.据查,2016-2017年度世界小麦产量约为7.5亿吨,所以不能实现.①①②②乘公比错位排列相减新课知识①②时时①②等比数列的前n项和公式( * )错位相减新课知识等比数列的前n项和公式当公比不确定时,应当分和两种情况讨论.首项、公比与项数.首项、末项、公比与项数.首项、公比项数错位相减法导出方法:例题精讲【例1】已知数列若,,求①②③④⑤⑥⑦⑧若,=求若,,求,.课堂练习练习1.已知等比数列{an}中,例题精讲【例2】已知等比数列{}的公比≠ -1,前项和为,证明,,成等比数列,并这个数列的公比.【证明】当时==所以成等差数列,公比为.当时因为为常数,,成等比数列.课堂练习课堂练习课堂小结(1)前项和公式的推导:错位相减法;(2)数学思想方法的应用:①方程思想:等比数列求和问题中的“知三求二”问题就是方程思想的重要体现;②分类讨论思想:由等比数列前项和公式可知,解答等比数列求和问题时常常要用到分类讨论思想.当公比不确定时,应当分和两种情况讨论.
本课作业
必做 二
必做 一
必做 三
教材 37 页
练习 3~5
三维 54页
课后 1~8
三维 248页
课后 11,12
01
02
03
微信: 手机:
感谢您的观看
