北师大版九年级上册第六章用树状图与列表法求概率
文档属性
| 名称 | 北师大版九年级上册第六章用树状图与列表法求概率 |  | |
| 格式 | zip | ||
| 文件大小 | 842.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-21 16:03:02 | ||
图片预览









文档简介
课件30张PPT。九年级数学(上)第六章 频率与概率频率与概率的关系:用树状图与列表法求概率九年级数学(上)第六章 频率与概率1、频率与概率的关系:
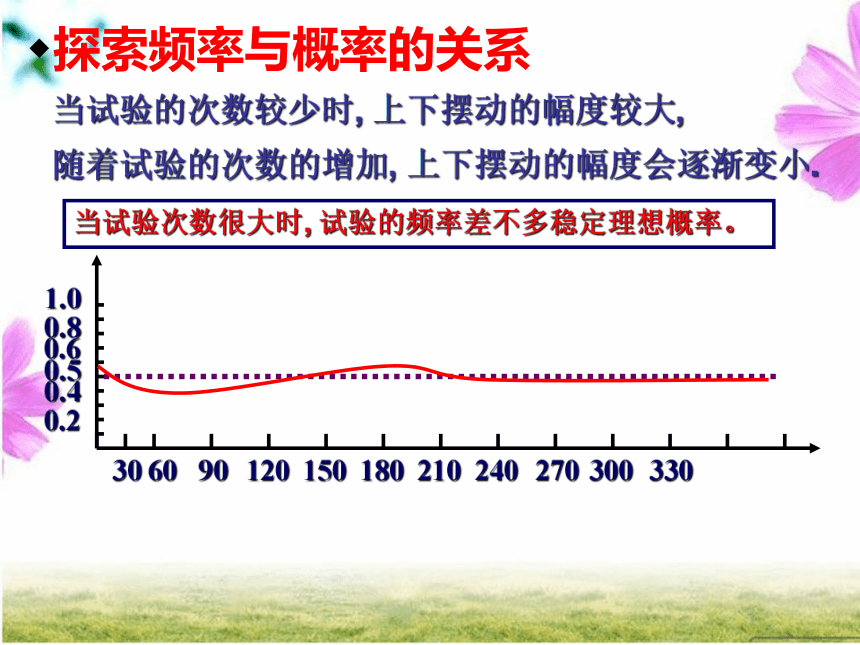
2、用树状图或列表法求概率探索频率与概率的关系做实验:当试验的次数较少时, 上下摆动的幅度较大,随着试验的次数的增加, 上下摆动的幅度会逐渐变小.当试验次数很大时, 试验的频率差不多稳定理想概率。探索频率与概率的关系当试验次数很大时, 试验的频率差不多稳定理想概率。1、频率与概率的关系:因此,我们可以通过多次试验,
用一个事件发生的频率来估计一事件发生的概率.2、用树状图与列表法求概率一步试验,
两步实验.
多步实验:例1 随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少? 共有4种结果,每种结果可能性相同,而至少有一次正面朝上的结果有3种:(正,正),(正,反),(反,正),因此至少有一次正面朝上的概率是3/4.开始正反正反正反(正,正)(正,反)(反,正)(反,反) 请你用列表的方法解答(正,正)
(正,反)
(反,正)
(反,反)
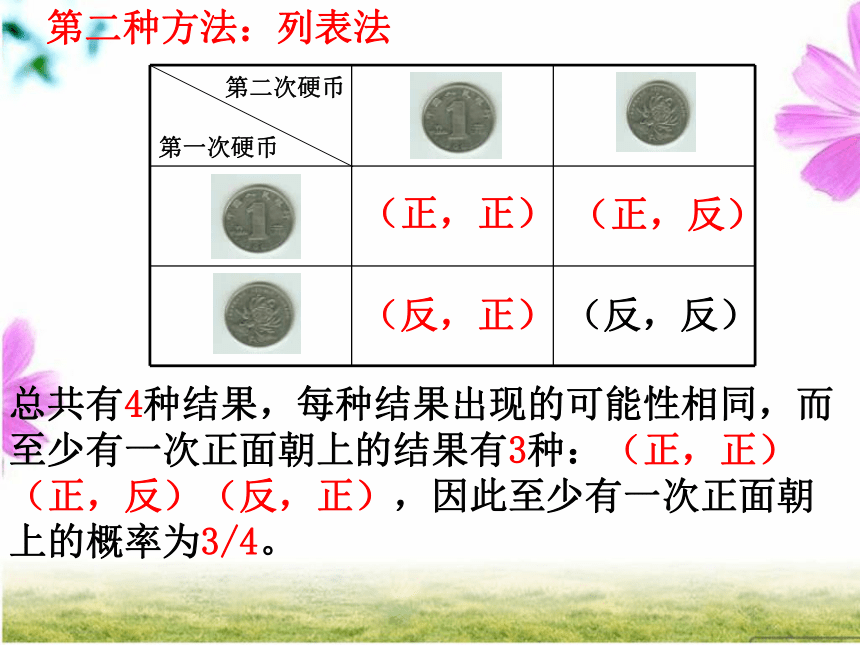
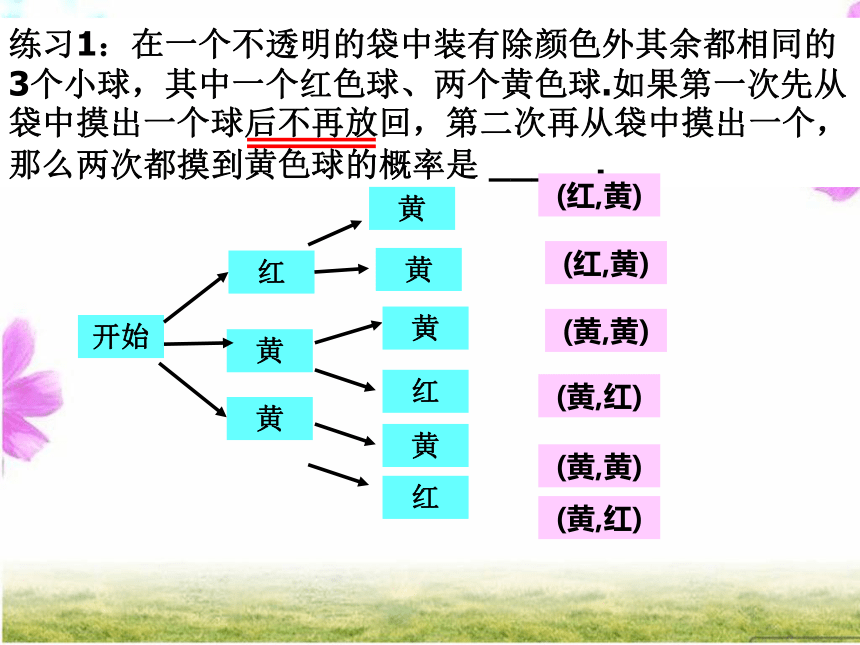
第二种方法:列表法总共有4种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有3种:(正,正)(正,反)(反,正),因此至少有一次正面朝上的概率为3/4。求概率时,各种情况出现的可能性必须相同。求概率时应注意些什么? 练习1:在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.开始红黄黄(红,黄)黄黄红黄红(黄,黄)(黄,红)(黄,黄)(黄,红)黄(红,黄)(2)在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后再放回摇匀,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.猜一猜.小明和弟弟在玩猜点数的游戏,规则是这样的:将红桃A至红桃5、黑桃A至黑桃5两组扑克牌分别洗匀,每次从两种花色中各抽出一张,抽后并放回洗匀,在抽之前猜一个数,如果每次抽出的两张牌的点数之和与猜的数相同算对,否则算错,谁猜对的多算赢。小明每次说的数不是4就是5;弟弟每次说的数不是6就是7,那么谁赢的可能大呢?若你来猜会猜哪两个数呢?为什么?带你进入尖子生行列(3)有两组扑克牌,第一组是1和2,第二组是1、2和 3,从两组中各抽一张,和等于4的概率是_____;和不小于3的概率是______.解:所有可能出现的结果为黑A黑2黑3黑4黑5黑A黑2黑3黑4黑5黑A黑2黑3黑4黑5黑A黑2黑3黑4黑5黑A黑2黑3黑4黑5两张牌面数字和的所有结果为2,3,4,5,6,3,4,5,6,7,……. 猜一猜用表格表示概率黑桃红桃牌面数字和
所有可能结果 因为牌面数字和为6的概率最大,所以弟弟赢的可能性大。 猜一猜用表格表示概率一.将一个均匀的硬币上抛三次,结果为三个正面的概率为______________.解:开始反正正反反正正反反反正反正正第一次:第二次:第三次:总共有8种结果,每种结果出现的可能性相同,而三次正面朝上的结果有1种,因此三次正面朝上的概率为1/8。1/8 掷两枚骰子,它们的点数和可能有哪些值?
用列表的方法求:(1)“点数和为7点”的概率;
(2)“两颗骰子点数相同”的概率;(3)两颗骰子点数都是相同偶数的概率。(1,6)
(2,5)(3,4)(4,3)(5,2)(6,1)(1,1)(2,2)(3,3)(4,4)(5,5)(6,6)二.1.一个家庭有两个孩子,从出生的先后顺序和性别上来分,所有可能出现的情况( )
(A)男女 ,男男,女男 (B)男女 ,女男
(C)男女 ,男男,女男,女女, (D)男男,女女C 随堂练习2.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少? 随堂练习2.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?解:设两双袜子分别为A1、A2、B1、B2,则所以穿相同一双袜子的概率为第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2(A1,A2)(A1,B1)(A1,B2)(A2,A1)(A2,B1)(A2,B2)(B1,A1)(B1,A2)(B1,B2)(B2,A1)(B2,A2)(B2,B1)用表格求所有可能结果时,你可要特别谨慎哦
3.有长度分别为2cm,2cm,4cm,5cm的小棒各一根,放在不透明的纸盒中,每次从中任意取一根小棒(不放回),取了三次,取得的三根小棒恰好能构成一个三角形的概率是多少? 随堂练习5、 两个转盘都被分成黑白相等的两部分,甲乙两人用它们做游戏,如果两个指针所停区域的颜色不同,则乙获胜,在这个游戏中( )
(A)甲获胜的可能性大
(B)乙获胜的可能性大
(C)两人获胜的可能性一样大
(D)不能确定谁获胜的可能性大C 随堂练习试一试:一个家庭有三个孩子,若一个孩子是男孩还是女孩的可能性相同.
(1)求这个家庭的3个孩子都是男孩的概率;(2)求这个家庭有2个男孩和1个女孩的概率;(3)求这个家庭至少有一个男孩的概率.解:(1)这个家庭的3个孩子都是男孩的概率为1/8;(2)这个家庭有2个男孩和1个女孩的概率为3/8;(3)这个家庭至少有一个男孩的概率为7/8. 归纳总结,画龙点睛1、本节课你有哪些收获?有何感想?
2、用列表法求概率时应注意什么情况?用列表法求随机事件发生的理论概率
(也可借用树状图分析)学会了明白了用列表法求概率时应注意各种情况发生的可
能性务必相同懂得了合作交流的重要性利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.结束寄语询问者智之本,思虑者智之道也.结束寄语统计的基本思想:
用样本去估计总体.
用频率去估计概率.作业:1,练习册70-71页:
2,第四章考试卷。
认真独立完成,检验本章的学习效果。
2、用树状图或列表法求概率探索频率与概率的关系做实验:当试验的次数较少时, 上下摆动的幅度较大,随着试验的次数的增加, 上下摆动的幅度会逐渐变小.当试验次数很大时, 试验的频率差不多稳定理想概率。探索频率与概率的关系当试验次数很大时, 试验的频率差不多稳定理想概率。1、频率与概率的关系:因此,我们可以通过多次试验,
用一个事件发生的频率来估计一事件发生的概率.2、用树状图与列表法求概率一步试验,
两步实验.
多步实验:例1 随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少? 共有4种结果,每种结果可能性相同,而至少有一次正面朝上的结果有3种:(正,正),(正,反),(反,正),因此至少有一次正面朝上的概率是3/4.开始正反正反正反(正,正)(正,反)(反,正)(反,反) 请你用列表的方法解答(正,正)
(正,反)
(反,正)
(反,反)
第二种方法:列表法总共有4种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有3种:(正,正)(正,反)(反,正),因此至少有一次正面朝上的概率为3/4。求概率时,各种情况出现的可能性必须相同。求概率时应注意些什么? 练习1:在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.开始红黄黄(红,黄)黄黄红黄红(黄,黄)(黄,红)(黄,黄)(黄,红)黄(红,黄)(2)在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后再放回摇匀,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.猜一猜.小明和弟弟在玩猜点数的游戏,规则是这样的:将红桃A至红桃5、黑桃A至黑桃5两组扑克牌分别洗匀,每次从两种花色中各抽出一张,抽后并放回洗匀,在抽之前猜一个数,如果每次抽出的两张牌的点数之和与猜的数相同算对,否则算错,谁猜对的多算赢。小明每次说的数不是4就是5;弟弟每次说的数不是6就是7,那么谁赢的可能大呢?若你来猜会猜哪两个数呢?为什么?带你进入尖子生行列(3)有两组扑克牌,第一组是1和2,第二组是1、2和 3,从两组中各抽一张,和等于4的概率是_____;和不小于3的概率是______.解:所有可能出现的结果为黑A黑2黑3黑4黑5黑A黑2黑3黑4黑5黑A黑2黑3黑4黑5黑A黑2黑3黑4黑5黑A黑2黑3黑4黑5两张牌面数字和的所有结果为2,3,4,5,6,3,4,5,6,7,……. 猜一猜用表格表示概率黑桃红桃牌面数字和
所有可能结果 因为牌面数字和为6的概率最大,所以弟弟赢的可能性大。 猜一猜用表格表示概率一.将一个均匀的硬币上抛三次,结果为三个正面的概率为______________.解:开始反正正反反正正反反反正反正正第一次:第二次:第三次:总共有8种结果,每种结果出现的可能性相同,而三次正面朝上的结果有1种,因此三次正面朝上的概率为1/8。1/8 掷两枚骰子,它们的点数和可能有哪些值?
用列表的方法求:(1)“点数和为7点”的概率;
(2)“两颗骰子点数相同”的概率;(3)两颗骰子点数都是相同偶数的概率。(1,6)
(2,5)(3,4)(4,3)(5,2)(6,1)(1,1)(2,2)(3,3)(4,4)(5,5)(6,6)二.1.一个家庭有两个孩子,从出生的先后顺序和性别上来分,所有可能出现的情况( )
(A)男女 ,男男,女男 (B)男女 ,女男
(C)男女 ,男男,女男,女女, (D)男男,女女C 随堂练习2.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少? 随堂练习2.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?解:设两双袜子分别为A1、A2、B1、B2,则所以穿相同一双袜子的概率为第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2(A1,A2)(A1,B1)(A1,B2)(A2,A1)(A2,B1)(A2,B2)(B1,A1)(B1,A2)(B1,B2)(B2,A1)(B2,A2)(B2,B1)用表格求所有可能结果时,你可要特别谨慎哦
3.有长度分别为2cm,2cm,4cm,5cm的小棒各一根,放在不透明的纸盒中,每次从中任意取一根小棒(不放回),取了三次,取得的三根小棒恰好能构成一个三角形的概率是多少? 随堂练习5、 两个转盘都被分成黑白相等的两部分,甲乙两人用它们做游戏,如果两个指针所停区域的颜色不同,则乙获胜,在这个游戏中( )
(A)甲获胜的可能性大
(B)乙获胜的可能性大
(C)两人获胜的可能性一样大
(D)不能确定谁获胜的可能性大C 随堂练习试一试:一个家庭有三个孩子,若一个孩子是男孩还是女孩的可能性相同.
(1)求这个家庭的3个孩子都是男孩的概率;(2)求这个家庭有2个男孩和1个女孩的概率;(3)求这个家庭至少有一个男孩的概率.解:(1)这个家庭的3个孩子都是男孩的概率为1/8;(2)这个家庭有2个男孩和1个女孩的概率为3/8;(3)这个家庭至少有一个男孩的概率为7/8. 归纳总结,画龙点睛1、本节课你有哪些收获?有何感想?
2、用列表法求概率时应注意什么情况?用列表法求随机事件发生的理论概率
(也可借用树状图分析)学会了明白了用列表法求概率时应注意各种情况发生的可
能性务必相同懂得了合作交流的重要性利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.结束寄语询问者智之本,思虑者智之道也.结束寄语统计的基本思想:
用样本去估计总体.
用频率去估计概率.作业:1,练习册70-71页:
2,第四章考试卷。
认真独立完成,检验本章的学习效果。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
