25.7相似多边形和图形的位似分层练习(含答案)
文档属性
| 名称 | 25.7相似多边形和图形的位似分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 773.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
25.7相似多边形和图形的位似
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题不正确的是( )
A.两个位似图形一定相似
B.位似图形的对应边若不在同一直线上,那么一定平行
C.两个位似图形的位似比就是相似比
D.两个相似图形一定是位似图形
2.如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若OB=3OB',则△A'B'C'的面积与△ABC的面积之比是( )
A.1:3 B.2:3 C.1:6 D.1:9
3.如图,把菱形沿着对角线的方向移动到菱形的位置,它们的重叠部分(图中阴影部分)的面积是菱形的面积的.若,菱形移动的距离是( )
A. B. C. D.
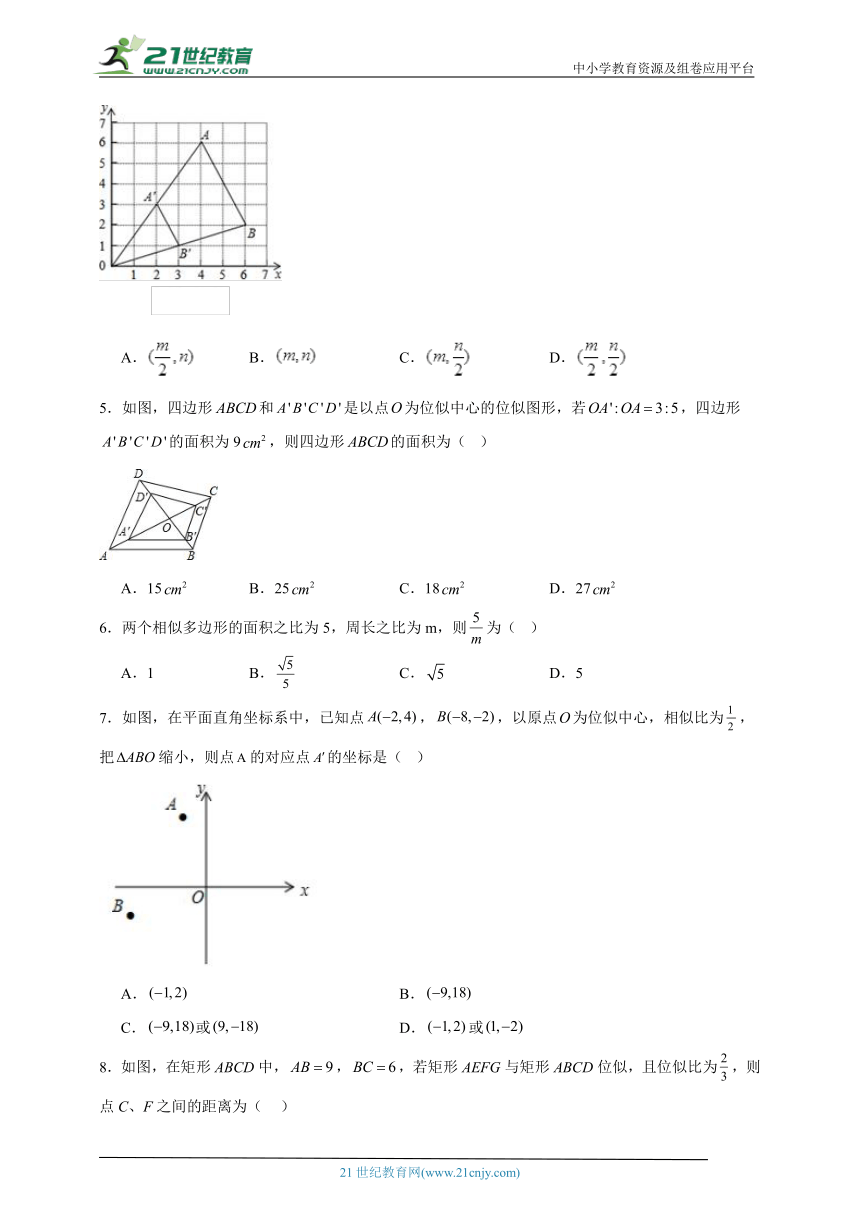
4.如图,△ABO缩小后变为,其中A、B的对应点分别为,均在图中格点上,若线段AB上有一点,则点在上的对应点的坐标为( ).
A. B. C. D.
5.如图,四边形和是以点为位似中心的位似图形,若,四边形的面积为9,则四边形的面积为( )
A.15 B.25 C.18 D.27
6.两个相似多边形的面积之比为5,周长之比为m,则为( )
A.1 B. C. D.5
7.如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )
A. B.
C.或 D.或
8.如图,在矩形ABCD中,,,若矩形AEFG与矩形ABCD位似,且位似比为,则点C、F之间的距离为( )
A.2 B.3 C. D.
9.如图,在矩形中,点分别在上,四边形是正方形,矩形矩形,则的值为( )
A. B. C. D.
10.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,将EFO放大为原来的2倍,则点E的对应点E1的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
二、填空题
11.在平面直角坐标系中,△ABC和△A1B1C1是以坐标原点O为位似中心的位似图形,且位似比等于,若点A的坐标为(3,6),则其对应点A1的坐标是 .
12.五边形位似于五边形,它们的面积比为,已知位似中心到点的距离为,那么到的距离为
13.如图,△OAB和△OCD位似,位似中心是原点O,B点坐标是(6,2),△OAB和△OCD的相似比为2:1,则点D的坐标为 .
14.如图所示,一般书本的纸张是原纸张多次对开得到,矩形沿对开后,再把矩形沿对开,依次类推,若各种开本的矩形都相似,那么的值为 .
15.位似图形的性质
(1)位似图形是相似图形的特例,位似图形不仅相似,而且对应顶点的连线相交于 .
(2)位似图形 相似图形,但相似图形 位似图形,位似图形具有相似图形的所有性质.
(3)位似图形的对应边互相平行或 .
(4)位似图形上任意一对对应点到位似中心的距离之比等于 .
16.宽与长的比等于黄金比的矩形称为黄金矩形.古希腊很多矩形建筑中宽与长的比都等于黄金比,如图,矩形ABCD为黄金矩形,AB<AD,以AB为边在矩形ABCD内部作正方形ABEF,若AD=1,则DF= .
17.如图,点A(3,4),点B(4,0),以O为位似中心,按比例1∶2,将△AOB放大后得△A1O1B1,则A1坐标为 .
18.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的横坐标是a,则点B的对应点B′的横坐标是 .
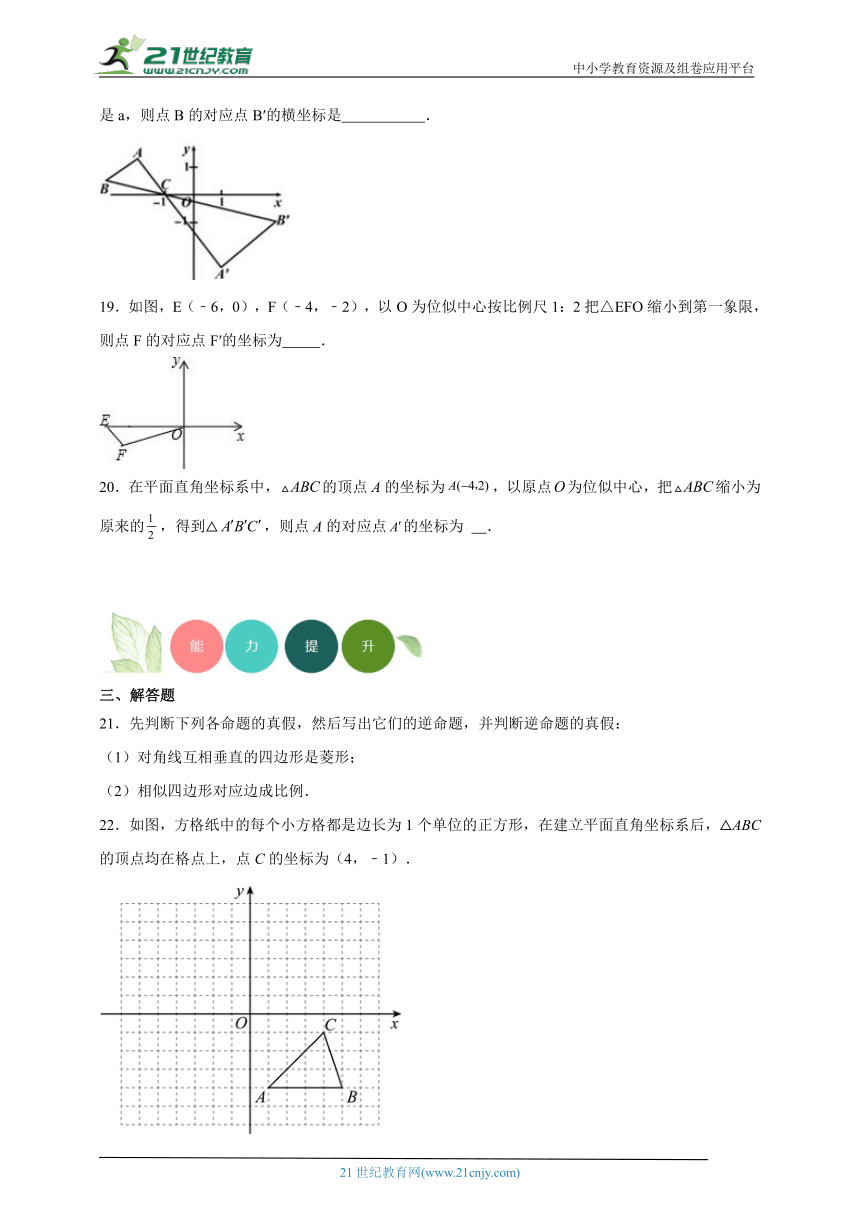
19.如图,E(﹣6,0),F(﹣4,﹣2),以O为位似中心按比例尺1:2把△EFO缩小到第一象限,则点F的对应点F′的坐标为 .
20.在平面直角坐标系中,的顶点A的坐标为,以原点为位似中心,把缩小为原来的,得到△,则点A的对应点的坐标为 .
三、解答题
21.先判断下列各命题的真假,然后写出它们的逆命题,并判断逆命题的真假:
(1)对角线互相垂直的四边形是菱形;
(2)相似四边形对应边成比例.
22.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
(1)写出A、B的坐标;
(2)在网格图中,画出△ABC以点B为位似中心,放大到2倍后的位似△A1BC1,并求出△A1BC1的面积.
23.已知△ABC和△A′B′C′的顶点坐标如下表:
(1)将下表补充完整,并在下面的坐标系中,画出△A′B′C′;
( , )
( , )
(2)观察△ABC与△A′B′C′,写出有关这两个三角形关系的一个正确结论.
24.已知三个顶点的坐标分别为,
(1)将向左平移4个单位长度,再向上平移1个单位长度,得到,请在网格中画出;
(2)以点O为位似中心,在第一象限画出,使它与的相似比为2,并写出点的坐标.
25.在平面直角坐标系中,已知线段与线段关于原点O中心对称,点是点A的对应点,点是点的对应点.
(1)画出线段和;
(2)画出线段以点O为位似中心,位似比为的线段,并直接写出的值.
参考答案:
1.D
2.D
3.D
4.D
5.B
6.C
7.D
8.D
9.A
10.C
11.(9,18)或(-9,-18)/(-9,-18)或(9,18)
12.9
13.(3,1)
14.
15. 一点 是 不一定是 共线 相似比
16.
17.或
18.-2a-3
19.(2,1).
20.(﹣2,1)或(2,﹣1).
21.(1)原命题是假命题;逆命题:菱形的对角线互相垂直;逆命题是真命题;(2)原命题是真命题;逆命题:四条边分别对应成比例的四边形是相似四边形;逆命题是假命题.
22.(1)A(1,﹣4)B(5,﹣4);(2)面积为24.
23.(1)略;(2)相似
24.(1)略
(2)点的坐标为
25.(1)略
(2)=1或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
25.7相似多边形和图形的位似
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题不正确的是( )
A.两个位似图形一定相似
B.位似图形的对应边若不在同一直线上,那么一定平行
C.两个位似图形的位似比就是相似比
D.两个相似图形一定是位似图形
2.如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若OB=3OB',则△A'B'C'的面积与△ABC的面积之比是( )
A.1:3 B.2:3 C.1:6 D.1:9
3.如图,把菱形沿着对角线的方向移动到菱形的位置,它们的重叠部分(图中阴影部分)的面积是菱形的面积的.若,菱形移动的距离是( )
A. B. C. D.
4.如图,△ABO缩小后变为,其中A、B的对应点分别为,均在图中格点上,若线段AB上有一点,则点在上的对应点的坐标为( ).
A. B. C. D.
5.如图,四边形和是以点为位似中心的位似图形,若,四边形的面积为9,则四边形的面积为( )
A.15 B.25 C.18 D.27
6.两个相似多边形的面积之比为5,周长之比为m,则为( )
A.1 B. C. D.5
7.如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )
A. B.
C.或 D.或
8.如图,在矩形ABCD中,,,若矩形AEFG与矩形ABCD位似,且位似比为,则点C、F之间的距离为( )
A.2 B.3 C. D.
9.如图,在矩形中,点分别在上,四边形是正方形,矩形矩形,则的值为( )
A. B. C. D.
10.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,将EFO放大为原来的2倍,则点E的对应点E1的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
二、填空题
11.在平面直角坐标系中,△ABC和△A1B1C1是以坐标原点O为位似中心的位似图形,且位似比等于,若点A的坐标为(3,6),则其对应点A1的坐标是 .
12.五边形位似于五边形,它们的面积比为,已知位似中心到点的距离为,那么到的距离为
13.如图,△OAB和△OCD位似,位似中心是原点O,B点坐标是(6,2),△OAB和△OCD的相似比为2:1,则点D的坐标为 .
14.如图所示,一般书本的纸张是原纸张多次对开得到,矩形沿对开后,再把矩形沿对开,依次类推,若各种开本的矩形都相似,那么的值为 .
15.位似图形的性质
(1)位似图形是相似图形的特例,位似图形不仅相似,而且对应顶点的连线相交于 .
(2)位似图形 相似图形,但相似图形 位似图形,位似图形具有相似图形的所有性质.
(3)位似图形的对应边互相平行或 .
(4)位似图形上任意一对对应点到位似中心的距离之比等于 .
16.宽与长的比等于黄金比的矩形称为黄金矩形.古希腊很多矩形建筑中宽与长的比都等于黄金比,如图,矩形ABCD为黄金矩形,AB<AD,以AB为边在矩形ABCD内部作正方形ABEF,若AD=1,则DF= .
17.如图,点A(3,4),点B(4,0),以O为位似中心,按比例1∶2,将△AOB放大后得△A1O1B1,则A1坐标为 .
18.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的横坐标是a,则点B的对应点B′的横坐标是 .
19.如图,E(﹣6,0),F(﹣4,﹣2),以O为位似中心按比例尺1:2把△EFO缩小到第一象限,则点F的对应点F′的坐标为 .
20.在平面直角坐标系中,的顶点A的坐标为,以原点为位似中心,把缩小为原来的,得到△,则点A的对应点的坐标为 .
三、解答题
21.先判断下列各命题的真假,然后写出它们的逆命题,并判断逆命题的真假:
(1)对角线互相垂直的四边形是菱形;
(2)相似四边形对应边成比例.
22.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
(1)写出A、B的坐标;
(2)在网格图中,画出△ABC以点B为位似中心,放大到2倍后的位似△A1BC1,并求出△A1BC1的面积.
23.已知△ABC和△A′B′C′的顶点坐标如下表:
(1)将下表补充完整,并在下面的坐标系中,画出△A′B′C′;
( , )
( , )
(2)观察△ABC与△A′B′C′,写出有关这两个三角形关系的一个正确结论.
24.已知三个顶点的坐标分别为,
(1)将向左平移4个单位长度,再向上平移1个单位长度,得到,请在网格中画出;
(2)以点O为位似中心,在第一象限画出,使它与的相似比为2,并写出点的坐标.
25.在平面直角坐标系中,已知线段与线段关于原点O中心对称,点是点A的对应点,点是点的对应点.
(1)画出线段和;
(2)画出线段以点O为位似中心,位似比为的线段,并直接写出的值.
参考答案:
1.D
2.D
3.D
4.D
5.B
6.C
7.D
8.D
9.A
10.C
11.(9,18)或(-9,-18)/(-9,-18)或(9,18)
12.9
13.(3,1)
14.
15. 一点 是 不一定是 共线 相似比
16.
17.或
18.-2a-3
19.(2,1).
20.(﹣2,1)或(2,﹣1).
21.(1)原命题是假命题;逆命题:菱形的对角线互相垂直;逆命题是真命题;(2)原命题是真命题;逆命题:四条边分别对应成比例的四边形是相似四边形;逆命题是假命题.
22.(1)A(1,﹣4)B(5,﹣4);(2)面积为24.
23.(1)略;(2)相似
24.(1)略
(2)点的坐标为
25.(1)略
(2)=1或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
