第三章 直线与圆的位置关系课件

课件34张PPT。 九年级数学(下)第三章 圆
5.直线和圆的位置关系(1)
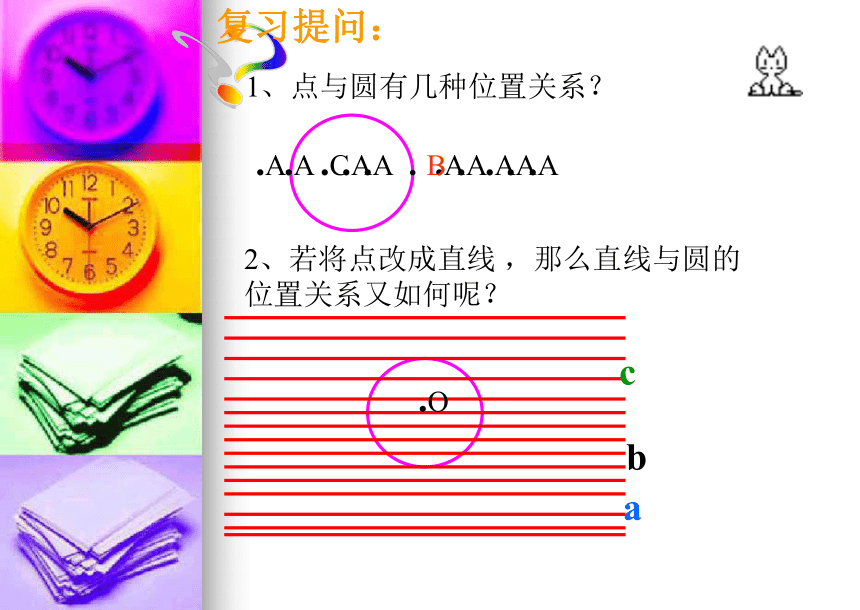
切线及切线性质定理1、点与圆有几种位置关系？？复习提问：2、若将点改成直线 ，那么直线与圆的
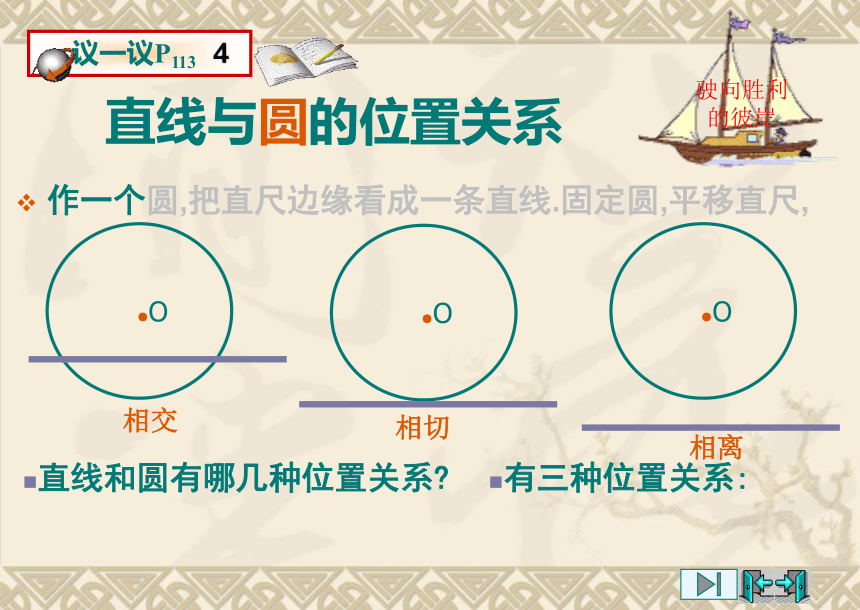
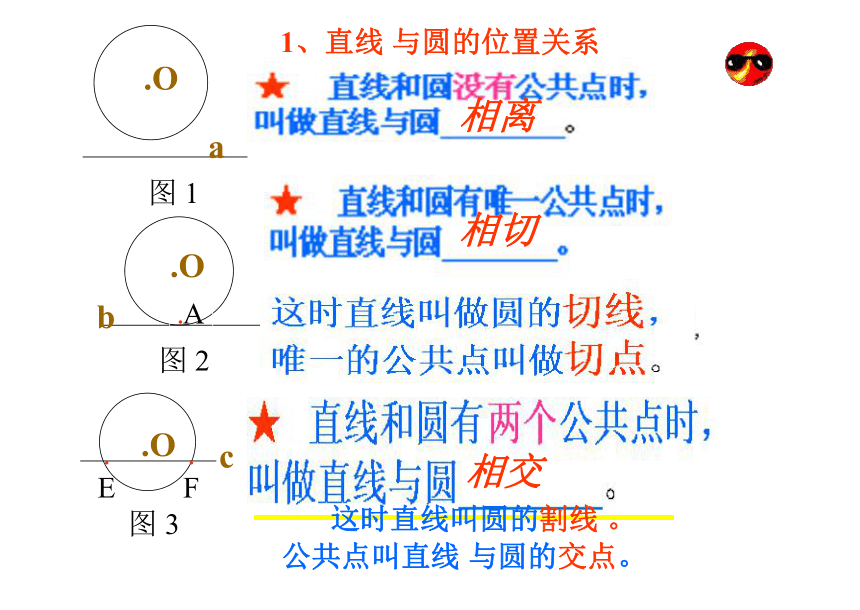
位置关系又如何呢？.A.A.A.A.A . B.A.A.C.A.A.Oabc直线与圆的位置关系1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?你发现这个自然现象反映出直线和圆的位置关系有哪几种?驶向胜利的彼岸a(地平线)a(地平线)直线与圆的位置关系2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的?你发现这个自然现象反映出直线和圆的位置关系有哪几种?驶向胜利的彼岸a(地平线)a(地平线)驶向胜利的彼岸直线与圆的位置关系作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,直线和圆有哪几种位置关系?有三种位置关系:相交相切相离1、直线 与圆的位置关系图 1b.A.O图 2c.
F.E.O图 3相离相切相交 这时直线叫圆的割线 。
公共点叫直线 与圆的交点。小结： 直线与圆有_____种位置关系，是
用直线与圆的________的个数来定义
的。这也是判断直线 与圆的位置关系
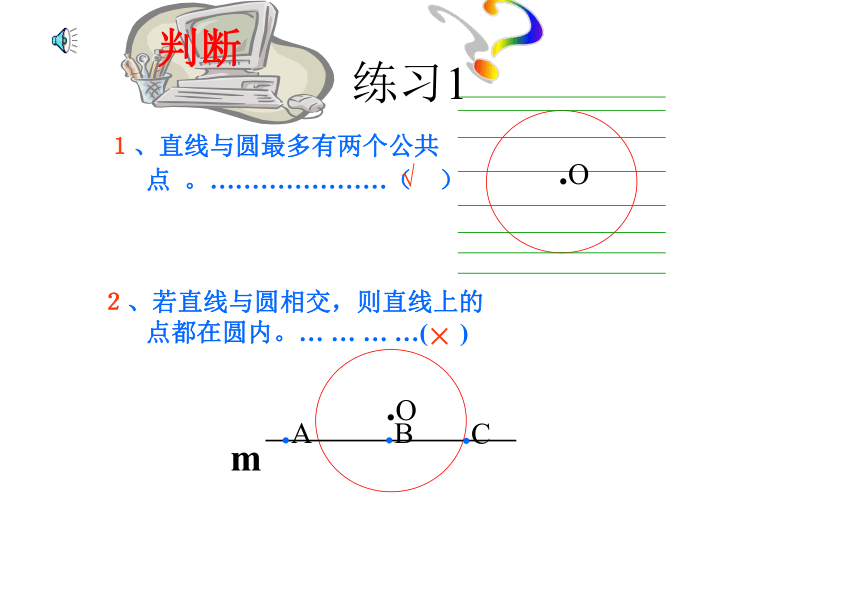
的重要方法.三公共点练习1 １、直线与圆最多有两个公共
点 。…………………（　）
２、若直线与圆相交，则直线上的
点都在圆内。… … … …( )
√×？判断.A.B.C.O.Om3 、若A、B是⊙O外两点， 则直线AB
与⊙O相离。… … … … …( )
4 、若C为⊙O内与O点不重合的一点，
则直线CO与⊙O相交。（ ）
√×.A.B.C.O想一想？若C为⊙O内的一点，A为任意一点，
则直线AC与⊙O一定相交。是否正确？.O.C复习提问：？3、如何根据圆心到点的距离d与半径r的
关系判别点与圆的位置关系？1、什么叫点到直线的距离？2、连结直线外一点与直线上所有点
的线段中,最短的是______？ 直线外一点到这条直线
垂线段的长度叫点到直线 的距离。垂线段1、点到圆心的距离___于半径时，点在圆外。
2、点到圆心的距离___于半径时，点在圆上。
3、点到圆心的距离___于半径时，点在圆内。.E.
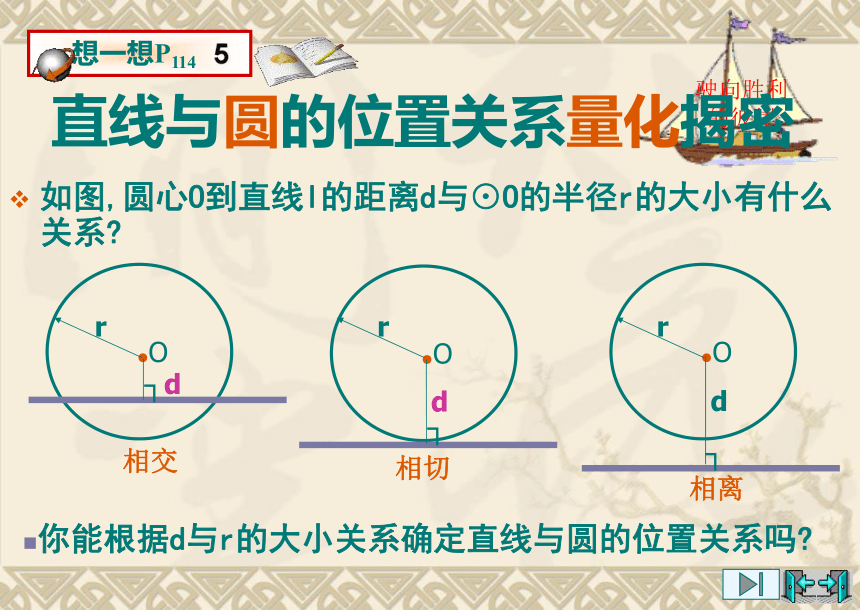
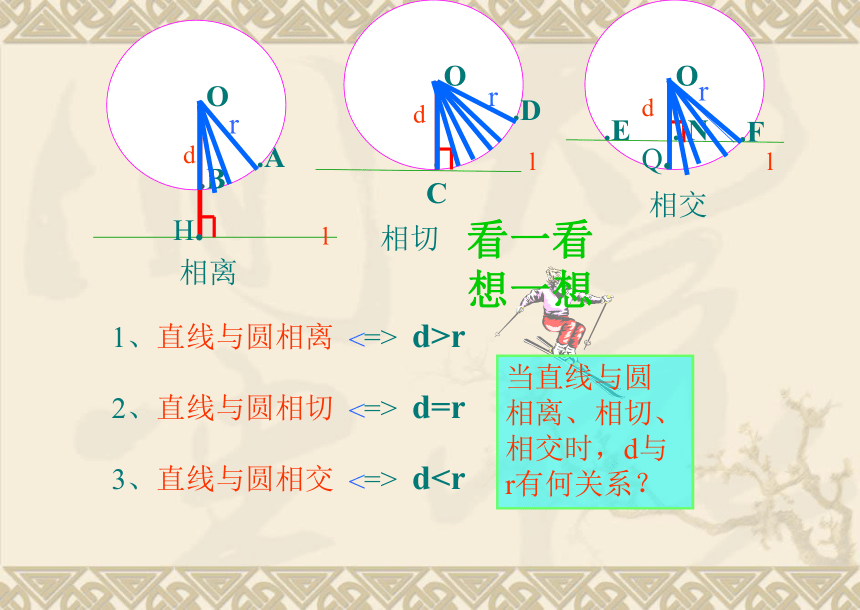
Da如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系? 驶向胜利的彼岸你能根据d与r的大小关系确定直线与圆的位置关系吗?直线与圆的位置关系量化揭密ddd.O.O.Orrr相离相切相交1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d<
<
看一看想一想当直线与圆
相离、相切、
相交时，d与
r有何关系？lll.A.B.
C.D.E.F. NH.Q.讲解符号“< => ”读作___________，它表示两个方面：（1）“＝＞”即从____端可以推出___端
（反映直线与圆的某种位置关系的性质。）；（2）“＜＝”即从____端可以推出___端
（反映直线与圆的某种位置关系的判定。）。等价于左右右左3、直线与圆相交 < => d d>r2、直线与圆相切 < => d=r直线与圆的位置关系dr 2交点割线1切点切线0总结：判定直线 与圆的位置关系的方法有____种：（1）根据定义，由________________
的个数来判断；（2）根据性质，由_______________________________的关系来判断。在实际应用中，常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r练习2填空：1、已知⊙O的半径为5cm，O到
直线a的距离为3cm，则⊙O与直
线a的位置关系是_____。直线a
与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm，
O到直线a的距离是4cm，
则⊙O与直线a的位置关系是 ___ _。动动脑筋相交 相切两个
3、已知⊙O的半径为6cm，O到
直线a的距离为7cm，则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm，
O到直线a的距离是4cm，
则⊙O与直线a的位置关系是 ___ _。零相离思考：圆心A到X轴、
Y轴的距离各是多少?例题1：.AO已知⊙A的直径为6，点A的坐标为
（-3，-4），则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切例题2： 讲解在Rt△ABC中，∠C=90°，AC=3cm，
BC=4cm，以C为圆心，r为半径的圆
与AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm (3)r=3cm。BCA分析：要了解AB与⊙C的位置
关系，只要知道圆心C到AB的
距离d与r的关系。解：过C作CD⊥AB，垂足为D。在Rt△ABC中，AB= ==5（cm）根据三角形面积公式有CD·AB=AC·BC∴CD= ==2.4（cm）。2222D4532.4cm即圆心C到AB的距离d=2.4cm。（1）当r=2cm时， ∵d＞r，
∴⊙C与AB相离。（2）当r=2.4cm时，∵d=r，
∴⊙C与AB相切。（3）当r=3cm时， ∵d＜r，
∴⊙C与AB相交。ABCAD453d=2.4cm解：过C作CD⊥AB，垂足为D。在Rt△ABC中，AB= ==5（cm）根据三角形面积公式有CD·AB=AC·BC∴CD= ==2.4（cm）。2222在Rt△ABC中，∠C=90°，
AC=3cm，BC=4cm，
以C为圆心，r为半径的圆
与AB有怎样的位置关系？
为什么？（1）r=2cm；
（2）r=2.4cm (3)r=3cm。讨论在Rt△ABC中，∠C=90°，AC=3cm，
BC=4cm，以C为圆心，r为半径作圆。1、当r满足________________时，
⊙C与直线AB相离。2、当r满足____________ 时，
⊙C与直线AB相切。3、当r满足____________时，
⊙C与直线AB相交。BCAD45d=2.4cm30cmAC=3cm，BC=4cm，
以C为圆心，r为半径作圆。想一想? 当r满足___________
_____________时,⊙C与线
段AB只有一个公共点. r=2.4cm或 3cm若⊙O与直线a至多只有一个公共点，则d与r的
关系是……………………（ ）
A、d≤r B、d＜r C、d≥r D、d＝r2、设⊙O的半径为r，直线a上一点到圆心的
距离为d，若d=r，则直线a与⊙O的位置关系
是……………………………………………（ ）
A、相交 B、相切 C、相离 D、相切或相交CD3、在等腰△ABC中，AB=AC=2cm，若以
A为圆心，1cm为半径的圆与BC相切，则
∠ABC的度数为………………………（ ）
A、30° B、60° C、90° D、120°ACB22DA探索切线性质1.你能举出生活中直线与圆相交,相切,相离的实例吗?2.上面的三个图形是轴对称图形吗?如果是,你能画出它们的对称轴吗?驶向胜利的彼岸由此你能悟出点什么?探索切线性质如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.直径AB垂直于直线CD.驶向胜利的彼岸老师期望:
圆的对称性已经在你心中落地生根.小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.探索切线性质小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,驶向胜利的彼岸老师期望:
你能看明白(或掌握)用反证法说理的过程.则OM切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.如图
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.驶向胜利的彼岸切线的性质定理的应用1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?解:(1)过点C作CD⊥AB于D.∵AB=8cm,AC=4cm.∴∠A=60°.因此,当半径长为 cm时,AB与⊙C相切.驶向胜利的彼岸切线的性质定理的应用1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?当r=4cm时,dr,AB与⊙C相离;解:(2)由(1)可知,圆心到AB的距离d= cm,所以驶向胜利的彼岸切线的性质定理的应用1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围..2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少?.老师提示:硬币滚动一圈,圆心经过的路经是与直线平行的一条线段,其长度等于圆的周长.驶向胜利的彼岸挑战自我1.已知:如图,P是⊙O外一点,PA,PB都是⊙O的切线,A,B是切点.请你观察猜想,PA,PB有怎样的关系?并证明你的结论.2.由1所得的结论及证明过程,你还能发现那些新的结论?如果有,仍请你予以证明.老师提示:根据这个结论写出的命题称为切线长定理及其推论.挑战自我 P127:习题3.7 1，2，3 题祝你成功!驶向胜利的彼岸结束寄语具有丰富知识和经验的人，比只须一种知识和经验更容易产生新的联想和独到的见解。再见