第二十二章二次函数复习课件
文档属性
| 名称 | 第二十二章二次函数复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 385.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-21 20:01:13 | ||
图片预览









文档简介
课件65张PPT。二次函数1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 某果园有100棵橙子树,每一棵平均结600个橙子。现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子。(1)问题中有哪些变量?哪些是自变量?哪些是因变量?(2)假设果园增种x棵橙子树,那么果园共有
______棵橙子树,这时平均每棵树结_______个橙子。(3)如果果园橙子的总产量为y个,那么y与x
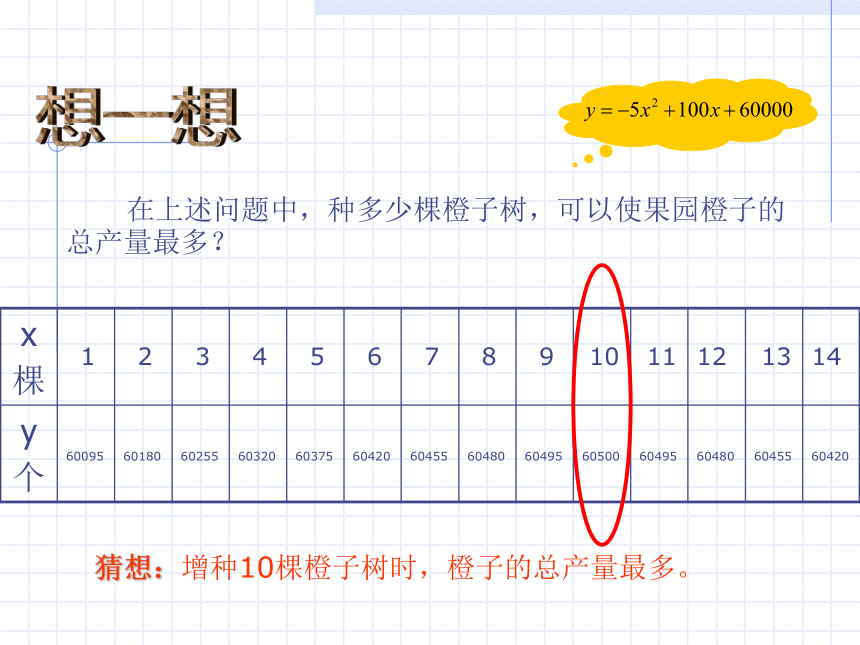
之间的关系式为_______________。想一想 在上述问题中,种多少棵橙子树,可以使果园橙子的总产量最多?12345678910111213146009560180602556032060375604206045560480604956050060495604806045560420猜想:增种10棵橙子树时,橙子的总产量最多。做一做 银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量。在我国,利率的调整是有中国人民银行根据国家经济发展的情况而决定的。 设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存。如果存款额是100元,那么两年后的本息和y(元)的表达式。
分两种情况—— (1)不考虑利息税;(2)考虑利息税。 一般地,形如y=ax2+bx+c(a、b、c是常数且a≠0)的函数叫做x的二次函数。例:圆的半径是1cm,假设半径增加 x cm时,圆的面积增加 y cm2。
(1)写出y与x之间的关系表达式;
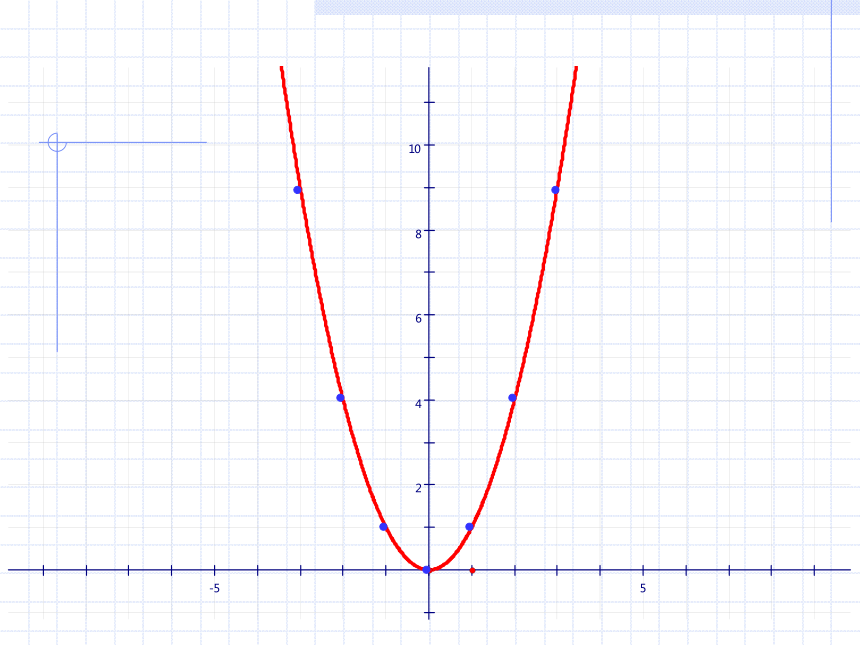
(2)当圆的半径分别增加1cm, cm,2cm时,圆的面积增加多少?1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程作二次函数 y=x2 的图象。(1)观察 y=x2 的表达式,选择适当的x值,并计算相应的y值,完成下表。(2)在直角坐标系中描点。(3)用光滑的曲线连接各点,便得到函数 y=x2 的图象。议一议 对于二次函数 y=x2 的图象,
(1)试描述图象的 形状。
(2)图象是轴对称图形吗?如果是,它的对称轴是什么?试找出几对对称点。
(3)图象与x轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x值的增大,y的值如何变化?当x>0时呢?
(5)当x取什么值时,y的值最小?最小值是什么? 二次函数 y=x2 的图象是一条抛物线,它的开口向上,且关于y轴对称。
在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随x的增大而增大。
函数图象有最低点(0,0)。对称轴与抛物线的交点 (抛物线的顶点)做一做二次函数 y=-x2 图象是什么形状?比较二次函数 y=x2 和 y=-x2 图象的异同:1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数。 有研究表明,晴天在某段公路上行驶时,速度为v(km/h)的汽车的刹车距离s(m)可以由公
式 确定。 雨天行驶时,这一公式为 。20406080100120v/(km/h)s/mO163248648096112128144(1)两个图象有什么相同与不同?(2)如果行车速度是60km/h,那么在雨天行驶和在晴天行驶相比,刹车距离相差多少米?做一做二次函数 y=2x2 的图象是什么形状?它与二次函数 y=x2 的图象有什么相同和不同?向上向上y轴y轴(0,0)(0,0)议一议(1)二次函数 y=2x2+1 的图象与二次函数 y=2x2 的图象有什么关系?向上向上y轴y轴(0,0)(0,1)议一议(2)二次函数 y=3x2-1 的图象与二次函数 y=3x2 的图象有什么关系?向上向上y轴y轴(0,0)(0,-1)在同一坐标系中画出下列各组函数的图象:作业1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程在同一坐标系中画出下列各组函数的图象:向上直线x=1(1,0)向上直线x=1(1,2)图象都是抛物线,形状相同,位置不同。在同一坐标系中画出下列各组函数的图象:向下直线x=-1(-1,0)向下直线x=-1(-1,-3)图象都是抛物线,形状相同,位置不同。 一般地,平移二次函数y=ax2的图象便可得到y=a(x-h)2+k的图象。向上向下直线x=h(h,k)(h,k)直线x=h练习向上向下向上向下向上向下向下向上直线x=-3直线x=-1直线x=3直线x=-1直线x=0直线x=2直线x=-4直线x=3y轴 下图所示桥梁的两条钢缆具有相同的抛物线形状。按照图中的直角坐标系,左面的一条抛物线可以用
y=0.0225x2+0.9x+10
表示,而且左右两条抛物线关于y轴对称。(1)钢缆的最低点到桥面的距离是多少? (2)两条钢缆最低点之间的距离是多少?求二次函数y=ax2+bx+c的对称轴和顶点坐标。练习根据公式确定下列二次函数图象的对称轴和顶点坐标:直线x=3直线x=8直线x=1.25直线x=0.751.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 长方形的周长为 20 cm,设它的一边长 x cm,面积为 y cm2。
y 随 x 变化而变化的规律是什么?分别用函数式、表格和图象表示出来。(1)用函数表达式表示:(2)用表格表示:(3)用图象表示:9876543219162124252421169(1)自变量x的取值范围是什么?(2)当x取何值时,长方形的面积最大? 当x=5时,y取最大值25。
即当长方形的长和宽都是5时,面积取最大值25。(3)描述y随x的变化而变化的情况。 当0 请你帮助分析,销售单价是多少时,可以获利最多?解:设销售单价为 元,则所获利润 某商店经营T恤衫,已知成批购进时单价是2.5元。根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件。
请你帮助分析,销售单价是多少时,可以获利最多?即所以销售单价是9.25元时,获利最多,达到9112.5元。做一做 某果园有100棵橙子树,每一棵平均结600个橙子。现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子。 假设果园增种x棵橙子树,那么果园共有______棵橙子树,这时平均每棵树结_______个橙子。 如果果园橙子的总产量为y个,那么y与x之间的关系式为_______________。议一议(1)利用函数图象描述橙子的总产量与增种橙子树的棵数之间的关系。O5101520x/棵60000601006020060300604006050060600y/个 当x<10时,橙子的总产量随增种橙子树的增加而增加; 当x>10时,橙子的总产量随增种橙子树的增加而减少。(2)增种多少棵橙子树,可以使橙子的总产量在60400个以上? 增种6~14棵,都可以使橙子的总产量在60400个以上。 若日销售量 y 是销售价 x 的一次函数。 (1)求出日销售量 y(件)与销售价 x(元)的函数关系式;(6分) (2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?(6分) 某产品每件成本10元,试销阶段每件产品的销售价 x(元)与产品的日销售量 y(件)之间的关系如下表:中考题选练国家基础教育课程改革贵阳实验区2004年升中试题 (1)设此一次函数解析式为 。(2)设每件产品的销售价应定为 x 元,所获销售利润为 w 元。则 产品的销售价应定为25元,此时每日获得最大销售利润为225元。则解得:k=-1,b=40。所以一次函数解析式为 。1分5分6分7分10分12分中考题选练 已知二次函数 y=0.5x2+bx+c 的图象经过点A(c,-2), 求证:这个二次函数图象的对称轴是直线 x=3。
题目中的黑色部分是一段被墨水污染了无法辨认的文字。
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象。若不能,请说明理由。
(2)请你根据已有的信息,在原题中的黑色部分添加一个适当的条件,把原题补充完整。国家基础教育课程改革青海省潢中县实验区2004年升中试题 中考题选练湖北省黄冈市2004年升中试题 心理学家研究发现:一般情况下,学生的注意力随着教师讲课时间的变化而变化,讲课开始时,学生的注意力y随时间t的变化规律有如下关系式:(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中?(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 如图,在一个直角三角形的内部作一个长方形ABCD,其中AB和AD分别在两直角边上。ABDC40m30m(1)设长方形的一边 AB = x m,那么AD边的长度如何表示?(2)设长方形的面积为 y m2,当 x 取何值时,y 的值最大?最大值是多少?当 时,议一议 如图,在一个直角三角形的内部作一个长方形ABCD,其中AB和AD分别在两直角边上。ABDC40m30m 如果设AD边的长为 x m,那么问题的结果怎样?当 时,FE做一做 某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长为15m。当 x等于多少时,窗户通过的光线最多(结果精确到0.01 m2 )?xxy设窗户的面积为 ,则 。 当 时, 。此时,窗户通过的光线最多。议一议 回顾《何时获得最大利润》和《最大面积是多少》这两节解决问题的过程,试总结解决此类问题的基本思路。(1)理解问题;(2)分析问题中的变量和常量,以及它们之间的关系;(3)用数学的方式表示它们之间的关系;(4)数学求解;(5)检验结果的合理性、拓展等。1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 竖直上抛物体的高度 h(m) 与运动时间 t(s) 的关系可以用公式 h=-5t2+v0t+h0 表示,其中 h0(m) 是抛出时的高度, v0(m/s) 是抛出时的速度。 一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度 h(m) 与运动时间 t(s) 的关系如图所示,那么
(1)h与t的关系式是什么?
(2)小球经过多少秒后落地?O123456781020304050607080h/mt/s议一议 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示:(1)每个图象与x轴有几个交点?(2)方程 x2+2x=0,x2-2x+1=0,y=x2-2x+2=0根的情况怎样?(3)可以得出什么结论?一元二次方程二次函数二次函数的图象有两个不等实根 ,有两个相等实根没有实根图象与x轴没有交点图象与x轴有两个交点图象与x轴有一个交点O123456781020304050607080h/mt/s想一想 在前面的小球上抛问题中,何时小球离地面的高度是60m?方法一:利用图象方法二:解方程课本67页随堂练习(3)
方程 -4.9t2+19.6t=0 的根的实际意义
——足球离开地面及落地的时间
方程 -4.9t2+19.6t=14.7 的根的实际意义
——足球离地面高度是14.7m时的时间利用二次函数的图象估计一元二次方程 的根。 由图象可知方程有两个根,一个在-5和-4之间,另一个在2和3之间。(1)求-5和-4之间的根。当 x=-4.1 时,y=-1.39当 x=-4.2 时,y=-0.76当 x=-4.3时,y=-0.11当 x=-4.4 时,y=0.56因此,x=-4.3是方程的一个近似根。(2)求2和3之间的根。当 x=2.1 时,y=-1.39当 x=2.2 时,y=-0.76当 x=2.3时,y=-0.11当 x=2.4 时,y=0.56因此,x=2.3是方程的一个近似根。
______棵橙子树,这时平均每棵树结_______个橙子。(3)如果果园橙子的总产量为y个,那么y与x
之间的关系式为_______________。想一想 在上述问题中,种多少棵橙子树,可以使果园橙子的总产量最多?12345678910111213146009560180602556032060375604206045560480604956050060495604806045560420猜想:增种10棵橙子树时,橙子的总产量最多。做一做 银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量。在我国,利率的调整是有中国人民银行根据国家经济发展的情况而决定的。 设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存。如果存款额是100元,那么两年后的本息和y(元)的表达式。
分两种情况—— (1)不考虑利息税;(2)考虑利息税。 一般地,形如y=ax2+bx+c(a、b、c是常数且a≠0)的函数叫做x的二次函数。例:圆的半径是1cm,假设半径增加 x cm时,圆的面积增加 y cm2。
(1)写出y与x之间的关系表达式;
(2)当圆的半径分别增加1cm, cm,2cm时,圆的面积增加多少?1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程作二次函数 y=x2 的图象。(1)观察 y=x2 的表达式,选择适当的x值,并计算相应的y值,完成下表。(2)在直角坐标系中描点。(3)用光滑的曲线连接各点,便得到函数 y=x2 的图象。议一议 对于二次函数 y=x2 的图象,
(1)试描述图象的 形状。
(2)图象是轴对称图形吗?如果是,它的对称轴是什么?试找出几对对称点。
(3)图象与x轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x值的增大,y的值如何变化?当x>0时呢?
(5)当x取什么值时,y的值最小?最小值是什么? 二次函数 y=x2 的图象是一条抛物线,它的开口向上,且关于y轴对称。
在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随x的增大而增大。
函数图象有最低点(0,0)。对称轴与抛物线的交点 (抛物线的顶点)做一做二次函数 y=-x2 图象是什么形状?比较二次函数 y=x2 和 y=-x2 图象的异同:1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数。 有研究表明,晴天在某段公路上行驶时,速度为v(km/h)的汽车的刹车距离s(m)可以由公
式 确定。 雨天行驶时,这一公式为 。20406080100120v/(km/h)s/mO163248648096112128144(1)两个图象有什么相同与不同?(2)如果行车速度是60km/h,那么在雨天行驶和在晴天行驶相比,刹车距离相差多少米?做一做二次函数 y=2x2 的图象是什么形状?它与二次函数 y=x2 的图象有什么相同和不同?向上向上y轴y轴(0,0)(0,0)议一议(1)二次函数 y=2x2+1 的图象与二次函数 y=2x2 的图象有什么关系?向上向上y轴y轴(0,0)(0,1)议一议(2)二次函数 y=3x2-1 的图象与二次函数 y=3x2 的图象有什么关系?向上向上y轴y轴(0,0)(0,-1)在同一坐标系中画出下列各组函数的图象:作业1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程在同一坐标系中画出下列各组函数的图象:向上直线x=1(1,0)向上直线x=1(1,2)图象都是抛物线,形状相同,位置不同。在同一坐标系中画出下列各组函数的图象:向下直线x=-1(-1,0)向下直线x=-1(-1,-3)图象都是抛物线,形状相同,位置不同。 一般地,平移二次函数y=ax2的图象便可得到y=a(x-h)2+k的图象。向上向下直线x=h(h,k)(h,k)直线x=h练习向上向下向上向下向上向下向下向上直线x=-3直线x=-1直线x=3直线x=-1直线x=0直线x=2直线x=-4直线x=3y轴 下图所示桥梁的两条钢缆具有相同的抛物线形状。按照图中的直角坐标系,左面的一条抛物线可以用
y=0.0225x2+0.9x+10
表示,而且左右两条抛物线关于y轴对称。(1)钢缆的最低点到桥面的距离是多少? (2)两条钢缆最低点之间的距离是多少?求二次函数y=ax2+bx+c的对称轴和顶点坐标。练习根据公式确定下列二次函数图象的对称轴和顶点坐标:直线x=3直线x=8直线x=1.25直线x=0.751.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 长方形的周长为 20 cm,设它的一边长 x cm,面积为 y cm2。
y 随 x 变化而变化的规律是什么?分别用函数式、表格和图象表示出来。(1)用函数表达式表示:(2)用表格表示:(3)用图象表示:9876543219162124252421169(1)自变量x的取值范围是什么?(2)当x取何值时,长方形的面积最大? 当x=5时,y取最大值25。
即当长方形的长和宽都是5时,面积取最大值25。(3)描述y随x的变化而变化的情况。 当0
请你帮助分析,销售单价是多少时,可以获利最多?即所以销售单价是9.25元时,获利最多,达到9112.5元。做一做 某果园有100棵橙子树,每一棵平均结600个橙子。现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子。 假设果园增种x棵橙子树,那么果园共有______棵橙子树,这时平均每棵树结_______个橙子。 如果果园橙子的总产量为y个,那么y与x之间的关系式为_______________。议一议(1)利用函数图象描述橙子的总产量与增种橙子树的棵数之间的关系。O5101520x/棵60000601006020060300604006050060600y/个 当x<10时,橙子的总产量随增种橙子树的增加而增加; 当x>10时,橙子的总产量随增种橙子树的增加而减少。(2)增种多少棵橙子树,可以使橙子的总产量在60400个以上? 增种6~14棵,都可以使橙子的总产量在60400个以上。 若日销售量 y 是销售价 x 的一次函数。 (1)求出日销售量 y(件)与销售价 x(元)的函数关系式;(6分) (2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?(6分) 某产品每件成本10元,试销阶段每件产品的销售价 x(元)与产品的日销售量 y(件)之间的关系如下表:中考题选练国家基础教育课程改革贵阳实验区2004年升中试题 (1)设此一次函数解析式为 。(2)设每件产品的销售价应定为 x 元,所获销售利润为 w 元。则 产品的销售价应定为25元,此时每日获得最大销售利润为225元。则解得:k=-1,b=40。所以一次函数解析式为 。1分5分6分7分10分12分中考题选练 已知二次函数 y=0.5x2+bx+c 的图象经过点A(c,-2), 求证:这个二次函数图象的对称轴是直线 x=3。
题目中的黑色部分是一段被墨水污染了无法辨认的文字。
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象。若不能,请说明理由。
(2)请你根据已有的信息,在原题中的黑色部分添加一个适当的条件,把原题补充完整。国家基础教育课程改革青海省潢中县实验区2004年升中试题 中考题选练湖北省黄冈市2004年升中试题 心理学家研究发现:一般情况下,学生的注意力随着教师讲课时间的变化而变化,讲课开始时,学生的注意力y随时间t的变化规律有如下关系式:(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中?(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 如图,在一个直角三角形的内部作一个长方形ABCD,其中AB和AD分别在两直角边上。ABDC40m30m(1)设长方形的一边 AB = x m,那么AD边的长度如何表示?(2)设长方形的面积为 y m2,当 x 取何值时,y 的值最大?最大值是多少?当 时,议一议 如图,在一个直角三角形的内部作一个长方形ABCD,其中AB和AD分别在两直角边上。ABDC40m30m 如果设AD边的长为 x m,那么问题的结果怎样?当 时,FE做一做 某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长为15m。当 x等于多少时,窗户通过的光线最多(结果精确到0.01 m2 )?xxy设窗户的面积为 ,则 。 当 时, 。此时,窗户通过的光线最多。议一议 回顾《何时获得最大利润》和《最大面积是多少》这两节解决问题的过程,试总结解决此类问题的基本思路。(1)理解问题;(2)分析问题中的变量和常量,以及它们之间的关系;(3)用数学的方式表示它们之间的关系;(4)数学求解;(5)检验结果的合理性、拓展等。1.二次函数所描述的关系2.结识抛物线3.刹车距离与二次函数4.二次函数的图象5.用三种方式表示二次函数6.何时获得最大利润7.最大面积是多少8.二次函数与一元二次方程 竖直上抛物体的高度 h(m) 与运动时间 t(s) 的关系可以用公式 h=-5t2+v0t+h0 表示,其中 h0(m) 是抛出时的高度, v0(m/s) 是抛出时的速度。 一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度 h(m) 与运动时间 t(s) 的关系如图所示,那么
(1)h与t的关系式是什么?
(2)小球经过多少秒后落地?O123456781020304050607080h/mt/s议一议 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示:(1)每个图象与x轴有几个交点?(2)方程 x2+2x=0,x2-2x+1=0,y=x2-2x+2=0根的情况怎样?(3)可以得出什么结论?一元二次方程二次函数二次函数的图象有两个不等实根 ,有两个相等实根没有实根图象与x轴没有交点图象与x轴有两个交点图象与x轴有一个交点O123456781020304050607080h/mt/s想一想 在前面的小球上抛问题中,何时小球离地面的高度是60m?方法一:利用图象方法二:解方程课本67页随堂练习(3)
方程 -4.9t2+19.6t=0 的根的实际意义
——足球离开地面及落地的时间
方程 -4.9t2+19.6t=14.7 的根的实际意义
——足球离地面高度是14.7m时的时间利用二次函数的图象估计一元二次方程 的根。 由图象可知方程有两个根,一个在-5和-4之间,另一个在2和3之间。(1)求-5和-4之间的根。当 x=-4.1 时,y=-1.39当 x=-4.2 时,y=-0.76当 x=-4.3时,y=-0.11当 x=-4.4 时,y=0.56因此,x=-4.3是方程的一个近似根。(2)求2和3之间的根。当 x=2.1 时,y=-1.39当 x=2.2 时,y=-0.76当 x=2.3时,y=-0.11当 x=2.4 时,y=0.56因此,x=2.3是方程的一个近似根。
同课章节目录
