平行线分线段成比例(上海市闵行区)(无答案)
文档属性
| 名称 | 平行线分线段成比例(上海市闵行区)(无答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 65.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-20 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
初三暑期盛华学校数学讲义(一)
平行线分线段成比例
1、 定理汇总:
1、 平行线分线段成比例定理
定理:三条平行线截两条直线,所得的对应线段成比例.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
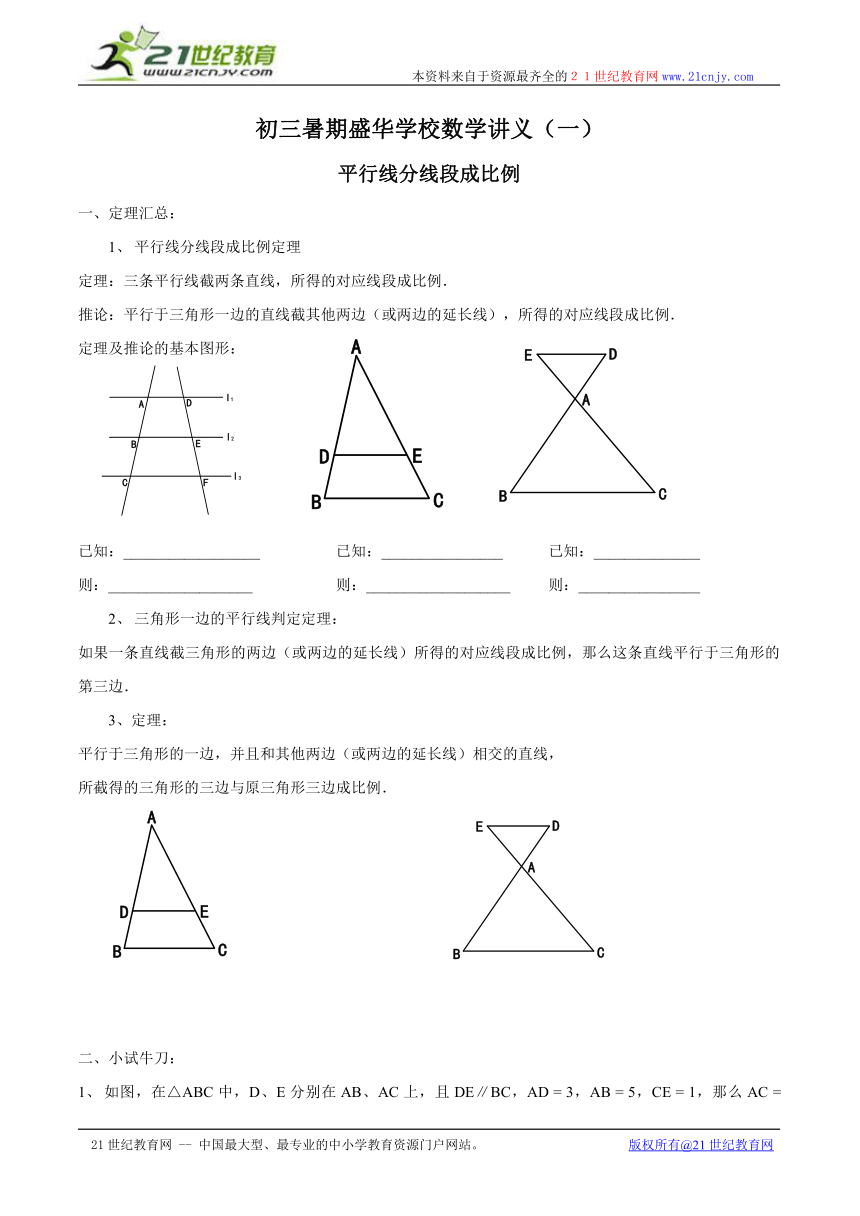
定理及推论的基本图形:
已知:__________________ 已知:________________ 已知:______________
则:___________________ 则:___________________ 则:________________
2、 三角形一边的平行线判定定理:
如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
3、定理:
平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,
所截得的三角形的三边与原三角形三边成比例.
二、小试牛刀:
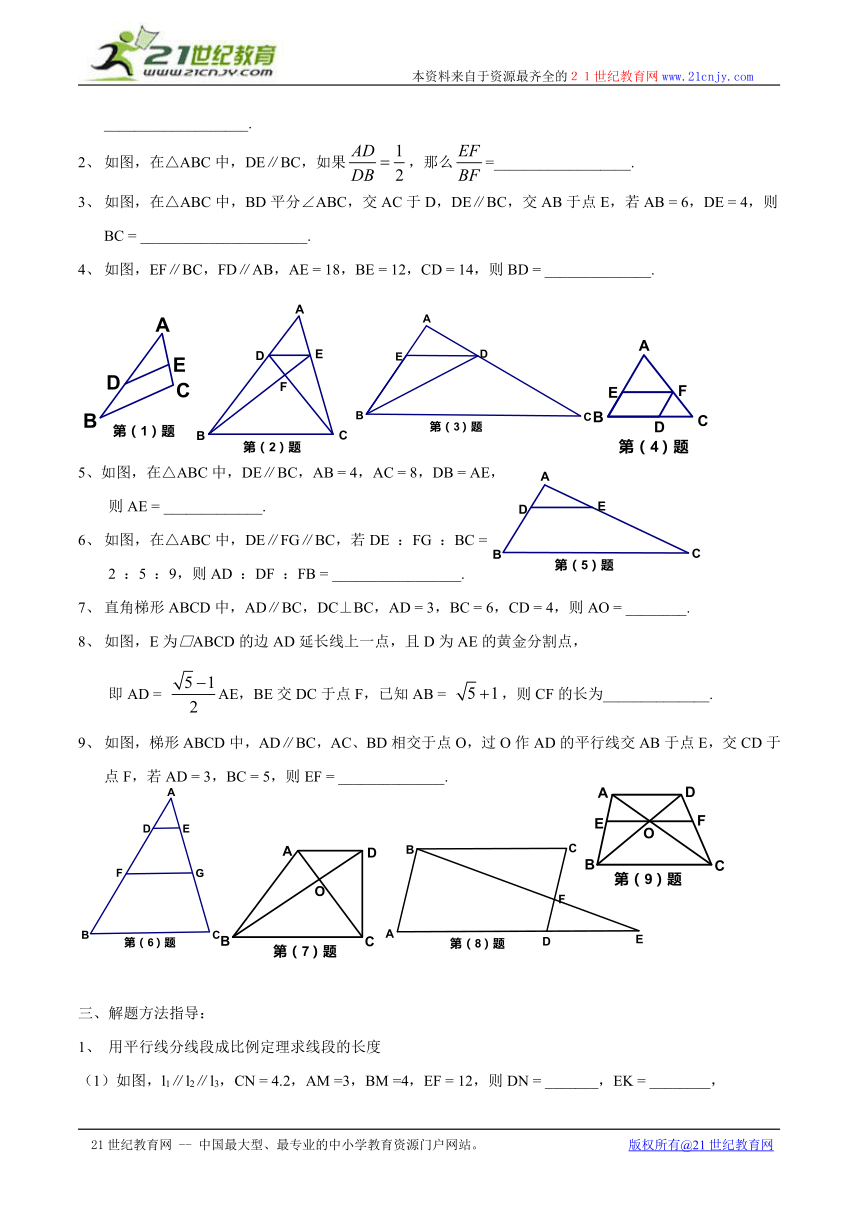
1、 如图,在△ABC中,D、E分别在AB、AC上,且DE∥BC,AD = 3,AB = 5,CE = 1,那么AC = ___________________.
2、 如图,在△ABC中,DE∥BC,如果,那么=__________________.
3、 如图,在△ABC中,BD平分∠ABC,交AC于D,DE∥BC,交AB于点E,若AB = 6,DE = 4,则BC = ______________________.
4、 如图,EF∥BC,FD∥AB,AE = 18,BE = 12,CD = 14,则BD = ______________.
5、如图,在△ABC中,DE∥BC,AB = 4,AC = 8,DB = AE,
则AE = _____________.
6、 如图,在△ABC中,DE∥FG∥BC,若DE :FG :BC =
2 :5 :9,则AD :DF :FB = _________________.
7、 直角梯形ABCD中,AD∥BC,DC⊥BC,AD = 3,BC = 6,CD = 4,则AO = ________.
8、 如图,E为□ABCD的边AD延长线上一点,且D为AE的黄金分割点,
即AD = AE,BE交DC于点F,已知AB = ,则CF的长为______________.
9、 如图,梯形ABCD中,AD∥BC,AC、BD相交于点O,过O作AD的平行线交AB于点E,交CD于点F,若AD = 3,BC = 5,则EF = ______________.
3、 解题方法指导:
1、 用平行线分线段成比例定理求线段的长度
(1)如图,l1∥l2∥l3,CN = 4.2,AM =3,BM =4,EF = 12,则DN = _______,EK = ________,
(2)如图,AB⊥BC于B,EF⊥BC于F,DC⊥BC于C,AB = 4,DC = 14,
且BF :FC = 2 :3,则EF的值为________________________,
(3) 如图,在矩形ABCD中,AB = 6,AD = 8,点E、F为BC的三等分点,则BG = ______,GH=_____________,HD = ______________,
(4) 如图,AB∥EF∥DC,AB = 6cm,DC = 9cm,则EF = ____________________,
(5)
(6) 如图,H、G是ABCD对角线BD上的三等分点,延长AH交BC于点E,延长EG交AD于点F,则AF :FD = _________________________,
(7) 在△ABC中,D为BC的中点,F为AC上一点,且CF :AF = 1 :2,BF交AD于点E,则=____________________,
(8) 在正方形ABCD中,点E、F分别在边AD、AB上,且AE = BF =AB,EF与AC相交于点H,则EH :FH = ____________,设AB = x,四边形BCHF的面积为y,则y关于x的函数解析式为__________________________,
(9) 已知如图,E是ABCD中BC上的任意一点,DE与AB的延长线交于点F,则=____________________。
2、运用平行线分线段成比例定理解决求证比例式或乘积式的题型
(1)已知:E为ABCD边CD延长线上的一点,联结BE交AC于O,
求证:BO2 = OF·OE
(2)如图,已知E是△ABC中AC边的中点,过点E的任意直线交AB于点D,
交BC的延长线于点F
求证:BD·CF = BF·AD
(3)已知:如图,△ABC中,DE∥BC,CD、BE交于点O,
过点O作MN∥BC,分别交AB、AC于点M、N
求证:
(4)如图,已知△ABC中,∠ACB = 90°,以BC为边向外作正方形BCDE,
联结AE交BC于点F,作FG∥AC交AB于点G
求证:FC = FG
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
初三暑期盛华学校数学讲义(一)
平行线分线段成比例
1、 定理汇总:
1、 平行线分线段成比例定理
定理:三条平行线截两条直线,所得的对应线段成比例.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
定理及推论的基本图形:
已知:__________________ 已知:________________ 已知:______________
则:___________________ 则:___________________ 则:________________
2、 三角形一边的平行线判定定理:
如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
3、定理:
平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,
所截得的三角形的三边与原三角形三边成比例.
二、小试牛刀:
1、 如图,在△ABC中,D、E分别在AB、AC上,且DE∥BC,AD = 3,AB = 5,CE = 1,那么AC = ___________________.
2、 如图,在△ABC中,DE∥BC,如果,那么=__________________.
3、 如图,在△ABC中,BD平分∠ABC,交AC于D,DE∥BC,交AB于点E,若AB = 6,DE = 4,则BC = ______________________.
4、 如图,EF∥BC,FD∥AB,AE = 18,BE = 12,CD = 14,则BD = ______________.
5、如图,在△ABC中,DE∥BC,AB = 4,AC = 8,DB = AE,
则AE = _____________.
6、 如图,在△ABC中,DE∥FG∥BC,若DE :FG :BC =
2 :5 :9,则AD :DF :FB = _________________.
7、 直角梯形ABCD中,AD∥BC,DC⊥BC,AD = 3,BC = 6,CD = 4,则AO = ________.
8、 如图,E为□ABCD的边AD延长线上一点,且D为AE的黄金分割点,
即AD = AE,BE交DC于点F,已知AB = ,则CF的长为______________.
9、 如图,梯形ABCD中,AD∥BC,AC、BD相交于点O,过O作AD的平行线交AB于点E,交CD于点F,若AD = 3,BC = 5,则EF = ______________.
3、 解题方法指导:
1、 用平行线分线段成比例定理求线段的长度
(1)如图,l1∥l2∥l3,CN = 4.2,AM =3,BM =4,EF = 12,则DN = _______,EK = ________,
(2)如图,AB⊥BC于B,EF⊥BC于F,DC⊥BC于C,AB = 4,DC = 14,
且BF :FC = 2 :3,则EF的值为________________________,
(3) 如图,在矩形ABCD中,AB = 6,AD = 8,点E、F为BC的三等分点,则BG = ______,GH=_____________,HD = ______________,
(4) 如图,AB∥EF∥DC,AB = 6cm,DC = 9cm,则EF = ____________________,
(5)
(6) 如图,H、G是ABCD对角线BD上的三等分点,延长AH交BC于点E,延长EG交AD于点F,则AF :FD = _________________________,
(7) 在△ABC中,D为BC的中点,F为AC上一点,且CF :AF = 1 :2,BF交AD于点E,则=____________________,
(8) 在正方形ABCD中,点E、F分别在边AD、AB上,且AE = BF =AB,EF与AC相交于点H,则EH :FH = ____________,设AB = x,四边形BCHF的面积为y,则y关于x的函数解析式为__________________________,
(9) 已知如图,E是ABCD中BC上的任意一点,DE与AB的延长线交于点F,则=____________________。
2、运用平行线分线段成比例定理解决求证比例式或乘积式的题型
(1)已知:E为ABCD边CD延长线上的一点,联结BE交AC于O,
求证:BO2 = OF·OE
(2)如图,已知E是△ABC中AC边的中点,过点E的任意直线交AB于点D,
交BC的延长线于点F
求证:BD·CF = BF·AD
(3)已知:如图,△ABC中,DE∥BC,CD、BE交于点O,
过点O作MN∥BC,分别交AB、AC于点M、N
求证:
(4)如图,已知△ABC中,∠ACB = 90°,以BC为边向外作正方形BCDE,
联结AE交BC于点F,作FG∥AC交AB于点G
求证:FC = FG
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
