平行线分线段成比例拓展(上海市闵行区)(无答案)
文档属性
| 名称 | 平行线分线段成比例拓展(上海市闵行区)(无答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 41.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-20 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
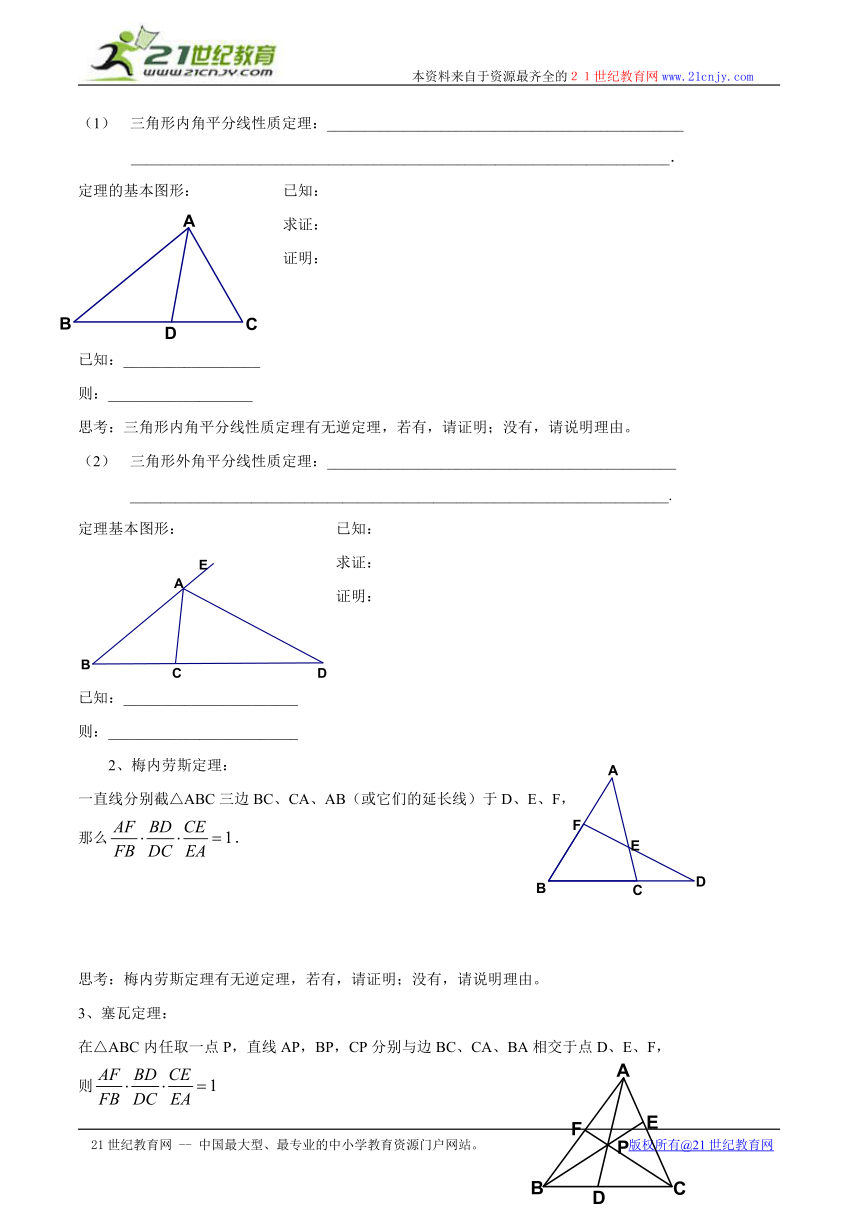
初三暑期盛华学校数学讲义(二)
平行线分线段成比例定理的拓展
一、小试牛刀:
1、 如图,在平行四边形ABCD中,E是BC边上的点,AE交BD于点F,如果,那么_____________________.
2、 如图,在△ABC中,AB = BC = 2,∠B = 45°,四边形DEFG是△ABC的内接正方形,点D、E在BC上,点G、F分别在AB、AC上,则正方形DEFG的边长为____________..
3、 如图,已知在平行四边形ABCD中,对角线AC和BD相交于点O,在BC上取点E,使EC =BC,DE和AC相交于点F,则AO :OF :FC =__________________.
4、 如图,在梯形ABCD中,AD∥BC,AD = 3,BC = 5,点E在AB上,
且AE : EB = 2 : 3,过点E作EF∥BC交CD于点F,则EF = ______________________.
5、利用平行线分线段成比例定理作图
(1)把线段AB分成3 :4两部分
(2)已知线段a,b,c,求作线段x,使x =
二、定理拓展:
1、 三角形的角平分线性质
(1) 三角形内角平分线性质定理:_______________________________________________
_______________________________________________________________________.
定理的基本图形: 已知:
求证:
证明:
已知:__________________
则:___________________
思考:三角形内角平分线性质定理有无逆定理,若有,请证明;没有,请说明理由。
(2) 三角形外角平分线性质定理:______________________________________________
_______________________________________________________________________.
定理基本图形: 已知:
求证:
证明:
已知:_______________________
则:_________________________
2、梅内劳斯定理:
一直线分别截△ABC三边BC、CA、AB(或它们的延长线)于D、E、F,
那么.
思考:梅内劳斯定理有无逆定理,若有,请证明;没有,请说明理由。
3、塞瓦定理:
在△ABC内任取一点P,直线AP,BP,CP分别与边BC、CA、BA相交于点D、E、F,
则
思考:塞瓦定理有无逆定理,若有,请证明;没有,请说明理由。
三、定理应用:
1.已知:△ABC中,BE和CF为角平分线,且EF∥BC
求证:△ABC是等腰三角形
2.已知△ABC的三边AB = 11cm,AC = 7cm,BC = 6cm,AD、AD’是内、外角平分线,
求DD’的长。
3.已知:在△ABC中,AB≠AC,D、E分别为AB、AC上的点,且BD = CE,DE的延长线交BC的延长线于点F
求证:AC·EF = AB·DF
4.已知:如图,四边形ABCD为平行四边形,其中DC = 12cm,CE = 4cm,CB = 10cm
求CF的长。
5.已知△ABC的∠BAC的外角平分线与边BC的延长线交于点P,∠ABC的平分线与边CA交于点Q,∠ACB的平分线与边AB交于点R,
求证:P、Q、R三点共线。
6.求证:三角形三条中线(内角平分线)相交于同一点。
7.已知:若E、F是△ABC的边AC、AB上的点,且有AF :AB = CE :CA = 1 :4,BE 交CF于点P,AP交BC于点D
求:CD :CB的值。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
初三暑期盛华学校数学讲义(二)
平行线分线段成比例定理的拓展
一、小试牛刀:
1、 如图,在平行四边形ABCD中,E是BC边上的点,AE交BD于点F,如果,那么_____________________.
2、 如图,在△ABC中,AB = BC = 2,∠B = 45°,四边形DEFG是△ABC的内接正方形,点D、E在BC上,点G、F分别在AB、AC上,则正方形DEFG的边长为____________..
3、 如图,已知在平行四边形ABCD中,对角线AC和BD相交于点O,在BC上取点E,使EC =BC,DE和AC相交于点F,则AO :OF :FC =__________________.
4、 如图,在梯形ABCD中,AD∥BC,AD = 3,BC = 5,点E在AB上,
且AE : EB = 2 : 3,过点E作EF∥BC交CD于点F,则EF = ______________________.
5、利用平行线分线段成比例定理作图
(1)把线段AB分成3 :4两部分
(2)已知线段a,b,c,求作线段x,使x =
二、定理拓展:
1、 三角形的角平分线性质
(1) 三角形内角平分线性质定理:_______________________________________________
_______________________________________________________________________.
定理的基本图形: 已知:
求证:
证明:
已知:__________________
则:___________________
思考:三角形内角平分线性质定理有无逆定理,若有,请证明;没有,请说明理由。
(2) 三角形外角平分线性质定理:______________________________________________
_______________________________________________________________________.
定理基本图形: 已知:
求证:
证明:
已知:_______________________
则:_________________________
2、梅内劳斯定理:
一直线分别截△ABC三边BC、CA、AB(或它们的延长线)于D、E、F,
那么.
思考:梅内劳斯定理有无逆定理,若有,请证明;没有,请说明理由。
3、塞瓦定理:
在△ABC内任取一点P,直线AP,BP,CP分别与边BC、CA、BA相交于点D、E、F,
则
思考:塞瓦定理有无逆定理,若有,请证明;没有,请说明理由。
三、定理应用:
1.已知:△ABC中,BE和CF为角平分线,且EF∥BC
求证:△ABC是等腰三角形
2.已知△ABC的三边AB = 11cm,AC = 7cm,BC = 6cm,AD、AD’是内、外角平分线,
求DD’的长。
3.已知:在△ABC中,AB≠AC,D、E分别为AB、AC上的点,且BD = CE,DE的延长线交BC的延长线于点F
求证:AC·EF = AB·DF
4.已知:如图,四边形ABCD为平行四边形,其中DC = 12cm,CE = 4cm,CB = 10cm
求CF的长。
5.已知△ABC的∠BAC的外角平分线与边BC的延长线交于点P,∠ABC的平分线与边CA交于点Q,∠ACB的平分线与边AB交于点R,
求证:P、Q、R三点共线。
6.求证:三角形三条中线(内角平分线)相交于同一点。
7.已知:若E、F是△ABC的边AC、AB上的点,且有AF :AB = CE :CA = 1 :4,BE 交CF于点P,AP交BC于点D
求:CD :CB的值。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
