第二章 一元一次不等式与一元一次不等式组 小结与复习 同步课件(共25张PPT)
文档属性
| 名称 | 第二章 一元一次不等式与一元一次不等式组 小结与复习 同步课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:47 | ||
图片预览



文档简介
(共25张PPT)
第二章
《一元一次不等式与一元一次不等式组》
小结与复习
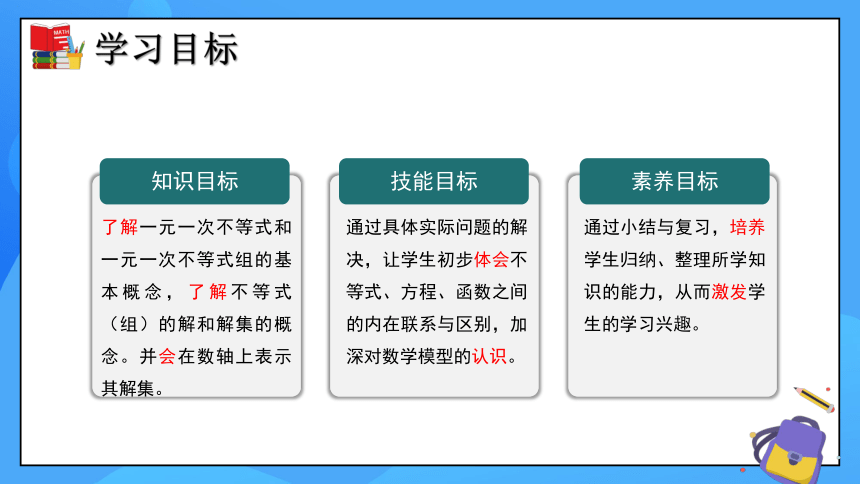
素养目标
技能目标
知识目标
了解一元一次不等式和一元一次不等式组的基本概念,了解不等式(组)的解和解集的概念。并会在数轴上表示其解集。
通过具体实际问题的解决,让学生初步体会不等式、方程、函数之间的内在联系与区别,加深对数学模型的认识。
通过小结与复习,培养学生归纳、整理所学知识的能力,从而激发学生的学习兴趣。
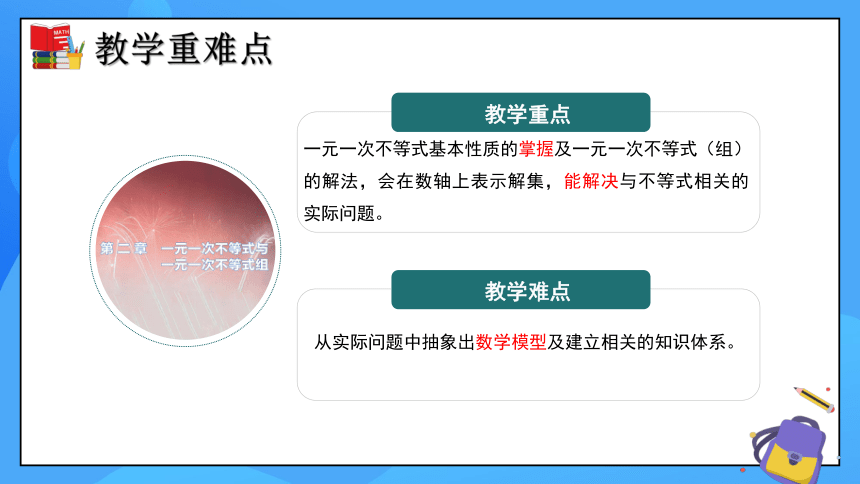
教学重点
教学难点
一元一次不等式基本性质的掌握及一元一次不等式(组)的解法,会在数轴上表示解集,能解决与不等式相关的实际问题。
从实际问题中抽象出数学模型及建立相关的知识体系。
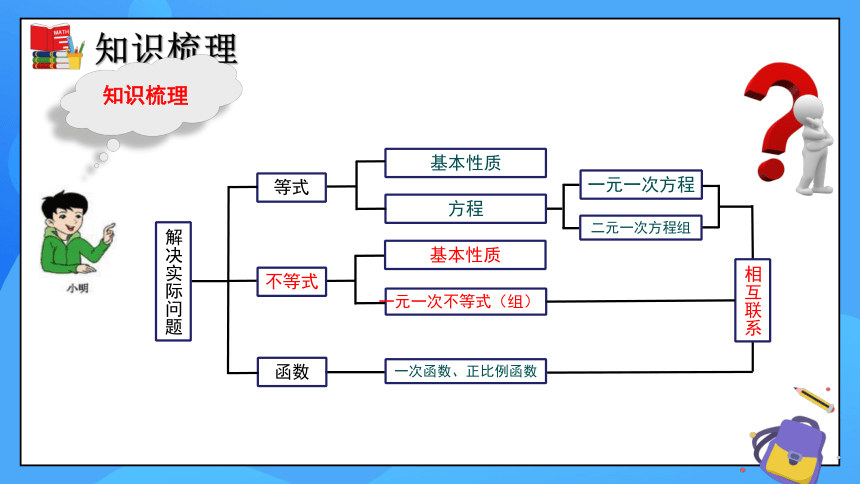
基本性质
方程
等式
一次函数、正比例函数
函数
知识梳理
基本性质
一元一次不等式(组)
不等式
解决实际问题
一元一次方程
二元一次方程组
相互联系
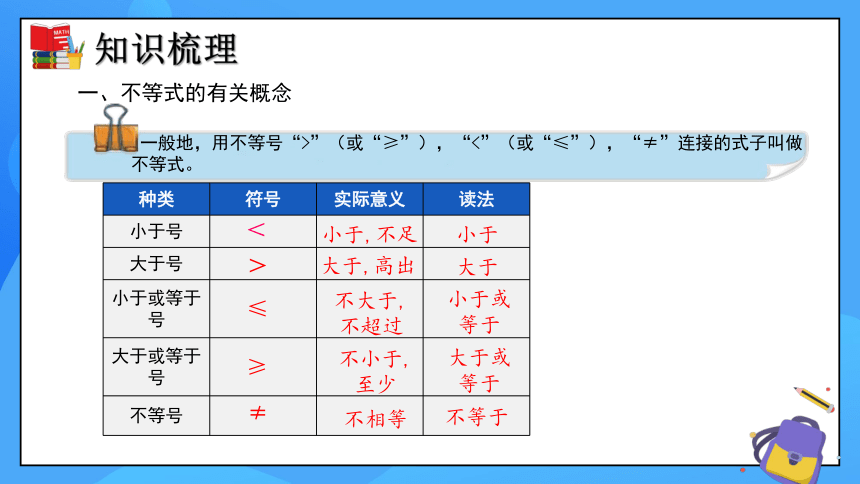
一、不等式的有关概念
一般地,用不等号“>”(或“≥”),“<”(或“≤”),“≠”连接的式子叫做不等式。
种类 符号 实际意义 读法
小于号
大于号
小于或等于号
大于或等于号
不等号
<
小于,不足
小于
>
大于,高出
大于
≤
不大于,不超过
小于或等于
≥
不小于,至少
大于或等于
≠
不相等
不等于
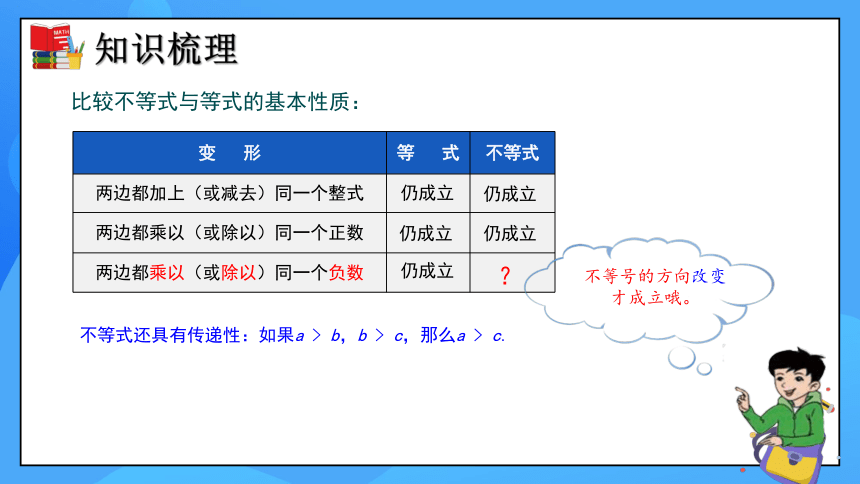
比较不等式与等式的基本性质:
变 形 等 式 不等式
两边都加上(或减去)同一个整式
两边都乘以(或除以)同一个正数
两边都乘以(或除以)同一个负数
仍成立
仍成立
仍成立
仍成立
仍成立
?
不等号的方向改变才成立哦。
不等式还具有传递性:如果a > b,b > c,那么a > c.
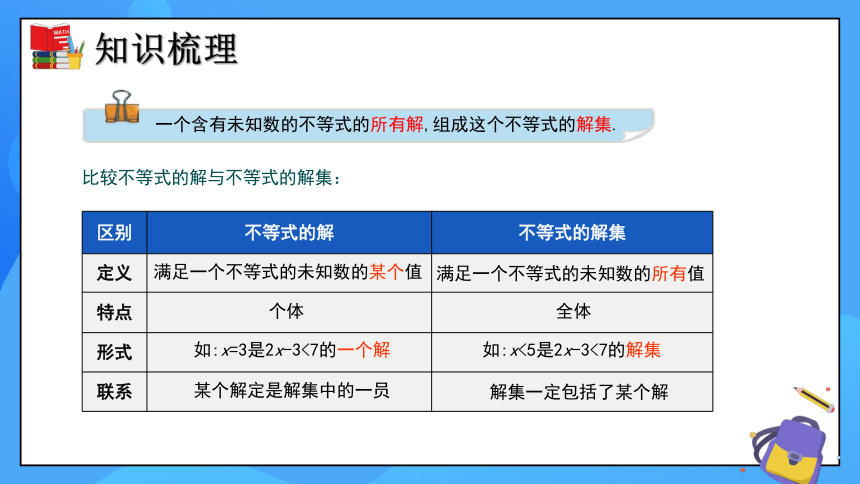
一个含有未知数的不等式的所有解,组成这个不等式的解集.
比较不等式的解与不等式的解集:
区别 不等式的解 不等式的解集
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
①左右两边都是整式;
②只有一个未知数,且未知数的最高次数是1;
③用不等号连接的式子.
一元一次不等式的特征:
一元一次不等式的定义:不等式的左右两边都是整式,只含一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
解一元一次方程的步骤是什么
类似的,解一元一次不等式的步骤和解一元一次方程一样。在运用性质3时要特别注意:改变不等号的方向.
解一元一次方程的步骤:
①去分母;
②去括号;
③移项;
④合并同类项;
⑤系数化为1.
用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心点表示;不包含在解集中,则用空心点表示.
(3)定方向:相对于边界点,大于向右画,小于向左画.
用一元一次不等式解决实际问题的一般步骤:
(1)审:认真审题找出不等关系;
(2)设:设出适当未知数;
(3)列:根据题中的不等关系,列出不等式;
(4)解:解所列的不等式;
(5)答:根据实际情况写出答案.
在应用一元一次不等式解决实际问题时,要抓住题中的关键词,如“大于”“不大于”“至少”“不超过”等.
一元一次不等式与一次函数在决策型应用题中的应用
实际问题
写出两个函数表达式
列不等式
解不等式
画出图象
分析图象
解决问题
图象法
代数法
解决问题
要选择合理、简捷的方法解题。
一元一次不等式与一次函数在决策型应用题中的应用
利用图象法解不等式步骤:
(1)作出不等式左、右两边所对应的两个一次函数的图象.
(2)确定两个一次函数图象的交点坐标.
(3)找出哪段函数图象在上方,哪段函数在下方,从而确定自变量的取值范围.
一元一次不等式与一次函数在决策型应用题中的应用
刻画运动变化的规律需要用函数模型;
刻画变化过程中同类量之间的大小,需要用不等式模型;
刻画运动变化过程中的某一瞬间需要用方程模型。
解决实际问题时,要合理选择这三种数学模型.
确定一个不等式组是一元一次不等式需要满足三点:
(1)不等式组中只有一个未知数;
(2)未知数的最高次数是1;
(3)组成不等式的代数式都是整式.
在数轴上表示 解 集 口 诀
a
b
x > b
a
b
x < a
a
b
a < x < b
a
b
无解
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
同大取大
同小取小
大小小大中间找
大大小小无处找
1. 下列命题正确的是 ( )
A.若a>b,bc B.若a>b,则ac>bc
C.若a>b,则ac2>bc2 D.若ac2>bc2,则a>b
D
解析:
选项A,由a>b,bc ;
选项B,a>b,当c=0时,ac=bc,不能根据不等式的性质确定ac>bc ;
选项C,a>b,当c=0时,ac2=bc2,不能根据不等式的性质确定ac2>bc2;
选项D,ac2>bc2,隐含c≠0 ,可以根据不等式的性质在不等式的两边同时除以正数c2,从而确定a>b.
2. 解不等式 并把解集在数轴上表示出来.
解: 去分母,得3(x-1) ≤ 1+x,
整理,得2x ≤ 4,
∴ x ≤ 2.
解集在数轴上表示如下图
2
1
-1
0
[思想方法] 明确不等式的解与解集的区别,用数轴表示不等式的解集时,要注意两点:一是分界点,二是方向.
3 . 解不等式组 把解集在数轴上表示出来,并将解集中的整数解写出来.
解:解不等式 ,得 x≤3,
解不等式 ,得
解集在数轴上表示如下:
通过观察数轴可知该不等式组的整数解为2,3.
2
3
1
0
4
所以这个不等式组的解集是
解一元一次不等式组,在找“公共部分”的过程中,可借助数轴或口诀确定不等式组的解集.
4. 若不等式 的解集为-1解: 解不等式组得m+n因为不等式组的解集为-1解得 m=1,n=-2,
所以(m+n)2017=(-1)2023=-1
[思想方法] 根据题意可以把一元一次不等式(组)转化为方程(组)或把方程(组)转化为一元一次不等式(组),从而得解.
5. 某单位急需用车,但又不准备买车,他们准备和一个个体车主或一国营出租车公司签订月租车合同.设汽车每月行驶x km,应付给个体车主的月费用为y1元,应付给国营出租车公司的月费用为y2元,y1,y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题:
(1)每月行驶的路程在什么范围内时,租国营出租车公司的车合算
(2)每月行驶的路程等于多少时,租两家车的费用相同
(3)如果这个单位估计每月行驶的路程为2300 km,那么这个单位租哪家车合算
解:由图象可知:
(1)每月行驶的路程小于1500 km 时,租国营出租车公司的车合算.
(2)当每月行驶的路程为1500 km时,租两家车的费用相同.
(3)如果每月行驶的路程为2300 km,那么这个单位租个体车主的车合算.
6. 某公司为了扩大经营,决定购进6台机器用于生产某种活塞,现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示,经过预算,本次购买机器所耗资金不能超过34万元,则按该公司的要求可以有几种购买方案
解:设购买甲种机器x台,则购买乙种机器(6-x)台.根据题意得
7x+5(6-x)≤34,解得x≤2.
由题意知x是整数,且x≥0,所以x可取0,1,2.
故该公司按要求可以有三种购买方案,即:
方案一:不购买甲种机器,购买乙种机器6台;
方案二:购买甲种机器1台,购买乙种机器5台;
方案三:购买甲种机器2台,购买乙种机器4台.
解析:本题主要考查对不等式知识的应用能力.解决本题的关键是理解题中的条件和要求,并做出符合题意的解答.
甲 乙
价格(万元/台) 7 5
每台日产量(个) 100 60
解不等式的应用问题的步骤包括审、设、列、解、找、答这几个环节,而在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.
7. 暑假期间,两名家长计划带领若干名学生去旅游,他们联系了报价均为每人500元的两家旅行社,经协商,甲旅行社的优惠条件是:两名家长全额收费,学生都按七折收费;乙旅行社的优惠条件是家长、学生都按八折收费.假设这两位家长带领x名学生去旅游,他们应该选择哪家旅行社?
解:设选择甲旅行社所需费用为y1元,选择乙旅行社所需费用为y2元,则
y1=500×2+70%×500x=350x+1000
y2=80%×500(x+2)=400(x+2)=400x+800
当y1 = y2时,350x+1000=400x+800 , 解得x=4;
当y1>y2时,350x+1000>400x+800 , 解得x<4;
当y1<y2时,350x+1000<400x+800 , 解得x>4.
所以,当学生人数为4人时,甲、乙两家旅行社的收费相同;
当学生人数少于4人时,选择乙旅行社;
当学生人数多于4人时,选择甲旅行社.
章末复习题
第二章
《一元一次不等式与一元一次不等式组》
小结与复习
素养目标
技能目标
知识目标
了解一元一次不等式和一元一次不等式组的基本概念,了解不等式(组)的解和解集的概念。并会在数轴上表示其解集。
通过具体实际问题的解决,让学生初步体会不等式、方程、函数之间的内在联系与区别,加深对数学模型的认识。
通过小结与复习,培养学生归纳、整理所学知识的能力,从而激发学生的学习兴趣。
教学重点
教学难点
一元一次不等式基本性质的掌握及一元一次不等式(组)的解法,会在数轴上表示解集,能解决与不等式相关的实际问题。
从实际问题中抽象出数学模型及建立相关的知识体系。
基本性质
方程
等式
一次函数、正比例函数
函数
知识梳理
基本性质
一元一次不等式(组)
不等式
解决实际问题
一元一次方程
二元一次方程组
相互联系
一、不等式的有关概念
一般地,用不等号“>”(或“≥”),“<”(或“≤”),“≠”连接的式子叫做不等式。
种类 符号 实际意义 读法
小于号
大于号
小于或等于号
大于或等于号
不等号
<
小于,不足
小于
>
大于,高出
大于
≤
不大于,不超过
小于或等于
≥
不小于,至少
大于或等于
≠
不相等
不等于
比较不等式与等式的基本性质:
变 形 等 式 不等式
两边都加上(或减去)同一个整式
两边都乘以(或除以)同一个正数
两边都乘以(或除以)同一个负数
仍成立
仍成立
仍成立
仍成立
仍成立
?
不等号的方向改变才成立哦。
不等式还具有传递性:如果a > b,b > c,那么a > c.
一个含有未知数的不等式的所有解,组成这个不等式的解集.
比较不等式的解与不等式的解集:
区别 不等式的解 不等式的解集
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
①左右两边都是整式;
②只有一个未知数,且未知数的最高次数是1;
③用不等号连接的式子.
一元一次不等式的特征:
一元一次不等式的定义:不等式的左右两边都是整式,只含一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
解一元一次方程的步骤是什么
类似的,解一元一次不等式的步骤和解一元一次方程一样。在运用性质3时要特别注意:改变不等号的方向.
解一元一次方程的步骤:
①去分母;
②去括号;
③移项;
④合并同类项;
⑤系数化为1.
用数轴表示不等式解集的方法:
(1)画数轴;
(2)定边界点:若这个点包含于解集之中,则用实心点表示;不包含在解集中,则用空心点表示.
(3)定方向:相对于边界点,大于向右画,小于向左画.
用一元一次不等式解决实际问题的一般步骤:
(1)审:认真审题找出不等关系;
(2)设:设出适当未知数;
(3)列:根据题中的不等关系,列出不等式;
(4)解:解所列的不等式;
(5)答:根据实际情况写出答案.
在应用一元一次不等式解决实际问题时,要抓住题中的关键词,如“大于”“不大于”“至少”“不超过”等.
一元一次不等式与一次函数在决策型应用题中的应用
实际问题
写出两个函数表达式
列不等式
解不等式
画出图象
分析图象
解决问题
图象法
代数法
解决问题
要选择合理、简捷的方法解题。
一元一次不等式与一次函数在决策型应用题中的应用
利用图象法解不等式步骤:
(1)作出不等式左、右两边所对应的两个一次函数的图象.
(2)确定两个一次函数图象的交点坐标.
(3)找出哪段函数图象在上方,哪段函数在下方,从而确定自变量的取值范围.
一元一次不等式与一次函数在决策型应用题中的应用
刻画运动变化的规律需要用函数模型;
刻画变化过程中同类量之间的大小,需要用不等式模型;
刻画运动变化过程中的某一瞬间需要用方程模型。
解决实际问题时,要合理选择这三种数学模型.
确定一个不等式组是一元一次不等式需要满足三点:
(1)不等式组中只有一个未知数;
(2)未知数的最高次数是1;
(3)组成不等式的代数式都是整式.
在数轴上表示 解 集 口 诀
a
b
x > b
a
b
x < a
a
b
a < x < b
a
b
无解
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
同大取大
同小取小
大小小大中间找
大大小小无处找
1. 下列命题正确的是 ( )
A.若a>b,b
C.若a>b,则ac2>bc2 D.若ac2>bc2,则a>b
D
解析:
选项A,由a>b,b
选项B,a>b,当c=0时,ac=bc,不能根据不等式的性质确定ac>bc ;
选项C,a>b,当c=0时,ac2=bc2,不能根据不等式的性质确定ac2>bc2;
选项D,ac2>bc2,隐含c≠0 ,可以根据不等式的性质在不等式的两边同时除以正数c2,从而确定a>b.
2. 解不等式 并把解集在数轴上表示出来.
解: 去分母,得3(x-1) ≤ 1+x,
整理,得2x ≤ 4,
∴ x ≤ 2.
解集在数轴上表示如下图
2
1
-1
0
[思想方法] 明确不等式的解与解集的区别,用数轴表示不等式的解集时,要注意两点:一是分界点,二是方向.
3 . 解不等式组 把解集在数轴上表示出来,并将解集中的整数解写出来.
解:解不等式 ,得 x≤3,
解不等式 ,得
解集在数轴上表示如下:
通过观察数轴可知该不等式组的整数解为2,3.
2
3
1
0
4
所以这个不等式组的解集是
解一元一次不等式组,在找“公共部分”的过程中,可借助数轴或口诀确定不等式组的解集.
4. 若不等式 的解集为-1
所以(m+n)2017=(-1)2023=-1
[思想方法] 根据题意可以把一元一次不等式(组)转化为方程(组)或把方程(组)转化为一元一次不等式(组),从而得解.
5. 某单位急需用车,但又不准备买车,他们准备和一个个体车主或一国营出租车公司签订月租车合同.设汽车每月行驶x km,应付给个体车主的月费用为y1元,应付给国营出租车公司的月费用为y2元,y1,y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题:
(1)每月行驶的路程在什么范围内时,租国营出租车公司的车合算
(2)每月行驶的路程等于多少时,租两家车的费用相同
(3)如果这个单位估计每月行驶的路程为2300 km,那么这个单位租哪家车合算
解:由图象可知:
(1)每月行驶的路程小于1500 km 时,租国营出租车公司的车合算.
(2)当每月行驶的路程为1500 km时,租两家车的费用相同.
(3)如果每月行驶的路程为2300 km,那么这个单位租个体车主的车合算.
6. 某公司为了扩大经营,决定购进6台机器用于生产某种活塞,现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示,经过预算,本次购买机器所耗资金不能超过34万元,则按该公司的要求可以有几种购买方案
解:设购买甲种机器x台,则购买乙种机器(6-x)台.根据题意得
7x+5(6-x)≤34,解得x≤2.
由题意知x是整数,且x≥0,所以x可取0,1,2.
故该公司按要求可以有三种购买方案,即:
方案一:不购买甲种机器,购买乙种机器6台;
方案二:购买甲种机器1台,购买乙种机器5台;
方案三:购买甲种机器2台,购买乙种机器4台.
解析:本题主要考查对不等式知识的应用能力.解决本题的关键是理解题中的条件和要求,并做出符合题意的解答.
甲 乙
价格(万元/台) 7 5
每台日产量(个) 100 60
解不等式的应用问题的步骤包括审、设、列、解、找、答这几个环节,而在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.
7. 暑假期间,两名家长计划带领若干名学生去旅游,他们联系了报价均为每人500元的两家旅行社,经协商,甲旅行社的优惠条件是:两名家长全额收费,学生都按七折收费;乙旅行社的优惠条件是家长、学生都按八折收费.假设这两位家长带领x名学生去旅游,他们应该选择哪家旅行社?
解:设选择甲旅行社所需费用为y1元,选择乙旅行社所需费用为y2元,则
y1=500×2+70%×500x=350x+1000
y2=80%×500(x+2)=400(x+2)=400x+800
当y1 = y2时,350x+1000=400x+800 , 解得x=4;
当y1>y2时,350x+1000>400x+800 , 解得x<4;
当y1<y2时,350x+1000<400x+800 , 解得x>4.
所以,当学生人数为4人时,甲、乙两家旅行社的收费相同;
当学生人数少于4人时,选择乙旅行社;
当学生人数多于4人时,选择甲旅行社.
章末复习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
