1.3线段的垂直平分线(第2课时)同步课件(共21张PPT)
文档属性
| 名称 | 1.3线段的垂直平分线(第2课时)同步课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:49:05 | ||
图片预览



文档简介
(共21张PPT)
1.3 线段的垂直平分线
(第2课时)
素养目标
技能目标
知识目标
经历折纸和作图、猜想、证明的过程,能够证明三角形三边垂直平分线交于一点。
经历猜想-探索-能够作出以 a为底,h为高的等腰三角形。
体验解决问题的多样性发展推理能力和创新精神。锻炼克服困难的意志,建立自信心。
学习目标
教学重点
教学难点
能够证明与线段垂直平分线相关的结论。
已知底边和底边上的高,能够利用尺规作图作出等腰三角形。
证明三线共点
教学重难点
思考1: 拿出你们准备好的锐角三角形纸片,把三条边分别对折,观察三条折痕,你发现了什么?
思考2:作三角形三条边的垂直平分线,你发现了什么?
P
三条边的垂直平分线交于一点P
三条边的折痕交于一点
情境导入
例1 求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
P
A
B
C
已知:如图,在△ABC 中,边 AB 的垂直平分线与边 BC 的垂直平分线相交于点 P.
求证:边 AC 的垂直平分线经过点 P,且 PA=PB=PC.
分析:要想证明三条直线相交于一点,只要证明其中两条的交点在另一条直线上即可。我们联想到线段垂直平分线的性质定理和判定定理。
证明:∵点 P 在线段 AB 的垂直平分线上,
∴ PA = PB(线段垂直平分线上的点到这条线段两个端点的距离相等).
同理,PB = PC.
∴PA = PB = PC.
∴ 点 P 在线段 AC 的垂直平分线上(到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上),即边 AC 的垂直平分线经过点 P.
典例探究
数学符号语言如下:
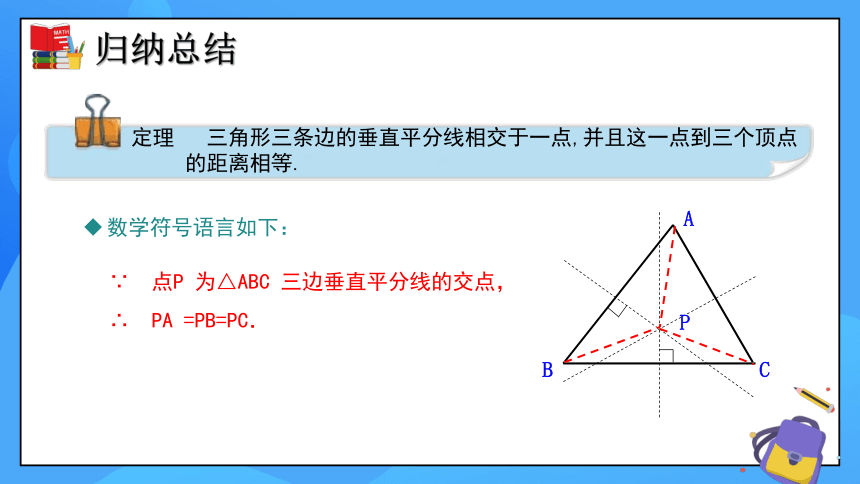
定理 三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点
的距离相等.
∵ 点P 为△ABC 三边垂直平分线的交点,
∴ PA =PB=PC.
A
B
C
P
归纳总结
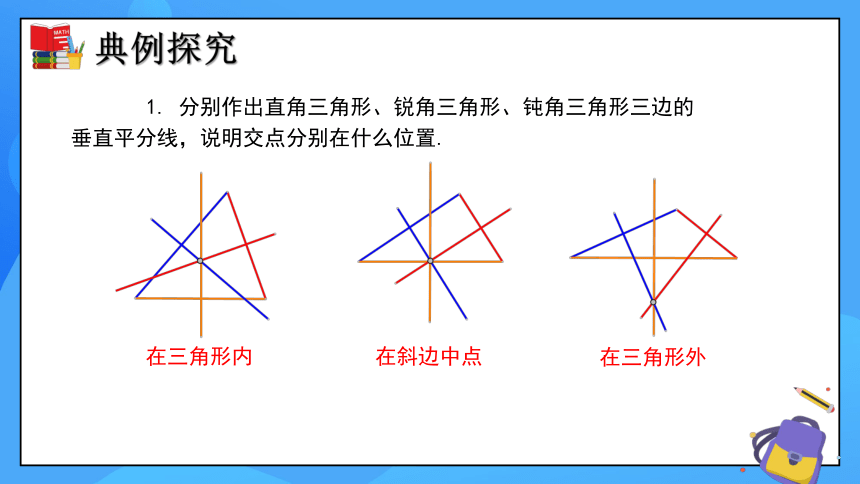
1. 分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
在三角形内
在斜边中点
在三角形外
典例探究
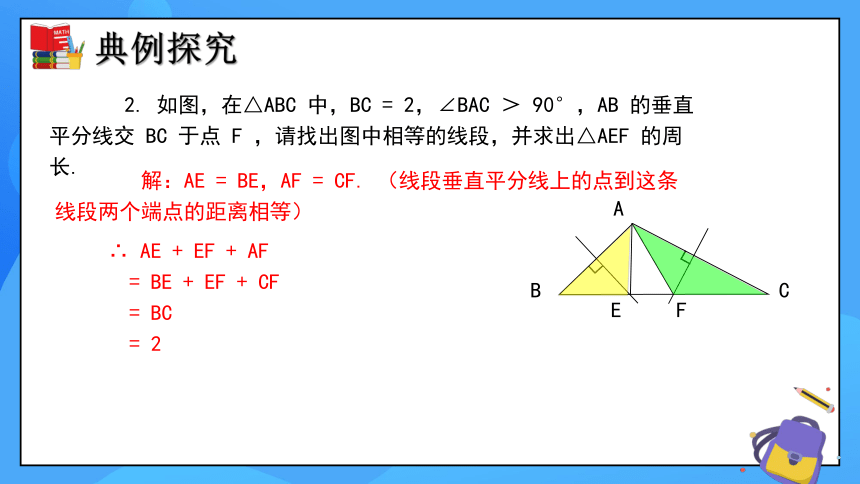
2. 如图,在△ABC 中,BC = 2,∠BAC > 90°,AB 的垂直平分线交 BC 于点 F ,请找出图中相等的线段,并求出△AEF 的周长.
A
B
C
E
F
解:AE = BE,AF = CF. (线段垂直平分线上的点到这条线段两个端点的距离相等)
∴ AE + EF + AF
= BE + EF + CF
= BC
= 2
典例探究
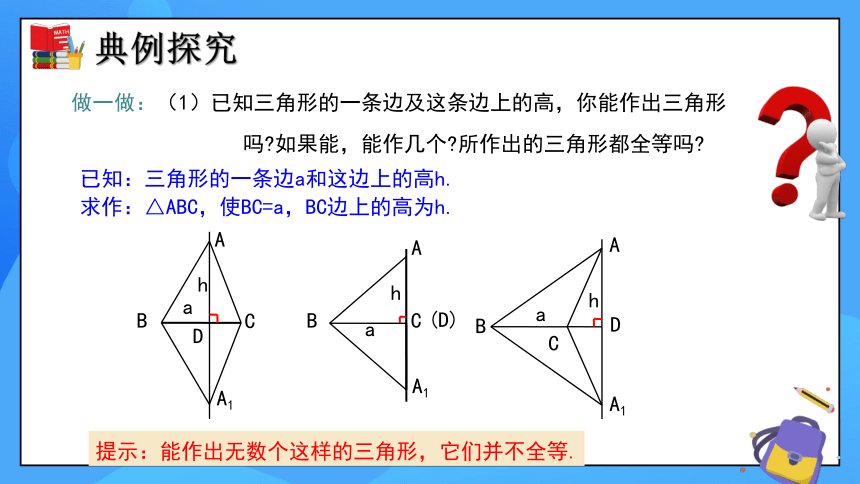
做一做:(1)已知三角形的一条边及这条边上的高,你能作出三角形
吗 如果能,能作几个 所作出的三角形都全等吗
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使BC=a,BC边上的高为h.
A1
D
C
B
A
a
h
(D)
C
B
A
a
h
A1
D
C
B
A
a
h
A1
提示:能作出无数个这样的三角形,它们并不全等.
典例探究
(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能画出几个?所画出的三角形都全等吗?
可以画出无数个三角形
典例探究
(3)已知等腰三角形的底边及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形应该只有两个,并且它们是全等的,分别位于已知底边的两侧.
典例探究
数学符号语言如下:
定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.线段垂直平分线上的点到这条线段两个端点的距离相等.
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
归纳总结
例 2 已知一个等腰三角形的底边及底边上的高,求作这个等腰三角形.
已知:如图,线段 a,h.
求作:△ABC,使 AB = AC,且 BC = a,高 AD = h.
a
h
作法:
(1)作线段 BC = a.
(2)作线段 BC 的垂直平分线 l,交 BC 于点 D.
(3)在 l 上作线段 DA,使 DA = h.
(4)连接 AB,AC.
△ABC为所求的等腰三角形.
B
C
A
a
h
D
典例探究
1.已知直线 l 和其上一点P,利用尺规作 l 的垂线,使它经过点P.
A
B
●
P
已知:直线 l 和 l 上一点P.
求作:PC⊥ l .
作法:
1.以点P为圆心,以任意长为半径作弧,
与直线 l 相交于点A和B.
2.作线段AB的垂直平分线PC.
直线PC就是所求 l 的垂线.
l
C
分为两种情况:第1种情况是点P在直线上;第2种情况是点P在直线外。
巩固训练
作法:
2.已知直线 l 和线外一点P,利用尺规作 l 的垂线,使它经过点P.
(1)先以P为圆心,大于点P到直线 l 的垂直距离R为半径作圆,交直线 l 于A,B.
(2)分别以A、B为圆心,大于R的长为半径作圆,相交于C、D两点.
(3)过两交点作直线 l ,此直线l为过点P的垂线.
巩固训练
定理
定理: 三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
尺规作图
已知等腰三角形的底边和底边上的高作等腰三角形.
思想方法
分类讨论,逆向思维.
文字语言-符号语言-图形语言的互相转化.
推理证明的重要性.
内容
归纳总结
1. 如图,在△ABC 中,已知 AC = 27,AB 的垂直平分线交 AB 于点 D,交 AC 于点 E,△BCE 的周长等于 50,求 BC 的长.
A
B
E
D
C
解:因为 DE 为 AB 的垂直平分线,
所以 AE = BE.
△BCE的周长为
d = EC + BE + BC
= EC + AE + BC
= AC + BC
= 27 + BC
= 50.
所以 BC = 23 .
巩固训练
2.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
A.80° B.70° C.60° D.50°
C
B
A
D
E
C
巩固训练
3. 如图,已知线段 a,求作以 a 为底边、以 a 为高的等腰三角形,这个等腰三角形有什么特征?
1
2
A
B
P
a
a
1
2
这是个等腰直角三角形
巩固训练
习题1.8第3、4题
1.3 线段的垂直平分线
(第2课时)
素养目标
技能目标
知识目标
经历折纸和作图、猜想、证明的过程,能够证明三角形三边垂直平分线交于一点。
经历猜想-探索-能够作出以 a为底,h为高的等腰三角形。
体验解决问题的多样性发展推理能力和创新精神。锻炼克服困难的意志,建立自信心。
学习目标
教学重点
教学难点
能够证明与线段垂直平分线相关的结论。
已知底边和底边上的高,能够利用尺规作图作出等腰三角形。
证明三线共点
教学重难点
思考1: 拿出你们准备好的锐角三角形纸片,把三条边分别对折,观察三条折痕,你发现了什么?
思考2:作三角形三条边的垂直平分线,你发现了什么?
P
三条边的垂直平分线交于一点P
三条边的折痕交于一点
情境导入
例1 求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
P
A
B
C
已知:如图,在△ABC 中,边 AB 的垂直平分线与边 BC 的垂直平分线相交于点 P.
求证:边 AC 的垂直平分线经过点 P,且 PA=PB=PC.
分析:要想证明三条直线相交于一点,只要证明其中两条的交点在另一条直线上即可。我们联想到线段垂直平分线的性质定理和判定定理。
证明:∵点 P 在线段 AB 的垂直平分线上,
∴ PA = PB(线段垂直平分线上的点到这条线段两个端点的距离相等).
同理,PB = PC.
∴PA = PB = PC.
∴ 点 P 在线段 AC 的垂直平分线上(到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上),即边 AC 的垂直平分线经过点 P.
典例探究
数学符号语言如下:
定理 三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点
的距离相等.
∵ 点P 为△ABC 三边垂直平分线的交点,
∴ PA =PB=PC.
A
B
C
P
归纳总结
1. 分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
在三角形内
在斜边中点
在三角形外
典例探究
2. 如图,在△ABC 中,BC = 2,∠BAC > 90°,AB 的垂直平分线交 BC 于点 F ,请找出图中相等的线段,并求出△AEF 的周长.
A
B
C
E
F
解:AE = BE,AF = CF. (线段垂直平分线上的点到这条线段两个端点的距离相等)
∴ AE + EF + AF
= BE + EF + CF
= BC
= 2
典例探究
做一做:(1)已知三角形的一条边及这条边上的高,你能作出三角形
吗 如果能,能作几个 所作出的三角形都全等吗
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使BC=a,BC边上的高为h.
A1
D
C
B
A
a
h
(D)
C
B
A
a
h
A1
D
C
B
A
a
h
A1
提示:能作出无数个这样的三角形,它们并不全等.
典例探究
(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能画出几个?所画出的三角形都全等吗?
可以画出无数个三角形
典例探究
(3)已知等腰三角形的底边及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形应该只有两个,并且它们是全等的,分别位于已知底边的两侧.
典例探究
数学符号语言如下:
定理 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.线段垂直平分线上的点到这条线段两个端点的距离相等.
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
归纳总结
例 2 已知一个等腰三角形的底边及底边上的高,求作这个等腰三角形.
已知:如图,线段 a,h.
求作:△ABC,使 AB = AC,且 BC = a,高 AD = h.
a
h
作法:
(1)作线段 BC = a.
(2)作线段 BC 的垂直平分线 l,交 BC 于点 D.
(3)在 l 上作线段 DA,使 DA = h.
(4)连接 AB,AC.
△ABC为所求的等腰三角形.
B
C
A
a
h
D
典例探究
1.已知直线 l 和其上一点P,利用尺规作 l 的垂线,使它经过点P.
A
B
●
P
已知:直线 l 和 l 上一点P.
求作:PC⊥ l .
作法:
1.以点P为圆心,以任意长为半径作弧,
与直线 l 相交于点A和B.
2.作线段AB的垂直平分线PC.
直线PC就是所求 l 的垂线.
l
C
分为两种情况:第1种情况是点P在直线上;第2种情况是点P在直线外。
巩固训练
作法:
2.已知直线 l 和线外一点P,利用尺规作 l 的垂线,使它经过点P.
(1)先以P为圆心,大于点P到直线 l 的垂直距离R为半径作圆,交直线 l 于A,B.
(2)分别以A、B为圆心,大于R的长为半径作圆,相交于C、D两点.
(3)过两交点作直线 l ,此直线l为过点P的垂线.
巩固训练
定理
定理: 三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
尺规作图
已知等腰三角形的底边和底边上的高作等腰三角形.
思想方法
分类讨论,逆向思维.
文字语言-符号语言-图形语言的互相转化.
推理证明的重要性.
内容
归纳总结
1. 如图,在△ABC 中,已知 AC = 27,AB 的垂直平分线交 AB 于点 D,交 AC 于点 E,△BCE 的周长等于 50,求 BC 的长.
A
B
E
D
C
解:因为 DE 为 AB 的垂直平分线,
所以 AE = BE.
△BCE的周长为
d = EC + BE + BC
= EC + AE + BC
= AC + BC
= 27 + BC
= 50.
所以 BC = 23 .
巩固训练
2.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
A.80° B.70° C.60° D.50°
C
B
A
D
E
C
巩固训练
3. 如图,已知线段 a,求作以 a 为底边、以 a 为高的等腰三角形,这个等腰三角形有什么特征?
1
2
A
B
P
a
a
1
2
这是个等腰直角三角形
巩固训练
习题1.8第3、4题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
