2.2 不等式的基本性质 同步课件(共21张PPT)
文档属性
| 名称 | 2.2 不等式的基本性质 同步课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:47 | ||
图片预览







文档简介
(共21张PPT)
2.2 不等式的基本性质
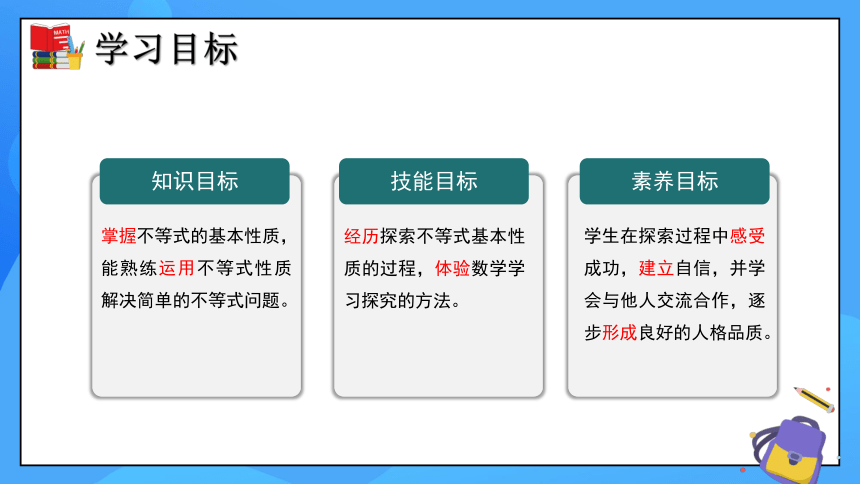
素养目标
技能目标
知识目标
掌握不等式的基本性质,能熟练运用不等式性质解决简单的不等式问题。
经历探索不等式基本性质的过程,体验数学学习探究的方法。
学生在探索过程中感受成功,建立自信,并学会与他人交流合作,逐步形成良好的人格品质。
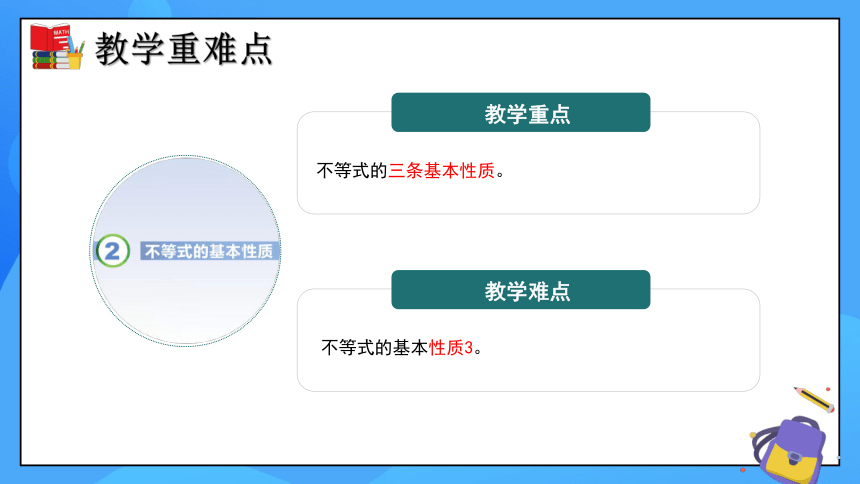
教学重点
教学难点
不等式的三条基本性质。
不等式的基本性质3。
思考1:
商场A种服装的价格为75元,B种服装的价格为90元
(1)两种服装都涨价10元,哪种服装价格高?涨价15元呢?
(2)两种服装都降价5元,哪种服装价格高?降价15元呢?
填空: 75 90
75+10 90+10
75+15 90+15
75 - 5 90 - 5
75-15 90-15
<
<
<
想一想:75+m 90+m
75 - n 90 - n
你发现了什么规律?你能用自己的话表达出来吗?
<
<
<
<
不等式的基本性质1
不等式的两边都加(或减)同一个整式,不等号的方向不变.
用字母表示为:
如果a > b,那么a + c > b + c,a – c > b - c.
如果a < b,那么a + c < b + c,a – c < b - c.
(1) x -7 < 8,
解:
不等式的两边都加上7,由不等式基本性质1,得
x -7+7 < 8+7,
即 x < 15 .
(1)x -7 < 8 ;
(2) 3x < 2x -3 .
(2) 3x < 2x -3,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,
即 x < -3.
例1 将下列不等式化成“x>a”“x<a”的形式.
思考2:
商场A种服装的价格为75元,B种服装的价格为90元
(3)两种服装都打8折出售,哪种服装价格高?
(4)两种服装都降半价出售,哪种服装价格高?
填空: 75 90
75×0.8 90×0.8
75÷2 90÷2
<
想一想:75×m 90×m (m>0)
75÷n 90÷n (n>0)
<
<
<
<
你发现了什么规律?你能用自己的话表达出来吗?
不等式的基本性质2
不等式的两边都乘(或除以)同一个正数,不等号的方向不变。
用字母表示为:
如果a > b,并且c > 0,那么ac > bc , .
如果a < b,并且c > 0,那么ac < bc , .
不等式的两边都加上3,由不等式基本性质1,得
不等式的两边都乘以2,由不等式基本性质2,得
例2 将下列不等式化成“x>a”“x<a”的形式.
解:
所以
即
3 –2,
3×(-6) (-2)×(-6) ,
3÷(-6) (-2) ÷(-6 )
思考3:
填空: 6 8
6×(-2) 8×(-2)
6÷(-2) 8÷(-2)
>
想一想:6×m 8×m (m<0)
6÷n 8÷n (n<0)
>
>
<
>
你发现了什么规律?你能用自己的话表达出来吗?
>
<
<
不等式的基本性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
用字母表示为:
如果a < b,并且c < 0,那么ac > bc , .
如果a > b,并且c < 0,那么ac < bc , .
不等式的两边都除以(-2),由不等式基本性质3,得
例3 将下列不等式化成“x>a”“x<a”的形式.
解:-2x> 3
-2x> 3
即
比较不等式与等式的基本性质:
变 形 等 式 不等式
两边都加上(或减去)同一个整式
两边都乘以(或除以)同一个正数
两边都乘以(或除以)同一个负数
仍成立
仍成立
仍成立
仍成立
仍成立
?
不等号的方向改变才成立哦。
问题1:
在上一节课中,我们猜想,无论绳长l取何值,圆的面积总大于正方形的面积,即
你相信这个结论吗?你能利用不等式的基本性质解释这一结论吗?
分母大的反而小
不等式的基本性质2,不等式的两边都乘以同一个正数,不等号的方向不变。
解:
问题2:
若x > y,则下列式子错误的是( ).
A. x-3 > y-3 B. -3x > -3y
C. x+3 > y+3 D.
B
问题3:
甲、乙两超市为了促销一种定价相同的商品,甲超市连续两次降价10%,乙超市一次降价20%,请问在哪家超市购买这种商品更合算
解:设这种商品的价格为a 元,
在甲超市购买需付款a(1-10%)(1-10%),即0.81a (元),
在乙超市购买需付款a(1-20%),即0.8a (元).
因为0.81>0.8,且a>0,
所以0.81a>0.8a.
故在乙超市购买这种商品更合算.
分析:分别用代数式表示出在两家超市购买商品的金额,然后利用不等式的基本性质比较两家消费金额的大小,从而确定在哪家超市购买这种商品更合算.
1.不等式的两边都加(或减)同一个整式,不等号的方向不变.
如果a>b,那么a+c>b+c,a-c>b-c
思想方法
逆向思维,转化思维,类比思维.
文字语言-符号语言互相转化.
数学建模.
不等式的基本性质
2.不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,且c>0, 那么
2.不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
如果a>b,且c<0,那么
1.小明做这样一题:已知2x>3x,求x的范围。结果小明两边同时除以x,得到2>3。你知道他错在哪
解:因为x是一个未知数,不知其是正数还是负数;如为负数,在两边除以x时,不等号方向应改变。正确做法为:
∵ 2x>3x
∴ 2x-3x>3x-3x
∴ -x>0
∴ -x×(-1)<0×(-1)
∴ x<0
2.某公司组织10辆汽车装运A,B两种苹果到外地销售,按规定每辆汽车只装同一种苹果,且必须装满.已知A,B两种苹果的每辆汽车的运载量及每吨获利如下表:
(1)若共运出苹果至少24吨,写出装运A种苹果的汽车辆数x应满足多少;
(2)若共获利不少于15 600元,写出装运A种苹果的汽车辆数x应满足多少.
分析:第(1)题中,装运B种苹果的汽车辆数为(10-x)辆,两种汽车的运载量分别为3x吨、2(10-x)吨,两种汽车的运载量的和至少(即“≥”)24吨;
第(2)题中,A种苹果所获的利润为500×3x元,B种苹果所获
的利润为900×2(10-x)元,利润的和不少于(即“≥”)15 600元.
解:(1)3x+2(10-x)≥24;
(2)500×3x+900×2(10-x)≥15 600.
上一节课中的一个例子
你能运用不等式的基本性质化简吗?
习题2.2第1、2、3题
2.2 不等式的基本性质
素养目标
技能目标
知识目标
掌握不等式的基本性质,能熟练运用不等式性质解决简单的不等式问题。
经历探索不等式基本性质的过程,体验数学学习探究的方法。
学生在探索过程中感受成功,建立自信,并学会与他人交流合作,逐步形成良好的人格品质。
教学重点
教学难点
不等式的三条基本性质。
不等式的基本性质3。
思考1:
商场A种服装的价格为75元,B种服装的价格为90元
(1)两种服装都涨价10元,哪种服装价格高?涨价15元呢?
(2)两种服装都降价5元,哪种服装价格高?降价15元呢?
填空: 75 90
75+10 90+10
75+15 90+15
75 - 5 90 - 5
75-15 90-15
<
<
<
想一想:75+m 90+m
75 - n 90 - n
你发现了什么规律?你能用自己的话表达出来吗?
<
<
<
<
不等式的基本性质1
不等式的两边都加(或减)同一个整式,不等号的方向不变.
用字母表示为:
如果a > b,那么a + c > b + c,a – c > b - c.
如果a < b,那么a + c < b + c,a – c < b - c.
(1) x -7 < 8,
解:
不等式的两边都加上7,由不等式基本性质1,得
x -7+7 < 8+7,
即 x < 15 .
(1)x -7 < 8 ;
(2) 3x < 2x -3 .
(2) 3x < 2x -3,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,
即 x < -3.
例1 将下列不等式化成“x>a”“x<a”的形式.
思考2:
商场A种服装的价格为75元,B种服装的价格为90元
(3)两种服装都打8折出售,哪种服装价格高?
(4)两种服装都降半价出售,哪种服装价格高?
填空: 75 90
75×0.8 90×0.8
75÷2 90÷2
<
想一想:75×m 90×m (m>0)
75÷n 90÷n (n>0)
<
<
<
<
你发现了什么规律?你能用自己的话表达出来吗?
不等式的基本性质2
不等式的两边都乘(或除以)同一个正数,不等号的方向不变。
用字母表示为:
如果a > b,并且c > 0,那么ac > bc , .
如果a < b,并且c > 0,那么ac < bc , .
不等式的两边都加上3,由不等式基本性质1,得
不等式的两边都乘以2,由不等式基本性质2,得
例2 将下列不等式化成“x>a”“x<a”的形式.
解:
所以
即
3 –2,
3×(-6) (-2)×(-6) ,
3÷(-6) (-2) ÷(-6 )
思考3:
填空: 6 8
6×(-2) 8×(-2)
6÷(-2) 8÷(-2)
>
想一想:6×m 8×m (m<0)
6÷n 8÷n (n<0)
>
>
<
>
你发现了什么规律?你能用自己的话表达出来吗?
>
<
<
不等式的基本性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
用字母表示为:
如果a < b,并且c < 0,那么ac > bc , .
如果a > b,并且c < 0,那么ac < bc , .
不等式的两边都除以(-2),由不等式基本性质3,得
例3 将下列不等式化成“x>a”“x<a”的形式.
解:-2x> 3
-2x> 3
即
比较不等式与等式的基本性质:
变 形 等 式 不等式
两边都加上(或减去)同一个整式
两边都乘以(或除以)同一个正数
两边都乘以(或除以)同一个负数
仍成立
仍成立
仍成立
仍成立
仍成立
?
不等号的方向改变才成立哦。
问题1:
在上一节课中,我们猜想,无论绳长l取何值,圆的面积总大于正方形的面积,即
你相信这个结论吗?你能利用不等式的基本性质解释这一结论吗?
分母大的反而小
不等式的基本性质2,不等式的两边都乘以同一个正数,不等号的方向不变。
解:
问题2:
若x > y,则下列式子错误的是( ).
A. x-3 > y-3 B. -3x > -3y
C. x+3 > y+3 D.
B
问题3:
甲、乙两超市为了促销一种定价相同的商品,甲超市连续两次降价10%,乙超市一次降价20%,请问在哪家超市购买这种商品更合算
解:设这种商品的价格为a 元,
在甲超市购买需付款a(1-10%)(1-10%),即0.81a (元),
在乙超市购买需付款a(1-20%),即0.8a (元).
因为0.81>0.8,且a>0,
所以0.81a>0.8a.
故在乙超市购买这种商品更合算.
分析:分别用代数式表示出在两家超市购买商品的金额,然后利用不等式的基本性质比较两家消费金额的大小,从而确定在哪家超市购买这种商品更合算.
1.不等式的两边都加(或减)同一个整式,不等号的方向不变.
如果a>b,那么a+c>b+c,a-c>b-c
思想方法
逆向思维,转化思维,类比思维.
文字语言-符号语言互相转化.
数学建模.
不等式的基本性质
2.不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,且c>0, 那么
2.不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
如果a>b,且c<0,那么
1.小明做这样一题:已知2x>3x,求x的范围。结果小明两边同时除以x,得到2>3。你知道他错在哪
解:因为x是一个未知数,不知其是正数还是负数;如为负数,在两边除以x时,不等号方向应改变。正确做法为:
∵ 2x>3x
∴ 2x-3x>3x-3x
∴ -x>0
∴ -x×(-1)<0×(-1)
∴ x<0
2.某公司组织10辆汽车装运A,B两种苹果到外地销售,按规定每辆汽车只装同一种苹果,且必须装满.已知A,B两种苹果的每辆汽车的运载量及每吨获利如下表:
(1)若共运出苹果至少24吨,写出装运A种苹果的汽车辆数x应满足多少;
(2)若共获利不少于15 600元,写出装运A种苹果的汽车辆数x应满足多少.
分析:第(1)题中,装运B种苹果的汽车辆数为(10-x)辆,两种汽车的运载量分别为3x吨、2(10-x)吨,两种汽车的运载量的和至少(即“≥”)24吨;
第(2)题中,A种苹果所获的利润为500×3x元,B种苹果所获
的利润为900×2(10-x)元,利润的和不少于(即“≥”)15 600元.
解:(1)3x+2(10-x)≥24;
(2)500×3x+900×2(10-x)≥15 600.
上一节课中的一个例子
你能运用不等式的基本性质化简吗?
习题2.2第1、2、3题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
