15.2.3 整数指数幂 课件 2023—-2024学年人教版数学八年级上册(25张PPT)
文档属性
| 名称 | 15.2.3 整数指数幂 课件 2023—-2024学年人教版数学八年级上册(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 332.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 08:34:28 | ||
图片预览


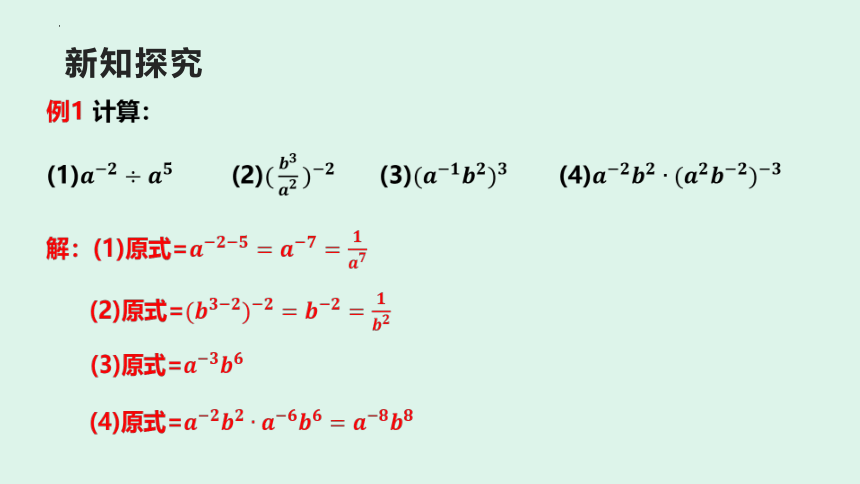



文档简介
(共25张PPT)
15.2.3整数指数幂(第1课时)
人教版 八年级上册
新知探究
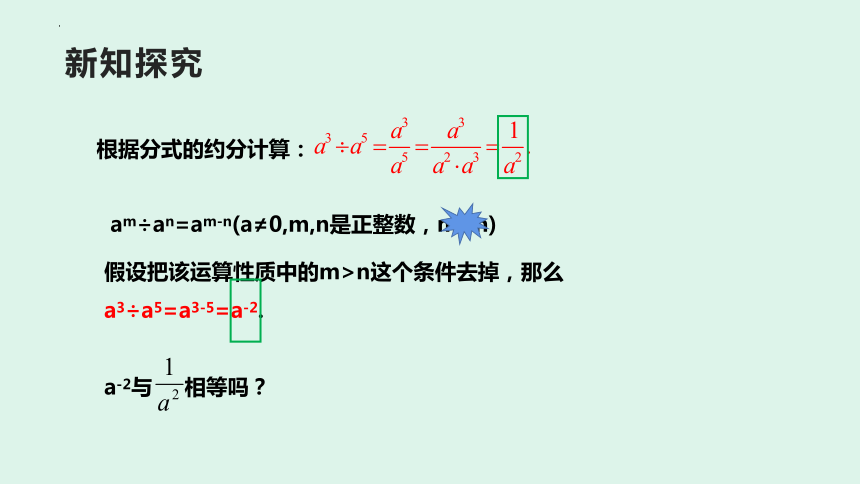
根据分式的约分计算:
am÷an=am-n(a≠0,m,n是正整数,m>n)
假设把该运算性质中的m>n这个条件去掉,那么a3÷a5=a3-5=a-2.
a-2与 相等吗?
新知探究
am·an=am + n这条性质对于m,n是任意整数的情形仍然适用.
事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂.
(1) am·an=am+n
(2) (am)n=amn
(3) ( ab) n =a n b n
(4) am÷an=am – n
(a≠0 ,m>n)
(5)
(6) a0=1
(a≠0)
(m,n是整数)
(a≠0)
整数指数幂运算性质
新知探究
例1 计算:
(1) (2) (3) (4)
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
新知探究
(1) 根据整数指数幂的运算性质,
当m,n为整数时,am ÷an=am-n
又am ·a-n=am-n
即同底数幂的除法可以转化为同底数幂的乘法.
即商的乘方可以转化为积的乘方.
因此am ÷an=am ·a-n.
(2) 特别地, ,所以
课堂练习
1.2-3可以表示为( )
A.22÷25 B.25÷22
C.22×25 D.(-2)×(-2)×(-2)
A
2.(-2)-2等于( )
A.-4 B.4 C. D.
D
课堂练习
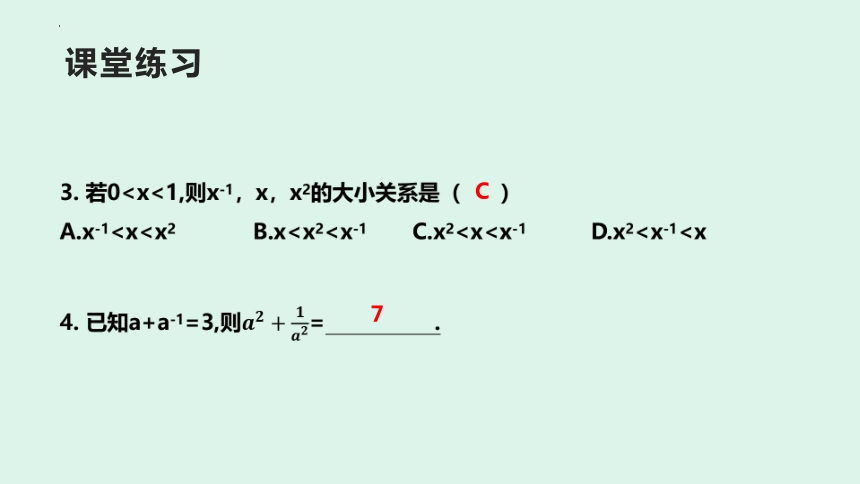
3. 若0A.x-14. 已知a+a-1=3,则= .
C
7
课堂练习
5.若3n= ,则n= .
6.若4﹣3×4﹣1×40=4p,则p的值为 .
-3
-4
回顾复习
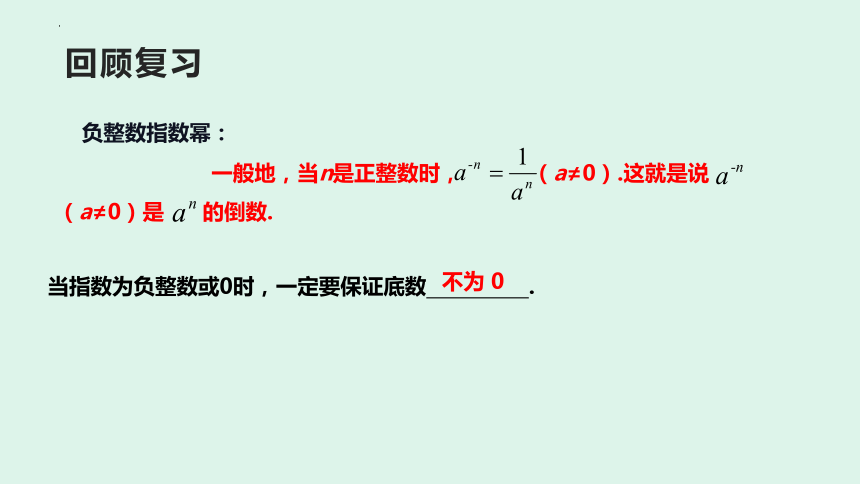
负整数指数幂:
当指数为负整数或0时,一定要保证底数 .
不为 0
一般地,当n是正整数时, (a≠0).这就是说 (a≠0)是 的倒数.
新知探究
我们已经知道,一些较大的数适合用科学记数法表示,例如光速约为3×108m/s,太阳的半径约为6.96×105km等.
那么,类似0.00001、0.0000257、 0.0000000257这样的数能不能也用科学记数法表示?
新知探究
根据负整数指数幂有
0.00001
0.0000257
0.0000000257
你能归纳出用科学记数法表示小于1的正数的方法吗?
新知探究
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值小于1的数,即将它们表示成a×10-n的形式. (其中n是正整数,1≤∣a∣<10.)
n
新知探究
观察小数点后至第一个非0数字前0的个数与指数关系.
0.1=
0.001 =
0.01 =
0.000 1 =
0.000 000 001 =
…
8个0
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
新知探究
对于一个小于1的正小数,如果小数点后至第一个非0数字前有m个0,用科学记数法表示这个数时,10的指数
– (m+1).
新知探究
例1 用科学记数法表示下列各数.
(1)0.000 04; (2)-0.034;
(3)0.000 000 45.
分析:数清每个数中左起第一个非0的数字前面有
几个0,用科学记数法表示时10的指数就是
负几.
解: (1)0.000 04=4×10-5;
(2)-0.034=-3.4×10-2;
(3)0.000 000 45=4.5×10-7.
新知探究
用科学记数法表示小于1的正数的一般步骤:
(1) 确定a:a是大于或等于1且小于10的数;
(2) 确定n:小数点后至第一个非0数字前,0的个数加1为n.
将原数用科学记数法表示为a×10–n(其中1≤a<10,n是正整数).
新知探究
注意事项
(1)对于大于-1的负数也可以类似地用科学记数法表示,即绝对值小于1的数都可以用科学记数法表示成a×10-n的形式(其中1≤∣a∣<10,n是正整数);(2)用科学记数法表示绝对值小于1的数时,10的指数是负数,一定不要忘记指数n前面的“-”号;(3)用科学记数法表示一个负数时,不要忘了前面带“-”号,用科学记数法表示一个带有单位的数时,其表示结果也应带有单位.
新知探究
例2 纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓球上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个1nm3的物体(物体之间隙忽略不计)?
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
新知探究
把用科学记数法表示的数还原成原数时,指数n表示第一个有效数字前0的个数。
课堂练习
1.用科学计数法表示下列数:
0.000 000 001,0.001 2,
0.000 000 345, 0.000 000 010 8.
2.用科学记数法表示0.000031,结果是( )
A.3.1×10-4 B.3.1×10-5
C.0.31×104 D.3.1×104
解:(1) 10-9 ; (2) 1.2×10-3 ; (3) 3.45×10-7 ;
(4) 1.08×10-3 .
B
课堂练习
3.截至2022年6月1日,北京市已建成34个地下调蓄设施,蓄水能力达到140000立方米.将140000用科学记数法表示应为( )
A.14×104 B.1.4×105
C.1.4×106 D.0.14×106
B
课堂练习
5.我国北斗公司在2022年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了 米,用科学记数法表示 为( )
A.2×10﹣5 B.2×10﹣6 C.5×10﹣5 D.5×10﹣6
4.若 用科学记数法表示为1.8×10﹣10,则n的值是( )
A.9 B.10 C.11 D.12
A
D
课堂练习
6.用小数表示下列各数.
(1)6×10-6= ;
(2)3.14×10-3= ;
(3)1.8×10-8= ;
(4)5.07×10-1= .
0.000006
0.00314
0.000000018
0.507
7.比较大小:
(1)3.01×10-4_______9.5×10-3
(2)3.01×10-4_______3.10×10-4
<
<
课堂练习
8.一个900 mm2的芯片上能集成10亿个元件.
(1)每个这样的元件约占多少平方毫米?
(2)每个这样的元件约占多少平方米?(用科学记数法表示)
解:(1)10亿=10×108=109,
∴900÷109=9×10-7(mm2).
答:每个这样的元件约占9×10-7 mm2;
(2)1 m2=106 mm2,
∴9×10-7÷106=9×10-13(m2).
答:每个这样的元件约占9×10-13 m2.
课堂小结
整数指数幂
负整数指数幂
零指数幂
当a≠0时,a0=1.
整数指数幂
一般地,当n是正整数时, (a≠0).
这就是说a-n(a≠0)是an 的倒数.
整数指数幂的运算性质可以归结为:
(1)am·an=am+n(m,n都是整数);
(2)(am)n=amn(m,n都是整数);
(3)(ab)n=anbn(n是整数).
15.2.3整数指数幂(第1课时)
人教版 八年级上册
新知探究
根据分式的约分计算:
am÷an=am-n(a≠0,m,n是正整数,m>n)
假设把该运算性质中的m>n这个条件去掉,那么a3÷a5=a3-5=a-2.
a-2与 相等吗?
新知探究
am·an=am + n这条性质对于m,n是任意整数的情形仍然适用.
事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂.
(1) am·an=am+n
(2) (am)n=amn
(3) ( ab) n =a n b n
(4) am÷an=am – n
(a≠0 ,m>n)
(5)
(6) a0=1
(a≠0)
(m,n是整数)
(a≠0)
整数指数幂运算性质
新知探究
例1 计算:
(1) (2) (3) (4)
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
新知探究
(1) 根据整数指数幂的运算性质,
当m,n为整数时,am ÷an=am-n
又am ·a-n=am-n
即同底数幂的除法可以转化为同底数幂的乘法.
即商的乘方可以转化为积的乘方.
因此am ÷an=am ·a-n.
(2) 特别地, ,所以
课堂练习
1.2-3可以表示为( )
A.22÷25 B.25÷22
C.22×25 D.(-2)×(-2)×(-2)
A
2.(-2)-2等于( )
A.-4 B.4 C. D.
D
课堂练习
3. 若0
C
7
课堂练习
5.若3n= ,则n= .
6.若4﹣3×4﹣1×40=4p,则p的值为 .
-3
-4
回顾复习
负整数指数幂:
当指数为负整数或0时,一定要保证底数 .
不为 0
一般地,当n是正整数时, (a≠0).这就是说 (a≠0)是 的倒数.
新知探究
我们已经知道,一些较大的数适合用科学记数法表示,例如光速约为3×108m/s,太阳的半径约为6.96×105km等.
那么,类似0.00001、0.0000257、 0.0000000257这样的数能不能也用科学记数法表示?
新知探究
根据负整数指数幂有
0.00001
0.0000257
0.0000000257
你能归纳出用科学记数法表示小于1的正数的方法吗?
新知探究
类似地,我们可以利用10的负整数次幂,用科学记数法表示一些绝对值小于1的数,即将它们表示成a×10-n的形式. (其中n是正整数,1≤∣a∣<10.)
n
新知探究
观察小数点后至第一个非0数字前0的个数与指数关系.
0.1=
0.001 =
0.01 =
0.000 1 =
0.000 000 001 =
…
8个0
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
新知探究
对于一个小于1的正小数,如果小数点后至第一个非0数字前有m个0,用科学记数法表示这个数时,10的指数
– (m+1).
新知探究
例1 用科学记数法表示下列各数.
(1)0.000 04; (2)-0.034;
(3)0.000 000 45.
分析:数清每个数中左起第一个非0的数字前面有
几个0,用科学记数法表示时10的指数就是
负几.
解: (1)0.000 04=4×10-5;
(2)-0.034=-3.4×10-2;
(3)0.000 000 45=4.5×10-7.
新知探究
用科学记数法表示小于1的正数的一般步骤:
(1) 确定a:a是大于或等于1且小于10的数;
(2) 确定n:小数点后至第一个非0数字前,0的个数加1为n.
将原数用科学记数法表示为a×10–n(其中1≤a<10,n是正整数).
新知探究
注意事项
(1)对于大于-1的负数也可以类似地用科学记数法表示,即绝对值小于1的数都可以用科学记数法表示成a×10-n的形式(其中1≤∣a∣<10,n是正整数);(2)用科学记数法表示绝对值小于1的数时,10的指数是负数,一定不要忘记指数n前面的“-”号;(3)用科学记数法表示一个负数时,不要忘了前面带“-”号,用科学记数法表示一个带有单位的数时,其表示结果也应带有单位.
新知探究
例2 纳米是非常小的长度单位,1nm=10-9m.把1nm3的物体放到乒乓球上,就如同把乒乓球放到地球上,1mm3的空间可以放多少个1nm3的物体(物体之间隙忽略不计)?
答:1mm3的空间可以放1018个1nm3的物体.
解:
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
新知探究
把用科学记数法表示的数还原成原数时,指数n表示第一个有效数字前0的个数。
课堂练习
1.用科学计数法表示下列数:
0.000 000 001,0.001 2,
0.000 000 345, 0.000 000 010 8.
2.用科学记数法表示0.000031,结果是( )
A.3.1×10-4 B.3.1×10-5
C.0.31×104 D.3.1×104
解:(1) 10-9 ; (2) 1.2×10-3 ; (3) 3.45×10-7 ;
(4) 1.08×10-3 .
B
课堂练习
3.截至2022年6月1日,北京市已建成34个地下调蓄设施,蓄水能力达到140000立方米.将140000用科学记数法表示应为( )
A.14×104 B.1.4×105
C.1.4×106 D.0.14×106
B
课堂练习
5.我国北斗公司在2022年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了 米,用科学记数法表示 为( )
A.2×10﹣5 B.2×10﹣6 C.5×10﹣5 D.5×10﹣6
4.若 用科学记数法表示为1.8×10﹣10,则n的值是( )
A.9 B.10 C.11 D.12
A
D
课堂练习
6.用小数表示下列各数.
(1)6×10-6= ;
(2)3.14×10-3= ;
(3)1.8×10-8= ;
(4)5.07×10-1= .
0.000006
0.00314
0.000000018
0.507
7.比较大小:
(1)3.01×10-4_______9.5×10-3
(2)3.01×10-4_______3.10×10-4
<
<
课堂练习
8.一个900 mm2的芯片上能集成10亿个元件.
(1)每个这样的元件约占多少平方毫米?
(2)每个这样的元件约占多少平方米?(用科学记数法表示)
解:(1)10亿=10×108=109,
∴900÷109=9×10-7(mm2).
答:每个这样的元件约占9×10-7 mm2;
(2)1 m2=106 mm2,
∴9×10-7÷106=9×10-13(m2).
答:每个这样的元件约占9×10-13 m2.
课堂小结
整数指数幂
负整数指数幂
零指数幂
当a≠0时,a0=1.
整数指数幂
一般地,当n是正整数时, (a≠0).
这就是说a-n(a≠0)是an 的倒数.
整数指数幂的运算性质可以归结为:
(1)am·an=am+n(m,n都是整数);
(2)(am)n=amn(m,n都是整数);
(3)(ab)n=anbn(n是整数).
