2023-2024学年江苏省常州二十四中教育集团九年级(上)期中数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年江苏省常州二十四中教育集团九年级(上)期中数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 380.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 21:48:27 | ||
图片预览




文档简介
2023-2024学年江苏省常州二十四中教育集团九年级(上)期中数学试卷
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1.已知关于的一元二次方程的常数项是,则的值为
( )
A. B. C. 或 D.
2.在中,,,,以为圆心,为半径作,则点与的位置关系是
( )
A. 点在内 B. 点在上 C. 点在外 D. 无法确定
3.下列各组的四条线段,,,是成比例线段的是
( )
A. ,,,
B. ,,,
C. ,,,
D. ,,,
4.以下命题中,两个直角三角形一定相似;两个等边三角形一定相似;两个菱形一定相似;任意两个矩形一定相似;两个正六边形一定相似.其中真命题的个数是
( )
A. 个 B. 个 C. 个 D. 个
5.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点,,都在横线上.若线段,则线段的长是
( )
A. B. C. D.
6.如图,某建筑工程队在工地一边靠墙处,用米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为平方米.为了方便取物,在各个仓库之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则可列方程
( )
A. B.
C. D.
7.如图,的直径与弦的延长线交于点,若,,则等于
( )
A. B. C. D.
8.如图,矩形中,点在边上,,,,点是矩形内一动点,满足,连接绕点逆时针旋转至,连接,则的最小值为
( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
9.在比例尺是的地图上,若某条道路长约为,则它的实际长度约为 .
10.若,则 .
11.鹦鹉螺是一类古老的软体动物.鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例,是自然界最美的鬼斧神工.如图,是的黄金分割点,若线段的长为,则的长为 结果保留根号
12.如图,是的直径,点,在上.若,则 .
13.圆内接四边形中,;则的度数为 .
14.设,是方程的两根,则的值是 .
15.若是一元二次方程的一个解,则的值为 .
16.在中,,,点是的中点,点为上一动点,当 时,与相似.
17.如图,已知,,,,是轴上的点,且,分别过点,,,作轴的垂线交直线于点,,,,连接,,,,,,,依次相交于点,,,,,,,,的面积依次为,,,,则为 .
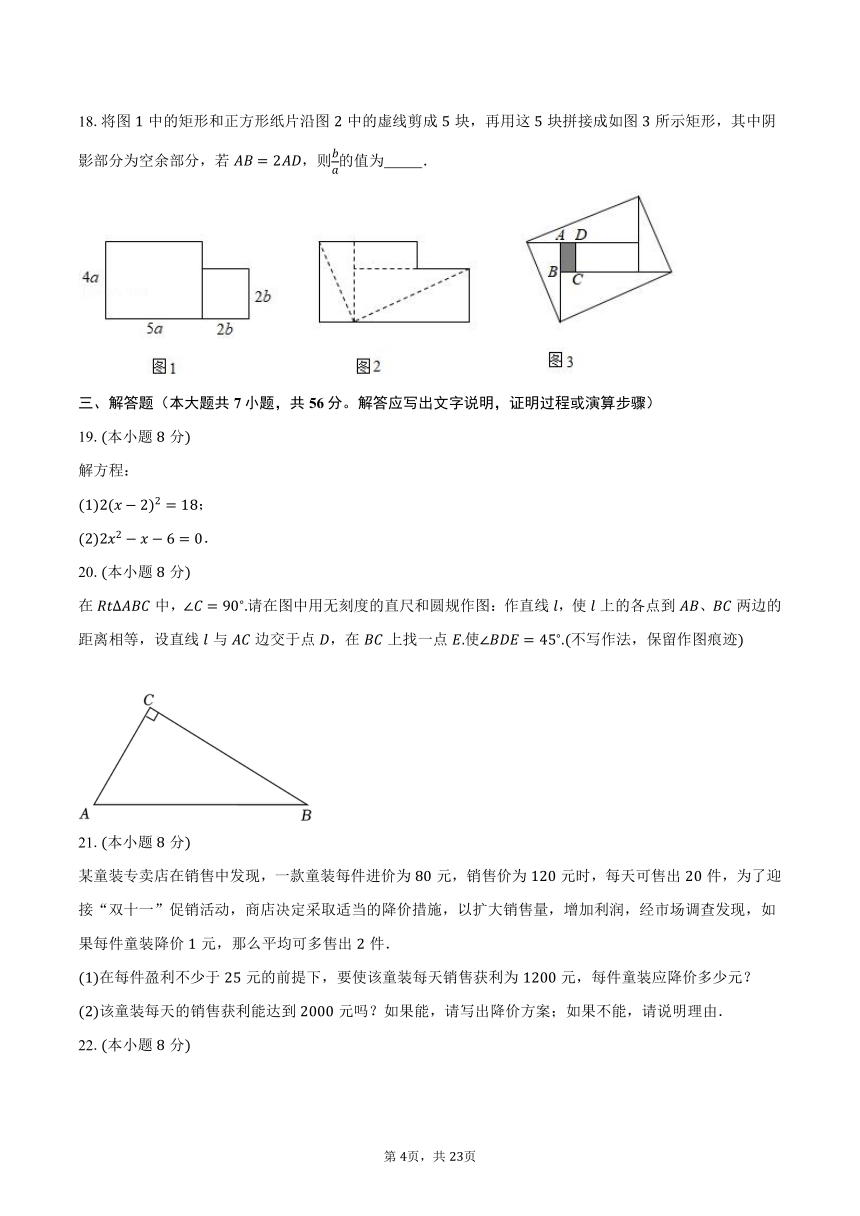
18.将图中的矩形和正方形纸片沿图中的虚线剪成块,再用这块拼接成如图所示矩形,其中阴影部分为空余部分,若,则的值为 .
三、解答题(本大题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤)
19.本小题分
解方程:
;
.
20.本小题分
在中,请在图中用无刻度的直尺和圆规作图:作直线,使上的各点到、两边的距离相等,设直线与边交于点,在上找一点使不写作法,保留作图痕迹
21.本小题分
某童装专卖店在销售中发现,一款童装每件进价为元,销售价为元时,每天可售出件,为了迎接“双十一”促销活动,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价元,那么平均可多售出件.
在每件盈利不少于元的前提下,要使该童装每天销售获利为元,每件童装应降价多少元?
该童装每天的销售获利能达到元吗?如果能,请写出降价方案;如果不能,请说明理由.
22.本小题分
如图,是的直径,点是劣弧中点,与相交于点连接,,与的延长线相交于点.
求证:是的切线;
求证:;
若,,请直接写出__.
23.本小题分
如图,四边形是证明勾股定理时用到的一个图形,,,是和边长,易知,这时我们把关于的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
判断下列方程是否是“勾系一元二次方程”:
__填“是”或“不是”;
__填“是”或“不是”
求证:关于的“勾系一元二次方程”必有实数根;
若是“勾系一元二次方程”的一个根,且四边形的周长是,求面积.
24.本小题分
综合与实践
动手操作:
如图,在中,,将绕点逆时针旋转得到延长分别交于点,交于点,连接.
思考探究:
__,__;
若,则
__;
__;
开放拓展:
如图,若改变旋转角,已知,,当时,请直接写出的面积为__.
25.本小题分
如图,在平面直角坐标系内,,为轴上两点,以为直径的交轴于,两点,为的中点,弦交轴于点,且点的坐标为,.
求的半径;
动点在的圆周上运动,连接,交于点.
如图,当平分时,求的值;
如图,过点作的切线交轴于点,当点与点,不重合时,是否为定值?若是,请求出其值;若不是,请说明理由.
答案和解析
1.【答案】
【解析】【分析】根据一元二次方程的定义和题意列出满足的条件求解即可.
【解答】解:由题意,
解得:,
故选:.
2.【答案】
【解析】【分析】利用勾股定理求得边的长,然后通过比较与半径的长即可得到结论.
【解答】解:中,,,,
,
,
点在内,
故选:.
3.【答案】
【解析】【分析】根据比例线段的定义,让最小的和最大的相乘,另外两个相乘,看它们的积是否相等,对选项一一分析,即可得出答案.
【解答】解:、,故此选项不符合题意;
、,故此选项不符合题意;
、,故此选项不符合题意;
、,故此选项符合题意,
故选:.
4.【答案】
【解析】【分析】根据相似图形的定义,形状相同的图形是相似图形.具体的说就是对应的角相等,对应边的比相等,对每个命题进行判断.
【解答】解:任意两个直角三角形,不能判断它们的对应角相等,对应边的比相等,所以不一定相似,故原命题为假命题;
任意两个等边三角形,它们的内角相等,对应边的比相等.所以一定相似,故原命题为真命题;
任意两个菱形,只能判断对应边的比相等,不能判断对应的角相等.所以不一定相似,故原命题为假命题;
任意两个矩形,它们的对应角相等,不能判断对应边的比相等.所以不一定相似,故原命题为假命题;
任意两个正六边形,它们的内角相等,对应边的比相等.所以一定相似,故原命题为真命题.
故选:.
5.【答案】
【解析】【分析】过点作平行横线的垂线,交点所在的平行横线于,交点所在的平行横线于,根据平行线分线段成比例定理列出比例式,计算即可.
【解答】详解:过点作平行横线的垂线,交点所在的平行横线于,交点所在的平行横线于,则,
即,
解得:,
.
故选:.
6.【答案】
【解析】【分析】根据铁栅栏的总长及的长,可得出米,根据仓库总面积为平方米,即可列出关于的一元二次方程,解之即可得出结论.
【解答】解:铁栅栏的总长为米,且米,
米,
根据题意得:.
故选:.
7.【答案】
【解析】【分析】利用,得到,则,根据三角形外角性质得,所以,同理得到,然后利用进行计算即可.
【解答】解:连接,如图,
,,
,
,
,
,
而,
,
,
,
.
故选:.
8.【答案】
【解析】【分析】取的中点,再把绕点逆时针旋转至,连接,,,则有,即可求出,然后过点作于点,连接,利用勾股定理可以得到,再根据求出结果.
【解答】解:如图,取的中点,再把绕点逆时针旋转至,连接,,,
,
,
根据旋转可得:,,
,,
,
,
,
,
点在以为圆心,为半径的圆上移动,
过点作于点,连接,
则四边形是矩形,
,,
,
,
,
故选:.
9.【答案】
【解析】【分析】根据比例尺图上距离:实际距离,依题意列比例式直接求解即可.
【解答】解:设它的实际长度约为,则
,
解得,
.
它的实际长度约为.
故答案为:.
10.【答案】
【解析】【分析】利用设法进行计算,即可解答.
【解答】解:设,
,,
,
故答案为:.
11.【答案】
【解析】【分析】根据黄金分割的定义进行计算,即可解答.
【解答】解:是的黄金分割点,,
,
,
故答案为:.
12.【答案】
【解析】【分析】根据圆周角定理得到,,然后利用互余计算出,从而得到的度数.
【解答】解:为的直径,
,
,
,
.
故答案为:.
13.【答案】
【解析】【分析】根据圆内接四边形对角互补求解.
【解答】解:四边形是圆内接四边形,
,
,
.
故答案为:.
14.【答案】
【解析】【分析】根据根与系数的关系,直接代入求解即可得到答案.
【解答】解:,是方程的两根,
,,
,
故答案为:.
15.【答案】
【解析】【分析】把代入方程中得:,从而可得,然后代入式子中进行计算,即可解答.
【解答】解:把代入方程中得:,
,
,
故答案为:.
16.【答案】或
【解析】【分析】根据相似三角形的性质可得比例关系进而得出的值.
【解答】解:和相似时,
或者,
在中,,,点是的中点,
,
,即,
解得,
,即,
解得.
故答案为:或.
17.【答案】
【解析】【分析】根据图象上点的坐标性质得出点、、、、、各点坐标,进而利用相似三角形的判定与性质得出、、、、,进而得出答案.
【解答】解:、、、、、是轴上的点,且,分别过点、、、、、作轴的垂线交直线于点、、、、、,
依题意得:,,,,
,
,
,
与对应高的比为:,
,
边上的高为,
,
同理可得:,,
.
故答案为:.
18.【答案】
【解析】【分析】如图,设,则,,首先证明,利用相似三角形的性质构建关系式,即可解决问题.
【解答】解:如图,设,则,,
,,
,
,
,
,
,
,,
,
,
,
,
整理得,,
,
,
,
.
故答案为:
19.【答案】解:由原方程,得
,
开方,得
,
解得,;
由原方程,得
,
解得,.
【解析】【分析】利用直接开平方法解方程即可;
利用“十字相乘法”对等式的左边进行因式分解,然后解方程.
20.【答案】解:作的平分线,交于点,则直线即为所求作的直;作线段的垂直平分线和以为直径的,与半圆的交点为,连接,与的交点即为点,如图:
【解析】【分析】作的平分线,交于点,则直线即为所求作的直;作线段的垂直平分线和以为直径的,与半圆的交点为,连接,与的交点即为点.
21.【答案】解:设每件童装降价元时,每天可销售件,每件盈利为元,
由题意得:,
整理得:,
解得:,,
当时,每件盈利为:,不合题意,舍去;
当时,每件盈利为:,符合题意;
答:每件童装应降价元;
不能,理由如下:
设童装每天的销售获利为元,
由知,,
当时,的值最大,最大值为,
该童装每天的销售获利不能达到元.
【解析】【分析】设每件童装降价元时,每天可销售件,每件盈利为元,根据总利润每件利润销售数量,列出一元二次方程,解方程并由每件盈利不少于元,即可得出答案;
设童装每天的销售获利为元,根据总利润每件利润销售数量,求最大值即可.
22.【答案】证明:连接交于点,则,
,
,
,
是的直径,
,
是的半径,且,
是的切线.
证明:点是劣弧中点,
,
,
,
,
,
.
解:,,
,
,
,
,,
,
,
,
,
,,
,
故答案为:.
【解析】【分析】连接交于点,由,,得,则,即可证明是的切线;
由点是劣弧中点,根据垂径定理得,则,所以,则,而,所以;
由,得,由,得,再证明,则,所以,则,由三角形的中位线定理得,于是得到问题的答案.
23.【答案】解: 不是“勾系一元二次方程”,
理由:,
,
,,
,
以、、为三边长的三角形是不是直角三角形,且为斜边的长,
不是“勾系一元二次方程”,
是“勾系一元二次方程”,
理由:,
,
,,
,
以、、为三边长的三角形是直角三角形,且为斜边的长,
是“勾系一元二次方程”,
故答案为:不是,是;
证明:是“勾系一元二次方程“,
、、为同一直角三角形的三边长,且为斜边的长,
,
,
关于的“勾系一元二次方程”必有实数根.
解:是“勾系一元二次方程”的一个根,
,
,
四边形的周长是,
,
,
,
,
,
,
,
,
,
.
面积是.
【解析】【分析】利用“勾系一元二次方程”的定义进行判断即可求解;
由是“勾系一元二次方程“得,因为,所以关于的“勾系一元二次方程”必有实数根;
由是“勾系一元二次方程”的一个根得,整理得,由四边形的周长是,可得,所以,则,则,所以,而,所以,即可求出的值及的值,得到面积.
24.【答案】解:将绕点逆时针旋转得到.
,,,,
四边形是正方形,,
,
故答案为:,;
四边形是正方形,
,,,
,
,
,
又,
,
,
,
,
,
,
故答案为:,;
,,,
,
将绕点逆时针旋转得到.
,,,,
,
,
,
,
又,
,
,
,
,
,
,
的面积,
故答案为:.
【解析】【分析】由旋转的性质可得,,,,可证四边形是正方形,,可求;
由正方形的性质可得,,,可求,可得,由平行线的性质可求,由相似三角形的性质可求出答案;
由勾股定理可求,由旋转的性质可求,,,,通过证明,可求的长,由三角形的面积公式可求解.
25.【答案】解:如图中,连接.
,
,
设,
在中,,
,
解得,
的半径为.
如图中,连接,.
是直径,
,
平分,
,
,
,
,,
,
,,
,
,
.
如图中,连接,.
是的切线,
,
,
,
,
,
,
,
,
,,
,
,
,
,
,
.
【解析】【分析】如图中,连接设,在中,利用勾股定理构建方程即可解决问题.
如图中,连接,证明,推出,解直角三角形求出即可解决问题.
如图中,连接,证明,推出,推出,推出,可得,求出即可解决问题.
第1页,共1页
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1.已知关于的一元二次方程的常数项是,则的值为
( )
A. B. C. 或 D.
2.在中,,,,以为圆心,为半径作,则点与的位置关系是
( )
A. 点在内 B. 点在上 C. 点在外 D. 无法确定
3.下列各组的四条线段,,,是成比例线段的是
( )
A. ,,,
B. ,,,
C. ,,,
D. ,,,
4.以下命题中,两个直角三角形一定相似;两个等边三角形一定相似;两个菱形一定相似;任意两个矩形一定相似;两个正六边形一定相似.其中真命题的个数是
( )
A. 个 B. 个 C. 个 D. 个
5.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点,,都在横线上.若线段,则线段的长是
( )
A. B. C. D.
6.如图,某建筑工程队在工地一边靠墙处,用米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为平方米.为了方便取物,在各个仓库之间留出了米宽的缺口作通道,在平行于墙的一边留下一个米宽的缺口作小门.若设米,则可列方程
( )
A. B.
C. D.
7.如图,的直径与弦的延长线交于点,若,,则等于
( )
A. B. C. D.
8.如图,矩形中,点在边上,,,,点是矩形内一动点,满足,连接绕点逆时针旋转至,连接,则的最小值为
( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
9.在比例尺是的地图上,若某条道路长约为,则它的实际长度约为 .
10.若,则 .
11.鹦鹉螺是一类古老的软体动物.鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例,是自然界最美的鬼斧神工.如图,是的黄金分割点,若线段的长为,则的长为 结果保留根号
12.如图,是的直径,点,在上.若,则 .
13.圆内接四边形中,;则的度数为 .
14.设,是方程的两根,则的值是 .
15.若是一元二次方程的一个解,则的值为 .
16.在中,,,点是的中点,点为上一动点,当 时,与相似.
17.如图,已知,,,,是轴上的点,且,分别过点,,,作轴的垂线交直线于点,,,,连接,,,,,,,依次相交于点,,,,,,,,的面积依次为,,,,则为 .
18.将图中的矩形和正方形纸片沿图中的虚线剪成块,再用这块拼接成如图所示矩形,其中阴影部分为空余部分,若,则的值为 .
三、解答题(本大题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤)
19.本小题分
解方程:
;
.
20.本小题分
在中,请在图中用无刻度的直尺和圆规作图:作直线,使上的各点到、两边的距离相等,设直线与边交于点,在上找一点使不写作法,保留作图痕迹
21.本小题分
某童装专卖店在销售中发现,一款童装每件进价为元,销售价为元时,每天可售出件,为了迎接“双十一”促销活动,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价元,那么平均可多售出件.
在每件盈利不少于元的前提下,要使该童装每天销售获利为元,每件童装应降价多少元?
该童装每天的销售获利能达到元吗?如果能,请写出降价方案;如果不能,请说明理由.
22.本小题分
如图,是的直径,点是劣弧中点,与相交于点连接,,与的延长线相交于点.
求证:是的切线;
求证:;
若,,请直接写出__.
23.本小题分
如图,四边形是证明勾股定理时用到的一个图形,,,是和边长,易知,这时我们把关于的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
判断下列方程是否是“勾系一元二次方程”:
__填“是”或“不是”;
__填“是”或“不是”
求证:关于的“勾系一元二次方程”必有实数根;
若是“勾系一元二次方程”的一个根,且四边形的周长是,求面积.
24.本小题分
综合与实践
动手操作:
如图,在中,,将绕点逆时针旋转得到延长分别交于点,交于点,连接.
思考探究:
__,__;
若,则
__;
__;
开放拓展:
如图,若改变旋转角,已知,,当时,请直接写出的面积为__.
25.本小题分
如图,在平面直角坐标系内,,为轴上两点,以为直径的交轴于,两点,为的中点,弦交轴于点,且点的坐标为,.
求的半径;
动点在的圆周上运动,连接,交于点.
如图,当平分时,求的值;
如图,过点作的切线交轴于点,当点与点,不重合时,是否为定值?若是,请求出其值;若不是,请说明理由.
答案和解析
1.【答案】
【解析】【分析】根据一元二次方程的定义和题意列出满足的条件求解即可.
【解答】解:由题意,
解得:,
故选:.
2.【答案】
【解析】【分析】利用勾股定理求得边的长,然后通过比较与半径的长即可得到结论.
【解答】解:中,,,,
,
,
点在内,
故选:.
3.【答案】
【解析】【分析】根据比例线段的定义,让最小的和最大的相乘,另外两个相乘,看它们的积是否相等,对选项一一分析,即可得出答案.
【解答】解:、,故此选项不符合题意;
、,故此选项不符合题意;
、,故此选项不符合题意;
、,故此选项符合题意,
故选:.
4.【答案】
【解析】【分析】根据相似图形的定义,形状相同的图形是相似图形.具体的说就是对应的角相等,对应边的比相等,对每个命题进行判断.
【解答】解:任意两个直角三角形,不能判断它们的对应角相等,对应边的比相等,所以不一定相似,故原命题为假命题;
任意两个等边三角形,它们的内角相等,对应边的比相等.所以一定相似,故原命题为真命题;
任意两个菱形,只能判断对应边的比相等,不能判断对应的角相等.所以不一定相似,故原命题为假命题;
任意两个矩形,它们的对应角相等,不能判断对应边的比相等.所以不一定相似,故原命题为假命题;
任意两个正六边形,它们的内角相等,对应边的比相等.所以一定相似,故原命题为真命题.
故选:.
5.【答案】
【解析】【分析】过点作平行横线的垂线,交点所在的平行横线于,交点所在的平行横线于,根据平行线分线段成比例定理列出比例式,计算即可.
【解答】详解:过点作平行横线的垂线,交点所在的平行横线于,交点所在的平行横线于,则,
即,
解得:,
.
故选:.
6.【答案】
【解析】【分析】根据铁栅栏的总长及的长,可得出米,根据仓库总面积为平方米,即可列出关于的一元二次方程,解之即可得出结论.
【解答】解:铁栅栏的总长为米,且米,
米,
根据题意得:.
故选:.
7.【答案】
【解析】【分析】利用,得到,则,根据三角形外角性质得,所以,同理得到,然后利用进行计算即可.
【解答】解:连接,如图,
,,
,
,
,
,
而,
,
,
,
.
故选:.
8.【答案】
【解析】【分析】取的中点,再把绕点逆时针旋转至,连接,,,则有,即可求出,然后过点作于点,连接,利用勾股定理可以得到,再根据求出结果.
【解答】解:如图,取的中点,再把绕点逆时针旋转至,连接,,,
,
,
根据旋转可得:,,
,,
,
,
,
,
点在以为圆心,为半径的圆上移动,
过点作于点,连接,
则四边形是矩形,
,,
,
,
,
故选:.
9.【答案】
【解析】【分析】根据比例尺图上距离:实际距离,依题意列比例式直接求解即可.
【解答】解:设它的实际长度约为,则
,
解得,
.
它的实际长度约为.
故答案为:.
10.【答案】
【解析】【分析】利用设法进行计算,即可解答.
【解答】解:设,
,,
,
故答案为:.
11.【答案】
【解析】【分析】根据黄金分割的定义进行计算,即可解答.
【解答】解:是的黄金分割点,,
,
,
故答案为:.
12.【答案】
【解析】【分析】根据圆周角定理得到,,然后利用互余计算出,从而得到的度数.
【解答】解:为的直径,
,
,
,
.
故答案为:.
13.【答案】
【解析】【分析】根据圆内接四边形对角互补求解.
【解答】解:四边形是圆内接四边形,
,
,
.
故答案为:.
14.【答案】
【解析】【分析】根据根与系数的关系,直接代入求解即可得到答案.
【解答】解:,是方程的两根,
,,
,
故答案为:.
15.【答案】
【解析】【分析】把代入方程中得:,从而可得,然后代入式子中进行计算,即可解答.
【解答】解:把代入方程中得:,
,
,
故答案为:.
16.【答案】或
【解析】【分析】根据相似三角形的性质可得比例关系进而得出的值.
【解答】解:和相似时,
或者,
在中,,,点是的中点,
,
,即,
解得,
,即,
解得.
故答案为:或.
17.【答案】
【解析】【分析】根据图象上点的坐标性质得出点、、、、、各点坐标,进而利用相似三角形的判定与性质得出、、、、,进而得出答案.
【解答】解:、、、、、是轴上的点,且,分别过点、、、、、作轴的垂线交直线于点、、、、、,
依题意得:,,,,
,
,
,
与对应高的比为:,
,
边上的高为,
,
同理可得:,,
.
故答案为:.
18.【答案】
【解析】【分析】如图,设,则,,首先证明,利用相似三角形的性质构建关系式,即可解决问题.
【解答】解:如图,设,则,,
,,
,
,
,
,
,
,,
,
,
,
,
整理得,,
,
,
,
.
故答案为:
19.【答案】解:由原方程,得
,
开方,得
,
解得,;
由原方程,得
,
解得,.
【解析】【分析】利用直接开平方法解方程即可;
利用“十字相乘法”对等式的左边进行因式分解,然后解方程.
20.【答案】解:作的平分线,交于点,则直线即为所求作的直;作线段的垂直平分线和以为直径的,与半圆的交点为,连接,与的交点即为点,如图:
【解析】【分析】作的平分线,交于点,则直线即为所求作的直;作线段的垂直平分线和以为直径的,与半圆的交点为,连接,与的交点即为点.
21.【答案】解:设每件童装降价元时,每天可销售件,每件盈利为元,
由题意得:,
整理得:,
解得:,,
当时,每件盈利为:,不合题意,舍去;
当时,每件盈利为:,符合题意;
答:每件童装应降价元;
不能,理由如下:
设童装每天的销售获利为元,
由知,,
当时,的值最大,最大值为,
该童装每天的销售获利不能达到元.
【解析】【分析】设每件童装降价元时,每天可销售件,每件盈利为元,根据总利润每件利润销售数量,列出一元二次方程,解方程并由每件盈利不少于元,即可得出答案;
设童装每天的销售获利为元,根据总利润每件利润销售数量,求最大值即可.
22.【答案】证明:连接交于点,则,
,
,
,
是的直径,
,
是的半径,且,
是的切线.
证明:点是劣弧中点,
,
,
,
,
,
.
解:,,
,
,
,
,,
,
,
,
,
,,
,
故答案为:.
【解析】【分析】连接交于点,由,,得,则,即可证明是的切线;
由点是劣弧中点,根据垂径定理得,则,所以,则,而,所以;
由,得,由,得,再证明,则,所以,则,由三角形的中位线定理得,于是得到问题的答案.
23.【答案】解: 不是“勾系一元二次方程”,
理由:,
,
,,
,
以、、为三边长的三角形是不是直角三角形,且为斜边的长,
不是“勾系一元二次方程”,
是“勾系一元二次方程”,
理由:,
,
,,
,
以、、为三边长的三角形是直角三角形,且为斜边的长,
是“勾系一元二次方程”,
故答案为:不是,是;
证明:是“勾系一元二次方程“,
、、为同一直角三角形的三边长,且为斜边的长,
,
,
关于的“勾系一元二次方程”必有实数根.
解:是“勾系一元二次方程”的一个根,
,
,
四边形的周长是,
,
,
,
,
,
,
,
,
,
.
面积是.
【解析】【分析】利用“勾系一元二次方程”的定义进行判断即可求解;
由是“勾系一元二次方程“得,因为,所以关于的“勾系一元二次方程”必有实数根;
由是“勾系一元二次方程”的一个根得,整理得,由四边形的周长是,可得,所以,则,则,所以,而,所以,即可求出的值及的值,得到面积.
24.【答案】解:将绕点逆时针旋转得到.
,,,,
四边形是正方形,,
,
故答案为:,;
四边形是正方形,
,,,
,
,
,
又,
,
,
,
,
,
,
故答案为:,;
,,,
,
将绕点逆时针旋转得到.
,,,,
,
,
,
,
又,
,
,
,
,
,
,
的面积,
故答案为:.
【解析】【分析】由旋转的性质可得,,,,可证四边形是正方形,,可求;
由正方形的性质可得,,,可求,可得,由平行线的性质可求,由相似三角形的性质可求出答案;
由勾股定理可求,由旋转的性质可求,,,,通过证明,可求的长,由三角形的面积公式可求解.
25.【答案】解:如图中,连接.
,
,
设,
在中,,
,
解得,
的半径为.
如图中,连接,.
是直径,
,
平分,
,
,
,
,,
,
,,
,
,
.
如图中,连接,.
是的切线,
,
,
,
,
,
,
,
,
,,
,
,
,
,
,
.
【解析】【分析】如图中,连接设,在中,利用勾股定理构建方程即可解决问题.
如图中,连接,证明,推出,解直角三角形求出即可解决问题.
如图中,连接,证明,推出,推出,推出,可得,求出即可解决问题.
第1页,共1页
同课章节目录
