2023-2024学年江苏省无锡市新吴区梅里集团校九年级(上)期中数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年江苏省无锡市新吴区梅里集团校九年级(上)期中数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 358.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览



文档简介
2023-2024学年江苏省无锡市新吴区梅里集团校九年级(上)期中数学试卷
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.下列方程是一元二次方程的是
( )
A. B. C. D.
2.已知四边形是圆内接四边形,,则的度数为
( )
A. B. C. D.
3.我市某中学开展“经典诵读”比赛活动,班在此次比赛中的得分分别是:,,,,,,,,这组数据的众数和中位数分别是
( )
A. , B. , C. , D. ,
4.若的内接正边形的边长与的半径相等,则的值为
( )
A. B. C. D.
5.某网络学习平台年的新注册用户数为万,年的新注册用户数为万,设新注册用户数的年平均增长率为,根据题意所列方程正确的是
( )
A. B.
C. D.
6.如图,已知是半圆的直径,,是弧的中点,那么的度数是
( )
A. B. C. D.
7.下列命题中,真命题的个数是
( )
长度相等的弧是等弧
相等的圆心角所对的弦相等
等边三角形的外心与内心重合
任意三点可以确定一个圆
三角形有且只有一个外接圆
A. B. C. D.
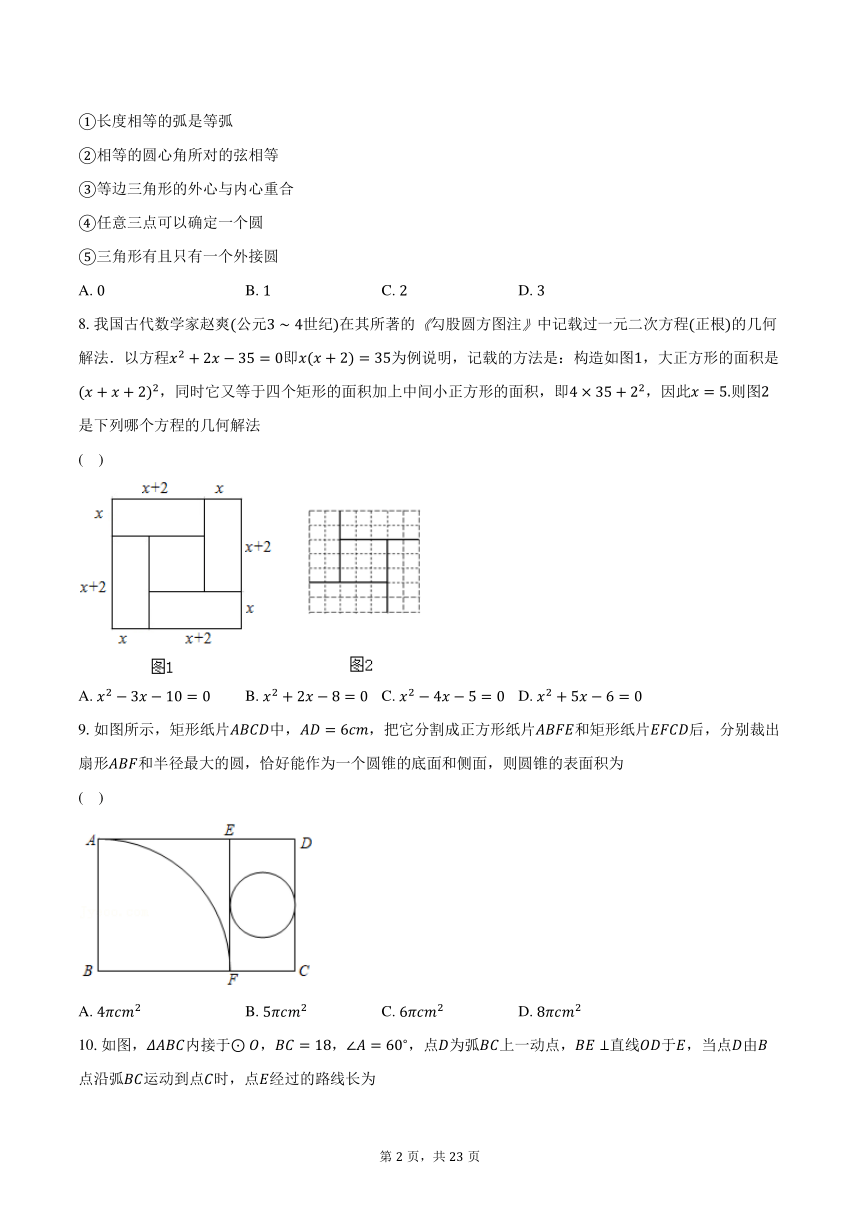
8.我国古代数学家赵爽公元世纪在其所著的勾股圆方图注中记载过一元二次方程正根的几何解法.以方程即为例说明,记载的方法是:构造如图,大正方形的面积是,同时它又等于四个矩形的面积加上中间小正方形的面积,即,因此则图是下列哪个方程的几何解法
( )
A. B. C. D.
9.如图所示,矩形纸片中,,把它分割成正方形纸片和矩形纸片后,分别裁出扇形和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则圆锥的表面积为
( )
A. B. C. D.
10.如图,内接于,,,点为弧上一动点,直线于,当点由点沿弧运动到点时,点经过的路线长为
( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
11.已知关于的方程有两个不相等的实数根,则的取值范围是 .
12.有一枚质地均匀的骰子,骰子各个面上的点数分别为任意抛掷这枚骰子,朝上面的点数大于的概率是 .
13.如图,若圆锥的母线长为,底面半径为,则其侧面展开图的圆心角为 .
14.设,分别是方程的两个实数根,则的值是 .
15.如图,点、、在上,,则的度数是 .
16.某电视台要招聘名记者,某应聘者参加了项素质测试,成绩如下:
测试项目 采访写作 计算机操作 创意设计
测试成绩分
如果将采访写作、计算机操作和创意设计的成绩按计算,则该应聘者的素质测试平均成绩是 分.
17.如图,已知与的斜边交于,两点,、恰好是的三等分点,若的半径等于,则 ,的长为 .
18.如图,在平面直角坐标系中,已知,以点为圆心的圆与轴相切.点、在轴上,且点为上的动点,,则长度的最大值为 .
三、解答题(本大题共10小题,共80分。解答应写出文字说明,证明过程或演算步骤)
19.本小题分
解方程:
;
配方法;
;
.
20.本小题分
已知关于的一元二次方程.
求证:方程总有两个不相等的实数根.
若此方程的一个根是,求出方程的另一个根及的值.
21.本小题分
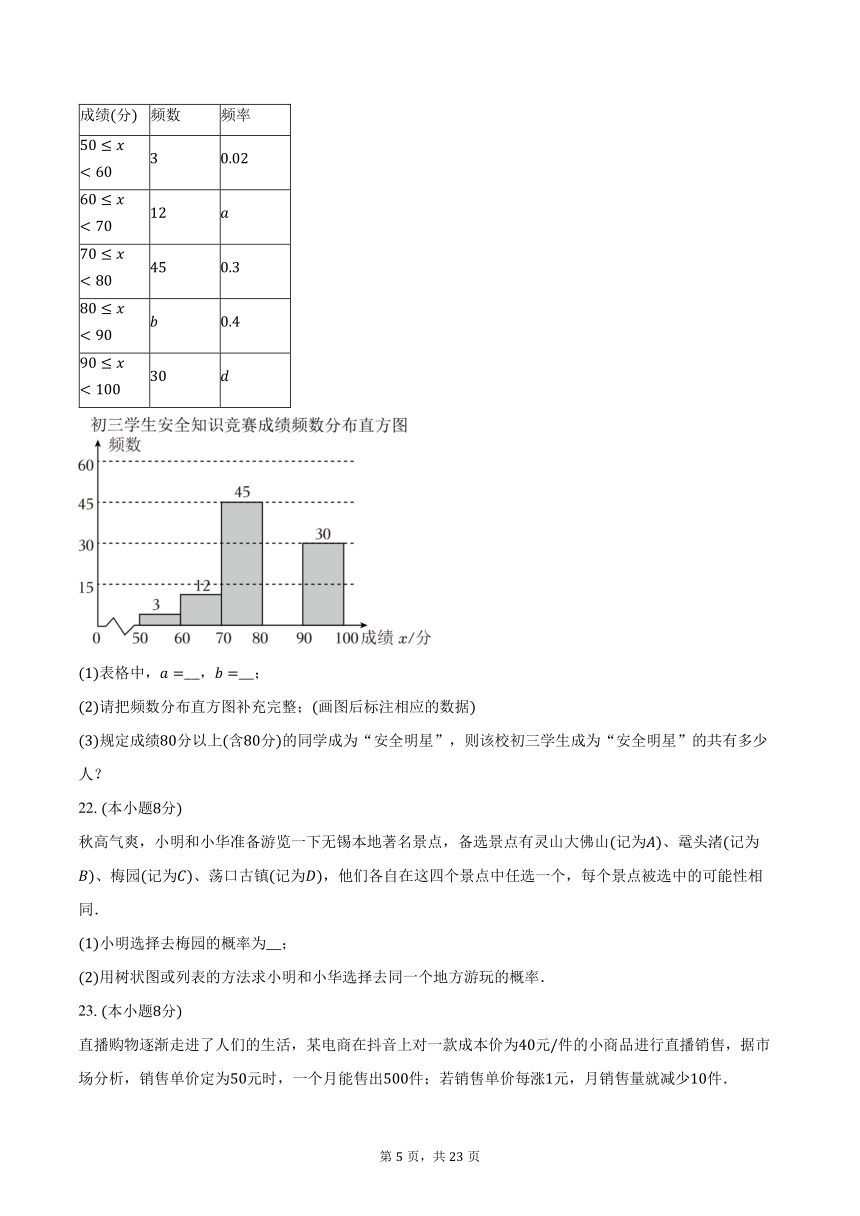
某校为了了解初三学生对安全知识的掌握情况,加强学生的安全防范和自我保护意识,对该校名初三学生开展安全知识竞赛活动.用简单随机抽样的方法,随机抽取若干名学生统计答题成绩,分别制成如下频数分布表和频数分布直方图:
初三学生安全知识竞赛成绩频数分布表
成绩分 频数 频率
表格中,__,__;
请把频数分布直方图补充完整;画图后标注相应的数据
规定成绩分以上含分的同学成为“安全明星”,则该校初三学生成为“安全明星”的共有多少人?
22.本小题分
秋高气爽,小明和小华准备游览一下无锡本地著名景点,备选景点有灵山大佛山记为、鼋头渚记为、梅园记为、荡口古镇记为,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同.
小明选择去梅园的概率为__;
用树状图或列表的方法求小明和小华选择去同一个地方游玩的概率.
23.本小题分
直播购物逐渐走进了人们的生活,某电商在抖音上对一款成本价为元件的小商品进行直播销售,据市场分析,销售单价定为元时,一个月能售出件;若销售单价每涨元,月销售量就减少件.
若实际单价定为元,则一个月的利润为__元;
针对这种小家电的销售情况,该商店要保证每月盈利元,同时又要使顾客得到实惠,那么销售单价应定为多少元?
24.本小题分
如图,已知是锐角三角形.
利用直尺与圆规画出的外接圆保留作图痕迹
利用直尺与圆规画出中经过点的的切线保留作图痕迹
25.本小题分
如图,为的直径,点在上,延长至点,使,延长与的另一个交点为,连接,.
求证:;
若,,求的长.
26.本小题分
如图,四边形内接于,是的直径,过点作,垂足为点,平分.
判断与的位置关系,并说明理由;
若,的半径为,请求出图中阴影部分的面积.
27.本小题分
如果关于的一元二次方程有两个实数根,且其中一个根为另一个根的倍,那么称这样的方程为“倍根方程”例如,一元二次方程的两个根是和,则方程就是“倍根方程”.
若一元二次方程是“倍根方程”,则__;
若是“倍根方程”,求代数式的值;
若关于的一元二次方程是“倍根方程”,求,,之间的关系.
28.本小题分
如图,已知线段,于点,且,是射线上一动点,,分别是,的中点,过点,,的圆与的另一交点点在线段上,与的另一个交点,连接,
当时,求的度数和弧的度数.
求证:.
若,点为射线上的一个动点,
求的值;
在点的运动过程中,取四边形一边的两端点和线段上一点,若以这三点为顶点的三角形是直角三角形,且为锐角顶点,求此时所有满足条件的的值.
答案和解析
1.【答案】
【解析】【分析】根据一元二次方程的定义对各选项进行判断.
【解答】解:.为一元二次方程,所以选项符合题意;
.为二元一次方程,所以选项不符合题意;
.为一元三次方程,所以选项不符合题意;
.为二元二次方程,所以选项不符合题意;
故选:.
2.【答案】
【解析】【分析】根据圆内接四边形的对角互补列式计算即可.
【解答】解:四边形是圆内接四边形,
,
,
.
故选:.
3.【答案】
【解析】【分析】先将题目中的数据按照从小到大排列,即可得到这组数据的众数,然后再计算出中位数即可.
【解答】解:将数据,,,,,,,按照从小到大排列是:,,,,,,,,
则这组数据的众数是,中位数是,
故选:.
4.【答案】
【解析】【分析】因为的半径与这个正边形的边长相等,推出这个多边形的中心角,构建方程即可解决问题.
【解答】解:的半径与这个正边形的边长相等,
这个多边形的中心角,
,
,
故选:.
5.【答案】
【解析】【分析】利用该网络学习平台年的新注册用户数该网络学习平台年的新注册用户数新注册用户数的年平均增长率,即可列出关于的一元二次方程,此题得解.
【解答】解:根据题意得:.
故选:.
6.【答案】
【解析】【分析】连接、,如图,先根据圆周角定理得到,再利用得到,接着利用平角的定义计算出,然后根据圆周角定理得到的度数.
【解答】解:连接、,如图,
,
,
是弧的中点,
,
,
,
.
故选:.
7.【答案】
【解析】【分析】根据等弧的概念,圆的相关性质,确定圆的条件逐项判断即可.
【解答】解:能够重合的弧是等弧,故是假命题;
在同圆或等圆中,相等的圆心角所对的弦相等,故是假命题;
等边三角形的外心与内心重合,故是真命题;
不在同一直线上的任意三点可以确定一个圆,故是假命题;
三角形有且只有一个外接圆,故是真命题;
真命题有个;
故选:.
8.【答案】
【解析】【分析】根据题意,观察图,由面积之间的关系可得出答案.
【解答】解:中间小正方形边长为,其面积为,
大正方形面积为,边长为,
图是,即的几何解法,
故选:.
9.【答案】
【解析】【分析】设,则,根据扇形的弧长等于圆锥底面圆的周长列出方程,求解即可.
【解答】解:设,则,
根据题意,得,
解得,
所以圆锥的表面积.
故选:.
10.【答案】
【解析】【分析】当点在以为直径的圆上当点在点时,此时和重合;当沿运动到点和点重合时,连接,则点经过的路径是以为直径的圆上弦所对的优弧的长,进而求解.
【解答】解:作圆的直径,连接,取的中点,连接,如图所示:
为的直径,
,
,
,
,
,
,为的中点.
,
故当点在以为直径的圆上当点在点时,此时和重合;
当沿运动到点和点重合时,连接,
由圆周角定理得:,,,
故点经过的路径是以为直径的圆上弦所对的优弧的长,
由弧长公式得:,
故选:.
11.【答案】
【解析】【分析】关于的方程有两个不相等的实数根,即判别式即可得到关于的不等式,从而求得的范围
【解答】解:,,,
,
解得:.
故答案为:.
12.【答案】
【解析】【分析】由朝上的面的点数有种等可能结果,其中朝上面的点数大于的有,,,共种结果,根据概率公式计算可得.
【解答】解:任意抛掷这枚骰子,朝上的面的点数有种等可能结果,其中朝上面的点数大于的有,,,共种结果,
朝上面的点数大于的概率是.
故答案为:.
13.【答案】
【解析】【分析】设圆锥的侧面展开图的圆心角为,由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,则根据弧长公式得到,然后解方程即可.
【解答】解:设圆锥的侧面展开图的圆心角为,
根据题意得,
解得,
所以侧面展开图的圆心角为.
故答案为:.
14.【答案】
【解析】【分析】根据题意得,即,利用根与系数的关系得到,代入整理后的代数式求值.
【解答】解:,分别是方程的两个实数根,
,,
,
故.
故答案为:.
15.【答案】
【解析】【分析】根据,可以得到的度数,再根据,三角形内角和是,即可得到的度数.
【解答】解:,
,
,
,
,
,
故答案为:.
16.【答案】
【解析】【分析】根据加权平均数的定义计算可得.
【解答】解:该应聘者的素质测试平均成绩是分,
故答案为:.
17.【答案】
【解析】【分析】过作于点,由垂径定理得到,推出是等腰直角三角形,得到,设,根据勾股定理即可得到结论.
【解答】解:过作于点,
,
,
,
是等腰直角三角形,
,,
设,
,
,
,
,
,
故答案为:,.
18.【答案】
【解析】【分析】连接并延长,交上一点,以为圆心,以为半径作,交轴于、,此时的长度最大,根据勾股定理和题意求得,则的最大长度为.
【解答】解:连接并延长,交上一点,以为圆心,以为半径作,交轴于、,此时的长度最大,
,
,
以点为圆心的圆与轴相切.
的半径为,
,
,
长度的最大值为,
故答案为.
19.【答案】解:,
,
,
,;
,
,
,
,
,
,;
,
,
或,
,;
,
,
,
或,
,.
【解析】【分析】利用解一元二次方程直接开平方法进行计算,即可解答;
利用解一元二次方程配方法进行计算,即可解答;
利用解一元二次方程因式分解法进行计算,即可解答;
利用解一元二次方程因式分解法进行计算,即可解答
20.【答案】证明:,
而,
.
方程总有两个不相等的实数根;
解:方程的一个根是,
,
解得:,
原方程为:,
解得:,.
即的值为,方程的另一个根是.
【解析】【分析】要证明方程有两个不相等的实数根,即证明即可.,因为,可以得到;
将代入方程,求出的值,进而得出方程的解.
21.【答案】解:样本容量为,
,,
则.
故答案为:、;
频数分布图如图所示:
该校初三学生成为“安全明星”的共有人.
答:该校初三学生成为“安全明星”的估计有人.
【解析】【分析】先根据的频数及频率求出样本容量,可得结论;
根据中结论,画出图形即可.
用总人数乘以成绩分以上含分的人数所占比例即可.
22.【答案】解:由题意得,小明选择去梅园的概率为.
故答案为:.
画树状图如下:
共有种等可能的结果,其中小明和小华选择去同一个地方游玩的结果有种,
小明和小华选择去同一个地方游玩的概率为.
【解析】【分析】直接利用概率公式可得答案.
画树状图得出所有等可能的结果数以及小明和小华选择去同一个地方游玩的结果数,再利用概率公式可得出答案.
23.【答案】解:根据题意可知,元;
故答案为:;
设销售单价应定为元,根据题意得
整理得,
解得,,要使顾客得到实惠,
答:销售单价应定为元.
【解析】【分析】利用原来的销售量减去减少的销售量得到每月销售量,再乘每个家电的利润即可得出结论;
设销售单价定为元,根据题意可列出方程,解之即可.
24.【答案】解:如图即为所求.
如图直线,即为的切线.
【解析】【分析】任意两边的垂直平分的交点,即为外接圆的圆心.
过点作垂直于的直线,即为的切线.
25.【答案】证明:为的直径,
,即,
,
,
,
,
;
解:在中,,,由勾股定理得:,
解得:负根已经舍去,,
,
即,
由圆周角定理得:,
又,
,
,
,
.
【解析】【分析】根据圆周角定理求出,根据线段垂直平分线的性质得出,根据等腰三角形的性质得出即可;
根据勾股定理求出和,求出,求出,根据等腰三角形的判定得出,即可求出答案.
26.【答案】解:与相切,
理由:连接,
,
,
平分,
,
,
,
,
,
,即,
,
与相切;
,
,
,
是等边三角形,
,,
,
,,
.
【解析】【分析】连接,根据等腰三角形的性质、角平分线的定义得到,证明,根据切线的判定定理证明即可;
证明是等边三角形,得到,根据勾股定理求出、,根据梯形的面积公式、扇形的面积公式计算即可.
27.【答案】解:一元二次方程是“倍根方程”,
,,即,,
,
故答案为:;
解方程得,,.
方程两根是倍关系,
或,
当时,,即,
代入代数式,
当时,,即,
代入代数式.
综上所述,;
根据“倍根方程”的概念设一元二次方程的两个根为和.
原方程可以改写为,
,
.
解得.
,,之间的关系是.
【解析】【分析】由一元二次方程是“倍根方程”,得到,,即可得到结论;
解方程得,,由方程两根是倍关系,得到或,代入解方程即可得到结论;
根据“倍根方程”的概念得到原方程可以改写为,解方程即可得到结论.
28.【答案】解:,,
,
,
,
,
如图,连接,
为的中位线,
,
,
;
,
又,,
,
,
,
;
如图,记与圆的另一个交点为,
是的中线,
,
,
,
,
,
,
,
,
,
Ⅰ当时,为圆的直径,
与重合,
;
Ⅱ如图,当时,
在中,,
;
Ⅲ如图,当时,
,,
,
,
,
,
,
Ⅳ如图,当时,
由对称性可得,
;
综上所述,的值为或或.
【解析】【分析】连接,结合垂直平分线的性质与等腰三角形性质结合三角形内角和定理,中位线定理求解即可;
求证即可;
连接,,结合勾股定理求解即可;分为当时;当时;当时;当时,分类讨论即可.
第1页,共1页
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.下列方程是一元二次方程的是
( )
A. B. C. D.
2.已知四边形是圆内接四边形,,则的度数为
( )
A. B. C. D.
3.我市某中学开展“经典诵读”比赛活动,班在此次比赛中的得分分别是:,,,,,,,,这组数据的众数和中位数分别是
( )
A. , B. , C. , D. ,
4.若的内接正边形的边长与的半径相等,则的值为
( )
A. B. C. D.
5.某网络学习平台年的新注册用户数为万,年的新注册用户数为万,设新注册用户数的年平均增长率为,根据题意所列方程正确的是
( )
A. B.
C. D.
6.如图,已知是半圆的直径,,是弧的中点,那么的度数是
( )
A. B. C. D.
7.下列命题中,真命题的个数是
( )
长度相等的弧是等弧
相等的圆心角所对的弦相等
等边三角形的外心与内心重合
任意三点可以确定一个圆
三角形有且只有一个外接圆
A. B. C. D.
8.我国古代数学家赵爽公元世纪在其所著的勾股圆方图注中记载过一元二次方程正根的几何解法.以方程即为例说明,记载的方法是:构造如图,大正方形的面积是,同时它又等于四个矩形的面积加上中间小正方形的面积,即,因此则图是下列哪个方程的几何解法
( )
A. B. C. D.
9.如图所示,矩形纸片中,,把它分割成正方形纸片和矩形纸片后,分别裁出扇形和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则圆锥的表面积为
( )
A. B. C. D.
10.如图,内接于,,,点为弧上一动点,直线于,当点由点沿弧运动到点时,点经过的路线长为
( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
11.已知关于的方程有两个不相等的实数根,则的取值范围是 .
12.有一枚质地均匀的骰子,骰子各个面上的点数分别为任意抛掷这枚骰子,朝上面的点数大于的概率是 .
13.如图,若圆锥的母线长为,底面半径为,则其侧面展开图的圆心角为 .
14.设,分别是方程的两个实数根,则的值是 .
15.如图,点、、在上,,则的度数是 .
16.某电视台要招聘名记者,某应聘者参加了项素质测试,成绩如下:
测试项目 采访写作 计算机操作 创意设计
测试成绩分
如果将采访写作、计算机操作和创意设计的成绩按计算,则该应聘者的素质测试平均成绩是 分.
17.如图,已知与的斜边交于,两点,、恰好是的三等分点,若的半径等于,则 ,的长为 .
18.如图,在平面直角坐标系中,已知,以点为圆心的圆与轴相切.点、在轴上,且点为上的动点,,则长度的最大值为 .
三、解答题(本大题共10小题,共80分。解答应写出文字说明,证明过程或演算步骤)
19.本小题分
解方程:
;
配方法;
;
.
20.本小题分
已知关于的一元二次方程.
求证:方程总有两个不相等的实数根.
若此方程的一个根是,求出方程的另一个根及的值.
21.本小题分
某校为了了解初三学生对安全知识的掌握情况,加强学生的安全防范和自我保护意识,对该校名初三学生开展安全知识竞赛活动.用简单随机抽样的方法,随机抽取若干名学生统计答题成绩,分别制成如下频数分布表和频数分布直方图:
初三学生安全知识竞赛成绩频数分布表
成绩分 频数 频率
表格中,__,__;
请把频数分布直方图补充完整;画图后标注相应的数据
规定成绩分以上含分的同学成为“安全明星”,则该校初三学生成为“安全明星”的共有多少人?
22.本小题分
秋高气爽,小明和小华准备游览一下无锡本地著名景点,备选景点有灵山大佛山记为、鼋头渚记为、梅园记为、荡口古镇记为,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同.
小明选择去梅园的概率为__;
用树状图或列表的方法求小明和小华选择去同一个地方游玩的概率.
23.本小题分
直播购物逐渐走进了人们的生活,某电商在抖音上对一款成本价为元件的小商品进行直播销售,据市场分析,销售单价定为元时,一个月能售出件;若销售单价每涨元,月销售量就减少件.
若实际单价定为元,则一个月的利润为__元;
针对这种小家电的销售情况,该商店要保证每月盈利元,同时又要使顾客得到实惠,那么销售单价应定为多少元?
24.本小题分
如图,已知是锐角三角形.
利用直尺与圆规画出的外接圆保留作图痕迹
利用直尺与圆规画出中经过点的的切线保留作图痕迹
25.本小题分
如图,为的直径,点在上,延长至点,使,延长与的另一个交点为,连接,.
求证:;
若,,求的长.
26.本小题分
如图,四边形内接于,是的直径,过点作,垂足为点,平分.
判断与的位置关系,并说明理由;
若,的半径为,请求出图中阴影部分的面积.
27.本小题分
如果关于的一元二次方程有两个实数根,且其中一个根为另一个根的倍,那么称这样的方程为“倍根方程”例如,一元二次方程的两个根是和,则方程就是“倍根方程”.
若一元二次方程是“倍根方程”,则__;
若是“倍根方程”,求代数式的值;
若关于的一元二次方程是“倍根方程”,求,,之间的关系.
28.本小题分
如图,已知线段,于点,且,是射线上一动点,,分别是,的中点,过点,,的圆与的另一交点点在线段上,与的另一个交点,连接,
当时,求的度数和弧的度数.
求证:.
若,点为射线上的一个动点,
求的值;
在点的运动过程中,取四边形一边的两端点和线段上一点,若以这三点为顶点的三角形是直角三角形,且为锐角顶点,求此时所有满足条件的的值.
答案和解析
1.【答案】
【解析】【分析】根据一元二次方程的定义对各选项进行判断.
【解答】解:.为一元二次方程,所以选项符合题意;
.为二元一次方程,所以选项不符合题意;
.为一元三次方程,所以选项不符合题意;
.为二元二次方程,所以选项不符合题意;
故选:.
2.【答案】
【解析】【分析】根据圆内接四边形的对角互补列式计算即可.
【解答】解:四边形是圆内接四边形,
,
,
.
故选:.
3.【答案】
【解析】【分析】先将题目中的数据按照从小到大排列,即可得到这组数据的众数,然后再计算出中位数即可.
【解答】解:将数据,,,,,,,按照从小到大排列是:,,,,,,,,
则这组数据的众数是,中位数是,
故选:.
4.【答案】
【解析】【分析】因为的半径与这个正边形的边长相等,推出这个多边形的中心角,构建方程即可解决问题.
【解答】解:的半径与这个正边形的边长相等,
这个多边形的中心角,
,
,
故选:.
5.【答案】
【解析】【分析】利用该网络学习平台年的新注册用户数该网络学习平台年的新注册用户数新注册用户数的年平均增长率,即可列出关于的一元二次方程,此题得解.
【解答】解:根据题意得:.
故选:.
6.【答案】
【解析】【分析】连接、,如图,先根据圆周角定理得到,再利用得到,接着利用平角的定义计算出,然后根据圆周角定理得到的度数.
【解答】解:连接、,如图,
,
,
是弧的中点,
,
,
,
.
故选:.
7.【答案】
【解析】【分析】根据等弧的概念,圆的相关性质,确定圆的条件逐项判断即可.
【解答】解:能够重合的弧是等弧,故是假命题;
在同圆或等圆中,相等的圆心角所对的弦相等,故是假命题;
等边三角形的外心与内心重合,故是真命题;
不在同一直线上的任意三点可以确定一个圆,故是假命题;
三角形有且只有一个外接圆,故是真命题;
真命题有个;
故选:.
8.【答案】
【解析】【分析】根据题意,观察图,由面积之间的关系可得出答案.
【解答】解:中间小正方形边长为,其面积为,
大正方形面积为,边长为,
图是,即的几何解法,
故选:.
9.【答案】
【解析】【分析】设,则,根据扇形的弧长等于圆锥底面圆的周长列出方程,求解即可.
【解答】解:设,则,
根据题意,得,
解得,
所以圆锥的表面积.
故选:.
10.【答案】
【解析】【分析】当点在以为直径的圆上当点在点时,此时和重合;当沿运动到点和点重合时,连接,则点经过的路径是以为直径的圆上弦所对的优弧的长,进而求解.
【解答】解:作圆的直径,连接,取的中点,连接,如图所示:
为的直径,
,
,
,
,
,
,为的中点.
,
故当点在以为直径的圆上当点在点时,此时和重合;
当沿运动到点和点重合时,连接,
由圆周角定理得:,,,
故点经过的路径是以为直径的圆上弦所对的优弧的长,
由弧长公式得:,
故选:.
11.【答案】
【解析】【分析】关于的方程有两个不相等的实数根,即判别式即可得到关于的不等式,从而求得的范围
【解答】解:,,,
,
解得:.
故答案为:.
12.【答案】
【解析】【分析】由朝上的面的点数有种等可能结果,其中朝上面的点数大于的有,,,共种结果,根据概率公式计算可得.
【解答】解:任意抛掷这枚骰子,朝上的面的点数有种等可能结果,其中朝上面的点数大于的有,,,共种结果,
朝上面的点数大于的概率是.
故答案为:.
13.【答案】
【解析】【分析】设圆锥的侧面展开图的圆心角为,由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,则根据弧长公式得到,然后解方程即可.
【解答】解:设圆锥的侧面展开图的圆心角为,
根据题意得,
解得,
所以侧面展开图的圆心角为.
故答案为:.
14.【答案】
【解析】【分析】根据题意得,即,利用根与系数的关系得到,代入整理后的代数式求值.
【解答】解:,分别是方程的两个实数根,
,,
,
故.
故答案为:.
15.【答案】
【解析】【分析】根据,可以得到的度数,再根据,三角形内角和是,即可得到的度数.
【解答】解:,
,
,
,
,
,
故答案为:.
16.【答案】
【解析】【分析】根据加权平均数的定义计算可得.
【解答】解:该应聘者的素质测试平均成绩是分,
故答案为:.
17.【答案】
【解析】【分析】过作于点,由垂径定理得到,推出是等腰直角三角形,得到,设,根据勾股定理即可得到结论.
【解答】解:过作于点,
,
,
,
是等腰直角三角形,
,,
设,
,
,
,
,
,
故答案为:,.
18.【答案】
【解析】【分析】连接并延长,交上一点,以为圆心,以为半径作,交轴于、,此时的长度最大,根据勾股定理和题意求得,则的最大长度为.
【解答】解:连接并延长,交上一点,以为圆心,以为半径作,交轴于、,此时的长度最大,
,
,
以点为圆心的圆与轴相切.
的半径为,
,
,
长度的最大值为,
故答案为.
19.【答案】解:,
,
,
,;
,
,
,
,
,
,;
,
,
或,
,;
,
,
,
或,
,.
【解析】【分析】利用解一元二次方程直接开平方法进行计算,即可解答;
利用解一元二次方程配方法进行计算,即可解答;
利用解一元二次方程因式分解法进行计算,即可解答;
利用解一元二次方程因式分解法进行计算,即可解答
20.【答案】证明:,
而,
.
方程总有两个不相等的实数根;
解:方程的一个根是,
,
解得:,
原方程为:,
解得:,.
即的值为,方程的另一个根是.
【解析】【分析】要证明方程有两个不相等的实数根,即证明即可.,因为,可以得到;
将代入方程,求出的值,进而得出方程的解.
21.【答案】解:样本容量为,
,,
则.
故答案为:、;
频数分布图如图所示:
该校初三学生成为“安全明星”的共有人.
答:该校初三学生成为“安全明星”的估计有人.
【解析】【分析】先根据的频数及频率求出样本容量,可得结论;
根据中结论,画出图形即可.
用总人数乘以成绩分以上含分的人数所占比例即可.
22.【答案】解:由题意得,小明选择去梅园的概率为.
故答案为:.
画树状图如下:
共有种等可能的结果,其中小明和小华选择去同一个地方游玩的结果有种,
小明和小华选择去同一个地方游玩的概率为.
【解析】【分析】直接利用概率公式可得答案.
画树状图得出所有等可能的结果数以及小明和小华选择去同一个地方游玩的结果数,再利用概率公式可得出答案.
23.【答案】解:根据题意可知,元;
故答案为:;
设销售单价应定为元,根据题意得
整理得,
解得,,要使顾客得到实惠,
答:销售单价应定为元.
【解析】【分析】利用原来的销售量减去减少的销售量得到每月销售量,再乘每个家电的利润即可得出结论;
设销售单价定为元,根据题意可列出方程,解之即可.
24.【答案】解:如图即为所求.
如图直线,即为的切线.
【解析】【分析】任意两边的垂直平分的交点,即为外接圆的圆心.
过点作垂直于的直线,即为的切线.
25.【答案】证明:为的直径,
,即,
,
,
,
,
;
解:在中,,,由勾股定理得:,
解得:负根已经舍去,,
,
即,
由圆周角定理得:,
又,
,
,
,
.
【解析】【分析】根据圆周角定理求出,根据线段垂直平分线的性质得出,根据等腰三角形的性质得出即可;
根据勾股定理求出和,求出,求出,根据等腰三角形的判定得出,即可求出答案.
26.【答案】解:与相切,
理由:连接,
,
,
平分,
,
,
,
,
,
,即,
,
与相切;
,
,
,
是等边三角形,
,,
,
,,
.
【解析】【分析】连接,根据等腰三角形的性质、角平分线的定义得到,证明,根据切线的判定定理证明即可;
证明是等边三角形,得到,根据勾股定理求出、,根据梯形的面积公式、扇形的面积公式计算即可.
27.【答案】解:一元二次方程是“倍根方程”,
,,即,,
,
故答案为:;
解方程得,,.
方程两根是倍关系,
或,
当时,,即,
代入代数式,
当时,,即,
代入代数式.
综上所述,;
根据“倍根方程”的概念设一元二次方程的两个根为和.
原方程可以改写为,
,
.
解得.
,,之间的关系是.
【解析】【分析】由一元二次方程是“倍根方程”,得到,,即可得到结论;
解方程得,,由方程两根是倍关系,得到或,代入解方程即可得到结论;
根据“倍根方程”的概念得到原方程可以改写为,解方程即可得到结论.
28.【答案】解:,,
,
,
,
,
如图,连接,
为的中位线,
,
,
;
,
又,,
,
,
,
;
如图,记与圆的另一个交点为,
是的中线,
,
,
,
,
,
,
,
,
,
Ⅰ当时,为圆的直径,
与重合,
;
Ⅱ如图,当时,
在中,,
;
Ⅲ如图,当时,
,,
,
,
,
,
,
Ⅳ如图,当时,
由对称性可得,
;
综上所述,的值为或或.
【解析】【分析】连接,结合垂直平分线的性质与等腰三角形性质结合三角形内角和定理,中位线定理求解即可;
求证即可;
连接,,结合勾股定理求解即可;分为当时;当时;当时;当时,分类讨论即可.
第1页,共1页
同课章节目录
