第六单元 百分数复习课件2(共32张PPT)023-2024学年六年级数学上册期末核心考点集训(苏教版)
文档属性
| 名称 | 第六单元 百分数复习课件2(共32张PPT)023-2024学年六年级数学上册期末核心考点集训(苏教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 08:46:07 | ||
图片预览









文档简介
(共32张PPT)
第六单元 百分数
期末考点集训
2023-2024学年苏教版数学六年级上册
知识点01:百分数的意义和读写
1.百分数的意义:表示一个数是另一个数的百分之几的数,百分数又叫作百分比或百分率。
2.百分数的读法:先读百分号(分母),读成“百分之”,再读百分号前面的数(分子)。
3.百分数的写法:百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示。
知识点02:百分数、小数和分数的互化
1. 百分数与小数的互化
(1)小数化成百分数,将它的小数点向右移动两位,同时在末尾添上百分号。
(2)百分数化成小数,小数点向左移动两位,同时去掉百分号。在移动小数点的过程中,如果位数不够,添0补足。
2. 百分数与分数的互化
(1)把分数化成百分数,先把分数化成小数,再把小数化成百分数。
(2)百分数化成分数,先把百分数改写成分母是100的分数,再化成最简分数。
知识解读
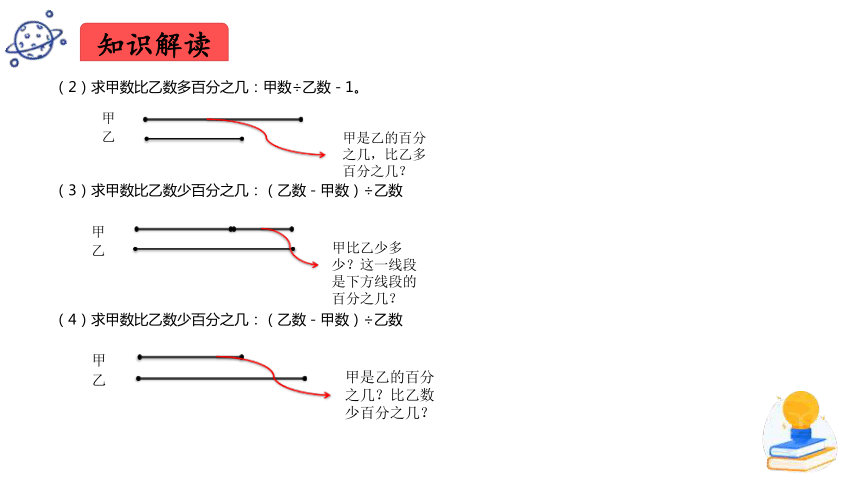
知识点03:求百分率的实际问题
1.求一个数是另一个数的百分之几的实际问题
求一个数是另一个数的百分之几的解题方法与求一个数是另一个数的几分之几的解题方法相同,都用除法计算。
2. 求百分率
求百分率就是求一个数是另一个数的百分之几,用除法计算。
3. 求一个数比另一个数多(少)百分之几
(1)求甲数比乙数多百分之几:(甲数-乙数)÷乙数
知识解读
(2)求甲数比乙数多百分之几:甲数÷乙数-1。
(3)求甲数比乙数少百分之几:(乙数-甲数)÷乙数
(4)求甲数比乙数少百分之几:(乙数-甲数)÷乙数
知识解读
知识点04:百分数的实际应用
1.应纳税额的计算方法:求应纳税额就是求一个数的百分之几是多少,用乘法计算:应纳税额=营业额×税率
2.利息的计算方法:求应纳税额就是求一个数的百分之几是多少,用乘法计算:应纳税额=营业额×税率
3. 折扣问题的解法:解决折扣问题,首先看是打几折,打几折就是按原价的百分之几十出售。现价=原价×折扣
知识点05:列方程解应用题
1. 已知部分数占总数的百分之几和另一部分数,求总数
在实际问题中,要找准把哪个数量看做单位“1”,单位“1”未知时,通常设单位“1”为x,先找出题目中的数量关系,再列方程解决问题。
2. 已知一个数比另一个数多百分之几,求另一个数
在列方程解决倍、差问题时,要注意先找准单位“1”的量,通常情况下设单位“1”的量为x,再根据另一个量与单位“1”的量之间的关系,用含有x的式子表示出另一个量,最后根据它们的和或差列出方程求解。
知识解读
易错点01:百分数的认识、互化、合格率
1.写百分数时,要将分母写成百分号“% ”,分子写在百分号前面。
2.百分数表示的是两个数量之间的倍比关系,只表示两个数量之间的关系,既不能表示具体的数量,也不能带单位名称。
3.将整数改写成百分数时,因为添上百分号后,得到的数就缩小到原来的百分之一,所以要先把原数扩大到原来的100倍,才能保证原数的大小不变。
4.将百分数化成小数,去掉百分号后,一定要将小数点向左移动两位,位数不够时,用“0”补足。
5.将分数化成百分数,用分子除以分母,在除不尽保留近似值时应该用“≈”连接,在将近似值化成百分数应该用“=”连接。
易错点02:百分率及其应用
1.求百分率实质上是求一个数是另一个数的百分之几,只是在计算时要乘100%,把结果化成百分数。
2.及格率、合格率、命中率、出勤率、成活率、出粉率都不能大于100%。
3.“降低了”是指原有数量中减少的部分;“降低到”是指从原有数量中减去一部分后得到的数量。
易错点03:税率利率折扣问题
1.任何一种存款,在计算利息时,都要乘存入时间。
2.商品打折后,比原价降低的金额=原价-现价。
3.解决有关百分数的实际问题,在找准单位“1”的同时,还要看清所要求的问题与单位“1”的关系。
易错点拨
【考点01】百分数的意义、读写及应用
【考点02】小数、分数和百分数之间的关系及其转化
【考点03】增长率变化率问题
【考点04】折扣问题
【考点05】成数问题
【考点06】利率问题
【考点07】税率问题
【考点08】利润率问题
考点目录
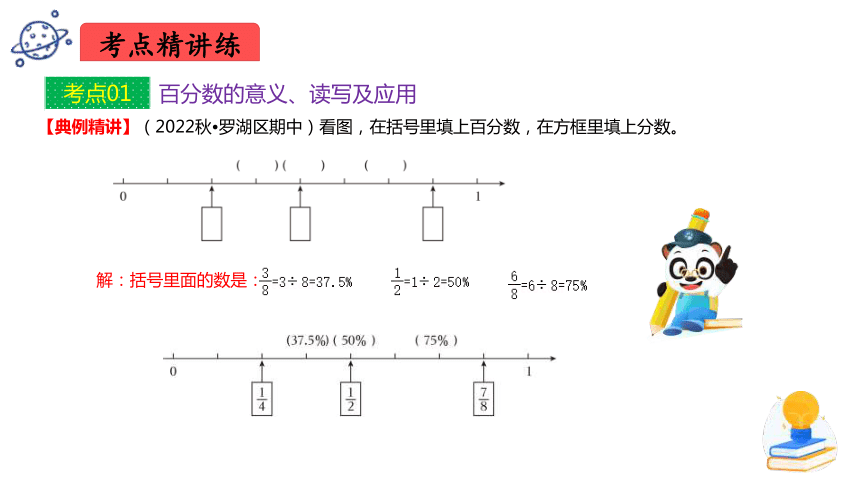
【典例精讲】(2022秋 罗湖区期中)看图,在括号里填上百分数,在方框里填上分数。
考点精讲练
考点01 百分数的意义、读写及应用
解:括号里面的数是:
【真题强化1-1】(2023 洛龙区)下列事件中的百分率可能大于100%的是( )
A.栽种120棵树的成活率
B.六一班学生参加书法比赛的获奖率
C.小麦的出粉率
D.2023年某超市营业额的增长率
考点精讲练
考点01 百分数的意义、读写及应用
解:因为超市营业额可能超过去年的,因此某超市今年的销售额是去年的百分之几可能大于100%。成活率和获奖率最高是100%,出粉率不能达到100%。
故选:D。
【真题强化1-2】(2022秋 三河市期末)我们可以用很多方式描述两个数之间的关系,除了用大于、小于、等于、多和少之外,还可以用倍、分数、比和百分数描述数之间的关系。如果将2、3、5、6、8分别和4进行比较,我们可以说2是4的 %,3是4的,5比4多 ,6和4的比为( : ),
8是4的 倍。
考点精讲练
考点01 百分数的意义、读写及应用
解:2÷4 3÷4= (5﹣1)÷4
=0.5 6:4=3:2
=50% 8÷4=2
=1÷4
=
答:2是4的50%,3是4的 ,5比4多 ,6和4的比为3:2,8是4的2倍。
故答案为:50; ; ;3,2;2。
【典例精讲】(2023 都江堰市)0.75里面有 个0.01
2:5= = %= (填小数)
考点精讲练
考点02 小数、分数和百分数之间的关系及其转化
解:0.75里面有75个0.01
2:5= =40%=0.4
故答案为:75,40,0.4。
【真题强化2-1】(2023 都江堰市)0.75里面有 个0.01
2:5= = %= (填小数)
考点精讲练
考点02 小数、分数和百分数之间的关系及其转化
解:0.75里面有75个0.01
2:5= =40%=0.4
故答案为:75,40,0.4。
【真题强化2-2】(2023 陆丰市)一个数由5个十分之一和3个百分之一组成,这个数写成小数是 ,写成分数是 ,写成百分数是 。
考点精讲练
考点02 小数、分数和百分数之间的关系及其转化
解:一个数由5个十分之一和3个百分之一组成,这个数写成小数是0.53,写成分数是 ,写成百分数是53%。
故答案为:0.53; ;53%。
【典例精讲】(2023春 义乌市期末)五一期间,商场促销,所有商品一律九折出售。九折是指 是
的 ;某商品原价是320元,打折后卖是 元。
考点精讲练
考点03 增长率变化率问题
解:九折是指售价(或现价)是原价的 ;
320× =288(元)。
故答案为:售价(或现价),原价,288。
【真题强化3-1】(2023 通河县)“低碳生活,绿色出行”,广州2010年亚运会后,许多地方增设路边绿化带,自行车道也有增加,不少市民喜欢骑单车出行,享受绿色环保的出行方式。自行车正逐渐成为人们喜爱的交通工具。某商城的自行车销售量自2016年起逐月增加。据统计,该商城1月份销售自行车75辆,2月份销售自行车90辆。若该商城前4个月自行车销量的月平均增长率相同,则该商城3月份销售多少辆自行车?
考点精讲练
考点03 增长率变化率问题
解:设该商城前4个月自行车销量的月平均增长率位为x,根据题意可得:
75×(1+x)=90
75×(1+x)÷75=90÷75
1+x=1.2
1+x﹣1=1.2﹣1
x=0.2
90×(1+0.2)
=90×1.2
=108(辆) 答:该商城3月份销售108辆自行车。
【真题强化3-2】(2023 安宁区)张村有一块试验田种水稻,今年换种新品种后,产量是2600千克,今年产量比去年增产三成,去年的产量是多少千克?
考点精讲练
考点03 增长率变化率问题
解:2600÷(1+30%)
=2600÷1.3
=2000(千克)
答:去年的产量是2000千克。
【典例精讲】(2020 魏县)某商场五一期间举行优惠销售活动,采取“满一百元送二十元,并且连环赠送”的酬宾方式,即顾客每消费满100元(100元可以是现金,也可以是购物券,或二者合计)就送20元购物券,满200元就送40元购物券,依此类推,现有一位顾客第一次就用了16000元购物,并用所得购物券继续购物,那么他购回的商品大约相当于它们原价的( )
A.75% B.80% C.85% D.90%
考点精讲练
考点04 折扣问题
解:根据题意:这位顾客付的钱数是16 000元;
这位顾客所购买的商品的价值是16000元,赠送的购物券的金额是16000× =3200元,3200元赠送的购物券是:3200×20%=640元,640元赠送的购物券是600× =120元,再送购物券20元,
因而用16000元购买的商品的价值是16000+3200+640+120+20=19980元.因而可以设他购回的商品大约相当于它们原价的百分比是x.
则得方程:19980x=16000,
解得:x≈0.8=80%.
故选:B。
【真题强化4-1】(2022秋 泗洪县期末)妈妈买一条裙子,商场促销打六折销售,妈妈实际花了294元,这条裙子原价是 元。
考点精讲练
考点04 折扣问题
解:294÷60%=490(元)
答:这条裙子原价是490元。
故答案为:490。
【真题强化4-2】(2022秋 婺城区期末)富华商场所有商品都按八五折出售。一部华为手机原价2400元,一盏小米台灯原价150元。刘阿姨带着2500元想买一部华为手机和3盏小米台灯,她带的钱够吗?
考点精讲练
考点04 折扣问题
解:2400+3×150
=2400+450
=2850(元)
2850×85%=2422.5(元)
2422.5<2500
答:她带的钱够。
【典例精讲】(2023春 海城市期中)幸福农场去年产小麦60吨,今年由于气候原因减产二成五,今年产小麦 吨。
考点精讲练
考点05 成数问题
解:60×(1﹣25%)
=60×0.75
=45(吨)
答:今年产小麦45吨。
故答案为:45。
【真题强化5-1】(2023春 路北区期中)某村去年共收获小麦100吨,比前年多收20吨,该村去年小麦产量比前年增加了( )
A.一成五 B.二成 C.二成五 D.三成
考点精讲练
考点05 成数问题
解:60×(1﹣25%)
=60×0.75
=45(吨)
答:今年产小麦45吨。
故答案为:45。
【真题强化5-2】(2020 四子王旗)某景点2019年国庆期间,游客达到约24万人,比去年同期大约增加了4万人,这样比去年同期增加了( )
A.七成五 B.二成五 C.二成
考点精讲练
考点05 成数问题
解:24﹣4=20(万人)
4÷20=20%
20%=二成
答:这样比去年同期增加了二成。
故选:C。
【典例精讲】(2021 行唐县)妈妈存入银行60000元,整存整取一年,年利率是2.52%,一年后妈妈从银行共取回 元.
考点精讲练
考点06 利率问题
解:60000+60000×2.25%×1
=60000+1350
=61350(元)
答:一年后妈妈从银行共取回61350元.
故答案为:61350元.
【真题强化1-1】(2023 讷河市)2022年元旦,妈妈存入银行30000元,整存整取一年期,年利率是2.25%。到期时,妈妈从银行可以取出 元。
考点精讲练
考点06 利率问题
解:30000+30000×1×2.25%
=30000+675
=30675(元)
答:妈妈从银行可以取出30675元。
故答案为:30675。
【真题强化1-2】(2022 延吉市)六年级一班将280元钱存入银行,如果每月的利率是0.1425%,存满半年后可取出多少元钱?
考点精讲练
考点06 利率问题
解:半年=6个月,
280+280×0.1425%×6.
【典例精讲】(2022春 定襄县校级月考)王师傅本月的应纳税所得额是640元,如果按3%的税率缴纳个人所得税 元.
考点精讲练
考点07 税率问题
解:640×3%=640×0.03=19.2(元);
答:缴纳个人所得税19.2元.
故答案为:19.2.
【真题强化7-1】(2023春 宁县期中)2018年10月份起,国家将个人所得税征税起点调至5000元。王叔叔11月份收入8000元,如果应纳税额的税率是3%,那么王叔叔应纳税 元,实际收入 元。
考点精讲练
考点07 税率问题
解:(8000﹣5000)×3%
=3000×3%
=90(元)
8000﹣90=7910(元)
答:王叔叔应纳税90元,实际收入7910元。
故答案为:90,7910。
【真题强化7-2】(2022春 定南县期中)张华写了一本散文集的稿费5000元,按照个人所得税法规定,稿费收入超过800元的部分按20%交纳个人所得税,他应缴税多少元?
考点精讲练
考点07 税率问题
解:(5000﹣800)×20%
=4200×0.2
=840(元)
答:他应缴税840元.
【典例精讲】(2020 阿坝州)某商品按定价的80%(八折)出售,仍能获得20%的利润,定价时期望的利润百分数是( )
A.40% B.60% C.72% D.50%
考点精讲练
考点08 利润率问题
解:设定价是1,那么现价是:
1×80%=0.8
0.8÷(1+20%)
=0.8÷120%
=
(1﹣ )÷
= ÷
=50%
答:定价时期望的利润是50%。
故选:D。
【真题强化8-1】(2023 宝安区模拟)商场举行促销活动,某种手机如果按每台840元售出,可获得利润20%,如果按原价售出,则可获利30%,这种手机在促销活动中降价多少元?
考点精讲练
考点08 利润率问题
解:840÷(1+20%)
=840÷120%
=700(元);
700×(1+30%),
=700×130%,
=910(元);
910﹣840=70(元);
答:该手机的价格在这次的促销活动中降价70元.
【真题强化8-2】(2022 大庆模拟)某书店出售一种挂历,每出售一本可获得利润18元.出售 后,每本减价10元,全部售完,共获利润3000元.这个书店出售这种挂历多少本?
考点精讲练
考点08 利润率问题
解:设书店共出售这种挂历x本,
18× x+(18﹣10)×(1﹣ )x=3000
x+ x=3000
12x=3000
x=250,
答:这个书店出售这种挂历250本.
1.完成讲义真题训练;
2.复习本讲错题。
课后作业
第六单元 百分数
期末考点集训
2023-2024学年苏教版数学六年级上册
知识点01:百分数的意义和读写
1.百分数的意义:表示一个数是另一个数的百分之几的数,百分数又叫作百分比或百分率。
2.百分数的读法:先读百分号(分母),读成“百分之”,再读百分号前面的数(分子)。
3.百分数的写法:百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示。
知识点02:百分数、小数和分数的互化
1. 百分数与小数的互化
(1)小数化成百分数,将它的小数点向右移动两位,同时在末尾添上百分号。
(2)百分数化成小数,小数点向左移动两位,同时去掉百分号。在移动小数点的过程中,如果位数不够,添0补足。
2. 百分数与分数的互化
(1)把分数化成百分数,先把分数化成小数,再把小数化成百分数。
(2)百分数化成分数,先把百分数改写成分母是100的分数,再化成最简分数。
知识解读
知识点03:求百分率的实际问题
1.求一个数是另一个数的百分之几的实际问题
求一个数是另一个数的百分之几的解题方法与求一个数是另一个数的几分之几的解题方法相同,都用除法计算。
2. 求百分率
求百分率就是求一个数是另一个数的百分之几,用除法计算。
3. 求一个数比另一个数多(少)百分之几
(1)求甲数比乙数多百分之几:(甲数-乙数)÷乙数
知识解读
(2)求甲数比乙数多百分之几:甲数÷乙数-1。
(3)求甲数比乙数少百分之几:(乙数-甲数)÷乙数
(4)求甲数比乙数少百分之几:(乙数-甲数)÷乙数
知识解读
知识点04:百分数的实际应用
1.应纳税额的计算方法:求应纳税额就是求一个数的百分之几是多少,用乘法计算:应纳税额=营业额×税率
2.利息的计算方法:求应纳税额就是求一个数的百分之几是多少,用乘法计算:应纳税额=营业额×税率
3. 折扣问题的解法:解决折扣问题,首先看是打几折,打几折就是按原价的百分之几十出售。现价=原价×折扣
知识点05:列方程解应用题
1. 已知部分数占总数的百分之几和另一部分数,求总数
在实际问题中,要找准把哪个数量看做单位“1”,单位“1”未知时,通常设单位“1”为x,先找出题目中的数量关系,再列方程解决问题。
2. 已知一个数比另一个数多百分之几,求另一个数
在列方程解决倍、差问题时,要注意先找准单位“1”的量,通常情况下设单位“1”的量为x,再根据另一个量与单位“1”的量之间的关系,用含有x的式子表示出另一个量,最后根据它们的和或差列出方程求解。
知识解读
易错点01:百分数的认识、互化、合格率
1.写百分数时,要将分母写成百分号“% ”,分子写在百分号前面。
2.百分数表示的是两个数量之间的倍比关系,只表示两个数量之间的关系,既不能表示具体的数量,也不能带单位名称。
3.将整数改写成百分数时,因为添上百分号后,得到的数就缩小到原来的百分之一,所以要先把原数扩大到原来的100倍,才能保证原数的大小不变。
4.将百分数化成小数,去掉百分号后,一定要将小数点向左移动两位,位数不够时,用“0”补足。
5.将分数化成百分数,用分子除以分母,在除不尽保留近似值时应该用“≈”连接,在将近似值化成百分数应该用“=”连接。
易错点02:百分率及其应用
1.求百分率实质上是求一个数是另一个数的百分之几,只是在计算时要乘100%,把结果化成百分数。
2.及格率、合格率、命中率、出勤率、成活率、出粉率都不能大于100%。
3.“降低了”是指原有数量中减少的部分;“降低到”是指从原有数量中减去一部分后得到的数量。
易错点03:税率利率折扣问题
1.任何一种存款,在计算利息时,都要乘存入时间。
2.商品打折后,比原价降低的金额=原价-现价。
3.解决有关百分数的实际问题,在找准单位“1”的同时,还要看清所要求的问题与单位“1”的关系。
易错点拨
【考点01】百分数的意义、读写及应用
【考点02】小数、分数和百分数之间的关系及其转化
【考点03】增长率变化率问题
【考点04】折扣问题
【考点05】成数问题
【考点06】利率问题
【考点07】税率问题
【考点08】利润率问题
考点目录
【典例精讲】(2022秋 罗湖区期中)看图,在括号里填上百分数,在方框里填上分数。
考点精讲练
考点01 百分数的意义、读写及应用
解:括号里面的数是:
【真题强化1-1】(2023 洛龙区)下列事件中的百分率可能大于100%的是( )
A.栽种120棵树的成活率
B.六一班学生参加书法比赛的获奖率
C.小麦的出粉率
D.2023年某超市营业额的增长率
考点精讲练
考点01 百分数的意义、读写及应用
解:因为超市营业额可能超过去年的,因此某超市今年的销售额是去年的百分之几可能大于100%。成活率和获奖率最高是100%,出粉率不能达到100%。
故选:D。
【真题强化1-2】(2022秋 三河市期末)我们可以用很多方式描述两个数之间的关系,除了用大于、小于、等于、多和少之外,还可以用倍、分数、比和百分数描述数之间的关系。如果将2、3、5、6、8分别和4进行比较,我们可以说2是4的 %,3是4的,5比4多 ,6和4的比为( : ),
8是4的 倍。
考点精讲练
考点01 百分数的意义、读写及应用
解:2÷4 3÷4= (5﹣1)÷4
=0.5 6:4=3:2
=50% 8÷4=2
=1÷4
=
答:2是4的50%,3是4的 ,5比4多 ,6和4的比为3:2,8是4的2倍。
故答案为:50; ; ;3,2;2。
【典例精讲】(2023 都江堰市)0.75里面有 个0.01
2:5= = %= (填小数)
考点精讲练
考点02 小数、分数和百分数之间的关系及其转化
解:0.75里面有75个0.01
2:5= =40%=0.4
故答案为:75,40,0.4。
【真题强化2-1】(2023 都江堰市)0.75里面有 个0.01
2:5= = %= (填小数)
考点精讲练
考点02 小数、分数和百分数之间的关系及其转化
解:0.75里面有75个0.01
2:5= =40%=0.4
故答案为:75,40,0.4。
【真题强化2-2】(2023 陆丰市)一个数由5个十分之一和3个百分之一组成,这个数写成小数是 ,写成分数是 ,写成百分数是 。
考点精讲练
考点02 小数、分数和百分数之间的关系及其转化
解:一个数由5个十分之一和3个百分之一组成,这个数写成小数是0.53,写成分数是 ,写成百分数是53%。
故答案为:0.53; ;53%。
【典例精讲】(2023春 义乌市期末)五一期间,商场促销,所有商品一律九折出售。九折是指 是
的 ;某商品原价是320元,打折后卖是 元。
考点精讲练
考点03 增长率变化率问题
解:九折是指售价(或现价)是原价的 ;
320× =288(元)。
故答案为:售价(或现价),原价,288。
【真题强化3-1】(2023 通河县)“低碳生活,绿色出行”,广州2010年亚运会后,许多地方增设路边绿化带,自行车道也有增加,不少市民喜欢骑单车出行,享受绿色环保的出行方式。自行车正逐渐成为人们喜爱的交通工具。某商城的自行车销售量自2016年起逐月增加。据统计,该商城1月份销售自行车75辆,2月份销售自行车90辆。若该商城前4个月自行车销量的月平均增长率相同,则该商城3月份销售多少辆自行车?
考点精讲练
考点03 增长率变化率问题
解:设该商城前4个月自行车销量的月平均增长率位为x,根据题意可得:
75×(1+x)=90
75×(1+x)÷75=90÷75
1+x=1.2
1+x﹣1=1.2﹣1
x=0.2
90×(1+0.2)
=90×1.2
=108(辆) 答:该商城3月份销售108辆自行车。
【真题强化3-2】(2023 安宁区)张村有一块试验田种水稻,今年换种新品种后,产量是2600千克,今年产量比去年增产三成,去年的产量是多少千克?
考点精讲练
考点03 增长率变化率问题
解:2600÷(1+30%)
=2600÷1.3
=2000(千克)
答:去年的产量是2000千克。
【典例精讲】(2020 魏县)某商场五一期间举行优惠销售活动,采取“满一百元送二十元,并且连环赠送”的酬宾方式,即顾客每消费满100元(100元可以是现金,也可以是购物券,或二者合计)就送20元购物券,满200元就送40元购物券,依此类推,现有一位顾客第一次就用了16000元购物,并用所得购物券继续购物,那么他购回的商品大约相当于它们原价的( )
A.75% B.80% C.85% D.90%
考点精讲练
考点04 折扣问题
解:根据题意:这位顾客付的钱数是16 000元;
这位顾客所购买的商品的价值是16000元,赠送的购物券的金额是16000× =3200元,3200元赠送的购物券是:3200×20%=640元,640元赠送的购物券是600× =120元,再送购物券20元,
因而用16000元购买的商品的价值是16000+3200+640+120+20=19980元.因而可以设他购回的商品大约相当于它们原价的百分比是x.
则得方程:19980x=16000,
解得:x≈0.8=80%.
故选:B。
【真题强化4-1】(2022秋 泗洪县期末)妈妈买一条裙子,商场促销打六折销售,妈妈实际花了294元,这条裙子原价是 元。
考点精讲练
考点04 折扣问题
解:294÷60%=490(元)
答:这条裙子原价是490元。
故答案为:490。
【真题强化4-2】(2022秋 婺城区期末)富华商场所有商品都按八五折出售。一部华为手机原价2400元,一盏小米台灯原价150元。刘阿姨带着2500元想买一部华为手机和3盏小米台灯,她带的钱够吗?
考点精讲练
考点04 折扣问题
解:2400+3×150
=2400+450
=2850(元)
2850×85%=2422.5(元)
2422.5<2500
答:她带的钱够。
【典例精讲】(2023春 海城市期中)幸福农场去年产小麦60吨,今年由于气候原因减产二成五,今年产小麦 吨。
考点精讲练
考点05 成数问题
解:60×(1﹣25%)
=60×0.75
=45(吨)
答:今年产小麦45吨。
故答案为:45。
【真题强化5-1】(2023春 路北区期中)某村去年共收获小麦100吨,比前年多收20吨,该村去年小麦产量比前年增加了( )
A.一成五 B.二成 C.二成五 D.三成
考点精讲练
考点05 成数问题
解:60×(1﹣25%)
=60×0.75
=45(吨)
答:今年产小麦45吨。
故答案为:45。
【真题强化5-2】(2020 四子王旗)某景点2019年国庆期间,游客达到约24万人,比去年同期大约增加了4万人,这样比去年同期增加了( )
A.七成五 B.二成五 C.二成
考点精讲练
考点05 成数问题
解:24﹣4=20(万人)
4÷20=20%
20%=二成
答:这样比去年同期增加了二成。
故选:C。
【典例精讲】(2021 行唐县)妈妈存入银行60000元,整存整取一年,年利率是2.52%,一年后妈妈从银行共取回 元.
考点精讲练
考点06 利率问题
解:60000+60000×2.25%×1
=60000+1350
=61350(元)
答:一年后妈妈从银行共取回61350元.
故答案为:61350元.
【真题强化1-1】(2023 讷河市)2022年元旦,妈妈存入银行30000元,整存整取一年期,年利率是2.25%。到期时,妈妈从银行可以取出 元。
考点精讲练
考点06 利率问题
解:30000+30000×1×2.25%
=30000+675
=30675(元)
答:妈妈从银行可以取出30675元。
故答案为:30675。
【真题强化1-2】(2022 延吉市)六年级一班将280元钱存入银行,如果每月的利率是0.1425%,存满半年后可取出多少元钱?
考点精讲练
考点06 利率问题
解:半年=6个月,
280+280×0.1425%×6.
【典例精讲】(2022春 定襄县校级月考)王师傅本月的应纳税所得额是640元,如果按3%的税率缴纳个人所得税 元.
考点精讲练
考点07 税率问题
解:640×3%=640×0.03=19.2(元);
答:缴纳个人所得税19.2元.
故答案为:19.2.
【真题强化7-1】(2023春 宁县期中)2018年10月份起,国家将个人所得税征税起点调至5000元。王叔叔11月份收入8000元,如果应纳税额的税率是3%,那么王叔叔应纳税 元,实际收入 元。
考点精讲练
考点07 税率问题
解:(8000﹣5000)×3%
=3000×3%
=90(元)
8000﹣90=7910(元)
答:王叔叔应纳税90元,实际收入7910元。
故答案为:90,7910。
【真题强化7-2】(2022春 定南县期中)张华写了一本散文集的稿费5000元,按照个人所得税法规定,稿费收入超过800元的部分按20%交纳个人所得税,他应缴税多少元?
考点精讲练
考点07 税率问题
解:(5000﹣800)×20%
=4200×0.2
=840(元)
答:他应缴税840元.
【典例精讲】(2020 阿坝州)某商品按定价的80%(八折)出售,仍能获得20%的利润,定价时期望的利润百分数是( )
A.40% B.60% C.72% D.50%
考点精讲练
考点08 利润率问题
解:设定价是1,那么现价是:
1×80%=0.8
0.8÷(1+20%)
=0.8÷120%
=
(1﹣ )÷
= ÷
=50%
答:定价时期望的利润是50%。
故选:D。
【真题强化8-1】(2023 宝安区模拟)商场举行促销活动,某种手机如果按每台840元售出,可获得利润20%,如果按原价售出,则可获利30%,这种手机在促销活动中降价多少元?
考点精讲练
考点08 利润率问题
解:840÷(1+20%)
=840÷120%
=700(元);
700×(1+30%),
=700×130%,
=910(元);
910﹣840=70(元);
答:该手机的价格在这次的促销活动中降价70元.
【真题强化8-2】(2022 大庆模拟)某书店出售一种挂历,每出售一本可获得利润18元.出售 后,每本减价10元,全部售完,共获利润3000元.这个书店出售这种挂历多少本?
考点精讲练
考点08 利润率问题
解:设书店共出售这种挂历x本,
18× x+(18﹣10)×(1﹣ )x=3000
x+ x=3000
12x=3000
x=250,
答:这个书店出售这种挂历250本.
1.完成讲义真题训练;
2.复习本讲错题。
课后作业
