3.1 图形的平移(第2课时)同步课件(共21张PPT)
文档属性
| 名称 | 3.1 图形的平移(第2课时)同步课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:47 | ||
图片预览



文档简介
(共21张PPT)
3.1 图形的平移
(第二课时)
素养目标
技能目标
知识目标
在同一直角坐标系中,感受图形上点的坐标变化与图形的平移之间的关系。
经历图形的平移与图形坐标的变化之间关系的探索过程,发展学生的形象思维和数形结合的意识。
通过对比新旧图形对应点坐标的变化,培养学生的观察、分析、归纳的能力,从而获得分析问题、解决问题的能力。
教学重点
教学难点
进一步理解平移的特征,探索图形的平移与点的坐标之间的关系。
由坐标的变化探索新旧图形之间的变化。
思考1:平移的定义.
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
思考2:平移的性质.
(1)对应点所连的线段平行且相等;
(2)对应线段平行且相等;
(3)对应角相等;
(4)图形的形状和大小不改变。
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
平面直角坐标系中点的平移
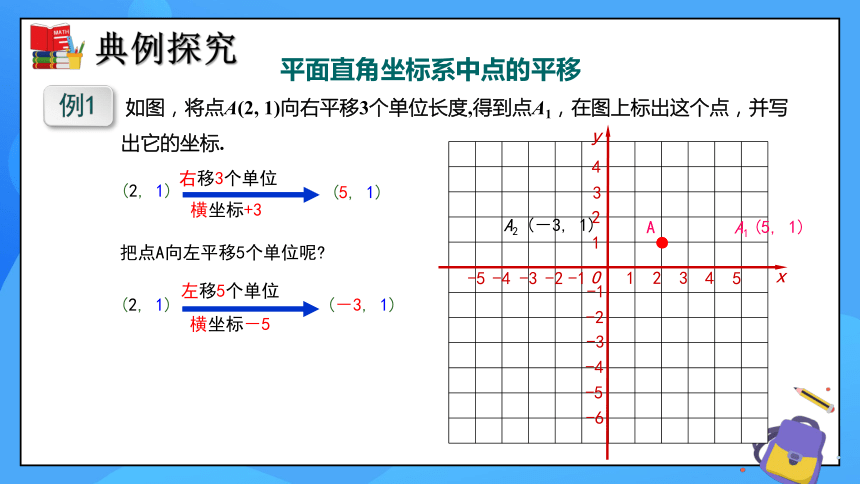
如图,将点A(2, 1)向右平移3个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移5个单位呢
A1
(5, 1)
A
(-3, 1)
A2
(2, 1)
右移3个单位
(5, 1)
横坐标+3
(2, 1)
左移5个单位
(-3, 1)
横坐标-5
例1
x
向左平移m个单位对应点为(x-m,y)
你能总结出点(x,y)
的平移规律吗?
向右平移m个单位对应点为(x+m,y)
那我们可以记为“左减右加”
将点A(-2,3)向左平移3个单位长度,得到对应点坐标是 。
1.
(-5,3)
将点A(5,-4)向右平移2个单位长度,得到对应点坐标是 。
(7,-4)
平面直角坐标系中图形的平移
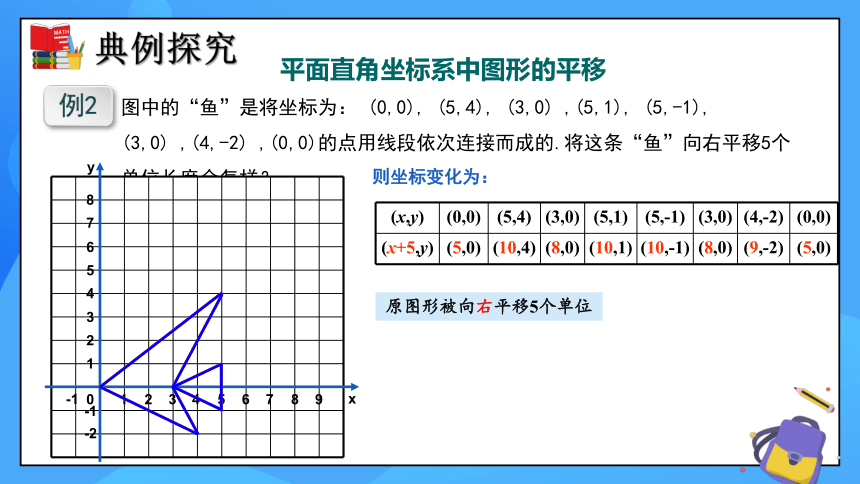
图中的“鱼”是将坐标为: (0,0), (5,4), (3,0) ,(5,1), (5,-1), (3,0) ,(4,-2) ,(0,0)的点用线段依次连接而成的.将这条“鱼”向右平移5个单位长度会怎样?
例2
0
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
-1
-2
-1
y
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x+5,y) (5,0) (10,4) (8,0) (10,1) (10,-1) (8,0) (9,-2) (5,0)
原图形被向右平移5个单位
平面直角坐标系中图形的平移
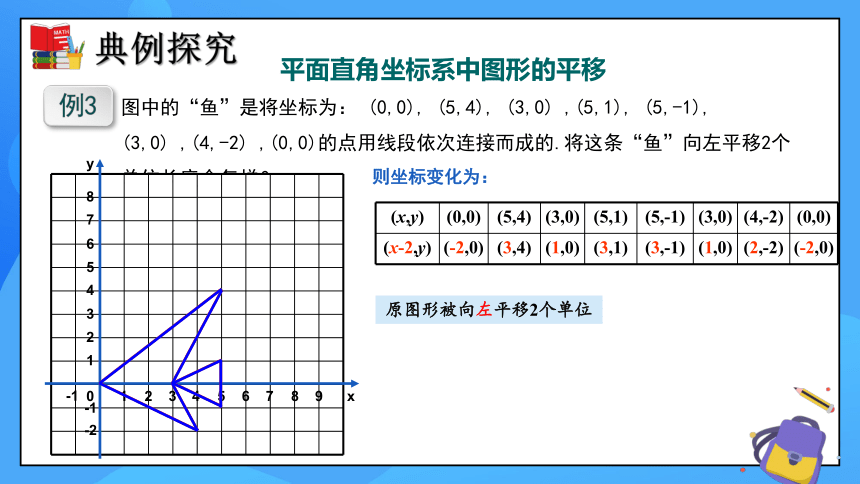
图中的“鱼”是将坐标为: (0,0), (5,4), (3,0) ,(5,1), (5,-1), (3,0) ,(4,-2) ,(0,0)的点用线段依次连接而成的.将这条“鱼”向左平移2个单位长度会怎样?
例3
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x-2,y) (-2,0) (3,4) (1,0) (3,1) (3,-1) (1,0) (2,-2) (-2,0)
原图形被向左平移2个单位
0
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
y
-1
-2
-1
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
平面直角坐标系中点的平移
如图,将点A(2, 1)向上平移3个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移5个单位呢
A1
(2, 4)
A
(2, -4)
A2
(2, 1)
上移3个单位
(2, 4)
纵坐标y+3
(2, 1)
下移5个单位
(2, -4)
纵坐标y-5
例1
x
(2, 1)
向下平移n个单位对应点为(x,y-n)
你能总结出点(x,y)
的平移规律吗?
向上平移n个单位对应点为(x,y+n)
那我们可以记为“上加下减”
将点A(-2,3)向上平移3个单位长度,得到对应点坐标是 。
1.
(-2,6)
将点A(5,-4)向下平移2个单位长度,得到对应点坐标是 。
(5,-6)
平面直角坐标系中图形的平移
图中的“鱼”是将坐标为: (0,0), (5,4), (3,0) ,(5,1), (5,-1), (3,0) ,(4,-2) ,(0,0)的点用线段依次连接而成的.将这条“鱼”向上平移3个单位长度会怎样?
例4
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,y+3) (0,3) (5,7) (3,3) (5,4) (5,2) (3,3) (4,1) (0,3)
原图形被向上平移3个单位
0
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
y
-1
-2
-1
平面直角坐标系中图形的平移
图中的“鱼”是将坐标为: (0,0), (5,4), (3,0) ,(5,1), (5,-1), (3,0) ,(4,-2) ,(0,0)的点用线段依次连接而成的.将这条“鱼”向上平移3个单位长度会怎样?
例5
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,y-2) (0,-2) (5,2) (3,-2) (5,-1) (5,-3) (3,-2) (4,-4) (0,-2)
原图形被向下平移2个单位
0
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
y
-1
-2
-1
-3
-4
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
1.
线段CD是由线段AB平移得到的.其中点A(–1,4)的对应点为C(4,4),则点B(–4,–1)的对应点D的坐标为___________.
2.
(1,-1)
将坐标作如下变化时,图形将怎样变化?
3.
①. (x,y) (x,y+4) ②.(x,y) (x-4,y)
③. (x,y) (x,y-2) ④.(x,y) (x+2,y)
向上平移4个单位长度
向左平移4个单位长度
向下平移2个单位长度
向右平移2个单位长度
如图,在平面直角坐标系中,平移△ABC后,点A的对应点A′的坐标为(-3,-2),则点B的对应点B′的坐标为( )
4.
C
A.(2,1)
B.(2,2)
C.(1,0)
D.(1,3)
(x , y)
思想方法
逆向思维,转化思维。
文字语言-图形语言-符号语言的互相转化.
数形结合思想,数学建模.
图形在坐标系中的平移
向右平移m个单位
(x+m , y)
向左平移m个单位
(x-m , y)
(x , y)
向上平移n个单位
(x , y+n)
向下平移n个单位
(x , y+n)
上加下减
右加左减
习题3.2第1、3题
3.1 图形的平移
(第二课时)
素养目标
技能目标
知识目标
在同一直角坐标系中,感受图形上点的坐标变化与图形的平移之间的关系。
经历图形的平移与图形坐标的变化之间关系的探索过程,发展学生的形象思维和数形结合的意识。
通过对比新旧图形对应点坐标的变化,培养学生的观察、分析、归纳的能力,从而获得分析问题、解决问题的能力。
教学重点
教学难点
进一步理解平移的特征,探索图形的平移与点的坐标之间的关系。
由坐标的变化探索新旧图形之间的变化。
思考1:平移的定义.
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
思考2:平移的性质.
(1)对应点所连的线段平行且相等;
(2)对应线段平行且相等;
(3)对应角相等;
(4)图形的形状和大小不改变。
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
平面直角坐标系中点的平移
如图,将点A(2, 1)向右平移3个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移5个单位呢
A1
(5, 1)
A
(-3, 1)
A2
(2, 1)
右移3个单位
(5, 1)
横坐标+3
(2, 1)
左移5个单位
(-3, 1)
横坐标-5
例1
x
向左平移m个单位对应点为(x-m,y)
你能总结出点(x,y)
的平移规律吗?
向右平移m个单位对应点为(x+m,y)
那我们可以记为“左减右加”
将点A(-2,3)向左平移3个单位长度,得到对应点坐标是 。
1.
(-5,3)
将点A(5,-4)向右平移2个单位长度,得到对应点坐标是 。
(7,-4)
平面直角坐标系中图形的平移
图中的“鱼”是将坐标为: (0,0), (5,4), (3,0) ,(5,1), (5,-1), (3,0) ,(4,-2) ,(0,0)的点用线段依次连接而成的.将这条“鱼”向右平移5个单位长度会怎样?
例2
0
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
-1
-2
-1
y
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x+5,y) (5,0) (10,4) (8,0) (10,1) (10,-1) (8,0) (9,-2) (5,0)
原图形被向右平移5个单位
平面直角坐标系中图形的平移
图中的“鱼”是将坐标为: (0,0), (5,4), (3,0) ,(5,1), (5,-1), (3,0) ,(4,-2) ,(0,0)的点用线段依次连接而成的.将这条“鱼”向左平移2个单位长度会怎样?
例3
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x-2,y) (-2,0) (3,4) (1,0) (3,1) (3,-1) (1,0) (2,-2) (-2,0)
原图形被向左平移2个单位
0
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
y
-1
-2
-1
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
平面直角坐标系中点的平移
如图,将点A(2, 1)向上平移3个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移5个单位呢
A1
(2, 4)
A
(2, -4)
A2
(2, 1)
上移3个单位
(2, 4)
纵坐标y+3
(2, 1)
下移5个单位
(2, -4)
纵坐标y-5
例1
x
(2, 1)
向下平移n个单位对应点为(x,y-n)
你能总结出点(x,y)
的平移规律吗?
向上平移n个单位对应点为(x,y+n)
那我们可以记为“上加下减”
将点A(-2,3)向上平移3个单位长度,得到对应点坐标是 。
1.
(-2,6)
将点A(5,-4)向下平移2个单位长度,得到对应点坐标是 。
(5,-6)
平面直角坐标系中图形的平移
图中的“鱼”是将坐标为: (0,0), (5,4), (3,0) ,(5,1), (5,-1), (3,0) ,(4,-2) ,(0,0)的点用线段依次连接而成的.将这条“鱼”向上平移3个单位长度会怎样?
例4
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,y+3) (0,3) (5,7) (3,3) (5,4) (5,2) (3,3) (4,1) (0,3)
原图形被向上平移3个单位
0
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
y
-1
-2
-1
平面直角坐标系中图形的平移
图中的“鱼”是将坐标为: (0,0), (5,4), (3,0) ,(5,1), (5,-1), (3,0) ,(4,-2) ,(0,0)的点用线段依次连接而成的.将这条“鱼”向上平移3个单位长度会怎样?
例5
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,y-2) (0,-2) (5,2) (3,-2) (5,-1) (5,-3) (3,-2) (4,-4) (0,-2)
原图形被向下平移2个单位
0
1
2
3
4
5
6
7
8
9
x
1
2
3
4
5
6
7
8
y
-1
-2
-1
-3
-4
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
1.
线段CD是由线段AB平移得到的.其中点A(–1,4)的对应点为C(4,4),则点B(–4,–1)的对应点D的坐标为___________.
2.
(1,-1)
将坐标作如下变化时,图形将怎样变化?
3.
①. (x,y) (x,y+4) ②.(x,y) (x-4,y)
③. (x,y) (x,y-2) ④.(x,y) (x+2,y)
向上平移4个单位长度
向左平移4个单位长度
向下平移2个单位长度
向右平移2个单位长度
如图,在平面直角坐标系中,平移△ABC后,点A的对应点A′的坐标为(-3,-2),则点B的对应点B′的坐标为( )
4.
C
A.(2,1)
B.(2,2)
C.(1,0)
D.(1,3)
(x , y)
思想方法
逆向思维,转化思维。
文字语言-图形语言-符号语言的互相转化.
数形结合思想,数学建模.
图形在坐标系中的平移
向右平移m个单位
(x+m , y)
向左平移m个单位
(x-m , y)
(x , y)
向上平移n个单位
(x , y+n)
向下平移n个单位
(x , y+n)
上加下减
右加左减
习题3.2第1、3题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
