3.2 图形的旋转(第2课时)同步课件(共21张PPT)
文档属性
| 名称 | 3.2 图形的旋转(第2课时)同步课件(共21张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览





文档简介
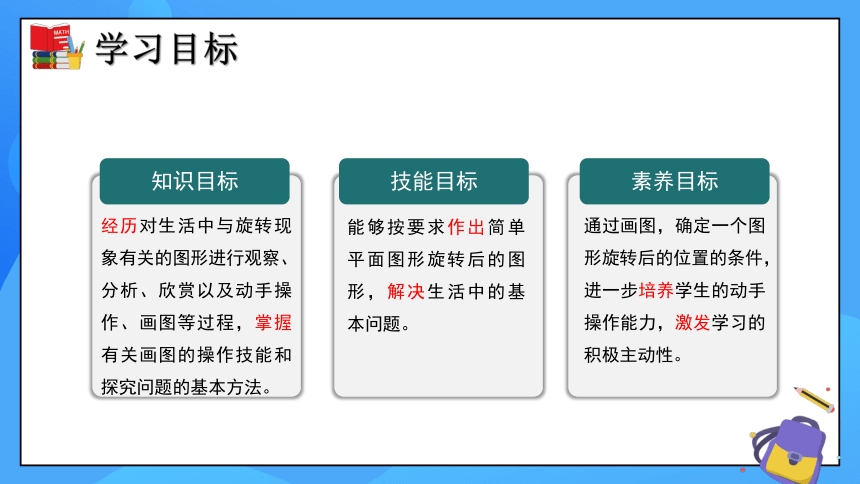
(共21张PPT)
3.2 图形的旋转
(第二课时)
素养目标
技能目标
知识目标
经历对生活中与旋转现象有关的图形进行观察、分析、欣赏以及动手操作、画图等过程,掌握有关画图的操作技能和探究问题的基本方法。
能够按要求作出简单平面图形旋转后的图形,解决生活中的基本问题。
通过画图,确定一个图形旋转后的位置的条件,进一步培养学生的动手操作能力,激发学习的积极主动性。
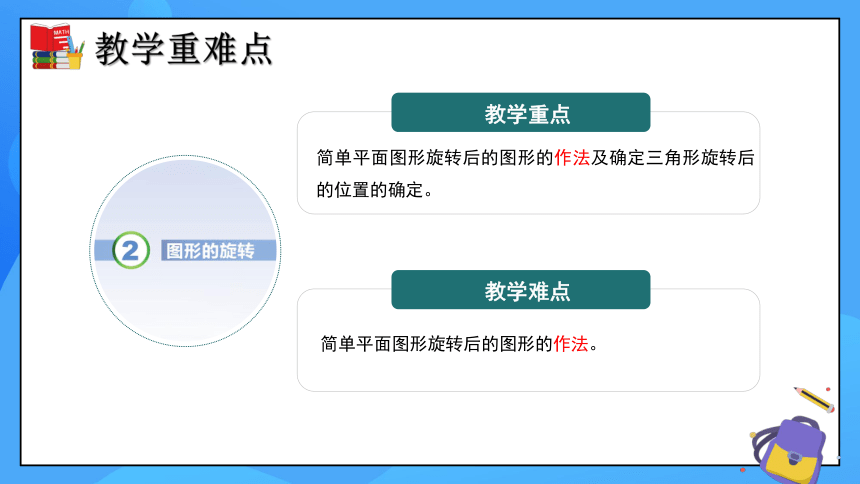
教学重点
教学难点
简单平面图形旋转后的图形的作法及确定三角形旋转后的位置的确定。
简单平面图形旋转后的图形的作法。
思考1:
平移的基本性质是什么?
3.对应角 .
1.平移的两个图形 .
2.对应线段平行(或在同一直线上且) .
4.对应点所连的线段 .
全等
相等
相等
平行且相等
思考2:
旋转的基本性质是什么?
3.旋转前、后的图形 .
1.对应点到旋转中心的距离 .
2.对应点与旋转中心所连线段的夹角等于 .
4.图形的旋转是由 和旋转的决定.
相等
旋转角
全等
旋转中心
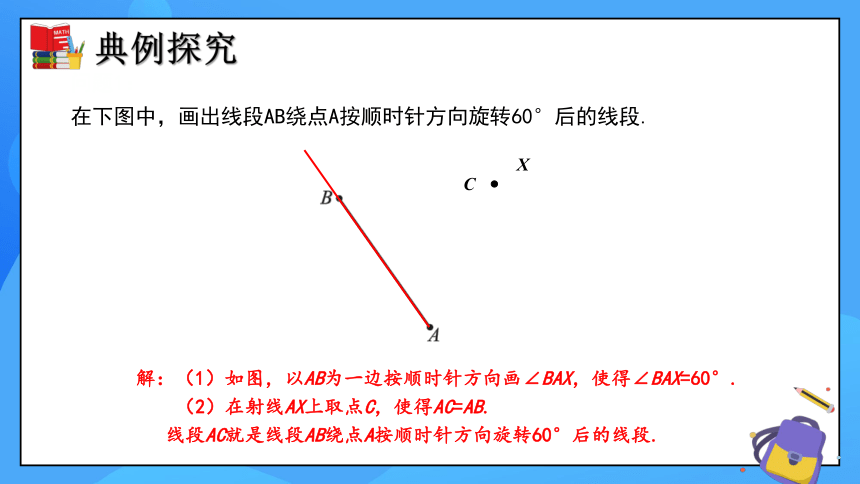
问题1:
在下图中,画出线段AB绕点A按顺时针方向旋转60°后的线段.
解:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.
线段AC就是线段AB绕点A按顺时针方向旋转60°后的线段.
X
C
问题2:
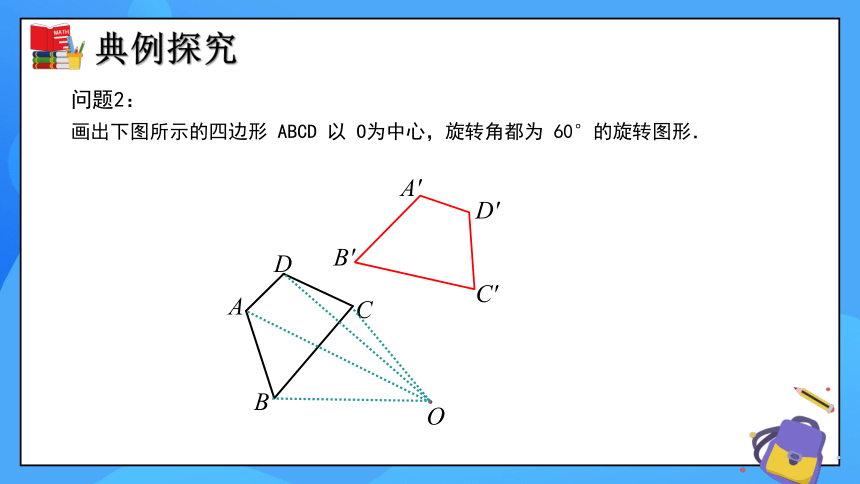
画出下图所示的四边形 ABCD 以 O为中心,旋转角都为 60°的旋转图形.
A
B
C
D
O
B'
A'
C'
D'
你能否描述一下旋转作图的一般步骤吗?
1.定:确定旋转中心、旋转方向及旋转角.
2.找:找出构成图形的关键点.
3.旋:沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点.
4.连:顺次连接各个关键的对应点,并标上相应字母.
5.写:根据作图要求写出所作的图形.
你能否描述一下确定旋转中心与旋转角的方法吗?
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是不在图形上;
①若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;
②若不在图形上,对应点连线的垂直平分线的交点就是旋转中心,旋转角等于对应点与旋转中心所连线段的夹角.
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换 运动方向 运动量的衡量
平移
旋转
平移和旋转的异同:
直线
移动一定距离
顺时针或逆时针
转动一定的角度
例1
怎样将甲图案变成乙图案?
甲
A
B
可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案
例1
怎样将甲图案变成乙图案?
甲
乙
B
A
可以先将甲图案沿AB方向平移到B点位置,再将所得图案绕图上的B点旋转,使得图案被“扶直”,然后,即可得到乙图案
还可以用什么方法把甲图案变成乙图案?
例2
如图所示,怎样将右边的图案变成左边的图案?
答:以右边图案的中心为旋转中心,将图案按逆时针方向旋转90°,
然后平移,即可得到左边的图案.
例3
如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
解:(1)连接OA、OB、OC、OD、OE;
(2)分别以OB、OC、OD为一边作∠BOF, ∠COG, ∠DOH,使∠BOF= ∠COG= ∠DOH= ∠AOE;
(3)分别在射线OF,OG,OH上,截取OF=OB,OG=OC,OH=OD;
(4)连接EF,FG,GH,HE,
四边形EFGH就是四边形ABCD绕O点旋转后的图形.
1.
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么点A(-2,5)的对应点A′的坐标是________.
(5,2)
2.
下列关于旋转和平移的说法正确的是( )
A.旋转使图形的形状发生改变
B.由旋转得到的图形一定可以通过平移得到
C.平移与旋转的共同之处是改变图形的位置和大小
D.对应点到旋转中心距离相等
D
3.
如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点D
顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CD的
中点O旋转180°.
4.
小明和妈妈在广场游玩时, 看见许多喷水嘴正在给草坪浇水。 喷水嘴不停地旋转着, 但每时每刻喷出的水雾总是四分之一圆。妈妈问:“小明,如果喷出水雾的范围内有一正方形, 喷水嘴位于它的中心, 你知道喷水嘴在旋转的过程中瞬时浇过正方形区域的面积是多少吗 ”
同学们,请你替小明做出回答。
O
A
B
C
D
E
F
作旋转图形步骤:
1.定:确定旋转中心、旋转方向及旋转角.
2.找:找出构成图形的关键点.
3.旋:沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点.
4.连:顺次连接各个关键的对应点,并标上相应字母.
5.写:根据作图要求写出所作的图形.
思想方法
逆向思维,转化思维。
文字语言-图形语言-符号语言的互相转化.
数形结合思想,数学建模.
旋转的作图
习题3.5第1、2题
3.2 图形的旋转
(第二课时)
素养目标
技能目标
知识目标
经历对生活中与旋转现象有关的图形进行观察、分析、欣赏以及动手操作、画图等过程,掌握有关画图的操作技能和探究问题的基本方法。
能够按要求作出简单平面图形旋转后的图形,解决生活中的基本问题。
通过画图,确定一个图形旋转后的位置的条件,进一步培养学生的动手操作能力,激发学习的积极主动性。
教学重点
教学难点
简单平面图形旋转后的图形的作法及确定三角形旋转后的位置的确定。
简单平面图形旋转后的图形的作法。
思考1:
平移的基本性质是什么?
3.对应角 .
1.平移的两个图形 .
2.对应线段平行(或在同一直线上且) .
4.对应点所连的线段 .
全等
相等
相等
平行且相等
思考2:
旋转的基本性质是什么?
3.旋转前、后的图形 .
1.对应点到旋转中心的距离 .
2.对应点与旋转中心所连线段的夹角等于 .
4.图形的旋转是由 和旋转的决定.
相等
旋转角
全等
旋转中心
问题1:
在下图中,画出线段AB绕点A按顺时针方向旋转60°后的线段.
解:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.
线段AC就是线段AB绕点A按顺时针方向旋转60°后的线段.
X
C
问题2:
画出下图所示的四边形 ABCD 以 O为中心,旋转角都为 60°的旋转图形.
A
B
C
D
O
B'
A'
C'
D'
你能否描述一下旋转作图的一般步骤吗?
1.定:确定旋转中心、旋转方向及旋转角.
2.找:找出构成图形的关键点.
3.旋:沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点.
4.连:顺次连接各个关键的对应点,并标上相应字母.
5.写:根据作图要求写出所作的图形.
你能否描述一下确定旋转中心与旋转角的方法吗?
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是不在图形上;
①若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;
②若不在图形上,对应点连线的垂直平分线的交点就是旋转中心,旋转角等于对应点与旋转中心所连线段的夹角.
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换 运动方向 运动量的衡量
平移
旋转
平移和旋转的异同:
直线
移动一定距离
顺时针或逆时针
转动一定的角度
例1
怎样将甲图案变成乙图案?
甲
A
B
可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案
例1
怎样将甲图案变成乙图案?
甲
乙
B
A
可以先将甲图案沿AB方向平移到B点位置,再将所得图案绕图上的B点旋转,使得图案被“扶直”,然后,即可得到乙图案
还可以用什么方法把甲图案变成乙图案?
例2
如图所示,怎样将右边的图案变成左边的图案?
答:以右边图案的中心为旋转中心,将图案按逆时针方向旋转90°,
然后平移,即可得到左边的图案.
例3
如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
解:(1)连接OA、OB、OC、OD、OE;
(2)分别以OB、OC、OD为一边作∠BOF, ∠COG, ∠DOH,使∠BOF= ∠COG= ∠DOH= ∠AOE;
(3)分别在射线OF,OG,OH上,截取OF=OB,OG=OC,OH=OD;
(4)连接EF,FG,GH,HE,
四边形EFGH就是四边形ABCD绕O点旋转后的图形.
1.
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么点A(-2,5)的对应点A′的坐标是________.
(5,2)
2.
下列关于旋转和平移的说法正确的是( )
A.旋转使图形的形状发生改变
B.由旋转得到的图形一定可以通过平移得到
C.平移与旋转的共同之处是改变图形的位置和大小
D.对应点到旋转中心距离相等
D
3.
如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点D
顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CD的
中点O旋转180°.
4.
小明和妈妈在广场游玩时, 看见许多喷水嘴正在给草坪浇水。 喷水嘴不停地旋转着, 但每时每刻喷出的水雾总是四分之一圆。妈妈问:“小明,如果喷出水雾的范围内有一正方形, 喷水嘴位于它的中心, 你知道喷水嘴在旋转的过程中瞬时浇过正方形区域的面积是多少吗 ”
同学们,请你替小明做出回答。
O
A
B
C
D
E
F
作旋转图形步骤:
1.定:确定旋转中心、旋转方向及旋转角.
2.找:找出构成图形的关键点.
3.旋:沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点.
4.连:顺次连接各个关键的对应点,并标上相应字母.
5.写:根据作图要求写出所作的图形.
思想方法
逆向思维,转化思维。
文字语言-图形语言-符号语言的互相转化.
数形结合思想,数学建模.
旋转的作图
习题3.5第1、2题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
