分式方程(课件)-2024年中考数学一轮复习讲练测(全国通用)(39张ppt)
文档属性
| 名称 | 分式方程(课件)-2024年中考数学一轮复习讲练测(全国通用)(39张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 00:00:00 | ||
图片预览










文档简介
(共39张PPT)
第06讲 分式方程
2024年中考数学一轮复习讲练测
目录
CONTENTS
01
02
知识建构
03
考点精讲
考情分析
第一部分
考情分析
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
考点要求 新课标要求 命题预测
解分式方程 能解可化为一元一次方程的分式方程 中考中本考点考查内容以分式方程解法、分式方程含参问题、分式方程的应用题为主,既有单独考查,也有和一次函数、二次函数结合考察,年年考查,分值为10分左右.预计2024年各地中考还将继续考查分式方程解法、分式方程含参问题(较难)、分式方程的应用题,为避免丢分,学生应扎实掌握.
分式方程的应用 能根据具体问题的实际意义,检验方程解的合理性
第二部分
知识建构
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
第三部分
考点精讲
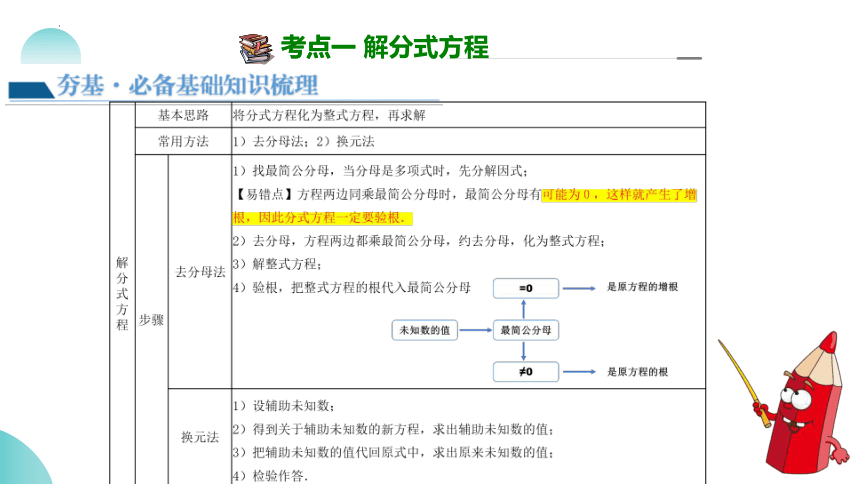
考点一 解分式方程
分式方程的概念:分母中含有未知数的方程叫做分式方程.
增根的概念:在方程变形时,有时可能产生不适合原方程的根,这种根叫做方程的增根.
考点一
考点一 解分式方程
02
考点一
易混易错
考点一 解分式方程
1. 分式方程与整式方程的根本区别:分母中含有未知数,也是判断分式方程的依据.
2. 去分母时要把方程两边的式子作为一个整体,记得不要漏乘整式项.
3. 分式方程的结果还要代回方程的最简公分母中,只有最简公分母不是零的解才是原方程的解.
4. 分式方程的增根是去分母后的整式方程的根,也是使分式方程的公分母为0的根,它不是原分式方程的根.
5. 解分式方程可能产生使分式方程无意义的根,检验是解分式方程的必要步骤.
6. 分式方程有增根与无解并非是同一个概念.分式方程无解,需分类讨论:可能是解为增根,也可能是去分母后的整式方程无解.
【例1】(2021·河南信阳·河南省淮滨县第一中学校考模拟预测)下列方程:①;②;③;④(为已知数),其中分式方程有( )
A.个 B.个 C.个 D.个
【对点训练1】(2022 南明区 二模)下列关于的方程,是分式方程的是( )
A. B. C. D.
02
考点一 解分式方程
题型01 判断分式方程
【例2】(2023·辽宁大连·统考中考真题)将方程去分母,两边同乘后的式子为( )
A. B.
C. D.
【对点训练1】(2023·内蒙古赤峰·统考中考真题)方程的解为 .
【对点训练2】(2022·山东济南·统考中考真题)代数式与代数式的值相等,则x= .
【对点训练3】(2022·湖南常德·统考中考真题)方程的解为 .
02
考点一 解分式方程
题型02 分式方程的一般解法
x=4
7
x=4
02
方法技巧
考点一 解分式方程
解分式方程方法:
先通过方程两边同乘最简公分母将分式方程化为整式方程,再解整式方程,最后需要检验整式方程的解是不是分式方程的解.
02
考点一 解分式方程
题型03 分式方程的特殊解法
类型一 分组通分法
方法简介:如果整个方程一起通分,计算量大又易出错,观察方程中分母的特点可联想分组通分求解.
【例3】解方程:
【详解】解:原方程可变形为,
当5-x≠0时,解得x1=
当5-x=0时,解得x2=
经检验,x1=x2=都是原方程得解.
02
考点一 解分式方程
题型03 分式方程的特殊解法
类型二 分离分式法
方法简介:每个分式的分母与分子相差1,利用这个特点可采用分类分式法求解.
【例4】解方程:
解:原方程可变形为,,
化简得,,即,
∴2x+5=0,解得,x=,
检验,把x=代入 ≠0,
∴原方程的解为x=.
考点一 解分式方程
题型03 分式方程的特殊解法
类型三 列项相消法
方法简介:根据分式方程的结果特点,依据公式“化积为差,裂项相消,简化难度.
【例5】我们把分子是1的分数叫做分数单位,有些单位分数可以拆成两个不同的分数的差,如,;,,……,请用观察到的规律解方程,该方程解是多少?
解:
原方程化简为:,即,
方程两边同乘,得:,解得.
经检验是原方程的解,∴原方程的解为.
考点一 解分式方程
题型03 分式方程的特殊解法
类型三 列项相消法
【对点训练1】因为,
所以.解答下列问题:
(1)在和式中,第九项是______________;第项是______________.
(2)解方程:.
原方程可化简为:
方程两边同时乘,得:,
解得:,
经检验,是原方程的解.
【例6】用换元法解分式方程时,若设,则原方程可以化为整式方程 .
【对点训练1】用换元法解:.
02
考点一 解分式方程
题型03 分式方程的特殊解法
类型四 消元法
方法简介:当方程中的分式互为倒数,或不同分式中的分母互为相反式,或方程中分子、分母的二次项与一次项分别相同时,可考虑用换元法.
解:设,则原方程化为.
方程两边同时乘,得,解得.
经检验:都是的解.
当时,,解得.当时,,解得.
经检验:和都是原分式方程的解.
所以原分式方程的解为和.
【例7】(2022·贵州毕节·统考中考真题)小明解分式方程的过程下.
解:去分母,得 .①
去括号,得 .②
移项、合并同类项,得 .③
化系数为1,得 .④
以上步骤中,开始出错的一步是( )
A.① B.② C.③ D.④
02
考点一 解分式方程
题型04 错看或错解分式方程问题
先化简,再求值:,其中
解:原式
02
考点一 解分式方程
题型04 错看或错解分式方程问题
【对点训练1】(2022·浙江台州·统考中考真题)如图的解题过程中,第①步出现错误,但最后所求的值是正确的,则图中被污染的的值是 .
5
02
考点一 解分式方程
题型05 解分式方程的运用(新定义运算)
-0.5
【例8】(2022·河南平顶山·统考二模)定义运算,如:.则方程的解为( ) A. B. C. D.
【对点训练1】(2023 广西大学附属中学二模)对于实数a和b,定义一种新运算“ ”为:,这里等式右边是实数运算,例如:,则方程的解是( )
A. B. C. D.
【对点训练2】(2022·浙江宁波·统考中考真题)定义一种新运算:对于任意的非零实数a,b,.若,则x的值为 .
【例9】(2020·黑龙江齐齐哈尔·统考中考真题)若关于x的分式方程=+5的解为正数,则m的取值范围为( )
A.m<﹣10 B.m≤﹣10 C.m≥﹣10且m≠﹣6 D.m>﹣10且m≠﹣6
【对点训练9-1】(2020·四川泸州·中考真题)已知关于x的分式方程的解为非负数,则正整数m的所有个数为( )
A.3 B.4 C.5 D.6
02
考点一 解分式方程
题型06 根据分式方程解的情况求值
解:去分母得,解得,
由方程的解为正数,得到,且,,
则m的范围为且,故选:D.
解:去分母,得:m+2(x-1)=3,
移项、合并,解得:x=,
∵分式方程的解为非负数,∴≥0且≠1,解得:m≤5且m≠3,
∵m为正整数∴m=1,2,4,5,共4个,故选:B.
02
方法技巧
考点一 解分式方程
由分式方程的解的情况求字母系数的取值范围,一般解法是:
①根据未知数的范围求出字母的范围;
②把使分母为0的未知数的值代入到去分母后的整式方程中,求出对应的字母系数的值;
③综合①②,求出字母系数的范围.
【例10】(2022·四川遂宁·统考中考真题)若关于x的方程无解,则m的值为( )
A.0 B.4或6 C.6 D.0或4
【对点训练1】(2022·四川眉山·统考一模)已知关于的分式方程-=1无解,则=( )
A.-3 B.1 C.2 D.3
02
考点一 解分式方程
题型07 根据分式方程有解或无解求参数
方程两边同乘,得,整理得,
原方程无解,当时,;
当时,或,此时,,解得或,
当时,无解;当时,,解得;
综上,m的值为0或4;故选:D.
02
方法技巧
考点一 解分式方程
已知分式方程的解确定字母参数,首先将分式方程化为整式方程,用含字母参数的代数式表x,再根据解的情况确定字母参数的取值. 同时要注意原分式方程的最简公分母不能为零.
【例11】(2021·广西贺州·统考中考真题)若关于的分式方程有增根,则的值为( )
A.2 B.3 C.4 D.5
【对点训练1】(2021·山东烟台·统考一模)若关于x的分式方程有增根,则a的值为( )
A. 3 B.3 C.2 D.
02
考点一 解分式方程
题型08 已知分式方程有增根求参数
解:∵分式方程有增根,∴,
去分母,得,
将代入,得,
解得.
故选:D.
02
方法技巧
考点一 解分式方程
依据分式方程的增根确定字母参数的值的一般步骤:
1)先将分式方程转化为整式方程;
2)由题意求出增根;
3)将增根代入所化得的整式方程,解之就可得到字母参数的值.
【例12】(2022·广东佛山·统考一模)若关于x的分式方程=有正整数解,则整数m为 .
【对点训练1】(2020·重庆·统考中考真题)若关于x的一元一次不等式结 的解集为;且关于的分式方程有正整数解,则所有满足条件的整数a的值之积是( )
A.7 B.-14 C.28 D.-56
02
考点一 解分式方程
题型09 已知分式方程有整数解求参数
0
解:解不等式,解得x≤7,
∴不等式组整理的 ,由解集为x≤a,得到a≤7,
分式方程去分母得:y a+3y 4=y 2,即3y 2=a,解得:y=,
由y为正整数解且y≠2,得到a=1,7,所以1×7=7,故选:A.
考点二 分式方程的应用
用分式方程解决实际问题的步骤:
审:理解并找出实际问题中的等量关系;
设:用代数式表示实际问题中的基础数据;
列:找到所列代数式中的等量关系,以此为依据列出方程;
解:求解方程;
验:考虑求出的解是否具有实际意义;+
1)检验所求的解是否是所列分式方程的解.
2)检验所求的解是否符合实际意义.
答:实际问题的答案.
考点二 分式方程的应用
与分式方程有关应用题的常见类型:
【例1】(2022·云南·中考真题)某地开展建设绿色家园活动,活动期间,计划每天种植相同数量的树木,该活动开始后、实际每天比原计划每天多植树50棵,实际植树400棵所需时间与原计划植树300棵所需时间相同.设实际每天植树x棵.则下列方程正确的是( )
A. B. C. D.
【变式1-4】(2022·山东济宁·统考中考真题)一辆汽车开往距出发地420km的目的地,若这辆汽车比原计划每小时多行10km,则提前1小时到达目的地.设这辆汽车原计划的速度是x km/h,根据题意所列方程是( )
A. B.C. D.
【变式1-3】(2022·山东淄博·统考中考真题)为扎实推进“五育”并举工作,加强劳动教育,某校投入2万元购进了一批劳动工具.开展课后服务后,学生的劳动实践需求明显增强,需再次采购一批相同的劳动工具,已知采购数量与第一次相同,但采购单价比第一次降低10元,总费用降低了15%.设第二次采购单价为x元,则下列方程中正确的是( )
A. B. C.D.
02
考点二 分式方程的应用
题型01 列分式方程
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(行程问题)
【例2】(2022·四川自贡·统考中考真题)学校师生去距学校45千米的吴玉章故居开展研学活动,骑行爱好者张老师骑自行车先行2小时后,其余师生乘汽车出发,结果同时到达;已知汽车速度是自行车速度的3倍,求张老师骑车的速度.
解:设张老师骑车的速度为千米/小时,则汽车速度是千米/小时,
根据题意得:,
解之得,
经检验是分式方程的解,
答:张老师骑车的速度为千米/小时.
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(工程问题)
【例3】(2023重庆市模拟预测)为方便群众出行,甲、乙两个工程队负责修建某段通往高铁站的快线,已知甲队每天修路的长度是乙队的1.5倍,如果两队各自修建快线600m,甲队比乙队少用4天.
(1)求甲,乙两个工程队每天各修路多少米?
(2)现计划再修建长度为3000m的快线,由甲、乙两个工程队来完成.若甲队每天所需费用为1万元,乙队每天所需费用为0.6万元,求在总费用不超过38万元的情况下,至少安排乙工程队施工多少天?
(1)解:(1)设乙工程队每天修路x米,则甲工程队每天修路米,
依题意,得: ,
解得:x=50, 经检验,x=50是原方程的解,且符合题意,
∴.
答:甲工程队每天修路75米,乙工程队每天修路50米.
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(工程问题)
【例3】(2023重庆市模拟预测)为方便群众出行,甲、乙两个工程队负责修建某段通往高铁站的快线,已知甲队每天修路的长度是乙队的1.5倍,如果两队各自修建快线600m,甲队比乙队少用4天.
(1)求甲,乙两个工程队每天各修路多少米?
(2)现计划再修建长度为3000m的快线,由甲、乙两个工程队来完成.若甲队每天所需费用为1万元,乙队每天所需费用为0.6万元,求在总费用不超过38万元的情况下,至少安排乙工程队施工多少天?
(2)解:设安排乙工程队施工m天,则安排甲工程队施工天,
依题意,得:,
解得:m≥30.
答:至少安排乙工程队施工30天.
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(和差倍分问题)
【例4】(2022·广东深圳·深圳中学校考一模)2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,很快销售一空,第二次又用48000元购进同款冰墩墩,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进冰墩墩多少个?
(2)若所有冰墩墩都按相同的标价销售,要求全部销售完后的利润率不低于20%(不考虑其他因素),那么每个冰墩墩的标价至少为多少元?
(1)解:设第一次购进冰墩墩x个,则第二次购进2x个,
根据题意,得,
解得x=200,
经检验,x=200是原方程得解,且符合题意.
所以该商家第一次购进冰墩墩200个;
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(和差倍分问题)
【例4】(2022·广东深圳·深圳中学校考一模)2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,很快销售一空,第二次又用48000元购进同款冰墩墩,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进冰墩墩多少个?
(2)若所有冰墩墩都按相同的标价销售,要求全部销售完后的利润率不低于20%(不考虑其他因素),那么每个冰墩墩的标价至少为多少元?
解:由(1)可知第二次购进冰墩墩的数量是400个,设每个冰墩墩得标价是a元,得
(200+400)a≥(1+20%)(22000+48000),
解得a≥140.
所以每个冰墩墩得标价是140元.
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(销售利润问题)
【例5】(2023梁山县三模)某商场计划销售A,B两种型号的商品,经调查,用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多30元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该商场购进A,B型商品共100件进行试销,其中A型商品的件数不大于B型的件数,已知A型商品的售价为200元/件,B型商品的售价为180元/件,且全部能售出,求该商品能获得的利润最小是多少?
(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+30)元.
由题意: 解得x=120,
经检验x=120是分式方程的解,
答:一件B型商品的进价为120元,则一件A型商品的进价为150元.
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(销售利润问题)
【例5】(2023梁山县三模)某商场计划销售A,B两种型号的商品,经调查,用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多30元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该商场购进A,B型商品共100件进行试销,其中A型商品的件数不大于B型的件数,已知A型商品的售价为200元/件,B型商品的售价为180元/件,且全部能售出,求该商品能获得的利润最小是多少?
因为客商购进A型商品m件,销售利润为w元.
m≤100﹣m,∴m≤50,
由题意:w=m(200﹣150)+(100﹣m)(180﹣120)=﹣10m+6000,
∴m=50时,w有最小值=5500(元)
感谢观看
THANK YOU
第06讲 分式方程
2024年中考数学一轮复习讲练测
目录
CONTENTS
01
02
知识建构
03
考点精讲
考情分析
第一部分
考情分析
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
考点要求 新课标要求 命题预测
解分式方程 能解可化为一元一次方程的分式方程 中考中本考点考查内容以分式方程解法、分式方程含参问题、分式方程的应用题为主,既有单独考查,也有和一次函数、二次函数结合考察,年年考查,分值为10分左右.预计2024年各地中考还将继续考查分式方程解法、分式方程含参问题(较难)、分式方程的应用题,为避免丢分,学生应扎实掌握.
分式方程的应用 能根据具体问题的实际意义,检验方程解的合理性
第二部分
知识建构
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
第三部分
考点精讲
考点一 解分式方程
分式方程的概念:分母中含有未知数的方程叫做分式方程.
增根的概念:在方程变形时,有时可能产生不适合原方程的根,这种根叫做方程的增根.
考点一
考点一 解分式方程
02
考点一
易混易错
考点一 解分式方程
1. 分式方程与整式方程的根本区别:分母中含有未知数,也是判断分式方程的依据.
2. 去分母时要把方程两边的式子作为一个整体,记得不要漏乘整式项.
3. 分式方程的结果还要代回方程的最简公分母中,只有最简公分母不是零的解才是原方程的解.
4. 分式方程的增根是去分母后的整式方程的根,也是使分式方程的公分母为0的根,它不是原分式方程的根.
5. 解分式方程可能产生使分式方程无意义的根,检验是解分式方程的必要步骤.
6. 分式方程有增根与无解并非是同一个概念.分式方程无解,需分类讨论:可能是解为增根,也可能是去分母后的整式方程无解.
【例1】(2021·河南信阳·河南省淮滨县第一中学校考模拟预测)下列方程:①;②;③;④(为已知数),其中分式方程有( )
A.个 B.个 C.个 D.个
【对点训练1】(2022 南明区 二模)下列关于的方程,是分式方程的是( )
A. B. C. D.
02
考点一 解分式方程
题型01 判断分式方程
【例2】(2023·辽宁大连·统考中考真题)将方程去分母,两边同乘后的式子为( )
A. B.
C. D.
【对点训练1】(2023·内蒙古赤峰·统考中考真题)方程的解为 .
【对点训练2】(2022·山东济南·统考中考真题)代数式与代数式的值相等,则x= .
【对点训练3】(2022·湖南常德·统考中考真题)方程的解为 .
02
考点一 解分式方程
题型02 分式方程的一般解法
x=4
7
x=4
02
方法技巧
考点一 解分式方程
解分式方程方法:
先通过方程两边同乘最简公分母将分式方程化为整式方程,再解整式方程,最后需要检验整式方程的解是不是分式方程的解.
02
考点一 解分式方程
题型03 分式方程的特殊解法
类型一 分组通分法
方法简介:如果整个方程一起通分,计算量大又易出错,观察方程中分母的特点可联想分组通分求解.
【例3】解方程:
【详解】解:原方程可变形为,
当5-x≠0时,解得x1=
当5-x=0时,解得x2=
经检验,x1=x2=都是原方程得解.
02
考点一 解分式方程
题型03 分式方程的特殊解法
类型二 分离分式法
方法简介:每个分式的分母与分子相差1,利用这个特点可采用分类分式法求解.
【例4】解方程:
解:原方程可变形为,,
化简得,,即,
∴2x+5=0,解得,x=,
检验,把x=代入 ≠0,
∴原方程的解为x=.
考点一 解分式方程
题型03 分式方程的特殊解法
类型三 列项相消法
方法简介:根据分式方程的结果特点,依据公式“化积为差,裂项相消,简化难度.
【例5】我们把分子是1的分数叫做分数单位,有些单位分数可以拆成两个不同的分数的差,如,;,,……,请用观察到的规律解方程,该方程解是多少?
解:
原方程化简为:,即,
方程两边同乘,得:,解得.
经检验是原方程的解,∴原方程的解为.
考点一 解分式方程
题型03 分式方程的特殊解法
类型三 列项相消法
【对点训练1】因为,
所以.解答下列问题:
(1)在和式中,第九项是______________;第项是______________.
(2)解方程:.
原方程可化简为:
方程两边同时乘,得:,
解得:,
经检验,是原方程的解.
【例6】用换元法解分式方程时,若设,则原方程可以化为整式方程 .
【对点训练1】用换元法解:.
02
考点一 解分式方程
题型03 分式方程的特殊解法
类型四 消元法
方法简介:当方程中的分式互为倒数,或不同分式中的分母互为相反式,或方程中分子、分母的二次项与一次项分别相同时,可考虑用换元法.
解:设,则原方程化为.
方程两边同时乘,得,解得.
经检验:都是的解.
当时,,解得.当时,,解得.
经检验:和都是原分式方程的解.
所以原分式方程的解为和.
【例7】(2022·贵州毕节·统考中考真题)小明解分式方程的过程下.
解:去分母,得 .①
去括号,得 .②
移项、合并同类项,得 .③
化系数为1,得 .④
以上步骤中,开始出错的一步是( )
A.① B.② C.③ D.④
02
考点一 解分式方程
题型04 错看或错解分式方程问题
先化简,再求值:,其中
解:原式
02
考点一 解分式方程
题型04 错看或错解分式方程问题
【对点训练1】(2022·浙江台州·统考中考真题)如图的解题过程中,第①步出现错误,但最后所求的值是正确的,则图中被污染的的值是 .
5
02
考点一 解分式方程
题型05 解分式方程的运用(新定义运算)
-0.5
【例8】(2022·河南平顶山·统考二模)定义运算,如:.则方程的解为( ) A. B. C. D.
【对点训练1】(2023 广西大学附属中学二模)对于实数a和b,定义一种新运算“ ”为:,这里等式右边是实数运算,例如:,则方程的解是( )
A. B. C. D.
【对点训练2】(2022·浙江宁波·统考中考真题)定义一种新运算:对于任意的非零实数a,b,.若,则x的值为 .
【例9】(2020·黑龙江齐齐哈尔·统考中考真题)若关于x的分式方程=+5的解为正数,则m的取值范围为( )
A.m<﹣10 B.m≤﹣10 C.m≥﹣10且m≠﹣6 D.m>﹣10且m≠﹣6
【对点训练9-1】(2020·四川泸州·中考真题)已知关于x的分式方程的解为非负数,则正整数m的所有个数为( )
A.3 B.4 C.5 D.6
02
考点一 解分式方程
题型06 根据分式方程解的情况求值
解:去分母得,解得,
由方程的解为正数,得到,且,,
则m的范围为且,故选:D.
解:去分母,得:m+2(x-1)=3,
移项、合并,解得:x=,
∵分式方程的解为非负数,∴≥0且≠1,解得:m≤5且m≠3,
∵m为正整数∴m=1,2,4,5,共4个,故选:B.
02
方法技巧
考点一 解分式方程
由分式方程的解的情况求字母系数的取值范围,一般解法是:
①根据未知数的范围求出字母的范围;
②把使分母为0的未知数的值代入到去分母后的整式方程中,求出对应的字母系数的值;
③综合①②,求出字母系数的范围.
【例10】(2022·四川遂宁·统考中考真题)若关于x的方程无解,则m的值为( )
A.0 B.4或6 C.6 D.0或4
【对点训练1】(2022·四川眉山·统考一模)已知关于的分式方程-=1无解,则=( )
A.-3 B.1 C.2 D.3
02
考点一 解分式方程
题型07 根据分式方程有解或无解求参数
方程两边同乘,得,整理得,
原方程无解,当时,;
当时,或,此时,,解得或,
当时,无解;当时,,解得;
综上,m的值为0或4;故选:D.
02
方法技巧
考点一 解分式方程
已知分式方程的解确定字母参数,首先将分式方程化为整式方程,用含字母参数的代数式表x,再根据解的情况确定字母参数的取值. 同时要注意原分式方程的最简公分母不能为零.
【例11】(2021·广西贺州·统考中考真题)若关于的分式方程有增根,则的值为( )
A.2 B.3 C.4 D.5
【对点训练1】(2021·山东烟台·统考一模)若关于x的分式方程有增根,则a的值为( )
A. 3 B.3 C.2 D.
02
考点一 解分式方程
题型08 已知分式方程有增根求参数
解:∵分式方程有增根,∴,
去分母,得,
将代入,得,
解得.
故选:D.
02
方法技巧
考点一 解分式方程
依据分式方程的增根确定字母参数的值的一般步骤:
1)先将分式方程转化为整式方程;
2)由题意求出增根;
3)将增根代入所化得的整式方程,解之就可得到字母参数的值.
【例12】(2022·广东佛山·统考一模)若关于x的分式方程=有正整数解,则整数m为 .
【对点训练1】(2020·重庆·统考中考真题)若关于x的一元一次不等式结 的解集为;且关于的分式方程有正整数解,则所有满足条件的整数a的值之积是( )
A.7 B.-14 C.28 D.-56
02
考点一 解分式方程
题型09 已知分式方程有整数解求参数
0
解:解不等式,解得x≤7,
∴不等式组整理的 ,由解集为x≤a,得到a≤7,
分式方程去分母得:y a+3y 4=y 2,即3y 2=a,解得:y=,
由y为正整数解且y≠2,得到a=1,7,所以1×7=7,故选:A.
考点二 分式方程的应用
用分式方程解决实际问题的步骤:
审:理解并找出实际问题中的等量关系;
设:用代数式表示实际问题中的基础数据;
列:找到所列代数式中的等量关系,以此为依据列出方程;
解:求解方程;
验:考虑求出的解是否具有实际意义;+
1)检验所求的解是否是所列分式方程的解.
2)检验所求的解是否符合实际意义.
答:实际问题的答案.
考点二 分式方程的应用
与分式方程有关应用题的常见类型:
【例1】(2022·云南·中考真题)某地开展建设绿色家园活动,活动期间,计划每天种植相同数量的树木,该活动开始后、实际每天比原计划每天多植树50棵,实际植树400棵所需时间与原计划植树300棵所需时间相同.设实际每天植树x棵.则下列方程正确的是( )
A. B. C. D.
【变式1-4】(2022·山东济宁·统考中考真题)一辆汽车开往距出发地420km的目的地,若这辆汽车比原计划每小时多行10km,则提前1小时到达目的地.设这辆汽车原计划的速度是x km/h,根据题意所列方程是( )
A. B.C. D.
【变式1-3】(2022·山东淄博·统考中考真题)为扎实推进“五育”并举工作,加强劳动教育,某校投入2万元购进了一批劳动工具.开展课后服务后,学生的劳动实践需求明显增强,需再次采购一批相同的劳动工具,已知采购数量与第一次相同,但采购单价比第一次降低10元,总费用降低了15%.设第二次采购单价为x元,则下列方程中正确的是( )
A. B. C.D.
02
考点二 分式方程的应用
题型01 列分式方程
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(行程问题)
【例2】(2022·四川自贡·统考中考真题)学校师生去距学校45千米的吴玉章故居开展研学活动,骑行爱好者张老师骑自行车先行2小时后,其余师生乘汽车出发,结果同时到达;已知汽车速度是自行车速度的3倍,求张老师骑车的速度.
解:设张老师骑车的速度为千米/小时,则汽车速度是千米/小时,
根据题意得:,
解之得,
经检验是分式方程的解,
答:张老师骑车的速度为千米/小时.
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(工程问题)
【例3】(2023重庆市模拟预测)为方便群众出行,甲、乙两个工程队负责修建某段通往高铁站的快线,已知甲队每天修路的长度是乙队的1.5倍,如果两队各自修建快线600m,甲队比乙队少用4天.
(1)求甲,乙两个工程队每天各修路多少米?
(2)现计划再修建长度为3000m的快线,由甲、乙两个工程队来完成.若甲队每天所需费用为1万元,乙队每天所需费用为0.6万元,求在总费用不超过38万元的情况下,至少安排乙工程队施工多少天?
(1)解:(1)设乙工程队每天修路x米,则甲工程队每天修路米,
依题意,得: ,
解得:x=50, 经检验,x=50是原方程的解,且符合题意,
∴.
答:甲工程队每天修路75米,乙工程队每天修路50米.
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(工程问题)
【例3】(2023重庆市模拟预测)为方便群众出行,甲、乙两个工程队负责修建某段通往高铁站的快线,已知甲队每天修路的长度是乙队的1.5倍,如果两队各自修建快线600m,甲队比乙队少用4天.
(1)求甲,乙两个工程队每天各修路多少米?
(2)现计划再修建长度为3000m的快线,由甲、乙两个工程队来完成.若甲队每天所需费用为1万元,乙队每天所需费用为0.6万元,求在总费用不超过38万元的情况下,至少安排乙工程队施工多少天?
(2)解:设安排乙工程队施工m天,则安排甲工程队施工天,
依题意,得:,
解得:m≥30.
答:至少安排乙工程队施工30天.
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(和差倍分问题)
【例4】(2022·广东深圳·深圳中学校考一模)2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,很快销售一空,第二次又用48000元购进同款冰墩墩,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进冰墩墩多少个?
(2)若所有冰墩墩都按相同的标价销售,要求全部销售完后的利润率不低于20%(不考虑其他因素),那么每个冰墩墩的标价至少为多少元?
(1)解:设第一次购进冰墩墩x个,则第二次购进2x个,
根据题意,得,
解得x=200,
经检验,x=200是原方程得解,且符合题意.
所以该商家第一次购进冰墩墩200个;
02
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(和差倍分问题)
【例4】(2022·广东深圳·深圳中学校考一模)2022年北京冬奥会吉祥物冰墩墩深受大家的喜欢.某商家两次购进冰墩墩进行销售,第一次用22000元,很快销售一空,第二次又用48000元购进同款冰墩墩,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进冰墩墩多少个?
(2)若所有冰墩墩都按相同的标价销售,要求全部销售完后的利润率不低于20%(不考虑其他因素),那么每个冰墩墩的标价至少为多少元?
解:由(1)可知第二次购进冰墩墩的数量是400个,设每个冰墩墩得标价是a元,得
(200+400)a≥(1+20%)(22000+48000),
解得a≥140.
所以每个冰墩墩得标价是140元.
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(销售利润问题)
【例5】(2023梁山县三模)某商场计划销售A,B两种型号的商品,经调查,用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多30元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该商场购进A,B型商品共100件进行试销,其中A型商品的件数不大于B型的件数,已知A型商品的售价为200元/件,B型商品的售价为180元/件,且全部能售出,求该商品能获得的利润最小是多少?
(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+30)元.
由题意: 解得x=120,
经检验x=120是分式方程的解,
答:一件B型商品的进价为120元,则一件A型商品的进价为150元.
考点二 分式方程的应用
题型02 利用分式方程解决实际问题(销售利润问题)
【例5】(2023梁山县三模)某商场计划销售A,B两种型号的商品,经调查,用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多30元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该商场购进A,B型商品共100件进行试销,其中A型商品的件数不大于B型的件数,已知A型商品的售价为200元/件,B型商品的售价为180元/件,且全部能售出,求该商品能获得的利润最小是多少?
因为客商购进A型商品m件,销售利润为w元.
m≤100﹣m,∴m≤50,
由题意:w=m(200﹣150)+(100﹣m)(180﹣120)=﹣10m+6000,
∴m=50时,w有最小值=5500(元)
感谢观看
THANK YOU
同课章节目录
