数学人教A版(2019)选择性必修第一册3.3.2抛物线的简单几何性质 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.3.2抛物线的简单几何性质 课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
3.3.2抛物线的简单几何性质
新知探究
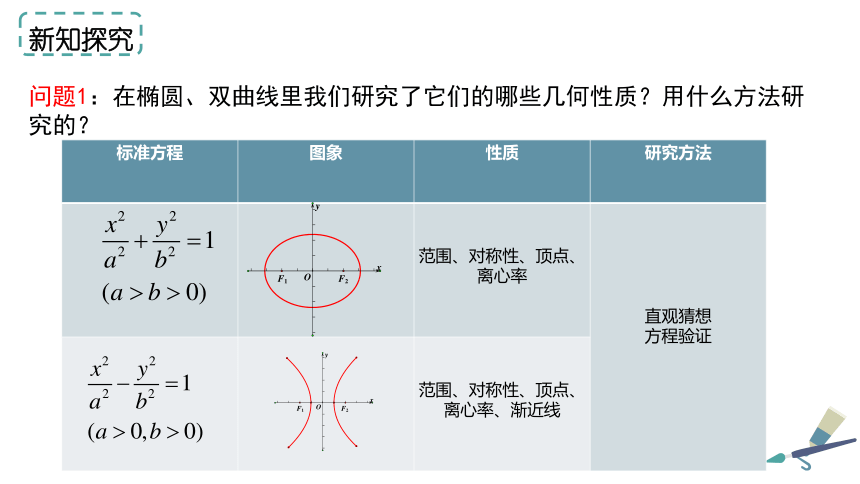
问题1:在椭圆、双曲线里我们研究了它们的哪些几何性质?用什么方法研究的?
标准方程 图象 性质 研究方法
范围、对称性、顶点、离心率
直观猜想
方程验证
范围、对称性、顶点、离心率、渐近线
新知探究
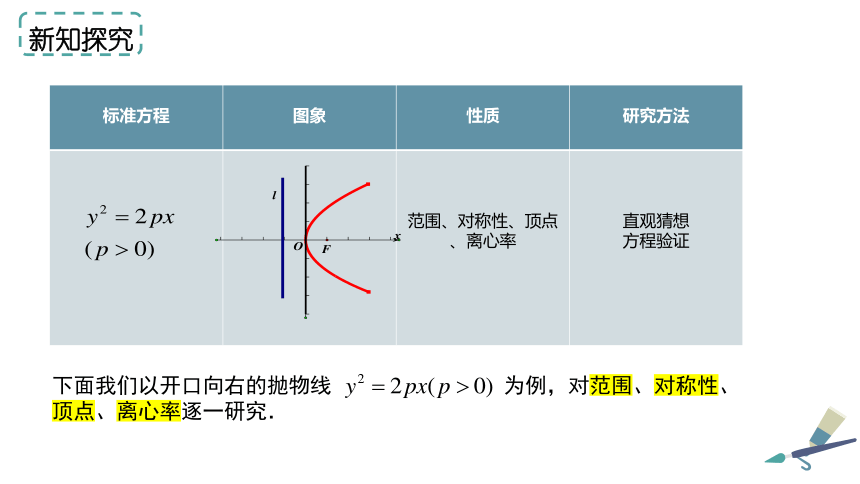
标准方程 图象 性质
研究方法
范围、对称性、顶点、离心率
直观猜想
方程验证
下面我们以开口向右的抛物线 为例,对范围、对称性、顶点、离心率逐一研究.
新知探究
范围
因为,由方程①可知,对于抛物线上的点,,,当时,抛物线在轴的右侧,开口方向与轴的正方向相同;当的值增大时,的值也增大,这说明抛物线向右上方和右下方无限延伸.
抛物线 ①
新知探究
对称性
抛物线 ①
以代,方程①不变,所以抛物线关于轴对称.我们把抛物线的对称轴叫做抛物线的轴.
新知探究
顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程①中,当时,,因此抛物线的顶点就是原点.
抛物线 ①
新知探究
离心率
抛物线上的点与焦点的距离和点到准线的距离的比,叫做抛物线的离心率,用表示.由抛物线的定义可知,.
抛物线 ①
习题训练
例1:已知抛物线关于 轴对称,它的顶点在原点,且经过点 ,求它的标准方程.
习题训练
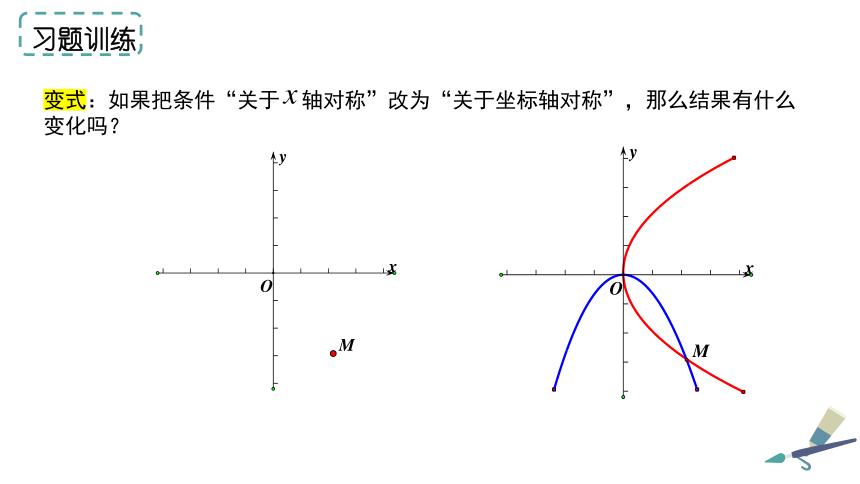
变式:如果把条件“关于 轴对称”改为“关于坐标轴对称”,那么结果有什么变化吗?
习题训练
难点1:求抛物线方程的问题
抛物线过某定点,求抛物线方程时,要注意两点:
1、关注问题是否说明抛物线的对称轴;
2、要准确设出抛物线方程,做到不重不漏.
习题训练
在图中,设,.由抛物线的定义可知,等于点到准线的距离.由,,得,于是.同理,,于是得.由此可见,只要求出点得横坐标之和,就可以求出.
例2.斜率为1的直线经过抛物线的焦点,且与抛物线相交于两点,求线段的长.
习题训练
思考:如果直线不经过焦点 ,那么 还等于 吗?
图象角度:
.
根据三角形两边之和大于第三边,
习题训练
变式
难点2:弦长问题
面对直线与抛物线相交问题,利用坐标法求解线段长时,可以先判断直线是否过抛物线的焦点。
若直线不过抛物线焦点,则利用两点间距离公式进行求解;
若直线过抛物线的焦点,可结合抛物线的图象,使用抛物线的定义进行快速求解.
习题训练
变式 .过抛物线的焦点作倾斜角为直线交抛物线于,两点, 如果,求线段的长.
解:因为抛物线的焦点是,
所以直线的方程为,
与抛物线方程联立消去得,
所以,从而.
习题训练
例3.已知是抛物线上两点,为坐标原点,若,且的垂心恰是此抛物线的焦点,求直线的方程.
解:由题知,抛物线的焦点.
∵抛物线关于轴对称,,∴为等腰三角形.
∴两点关于轴对称.
设,则.∵的垂心恰为抛物线的焦点,
∴,则,即.
又∵,∴.
∴直线的方程为.
习题训练
变式. 正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线上,求这个正三角形的边长.
解:如图所示,设正三角形的顶点在抛物线上,且坐标分别为,,则,.
又,所以,即,
整理得.
∵,,,∴,由此可得,
即线段关于轴对称.由此得,
∴,与联立,解得.
∴.
易错点:抛物线的标准方程的形式
在判断抛物线的开口,求解抛物线的范围、焦点坐标等问题时,要注意观察抛物线是否为标准方程.
若给定的方程形如 ,则要先变形为标准方程 ,再对范围、对称轴进行判断、求解.
知识归纳
本节课我们研究了抛物线的哪些几何性质?
标准方程 图像 性质 范围 对称轴 顶点 离心率
3.3.2抛物线的简单几何性质
新知探究
问题1:在椭圆、双曲线里我们研究了它们的哪些几何性质?用什么方法研究的?
标准方程 图象 性质 研究方法
范围、对称性、顶点、离心率
直观猜想
方程验证
范围、对称性、顶点、离心率、渐近线
新知探究
标准方程 图象 性质
研究方法
范围、对称性、顶点、离心率
直观猜想
方程验证
下面我们以开口向右的抛物线 为例,对范围、对称性、顶点、离心率逐一研究.
新知探究
范围
因为,由方程①可知,对于抛物线上的点,,,当时,抛物线在轴的右侧,开口方向与轴的正方向相同;当的值增大时,的值也增大,这说明抛物线向右上方和右下方无限延伸.
抛物线 ①
新知探究
对称性
抛物线 ①
以代,方程①不变,所以抛物线关于轴对称.我们把抛物线的对称轴叫做抛物线的轴.
新知探究
顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程①中,当时,,因此抛物线的顶点就是原点.
抛物线 ①
新知探究
离心率
抛物线上的点与焦点的距离和点到准线的距离的比,叫做抛物线的离心率,用表示.由抛物线的定义可知,.
抛物线 ①
习题训练
例1:已知抛物线关于 轴对称,它的顶点在原点,且经过点 ,求它的标准方程.
习题训练
变式:如果把条件“关于 轴对称”改为“关于坐标轴对称”,那么结果有什么变化吗?
习题训练
难点1:求抛物线方程的问题
抛物线过某定点,求抛物线方程时,要注意两点:
1、关注问题是否说明抛物线的对称轴;
2、要准确设出抛物线方程,做到不重不漏.
习题训练
在图中,设,.由抛物线的定义可知,等于点到准线的距离.由,,得,于是.同理,,于是得.由此可见,只要求出点得横坐标之和,就可以求出.
例2.斜率为1的直线经过抛物线的焦点,且与抛物线相交于两点,求线段的长.
习题训练
思考:如果直线不经过焦点 ,那么 还等于 吗?
图象角度:
.
根据三角形两边之和大于第三边,
习题训练
变式
难点2:弦长问题
面对直线与抛物线相交问题,利用坐标法求解线段长时,可以先判断直线是否过抛物线的焦点。
若直线不过抛物线焦点,则利用两点间距离公式进行求解;
若直线过抛物线的焦点,可结合抛物线的图象,使用抛物线的定义进行快速求解.
习题训练
变式 .过抛物线的焦点作倾斜角为直线交抛物线于,两点, 如果,求线段的长.
解:因为抛物线的焦点是,
所以直线的方程为,
与抛物线方程联立消去得,
所以,从而.
习题训练
例3.已知是抛物线上两点,为坐标原点,若,且的垂心恰是此抛物线的焦点,求直线的方程.
解:由题知,抛物线的焦点.
∵抛物线关于轴对称,,∴为等腰三角形.
∴两点关于轴对称.
设,则.∵的垂心恰为抛物线的焦点,
∴,则,即.
又∵,∴.
∴直线的方程为.
习题训练
变式. 正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线上,求这个正三角形的边长.
解:如图所示,设正三角形的顶点在抛物线上,且坐标分别为,,则,.
又,所以,即,
整理得.
∵,,,∴,由此可得,
即线段关于轴对称.由此得,
∴,与联立,解得.
∴.
易错点:抛物线的标准方程的形式
在判断抛物线的开口,求解抛物线的范围、焦点坐标等问题时,要注意观察抛物线是否为标准方程.
若给定的方程形如 ,则要先变形为标准方程 ,再对范围、对称轴进行判断、求解.
知识归纳
本节课我们研究了抛物线的哪些几何性质?
标准方程 图像 性质 范围 对称轴 顶点 离心率
