2023—2024学年人教版数学八年级上册第十二章全等三角形单元检测试卷(无答案)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册第十二章全等三角形单元检测试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 294.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:47:48 | ||
图片预览

文档简介
数学第十二章全等三角形单元检测试卷
一、选择题
1.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A.40° B.30° C.35° D.25°
第1题 第3题 第4题 第5题 第6题
2.△ABC≌△DEF,AB=2,BC=4,若△DEF的周长为偶数,则DF的取值为( )
A.3 B.4 C.5 D.3或4或5
3.如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
A.∠ADB=∠ADC B.∠B=∠C C.DB=DC D.AB=AC
4.如图所示,AD是△ABC的高,延长BC至E,使CE=BC,△ABC的面积为S1,△ACE的面积为S2,那么( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
5.如图, 中,, 平分,,,则 的面积是 ( )
A. B. C. D.
6.如图, 平分 , 于点 , 于点 ,连接 交 于点 ,则下列结论:① ;② ;③ ;④ ,其中正确结论的个数是
A. 个 B. 个 C. 个 D. 个
7.为测量一池塘两端A,B间的距离.甲、乙两位同学分别设计了两种不同的方案.
甲:如图1,先过点B作AB的垂线BF,再在射线BF上取C,D两点,使BC=CD,接着过点作BD的垂线DE,交AC的延长线于点E.则测出DE的长即为A,B间的距离;
乙:如图2,先确定直线AB,过点B作射线BE,在射线BE上找可直接到达点A的点D,连接DA,作DC=DA,交直线AB于点C,则测出BC的长即为AB间的距离,则下列判断正确的是( )
只有甲同学的方案可行
B.只有乙同学的方案可行
甲、乙同学的方案均可行
D.甲、乙同学的方案均不可行
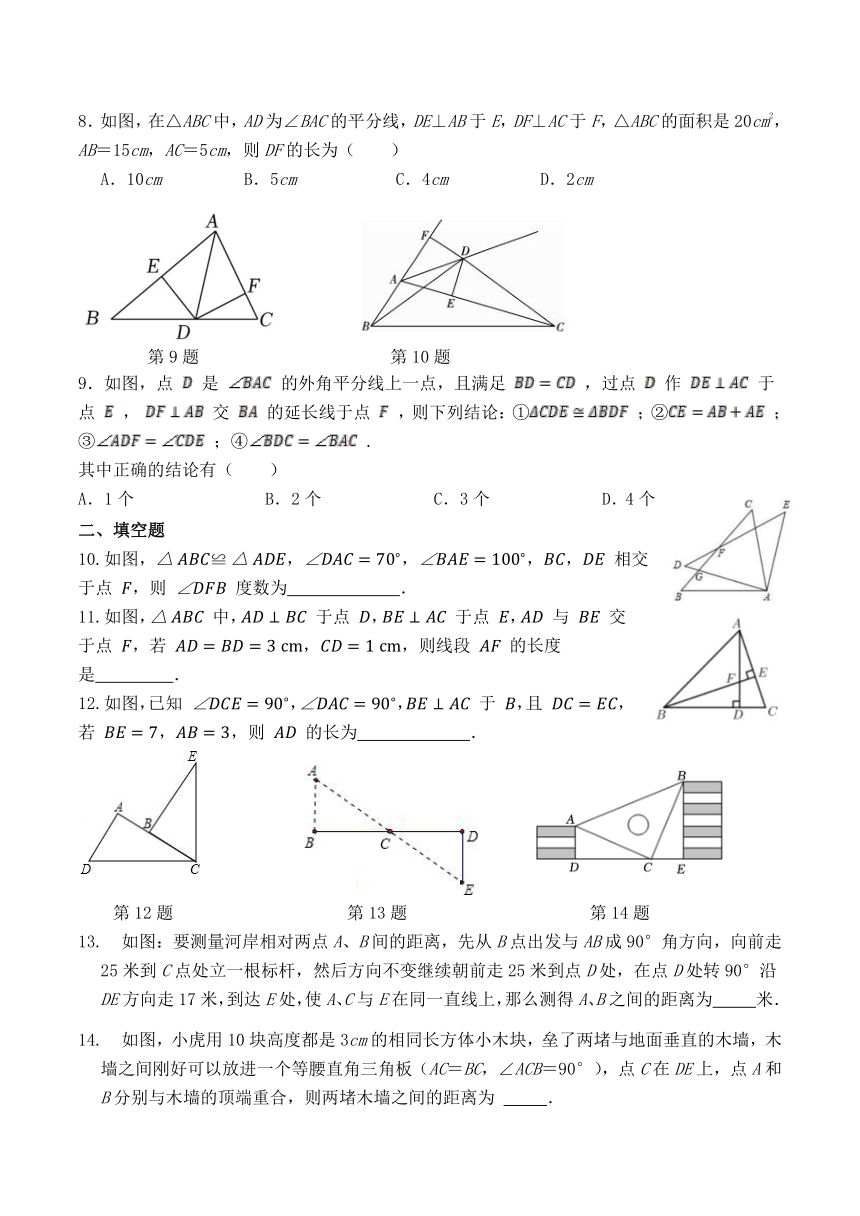
8.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是20cm2,AB=15cm,AC=5cm,则DF的长为( )
A.10cm B.5cm C.4cm D.2cm
第9题 第10题
9.如图,点 是 的外角平分线上一点,且满足 ,过点 作 于点 , 交 的延长线于点 ,则下列结论:① ;② ;③ ;④ .
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
10.如图,,,,, 相交于点 ,则 度数为 .
11.如图, 中, 于点 , 于点 , 与 交于点 ,若 ,,则线段 的长度是 .
12.如图,已知 ,, 于 ,且 ,若 ,,则 的长为 .
第12题 第13题 第14题
13. 如图:要测量河岸相对两点A、B间的距离,先从B点出发与AB成90°角方向,向前走25米到C点处立一根标杆,然后方向不变继续朝前走25米到点D处,在点D处转90°沿DE方向走17米,到达E处,使A、C与E在同一直线上,那么测得A、B之间的距离为 米.
14. 如图,小虎用10块高度都是3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 .
三、简答题
15.如图,AB∥EF,AC∥DE,FC=DB,求证:AB=EF.
16.如图,于点,于点,,交于点M.
(1)求证:;
(2)求证:.
如图,和中,,,且.
(1)求证:;
(2)若,求的度数.
18.【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,中,若,,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到,依据是___________.
A. B. C. D.
(2)由“三角形的三边关系”可求得的取值范围是___________.
【运用】
(3)如图2,是的中线,交于E,交于F,.若,,求线段BF的长.
19.小明的学习过程中,对教材中的一个有趣问题做如下探究:
(1)【习题回顾】已知:如图1,在中,,是角平分线,是高,相交于点.求证:;
(2)【变式思考】如图2,在中,,是边上的高,若的外角的平分线交的延长线于点,其反向延长线与边的延长线交于点,若,求和的度数;
(3)【探究延伸】如图3,在中,在上存在一点,使得,角平分线交于点.的外角的平分线所在直线与的延长线交于点.若,求的度数.
一、选择题
1.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A.40° B.30° C.35° D.25°
第1题 第3题 第4题 第5题 第6题
2.△ABC≌△DEF,AB=2,BC=4,若△DEF的周长为偶数,则DF的取值为( )
A.3 B.4 C.5 D.3或4或5
3.如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
A.∠ADB=∠ADC B.∠B=∠C C.DB=DC D.AB=AC
4.如图所示,AD是△ABC的高,延长BC至E,使CE=BC,△ABC的面积为S1,△ACE的面积为S2,那么( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
5.如图, 中,, 平分,,,则 的面积是 ( )
A. B. C. D.
6.如图, 平分 , 于点 , 于点 ,连接 交 于点 ,则下列结论:① ;② ;③ ;④ ,其中正确结论的个数是
A. 个 B. 个 C. 个 D. 个
7.为测量一池塘两端A,B间的距离.甲、乙两位同学分别设计了两种不同的方案.
甲:如图1,先过点B作AB的垂线BF,再在射线BF上取C,D两点,使BC=CD,接着过点作BD的垂线DE,交AC的延长线于点E.则测出DE的长即为A,B间的距离;
乙:如图2,先确定直线AB,过点B作射线BE,在射线BE上找可直接到达点A的点D,连接DA,作DC=DA,交直线AB于点C,则测出BC的长即为AB间的距离,则下列判断正确的是( )
只有甲同学的方案可行
B.只有乙同学的方案可行
甲、乙同学的方案均可行
D.甲、乙同学的方案均不可行
8.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是20cm2,AB=15cm,AC=5cm,则DF的长为( )
A.10cm B.5cm C.4cm D.2cm
第9题 第10题
9.如图,点 是 的外角平分线上一点,且满足 ,过点 作 于点 , 交 的延长线于点 ,则下列结论:① ;② ;③ ;④ .
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
10.如图,,,,, 相交于点 ,则 度数为 .
11.如图, 中, 于点 , 于点 , 与 交于点 ,若 ,,则线段 的长度是 .
12.如图,已知 ,, 于 ,且 ,若 ,,则 的长为 .
第12题 第13题 第14题
13. 如图:要测量河岸相对两点A、B间的距离,先从B点出发与AB成90°角方向,向前走25米到C点处立一根标杆,然后方向不变继续朝前走25米到点D处,在点D处转90°沿DE方向走17米,到达E处,使A、C与E在同一直线上,那么测得A、B之间的距离为 米.
14. 如图,小虎用10块高度都是3cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为 .
三、简答题
15.如图,AB∥EF,AC∥DE,FC=DB,求证:AB=EF.
16.如图,于点,于点,,交于点M.
(1)求证:;
(2)求证:.
如图,和中,,,且.
(1)求证:;
(2)若,求的度数.
18.【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,中,若,,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到,依据是___________.
A. B. C. D.
(2)由“三角形的三边关系”可求得的取值范围是___________.
【运用】
(3)如图2,是的中线,交于E,交于F,.若,,求线段BF的长.
19.小明的学习过程中,对教材中的一个有趣问题做如下探究:
(1)【习题回顾】已知:如图1,在中,,是角平分线,是高,相交于点.求证:;
(2)【变式思考】如图2,在中,,是边上的高,若的外角的平分线交的延长线于点,其反向延长线与边的延长线交于点,若,求和的度数;
(3)【探究延伸】如图3,在中,在上存在一点,使得,角平分线交于点.的外角的平分线所在直线与的延长线交于点.若,求的度数.
