【同步精讲-习题课件】第27章《相似》27.2.1 第3课时 相似三角形判定定理2-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第27章《相似》27.2.1 第3课时 相似三角形判定定理2-人教版数学九下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
27.2.1 相似三角形的判定
第3课时 相似三角形判定定理2
第二十七章 相似
必
●
知识要点全练
夯实基础
知识点1
两边成比例且夹角相等的两个三
角形相似
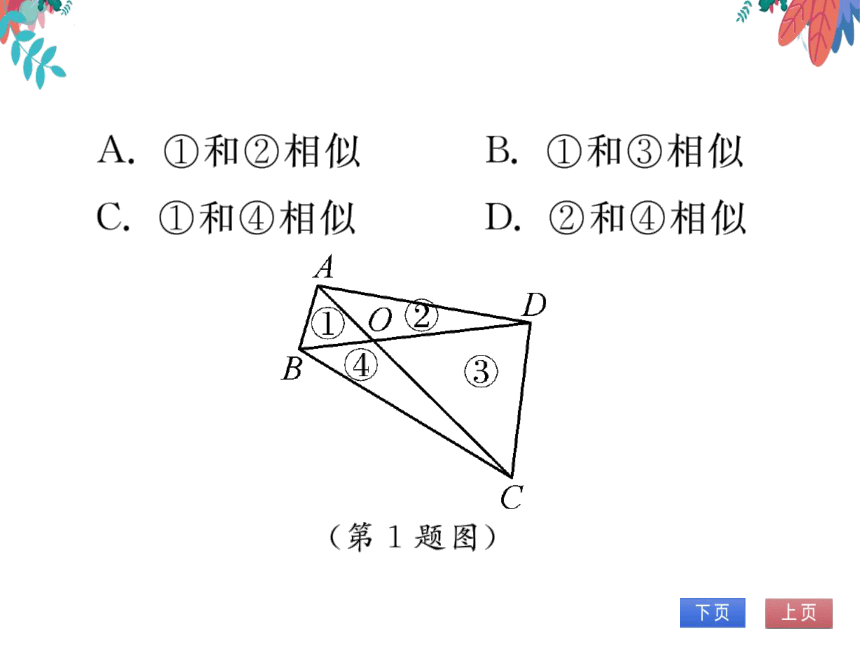
1.
(2022秋·四平期末)如图,四边形ABCD的
对角线AC、BD相交于O,且将这个四边形分
成①、②、③、④四个三角形,若OA:OC=OB:
OD,则下列结论中一定正确的是
B
A
y
B
3
C
(第1题图)
2.(2023春·信阳校考)如图,在△ABC中,
点D在边AC上,根据下列条件,能说明
△BDC∽△ABC的是
(C)
A.AB·CB=CA·CD
B.AB·CD=BD·BC
C.BC2=AC·DC
D.BD2=CD·DA
C
D
B
A
(第2题图)
3.(2023·江西新余)已知:如图,梯形ABCD
中,AB∥DC,∠B=90°,AB=3,BC=11,
DC=6.在线段BC上若存在点P,使得
△ABP与△PCD相似,则满足条件的P
点的个数为
B
A.4
B.3
C.2
D.1
D
A
B
C
(第3题图)
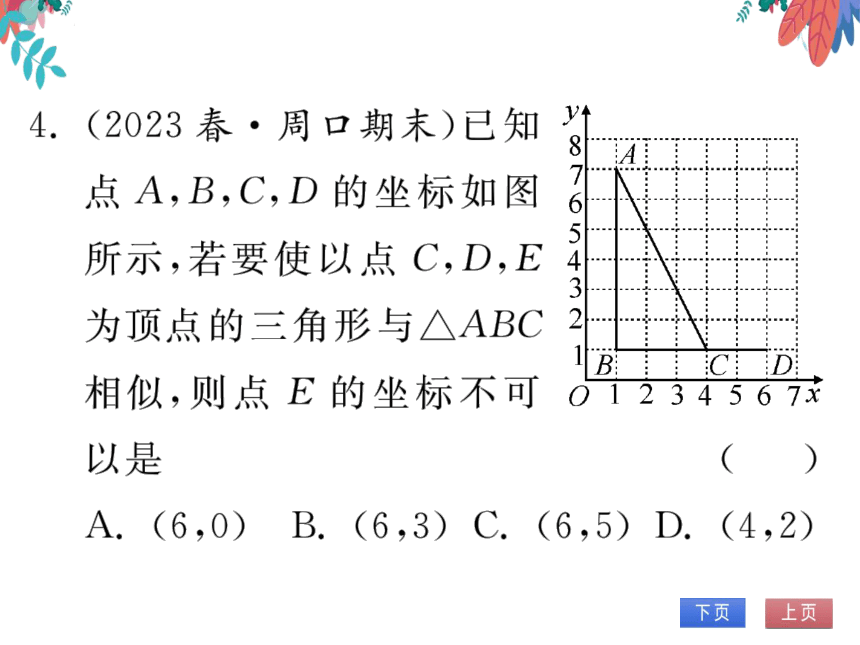
4.(2023春·周口期末)已知
↑
8
点A,B,C,D的坐标如图
所示,若要使以点C,D,E
4
3
为顶点的三角形与△ABC
B
C
D
相似,则点E的坐标不可
01234567x
以是
(B)
A.(6,0)
B.(6
,3)C.(6,5)D.(4,2)
A
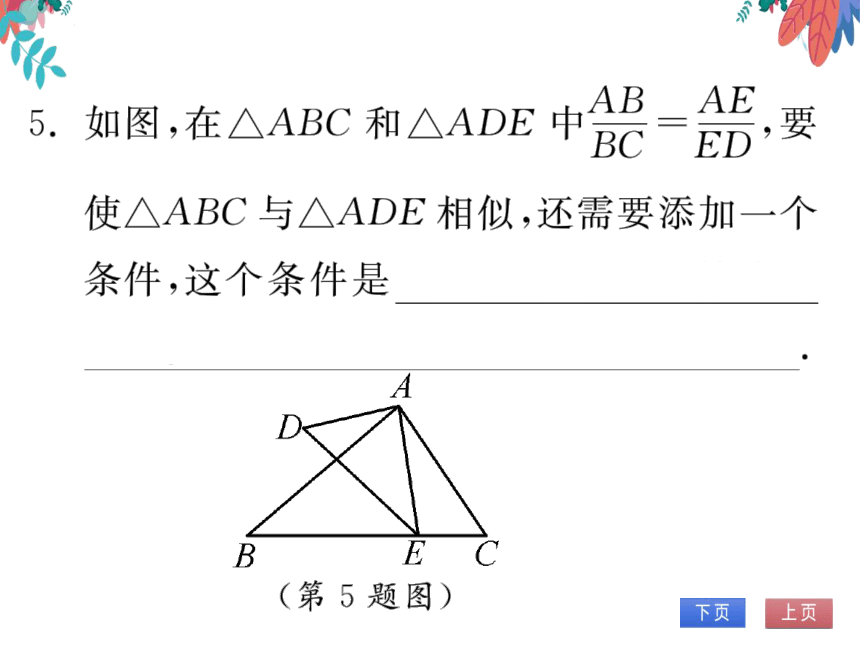
5.如图,在△ABC和△ADE
AE
B元-ED
要
使△ABC与△ADE相似,还需要添加一个
条件,这个条件是
∠B=∠AED(答案不
唯一)
A
B
E
C
(第5题图)
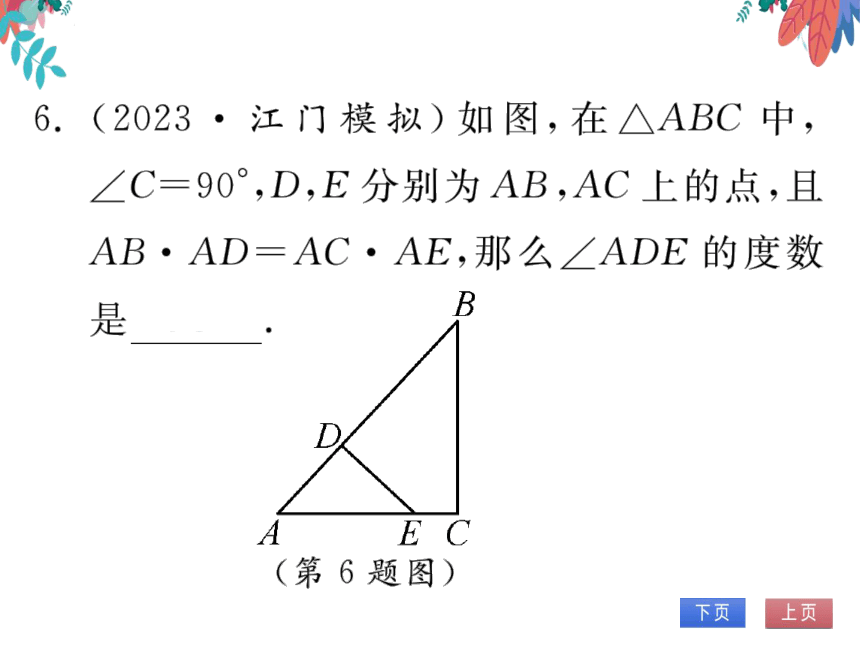
6.(2023·江门模拟)如图,在∧ABC中,
∠C=90°,D,E分别为AB,AC上的点,且
AB·AD=AC·AE,那么∠ADE的度数
是
90°
B
D
A
(第6题图)
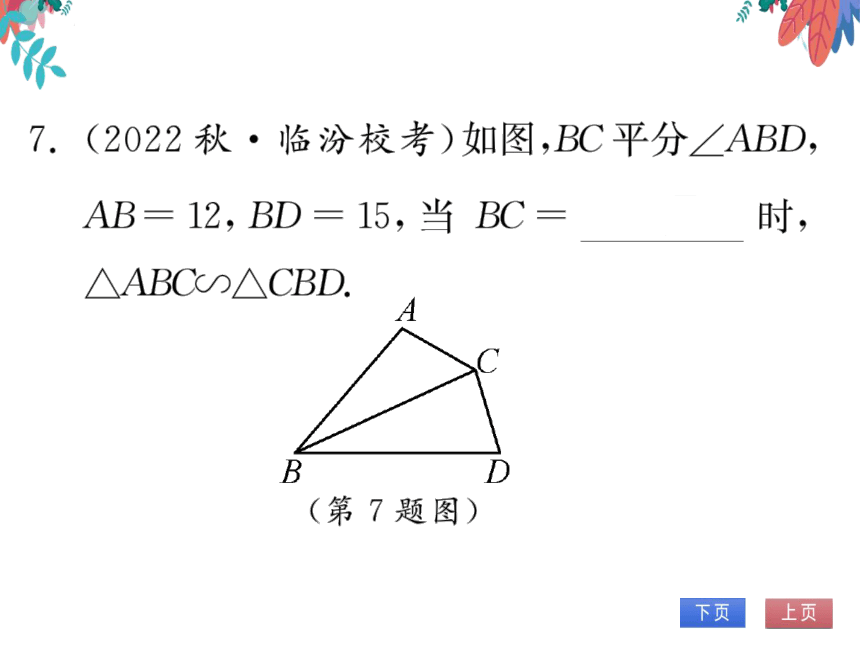
7.(2022秋·临汾校考)如图,BC平分∠ABD
AB=12,BD=15,当BC=6√5
时,
ΛABC∽△CBD.
A
B
D
(第7题图)
8.(2022秋·保定期末)如图,在正方形
ABCD中,点E,F分别是边AD,CD上的
点.AB-ED.D-IC,连接Er并延长
交BC的延长线于点G.
(1)求证:△ABEの△DEF;
(2)若正方形ABCD的边长为8,求BG
的长.
DF
解:(1)由题意得
DE
AE
2,又∠D=
/A
B
C
AB
=90°,.°。∧ABE刀人DEF.
(2)D57,∴△DEfn△(H,
DF
3.CG=3ED=12,.BC=8十12=20
27.2.1 相似三角形的判定
第3课时 相似三角形判定定理2
第二十七章 相似
必
●
知识要点全练
夯实基础
知识点1
两边成比例且夹角相等的两个三
角形相似
1.
(2022秋·四平期末)如图,四边形ABCD的
对角线AC、BD相交于O,且将这个四边形分
成①、②、③、④四个三角形,若OA:OC=OB:
OD,则下列结论中一定正确的是
B
A
y
B
3
C
(第1题图)
2.(2023春·信阳校考)如图,在△ABC中,
点D在边AC上,根据下列条件,能说明
△BDC∽△ABC的是
(C)
A.AB·CB=CA·CD
B.AB·CD=BD·BC
C.BC2=AC·DC
D.BD2=CD·DA
C
D
B
A
(第2题图)
3.(2023·江西新余)已知:如图,梯形ABCD
中,AB∥DC,∠B=90°,AB=3,BC=11,
DC=6.在线段BC上若存在点P,使得
△ABP与△PCD相似,则满足条件的P
点的个数为
B
A.4
B.3
C.2
D.1
D
A
B
C
(第3题图)
4.(2023春·周口期末)已知
↑
8
点A,B,C,D的坐标如图
所示,若要使以点C,D,E
4
3
为顶点的三角形与△ABC
B
C
D
相似,则点E的坐标不可
01234567x
以是
(B)
A.(6,0)
B.(6
,3)C.(6,5)D.(4,2)
A
5.如图,在△ABC和△ADE
AE
B元-ED
要
使△ABC与△ADE相似,还需要添加一个
条件,这个条件是
∠B=∠AED(答案不
唯一)
A
B
E
C
(第5题图)
6.(2023·江门模拟)如图,在∧ABC中,
∠C=90°,D,E分别为AB,AC上的点,且
AB·AD=AC·AE,那么∠ADE的度数
是
90°
B
D
A
(第6题图)
7.(2022秋·临汾校考)如图,BC平分∠ABD
AB=12,BD=15,当BC=6√5
时,
ΛABC∽△CBD.
A
B
D
(第7题图)
8.(2022秋·保定期末)如图,在正方形
ABCD中,点E,F分别是边AD,CD上的
点.AB-ED.D-IC,连接Er并延长
交BC的延长线于点G.
(1)求证:△ABEの△DEF;
(2)若正方形ABCD的边长为8,求BG
的长.
DF
解:(1)由题意得
DE
AE
2,又∠D=
/A
B
C
AB
=90°,.°。∧ABE刀人DEF.
(2)D57,∴△DEfn△(H,
DF
3.CG=3ED=12,.BC=8十12=20
