【同步精讲-习题课件】第27章《相似》27.2.1 第4课时 相似三角形判定定理3-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第27章《相似》27.2.1 第4课时 相似三角形判定定理3-人教版数学九下 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:50 | ||
图片预览





文档简介
(共22张PPT)
27.2.1 相似三角形的判定
第4课时 相似三角形判定定理3
第二十七章 相似
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
两角分别相等的两个三角形相似
1.已知一个三角形的两个内角分别是40°,
60°,另一个三角形的两个内角分别是40°,
80°,则这两个三角形
(
C
A.一定不相似
B.不一定相似
C.一定相似
D.不能确定
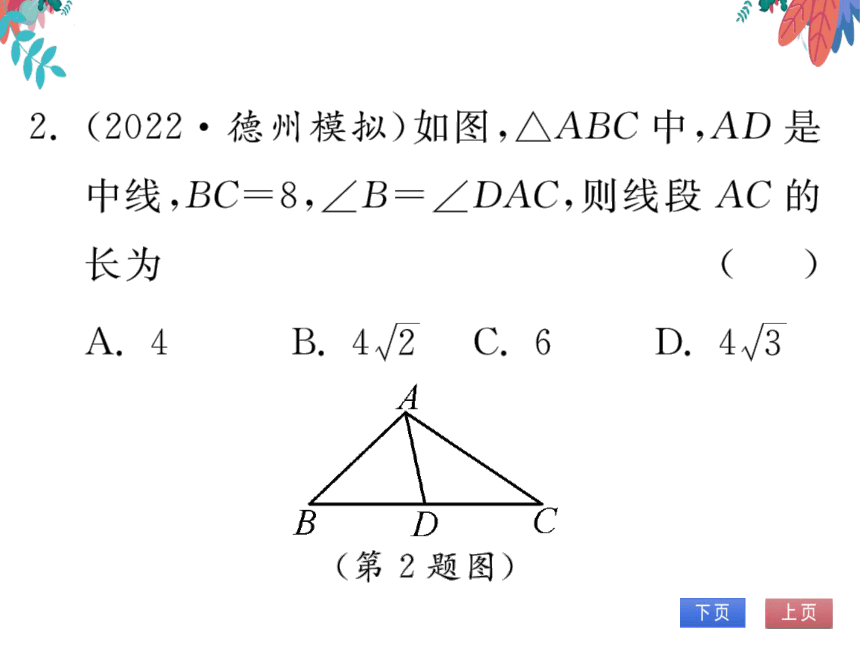
2.(2022·德州模拟)如图,△ABC中,AD是
中线,BC=8,∠B=∠DAC,则线段AC的
长为
(B)
A.4
B.4√/2
C.6
D.4W/3
B
D
C
(第2题图)
3.(2023春·恩施期末)如图,点D,E分别在
△ABC的AB,AC边上,增加下列条件中的一
个:①∠AED=B,四/AIDE=∠C,③AR
D
AD
AE
BC:④AC
;⑤AC=AD·AE,能使
△ADE与△ACB一定相似的有
(A)
A.①②④
B.
②④⑤
C.①②
0(4
D.①②
③⑤
E
B
C
(第3题图)
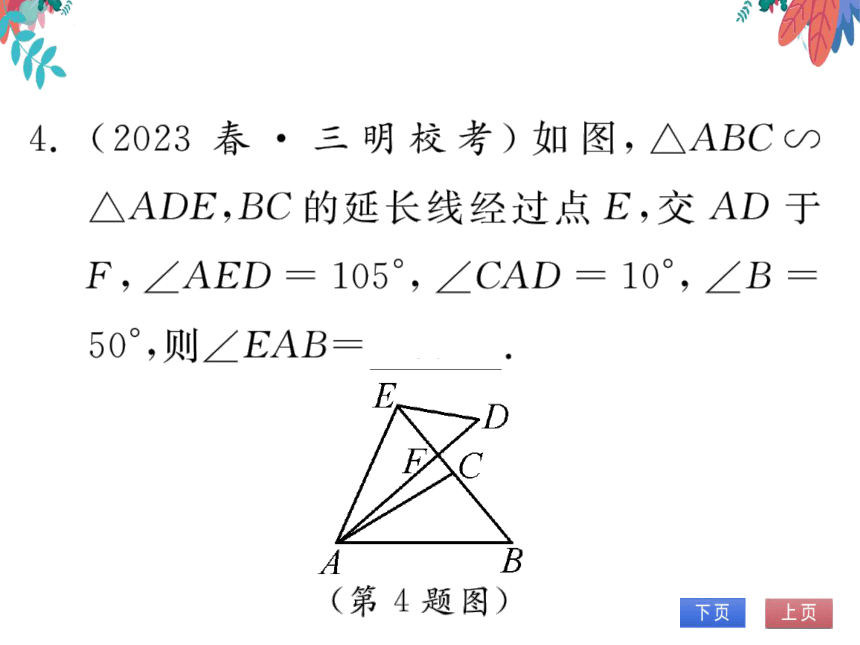
4.(2023春·三明校考)如图,人ABCの
△ADE,BC的延长线经过点E,交AD于
F,∠AED=105°,∠CAD=10°,∠B=
50°,则∠EAB
=
60°
E
D
C
A
B
(第4题图)
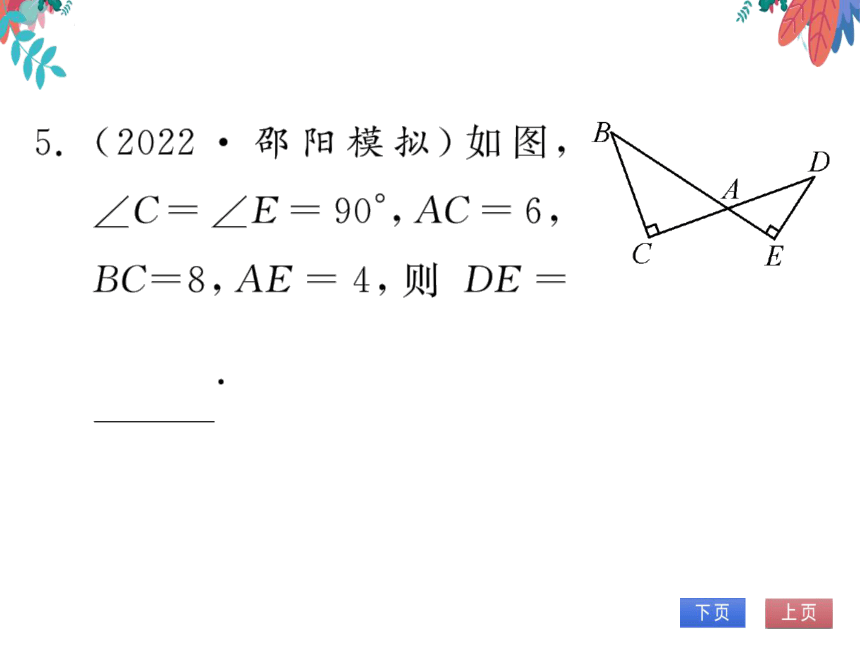
5.(2022·邵阳模拟)如图,B
∠C=∠E=90°,AC=6,
E
BC=8,AE=4,则DE=
16
3
6.(2023春·渭南校芳)如图,在△ABC中,
∠ABC=80°,∠BAC=40°,AB的垂直平
分线分别与AC,AB相交于点D,E,连接
BD,求证:△ABCの△BDC.
证明:。°DE是AB的垂直平分线,
。AD=BD,。°∠BAC=40°,.
∠ABD=40°,.·∠ABC=80°,
∠DBC=40°,.∠DBC=∠BAC,又.°∠C
=∠C,.'.∧ABCの△BDC.
知识点2直角三角形相似的判定
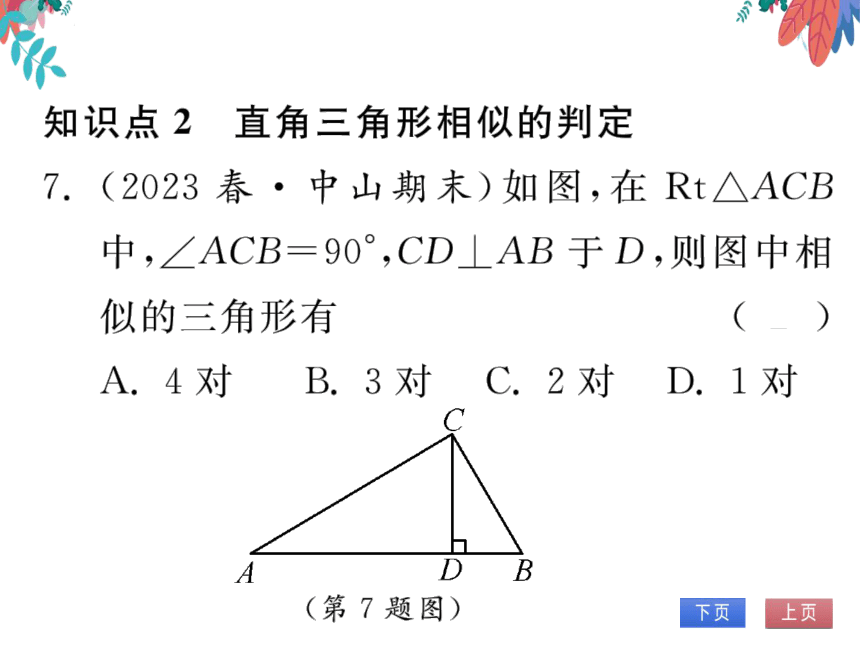
7.(2023春·中山期末)如图,在Rt△ACB
中,∠ACB=90°,CD⊥AB于D,则图中相
似的三角形有
(B
A.4对
B.3对
C.2对
D.1对
C
A
D
B
(第7题图)
8.(2023春·成都校考)如图,四边形ABCD
是矩形,E点在AD上,F点在DC上,且
∠BEF=90°,则三角形I,Ⅱ,Ⅲ,V中一
定相似的是
(B)
A.I和Ⅲ
B.I和IV
C.Ⅱ和Ⅲ
D.Ⅲ和V
27.2.1 相似三角形的判定
第4课时 相似三角形判定定理3
第二十七章 相似
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
两角分别相等的两个三角形相似
1.已知一个三角形的两个内角分别是40°,
60°,另一个三角形的两个内角分别是40°,
80°,则这两个三角形
(
C
A.一定不相似
B.不一定相似
C.一定相似
D.不能确定
2.(2022·德州模拟)如图,△ABC中,AD是
中线,BC=8,∠B=∠DAC,则线段AC的
长为
(B)
A.4
B.4√/2
C.6
D.4W/3
B
D
C
(第2题图)
3.(2023春·恩施期末)如图,点D,E分别在
△ABC的AB,AC边上,增加下列条件中的一
个:①∠AED=B,四/AIDE=∠C,③AR
D
AD
AE
BC:④AC
;⑤AC=AD·AE,能使
△ADE与△ACB一定相似的有
(A)
A.①②④
B.
②④⑤
C.①②
0(4
D.①②
③⑤
E
B
C
(第3题图)
4.(2023春·三明校考)如图,人ABCの
△ADE,BC的延长线经过点E,交AD于
F,∠AED=105°,∠CAD=10°,∠B=
50°,则∠EAB
=
60°
E
D
C
A
B
(第4题图)
5.(2022·邵阳模拟)如图,B
∠C=∠E=90°,AC=6,
E
BC=8,AE=4,则DE=
16
3
6.(2023春·渭南校芳)如图,在△ABC中,
∠ABC=80°,∠BAC=40°,AB的垂直平
分线分别与AC,AB相交于点D,E,连接
BD,求证:△ABCの△BDC.
证明:。°DE是AB的垂直平分线,
。AD=BD,。°∠BAC=40°,.
∠ABD=40°,.·∠ABC=80°,
∠DBC=40°,.∠DBC=∠BAC,又.°∠C
=∠C,.'.∧ABCの△BDC.
知识点2直角三角形相似的判定
7.(2023春·中山期末)如图,在Rt△ACB
中,∠ACB=90°,CD⊥AB于D,则图中相
似的三角形有
(B
A.4对
B.3对
C.2对
D.1对
C
A
D
B
(第7题图)
8.(2023春·成都校考)如图,四边形ABCD
是矩形,E点在AD上,F点在DC上,且
∠BEF=90°,则三角形I,Ⅱ,Ⅲ,V中一
定相似的是
(B)
A.I和Ⅲ
B.I和IV
C.Ⅱ和Ⅲ
D.Ⅲ和V
