【同步精讲-习题课件】第27章《相似》专题训练(六) 相似三角形的判定与性质-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第27章《相似》专题训练(六) 相似三角形的判定与性质-人教版数学九下 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:50 | ||
图片预览






文档简介
(共30张PPT)
专题训练(六) 相似三角形的判定与性质
第二十七章 相似
必
●
类型1
相似三角形的判定
1.(2022·徐州模拟)如图,在正方形ABCD
中,E是CD的中点,点F在BC上,且
FC-
BC.图中相似三角形共有
A.1对
B.2对
C.3对
D.4对
A
D
E
B
FC
(第1题图)
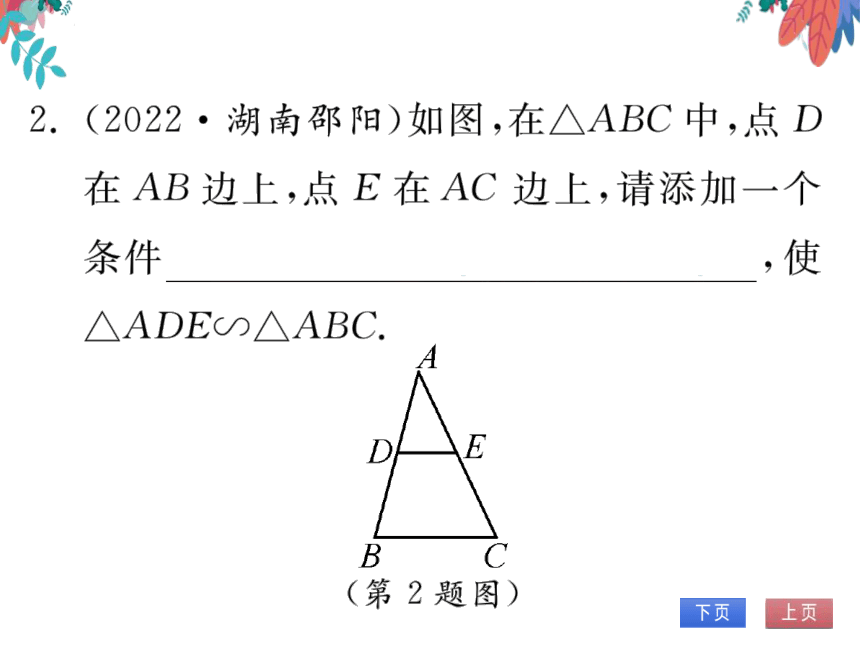
2.(2022·湖南邵阳)如图,在△ABC中,点D
在AB边上,点E在AC边上,请添加一个
条件
∠ADE=∠B(答案不唯一),使
△ADEの△ABC.
D
E
B
C
(第2题图)
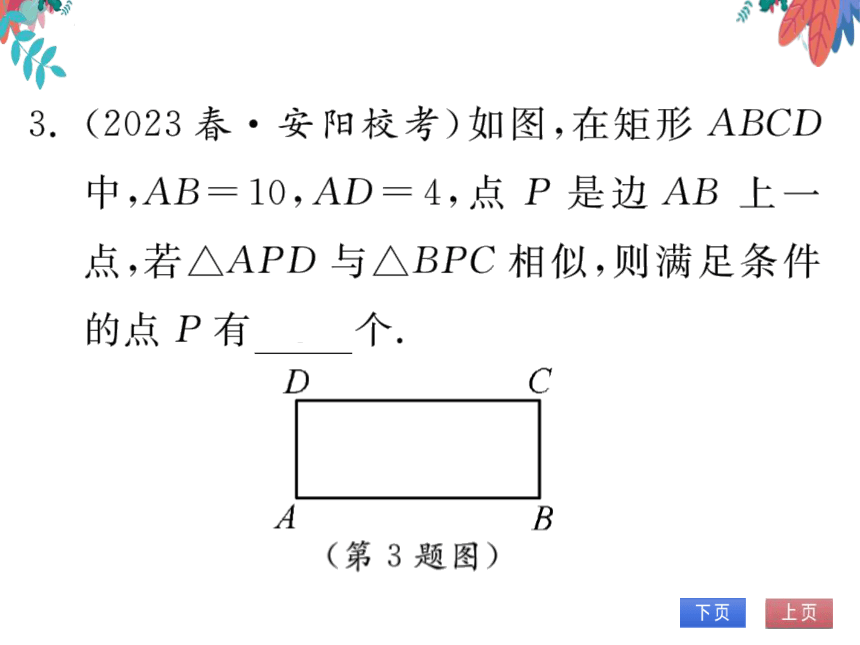
3.(2023春·安阳校考)如图,在矩形ABCD
中,AB=10,AD=4,点P是边AB上一
点,若△APD与△BPC相似,测满足条件
的点P有3个.
D
C
A
B
(第3题图)
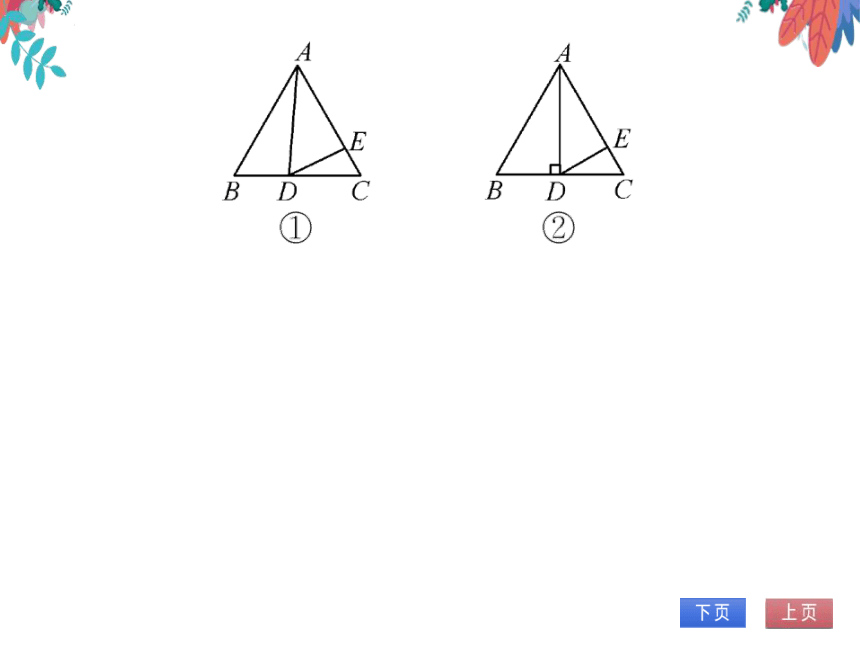
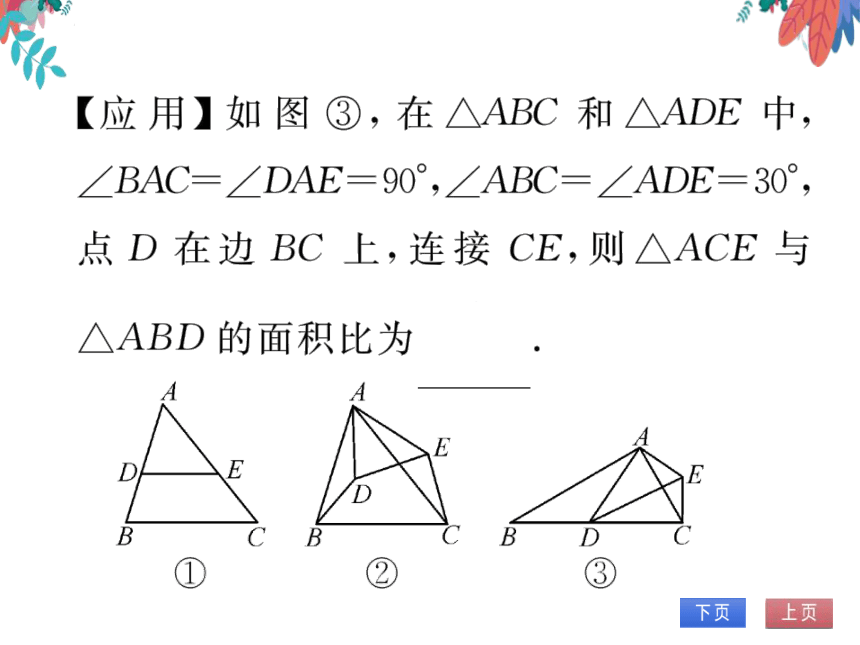
4.(2023春·秦皇岛期末)如图①,△ABC为
等边三角形,AB=20,点D为BC边上的
动点(点D不与点B,C重合),且∠ADE=
∠B,交AC边于点E.
(1)求证:△ABDの△DCE
(2)如图②,当D运动到BC的中点时,求
线段CE的值;
B
D
B
2
(1)证明:,三角形ABC是等边三角形,.∠D
=∠C=60°,,/ADC=/B十/BAD,/ADC
=/ADE十∠CDE,..∠B十∠BAD=∠ADE十
∠CDE,.∠ADE=∠D,.∠BAD=∠CDE,,
∠B=∠C,.'.∧AbDXの∧DCE;
(2)解:。°入ABC是等边三角形,点D是BC
中点,AD BC,BD=CD=I
2
BC=10,.
/ADC=90°,,ADE=60°,,.∠CDE=
30°,∴/DEC=90°,.CE=,CD=5.
2
类型2
相似三角形的性质
5.(2022·泰州模拟)如图,平行四边形ABCD
中,E是BC上的一点,且AB=BE,AE、DC
的延长线相交于点F,SAABE·S四边形AcD=3:7,
若AD=5cm,则CF的长为
D
A.1 cm
B.1.2 cm C.3 cm
2
cm
A
D
B
E
C
F
(第5题图)
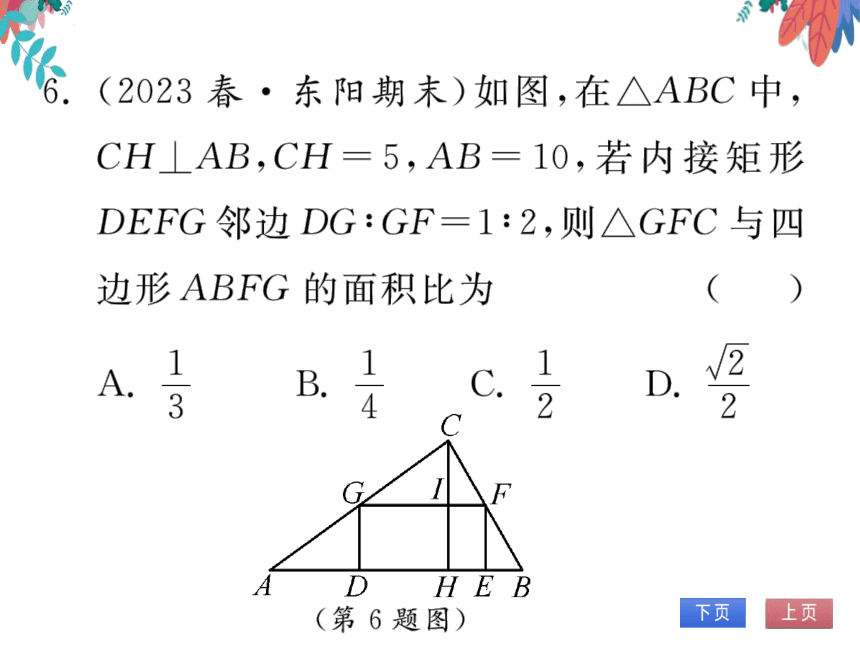
6.(2023春·东阳期末)如图,在△ABC中,
CH⊥AB,CH=5,AB=10,若内接矩形
DEFG邻边DG:GF=1:2,则△GFC与四
边形ABFG的面积比为
(A)
A.
1
B.
1
G
D
3
4
2
2
C
G
I
A
D
HE B
(第6题图)
专题训练(六) 相似三角形的判定与性质
第二十七章 相似
必
●
类型1
相似三角形的判定
1.(2022·徐州模拟)如图,在正方形ABCD
中,E是CD的中点,点F在BC上,且
FC-
BC.图中相似三角形共有
A.1对
B.2对
C.3对
D.4对
A
D
E
B
FC
(第1题图)
2.(2022·湖南邵阳)如图,在△ABC中,点D
在AB边上,点E在AC边上,请添加一个
条件
∠ADE=∠B(答案不唯一),使
△ADEの△ABC.
D
E
B
C
(第2题图)
3.(2023春·安阳校考)如图,在矩形ABCD
中,AB=10,AD=4,点P是边AB上一
点,若△APD与△BPC相似,测满足条件
的点P有3个.
D
C
A
B
(第3题图)
4.(2023春·秦皇岛期末)如图①,△ABC为
等边三角形,AB=20,点D为BC边上的
动点(点D不与点B,C重合),且∠ADE=
∠B,交AC边于点E.
(1)求证:△ABDの△DCE
(2)如图②,当D运动到BC的中点时,求
线段CE的值;
B
D
B
2
(1)证明:,三角形ABC是等边三角形,.∠D
=∠C=60°,,/ADC=/B十/BAD,/ADC
=/ADE十∠CDE,..∠B十∠BAD=∠ADE十
∠CDE,.∠ADE=∠D,.∠BAD=∠CDE,,
∠B=∠C,.'.∧AbDXの∧DCE;
(2)解:。°入ABC是等边三角形,点D是BC
中点,AD BC,BD=CD=I
2
BC=10,.
/ADC=90°,,ADE=60°,,.∠CDE=
30°,∴/DEC=90°,.CE=,CD=5.
2
类型2
相似三角形的性质
5.(2022·泰州模拟)如图,平行四边形ABCD
中,E是BC上的一点,且AB=BE,AE、DC
的延长线相交于点F,SAABE·S四边形AcD=3:7,
若AD=5cm,则CF的长为
D
A.1 cm
B.1.2 cm C.3 cm
2
cm
A
D
B
E
C
F
(第5题图)
6.(2023春·东阳期末)如图,在△ABC中,
CH⊥AB,CH=5,AB=10,若内接矩形
DEFG邻边DG:GF=1:2,则△GFC与四
边形ABFG的面积比为
(A)
A.
1
B.
1
G
D
3
4
2
2
C
G
I
A
D
HE B
(第6题图)
