【同步精讲-习题课件】第28章《锐角三角函数》28.1 第1课时 锐角的正弦-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第28章《锐角三角函数》28.1 第1课时 锐角的正弦-人教版数学九下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
28.1 锐角三角函数
第1课时 锐角的正弦
第二十八章 锐角三角函数
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
已知边长求正弦值
1.(2023·长宁模拟)在△ABC中,∠C=90°,
已知AC=3,AB=5,那么∠A的余弦值为
(
C
3
3
4
A.
B.
3
c
D.
4
5
5
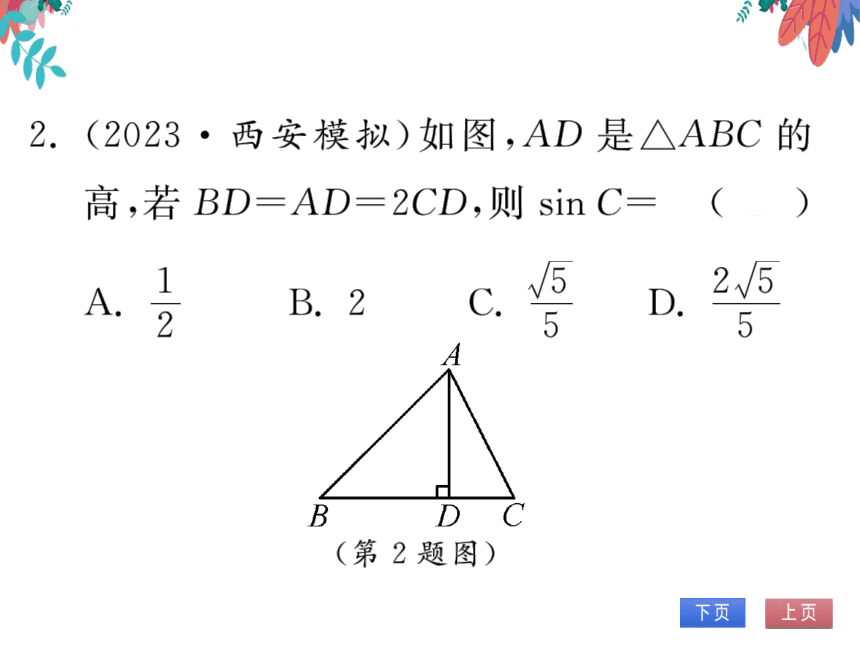
2.(2023·西安模拟)如图,AD是人ABC的
高,若BD=AD=2CD,则sinC=
(D)
1
A.
B.2
C.¥
5
D.
2/5
2
5
5
B
D
C
(第2题图)
3.(2023春·大庆期末)如图,在2×2正方形
网格(小正方形的边长均为1)中,△ABC
的顶点均在格点上,则sn∠CAB=
(B)
A.
B.
c.
/10
3
5
D
5
10
C
A
(第3题图)
4.在Rt△ABC中,∠C=90°,5AB=7BC,则sinB
的值为
2√6
7
5.(2023·佛山模拟)如图,在边长为1的正
方形网格中,点A,B,D在格点上,以AB
为直径的圆过C,D两点,则sin∠BCD的
3
值为
5
(第5题图)
知识点2
已知正弦值求边长
6.如图,在Rt△ABC中,∠C=90°,sinB=0.5,若
AC=6,则BC的长为
(C)
B
C
(第6题图)
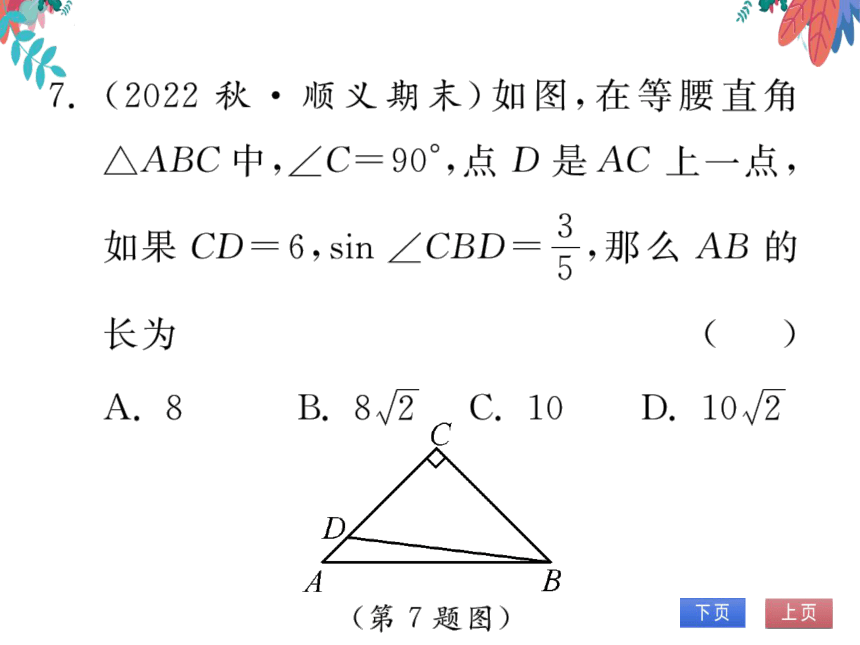
7.(2022秋·顺义期末)如图,在等腰直角
△ABC中,∠C=90°,点D是AC上一点,
如果CD-6,sin∠CBD-号那么AB的
长为
(B)
A.8
B.8√2
C.10
D.10√/2
C
A
B
(第7题图)
8.(2023春·南阳期末)如图所示,点A(t,3)
在第一象限,射线OA与x轴所夹的锐角
为a,sina=
则:的行为
√7
O
X
(第8题图)
9.(2022秋·绍兴校考)如图,△ABC内接于
⊙O,AB=AC,连接AO,CO.若BC=6,
sim∠I3A=.则⊙0的半径为5_·
A
B
C
(第9题图)
10.如图,在Rt△ABC中,∠C=90°,sinA=
3若AC=24,求△ABC的周长.
解:,sinA=
BC
AB
13
。'。可设BC=5x,AB=13x.
。°。AC=12x=24.。。x=2.
C
B
。°.BC=5x=10,AB=13x=26.
.∴.C△=AB+BC+AC=26十10+24=60.
28.1 锐角三角函数
第1课时 锐角的正弦
第二十八章 锐角三角函数
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
已知边长求正弦值
1.(2023·长宁模拟)在△ABC中,∠C=90°,
已知AC=3,AB=5,那么∠A的余弦值为
(
C
3
3
4
A.
B.
3
c
D.
4
5
5
2.(2023·西安模拟)如图,AD是人ABC的
高,若BD=AD=2CD,则sinC=
(D)
1
A.
B.2
C.¥
5
D.
2/5
2
5
5
B
D
C
(第2题图)
3.(2023春·大庆期末)如图,在2×2正方形
网格(小正方形的边长均为1)中,△ABC
的顶点均在格点上,则sn∠CAB=
(B)
A.
B.
c.
/10
3
5
D
5
10
C
A
(第3题图)
4.在Rt△ABC中,∠C=90°,5AB=7BC,则sinB
的值为
2√6
7
5.(2023·佛山模拟)如图,在边长为1的正
方形网格中,点A,B,D在格点上,以AB
为直径的圆过C,D两点,则sin∠BCD的
3
值为
5
(第5题图)
知识点2
已知正弦值求边长
6.如图,在Rt△ABC中,∠C=90°,sinB=0.5,若
AC=6,则BC的长为
(C)
B
C
(第6题图)
7.(2022秋·顺义期末)如图,在等腰直角
△ABC中,∠C=90°,点D是AC上一点,
如果CD-6,sin∠CBD-号那么AB的
长为
(B)
A.8
B.8√2
C.10
D.10√/2
C
A
B
(第7题图)
8.(2023春·南阳期末)如图所示,点A(t,3)
在第一象限,射线OA与x轴所夹的锐角
为a,sina=
则:的行为
√7
O
X
(第8题图)
9.(2022秋·绍兴校考)如图,△ABC内接于
⊙O,AB=AC,连接AO,CO.若BC=6,
sim∠I3A=.则⊙0的半径为5_·
A
B
C
(第9题图)
10.如图,在Rt△ABC中,∠C=90°,sinA=
3若AC=24,求△ABC的周长.
解:,sinA=
BC
AB
13
。'。可设BC=5x,AB=13x.
。°。AC=12x=24.。。x=2.
C
B
。°.BC=5x=10,AB=13x=26.
.∴.C△=AB+BC+AC=26十10+24=60.
