【同步精讲-习题课件】第28章《锐角三角函数》28.2.2 第1课时 与视角有关的实际问题-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第28章《锐角三角函数》28.2.2 第1课时 与视角有关的实际问题-人教版数学九下 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:50 | ||
图片预览




文档简介
(共19张PPT)
28.2.2 应用举例
第1课时 与视角有关的实际问题
第二十八章 锐角三角函数
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1与实际生活有关的实际问题
1.(2023·温州模拟)一张小凳子的结构如图
所示,AC=BC,∠1=100°,BC=20cm,则
AB等于
B
A.20sin50°cm
B.40cos50°cm
20
40
C,
sin50°
cm
D.
cos50°
cm
A
2
B
1
C
(第1题图)
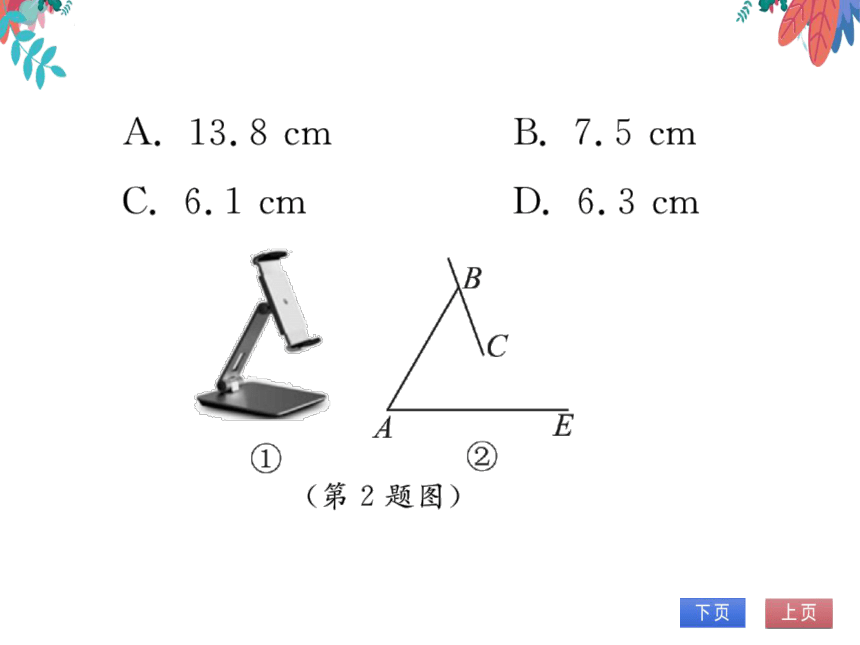
2.(2022·平顶山模拟)如图①是一台手机支
架,图②是其侧面示意图,AB,BC可分别
绕点A,B转动,测量知BC=8cm,AB=
16cm.当AB,BC转动到∠BAE=60°,
∠ABC=50°时,点C到AE的距离是
(D)(结果保留小数点后一位,参考数据:
sin70°≈0.94,W/3≈1.73)
B
C
A
E
1
2
(第2题图)
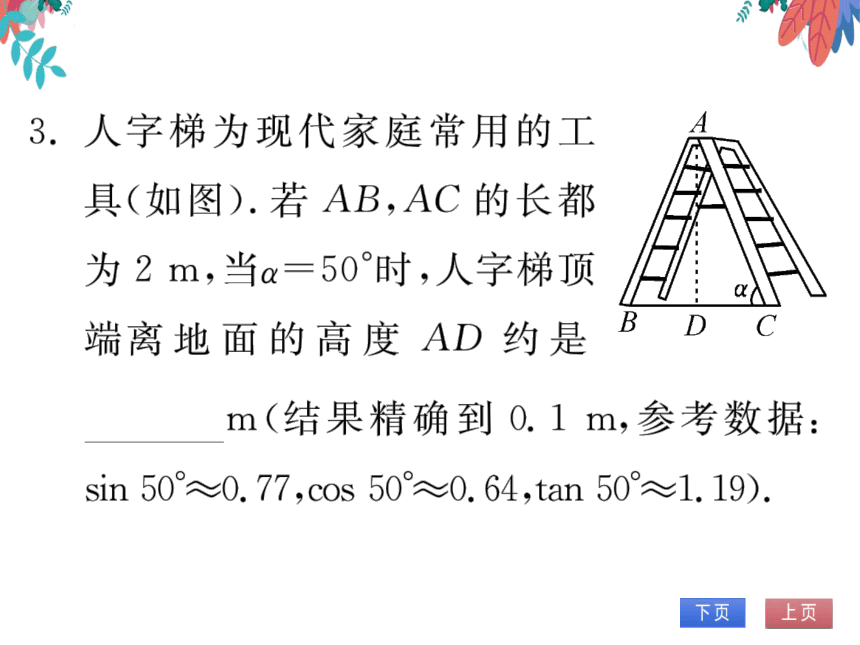
3.人字梯为现代家庭常用的工
具(如图).若AB,AC的长都
为2m,当α=50°时,人字梯顶
端离地面的高度AD约是
B
1.5m(结果精确到0.1m,参考数据:
sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
知识点2
与视角有关的实际问题
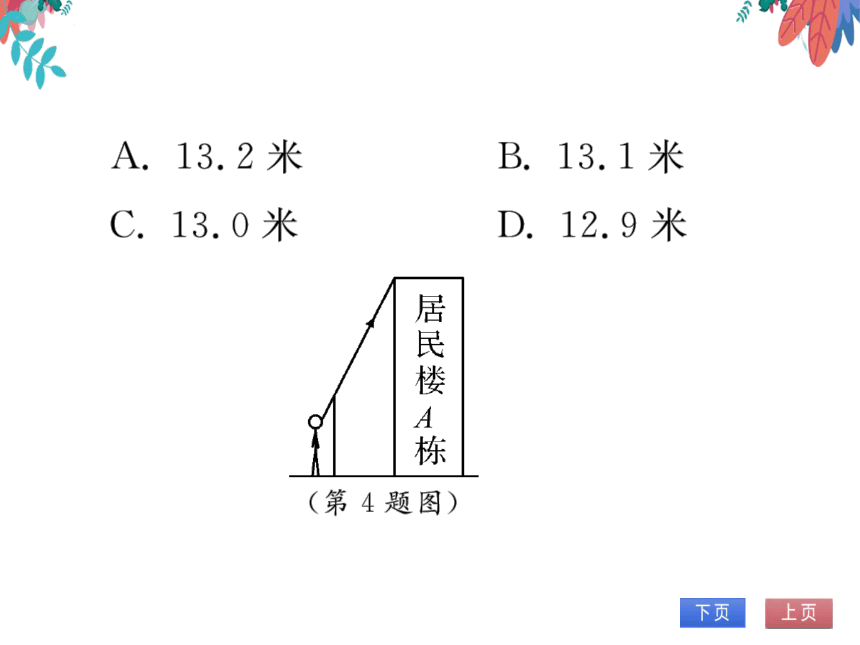
4.(2023·福州模拟)涂涂住在幸福小区.一
天,涂涂从小区外墙1米处以大约63.4°的
仰角看外墙的最高处(如图所示),此时他
的视线也恰好可以看到居民楼A栋的最高
处.若涂涂身高1.8米,居民楼A栋高
30米,则外墙距离居民楼A栋大约(D)(参
考数据:sin26.6°≈0.448,cos26.6°≈≈
0.894,tan26.6°^≈0.501)
居民楼A栋
(第4题图)
5.(2023春·长春期末)如图所示,热气球的
探测器显示,从热气球A处看一栋楼顶部
B处的仰角为30°,看这栋楼底部C处的俯
角为60°,热气球A处与楼的水平距离为
150m,则这栋楼的高度为
(C)
A.50√/3m
B.150/31
m
C.200/3m
D.300m
B
A
7777777777777
(第5题图)
6.(2023春·南宁校考)如图,某校数学“综合
与实践”小组采用无人机辅助的方法测量
南宁大桥的长度,测量过程中,小组成员遥
控无人机飞到桥AB的上方481米的点C
处悬停,此时测得桥上A,B两处的俯角分
别为30°和45°,则桥AB之间的距离为
28.2.2 应用举例
第1课时 与视角有关的实际问题
第二十八章 锐角三角函数
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1与实际生活有关的实际问题
1.(2023·温州模拟)一张小凳子的结构如图
所示,AC=BC,∠1=100°,BC=20cm,则
AB等于
B
A.20sin50°cm
B.40cos50°cm
20
40
C,
sin50°
cm
D.
cos50°
cm
A
2
B
1
C
(第1题图)
2.(2022·平顶山模拟)如图①是一台手机支
架,图②是其侧面示意图,AB,BC可分别
绕点A,B转动,测量知BC=8cm,AB=
16cm.当AB,BC转动到∠BAE=60°,
∠ABC=50°时,点C到AE的距离是
(D)(结果保留小数点后一位,参考数据:
sin70°≈0.94,W/3≈1.73)
B
C
A
E
1
2
(第2题图)
3.人字梯为现代家庭常用的工
具(如图).若AB,AC的长都
为2m,当α=50°时,人字梯顶
端离地面的高度AD约是
B
1.5m(结果精确到0.1m,参考数据:
sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
知识点2
与视角有关的实际问题
4.(2023·福州模拟)涂涂住在幸福小区.一
天,涂涂从小区外墙1米处以大约63.4°的
仰角看外墙的最高处(如图所示),此时他
的视线也恰好可以看到居民楼A栋的最高
处.若涂涂身高1.8米,居民楼A栋高
30米,则外墙距离居民楼A栋大约(D)(参
考数据:sin26.6°≈0.448,cos26.6°≈≈
0.894,tan26.6°^≈0.501)
居民楼A栋
(第4题图)
5.(2023春·长春期末)如图所示,热气球的
探测器显示,从热气球A处看一栋楼顶部
B处的仰角为30°,看这栋楼底部C处的俯
角为60°,热气球A处与楼的水平距离为
150m,则这栋楼的高度为
(C)
A.50√/3m
B.150/31
m
C.200/3m
D.300m
B
A
7777777777777
(第5题图)
6.(2023春·南宁校考)如图,某校数学“综合
与实践”小组采用无人机辅助的方法测量
南宁大桥的长度,测量过程中,小组成员遥
控无人机飞到桥AB的上方481米的点C
处悬停,此时测得桥上A,B两处的俯角分
别为30°和45°,则桥AB之间的距离为
