【同步精讲-习题课件】第28章《锐角三角函数》28.2.2 第2课时 与方位角、坡角有关的实际问题-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第28章《锐角三角函数》28.2.2 第2课时 与方位角、坡角有关的实际问题-人教版数学九下 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:50 | ||
图片预览






文档简介
(共21张PPT)
28.2.2 应用举例
第2课时 与方位角、坡角有关的实际问题
第二十八章 锐角三角函数
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
与方位角有关的实际问题
1.(2023春·武汉校考)如图,北
一艘海轮位于灯塔P的南偏
东37°方向,距离灯塔35海里
的A处,它沿正北方向航行
一段时间后,到达位于灯塔正东方向上的
B处,这时,B处与灯塔P的距离PB的长
可以表示为
D
A.35海里
B.35c0s37海里
C.35tan37海里
D.35sin37°海里
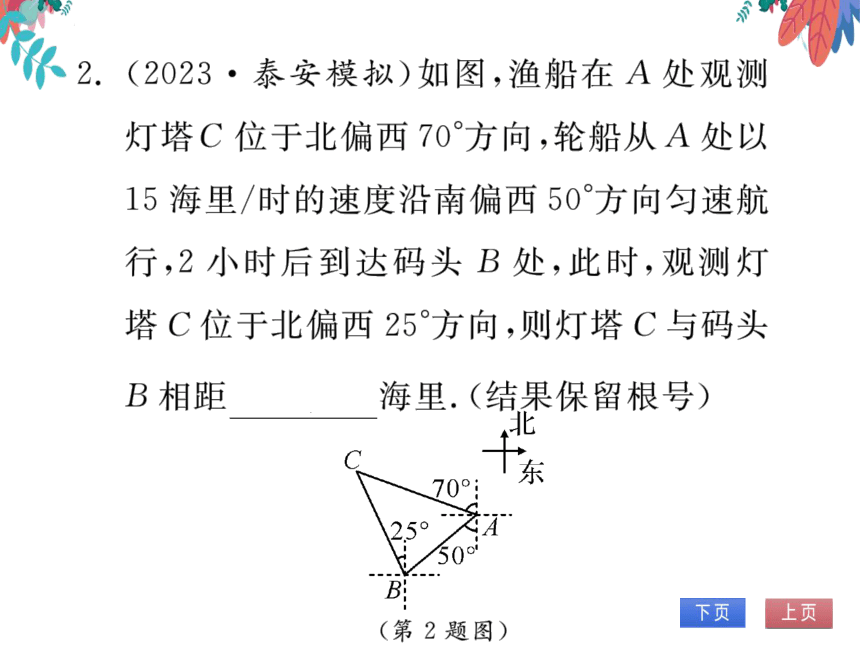
(2023·泰安模拟)如图,渔船在A处观测
2.
灯塔C位于北偏西70°方向,轮船从A处以
15海里/时的速度沿南偏西50°方向匀速航
行,2小时后到达码头B处,此时,观测灯
塔C位于北偏西25°方向,则灯塔C与码头
B相距
15√6海里.(结果保留根号)
C
(第2题图)
3.
(2022·四川巴中)一艘轮船位于灯塔P的
南偏东60°方向,距离灯塔30海里的A处,
它沿北偏东30°方向航行一段时间后,到达
位于灯塔P的北偏东67°方向上的B处,此
时与灯塔P的距离约为
50海里.(参芳数
据:sn375os7,tan37)
B
670
60ò
A
(第3题图)
知识点2与坡度有关的实际问题
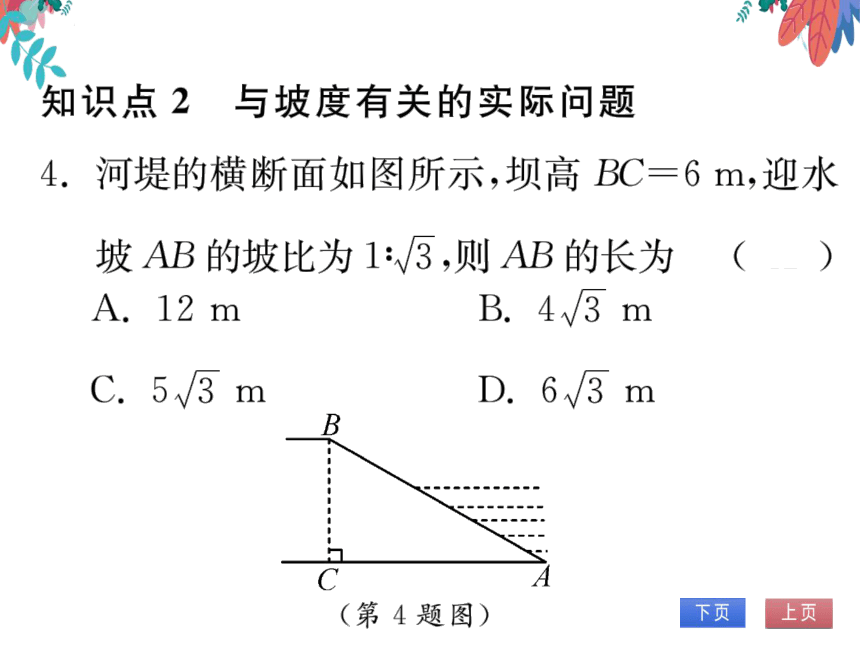
4.河堤的横断面如图所示,坝高BC=6m,迎水
坡AB的坡比为1:√3,则AB的长为
A
B
C
A
(第4题图)
5.(2023春·黄石校考)如图,已知点C与某
建筑物底端B相距306米(点C与点B在
同一水平面上),某同学从点C出发,沿同
一剖面的斜坡CD行走195米至坡顶D
处,斜坡CD的坡度(或坡比)i=1:2.4,在
D处测得该建筑物顶端A的俯角为20°,则
建筑物AB的高度约为(精确到0.1米,参
考数据:sin20°≈0.342,c0s20°≈0.940,
tan20°^≈0.364)
(A)
A.29.1米
B.31.9米
C.45.9米
D.95.9米
i=1:2.4
D
C
B
(第5题图)
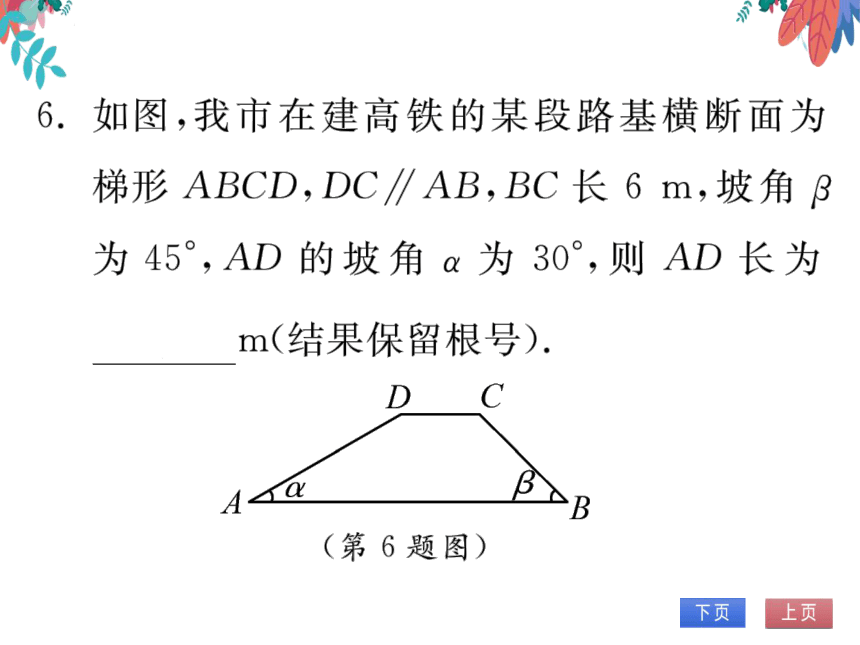
6.如图,我市在建高铁的某段路基横断面为
梯形ABCD,DC∥AB,BC长6m,坡角3
为45°,AD的坡角a为30°,则AD长为
6√2
m(结果保留根号).
A
B
C
i=1:0.75
D
E
(第7题图)
28.2.2 应用举例
第2课时 与方位角、坡角有关的实际问题
第二十八章 锐角三角函数
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
与方位角有关的实际问题
1.(2023春·武汉校考)如图,北
一艘海轮位于灯塔P的南偏
东37°方向,距离灯塔35海里
的A处,它沿正北方向航行
一段时间后,到达位于灯塔正东方向上的
B处,这时,B处与灯塔P的距离PB的长
可以表示为
D
A.35海里
B.35c0s37海里
C.35tan37海里
D.35sin37°海里
(2023·泰安模拟)如图,渔船在A处观测
2.
灯塔C位于北偏西70°方向,轮船从A处以
15海里/时的速度沿南偏西50°方向匀速航
行,2小时后到达码头B处,此时,观测灯
塔C位于北偏西25°方向,则灯塔C与码头
B相距
15√6海里.(结果保留根号)
C
(第2题图)
3.
(2022·四川巴中)一艘轮船位于灯塔P的
南偏东60°方向,距离灯塔30海里的A处,
它沿北偏东30°方向航行一段时间后,到达
位于灯塔P的北偏东67°方向上的B处,此
时与灯塔P的距离约为
50海里.(参芳数
据:sn375os7,tan37)
B
670
60ò
A
(第3题图)
知识点2与坡度有关的实际问题
4.河堤的横断面如图所示,坝高BC=6m,迎水
坡AB的坡比为1:√3,则AB的长为
A
B
C
A
(第4题图)
5.(2023春·黄石校考)如图,已知点C与某
建筑物底端B相距306米(点C与点B在
同一水平面上),某同学从点C出发,沿同
一剖面的斜坡CD行走195米至坡顶D
处,斜坡CD的坡度(或坡比)i=1:2.4,在
D处测得该建筑物顶端A的俯角为20°,则
建筑物AB的高度约为(精确到0.1米,参
考数据:sin20°≈0.342,c0s20°≈0.940,
tan20°^≈0.364)
(A)
A.29.1米
B.31.9米
C.45.9米
D.95.9米
i=1:2.4
D
C
B
(第5题图)
6.如图,我市在建高铁的某段路基横断面为
梯形ABCD,DC∥AB,BC长6m,坡角3
为45°,AD的坡角a为30°,则AD长为
6√2
m(结果保留根号).
A
B
C
i=1:0.75
D
E
(第7题图)
