【同步精讲-习题课件】第28章《锐角三角函数》本章重难点突破-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第28章《锐角三角函数》本章重难点突破-人教版数学九下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
本章重难点突破
第二十八章 锐角三角函数
必
●
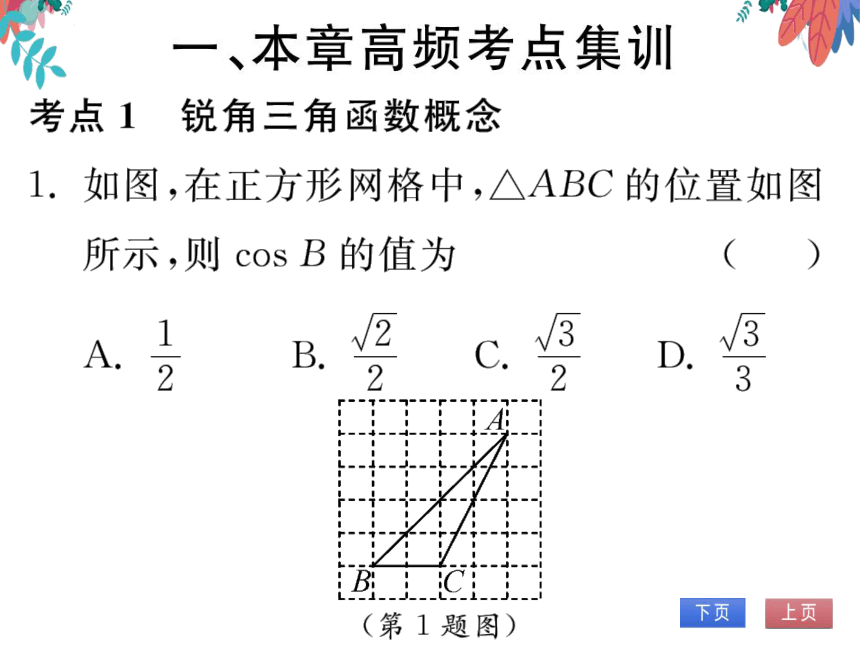
考点1锐角三角函数概念
1.如图,在正方形网格中,△ABC的位置如图
所示,则cosB的值为
B
A.
1
B.
c.
2
D
2
2
3
-
米
(第1题图)
2.(2023春·襄阳校考)直线y=kx一4与y
抽相交,所成的锐角的切值为2则的
值为
(C)
A.2
B.
-2
C.士2
D.无法确定
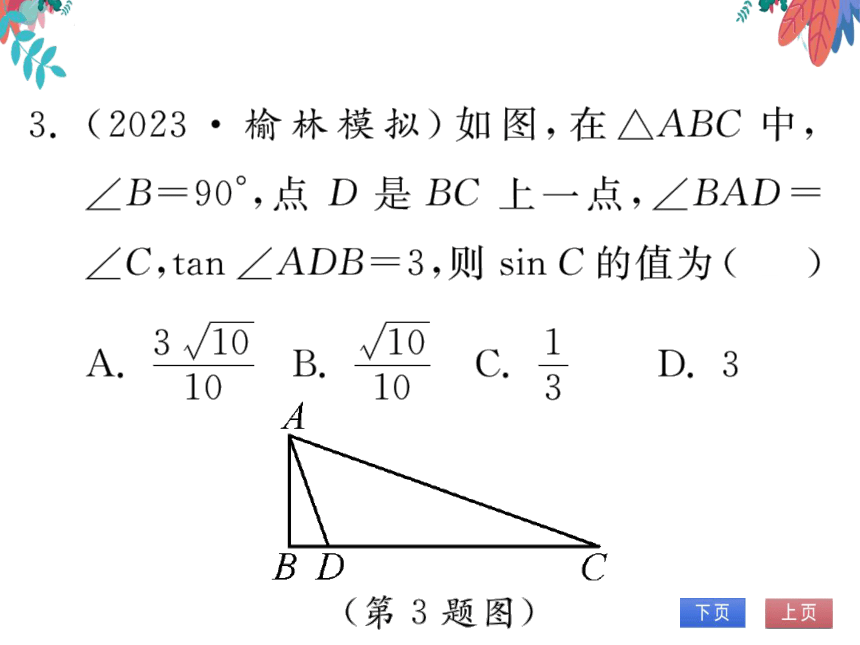
3.(2023·榆林模拟)如图,在△ABC中,
∠B=90°,点D是BC上一点,∠BAD=
∠C,tan∠ADB=3,则sinC的值为(Bb)
4,
3W10
B.10
C.
D.3
10
10
3
A
B D
C
(第3题图)
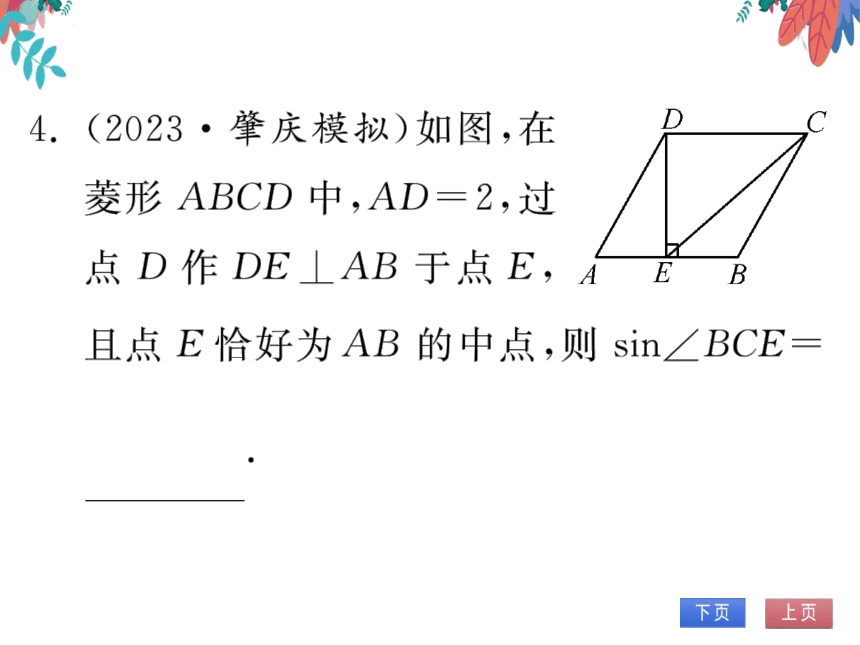
4.(2023·肇庆模拟)如图,在
菱形ABCD中,AD=2,过
点D作DE⊥AB于点E,A
E
B
且点E恰好为AB的中点,则sin∠BCE=
W21
14
考点2特殊角的三角函数值
5.(2022秋·邯郸校考)点M(一sin60°,
c0s60°)关于y轴对称的点的坐标是(A)
A.(
c.(-
3
D.
6.(2023春·宜春期末)在ABC中,
(2cosA-√2)+1-tanB|=0,则
△ABC一定是
(D)
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
7.(2023·温州模拟)如图,直线y=一√3x十
3分别交x轴,y轴于点A,B,将△AOB绕
点O逆时针旋转至△COD,使点C落在
AB上,CD交y轴于点E.分别记△BCE,
△DEO的面积为S1,S2,则
的值为
1
3
B
D
E
C
ol
(第7题图)
考点3解直角三角形
8.
如图,在△ABC中,sinB=
3,tan C=2,
AB=3,则AC的长为
(B)
A.√/2
B.5
2
C.5
D.2
9.(2023·合肥模拟)如图,Rt△ABC中,
∠C=90°,点D在BC上,∠CDA=
∠CAB.若BC=4,tanB-
则AD时长
度为
(C)
D
A
B
9
12
15
A.
B.
5
C.
D.4
4
4
10.(2023·呼和浩特)如图,在平
面直角坐标系中,△OAB三
个顶点的坐标分别为O(0,
0),A(23,0),B(√3,1),△OAB与
△OAB关于直线OB对称,反比例函数
V-
k(k>0,C一0)的图象与AB交于点
C
C,若A'C=BC,则k的值为
A
A.23
B.
3√3
C.√3
D.
3
2
2
本章重难点突破
第二十八章 锐角三角函数
必
●
考点1锐角三角函数概念
1.如图,在正方形网格中,△ABC的位置如图
所示,则cosB的值为
B
A.
1
B.
c.
2
D
2
2
3
-
米
(第1题图)
2.(2023春·襄阳校考)直线y=kx一4与y
抽相交,所成的锐角的切值为2则的
值为
(C)
A.2
B.
-2
C.士2
D.无法确定
3.(2023·榆林模拟)如图,在△ABC中,
∠B=90°,点D是BC上一点,∠BAD=
∠C,tan∠ADB=3,则sinC的值为(Bb)
4,
3W10
B.10
C.
D.3
10
10
3
A
B D
C
(第3题图)
4.(2023·肇庆模拟)如图,在
菱形ABCD中,AD=2,过
点D作DE⊥AB于点E,A
E
B
且点E恰好为AB的中点,则sin∠BCE=
W21
14
考点2特殊角的三角函数值
5.(2022秋·邯郸校考)点M(一sin60°,
c0s60°)关于y轴对称的点的坐标是(A)
A.(
c.(-
3
D.
6.(2023春·宜春期末)在ABC中,
(2cosA-√2)+1-tanB|=0,则
△ABC一定是
(D)
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
7.(2023·温州模拟)如图,直线y=一√3x十
3分别交x轴,y轴于点A,B,将△AOB绕
点O逆时针旋转至△COD,使点C落在
AB上,CD交y轴于点E.分别记△BCE,
△DEO的面积为S1,S2,则
的值为
1
3
B
D
E
C
ol
(第7题图)
考点3解直角三角形
8.
如图,在△ABC中,sinB=
3,tan C=2,
AB=3,则AC的长为
(B)
A.√/2
B.5
2
C.5
D.2
9.(2023·合肥模拟)如图,Rt△ABC中,
∠C=90°,点D在BC上,∠CDA=
∠CAB.若BC=4,tanB-
则AD时长
度为
(C)
D
A
B
9
12
15
A.
B.
5
C.
D.4
4
4
10.(2023·呼和浩特)如图,在平
面直角坐标系中,△OAB三
个顶点的坐标分别为O(0,
0),A(23,0),B(√3,1),△OAB与
△OAB关于直线OB对称,反比例函数
V-
k(k>0,C一0)的图象与AB交于点
C
C,若A'C=BC,则k的值为
A
A.23
B.
3√3
C.√3
D.
3
2
2
