【同步精讲-习题课件】第28章《锐角三角函数》专题训练(十二) 锐角三角函数和圆-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第28章《锐角三角函数》专题训练(十二) 锐角三角函数和圆-人教版数学九下 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:50 | ||
图片预览






文档简介
(共36张PPT)
专题训练(十二) 锐角三角函数和圆
第二十八章 锐角三角函数
必
●
类型1在圆中求锐角三角函数的值
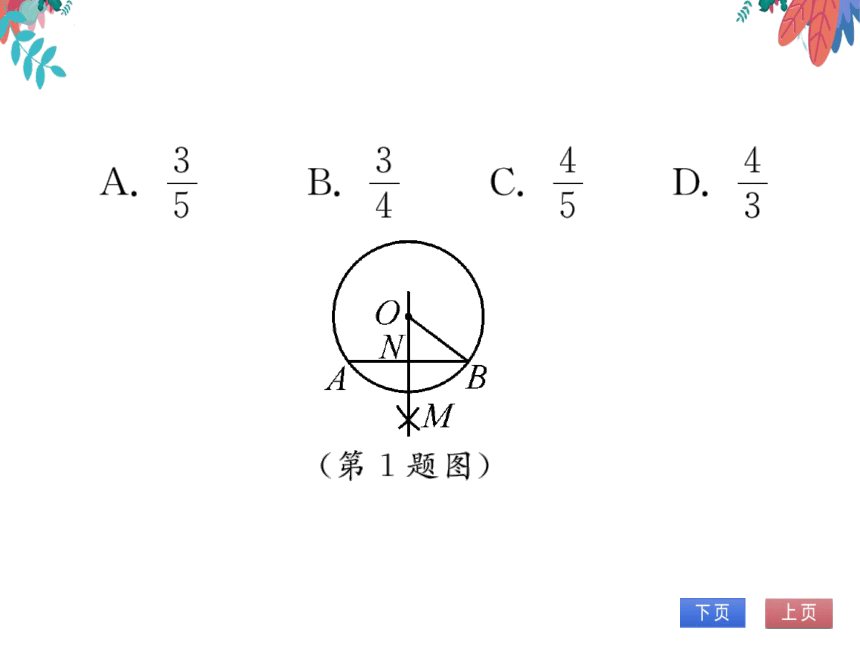
1.(2021·广西百色)如图,在⊙O中,尺规作
图的部分作法如下:(1)分别以弦AB的端
点A、B为圆心,适当等长为半径画弧,使
两弧相交于点M;(2)作直线OM交AB于
点N.若OB=10,AB=16,则tanB等于
B
O
N
A
B
米M
(第1题图)
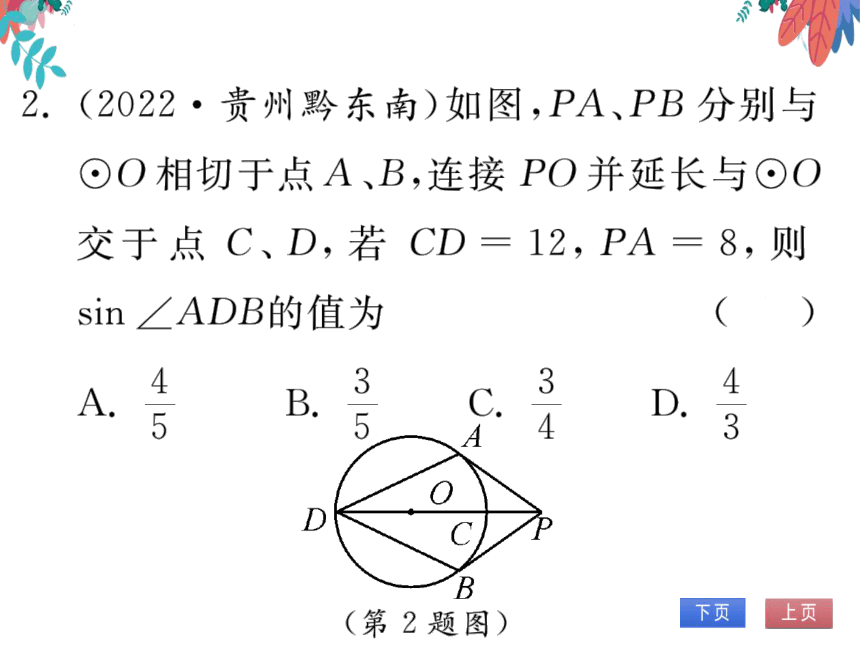
2.(2022·贵州黔东南)如图,PA、PB分别与
⊙O相切于点A、B,连接PO并延长与⊙0
交于点C、D,若
CD=12,PA=8,则
sin∠ADB的值为
A
4
3
3
4
A.
B.
C
D.
5
5
4
3
3.(2022·内蒙古通辽)如图,由边长为1的
小正方形构成的网格中,点A,B,C都在格
点上,以AB为直径的圆经过点C,D,则
cos∠ADC的值为
B
A,
2√13
B.33
C.
23
D.
13
13
3
(第3题图)
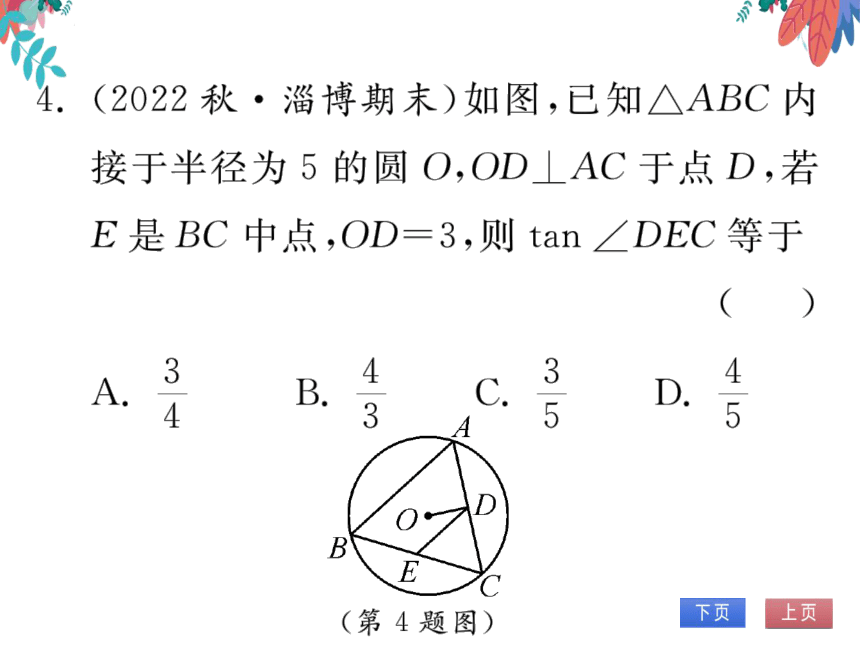
4.(2022秋·淄博期末)如图,已知△ABC内
接于半径为5的圆O,OD⊥AC于点D,若
E是BC中点,OD=3,则tan∠DEC等于
B
3
3
4
A.
B.
C.
5
D.
4
3
5
A
D
B
E
C
(第4题图)
5.(2023春·恩施校考)如图,AB为⊙O直
径,△ABC内接于⊙O,I为△ABC内心,
AI交于D,且OIAD于I,则
5
sin∠CAD的值为
5
A
B
C
D
(第5题图)
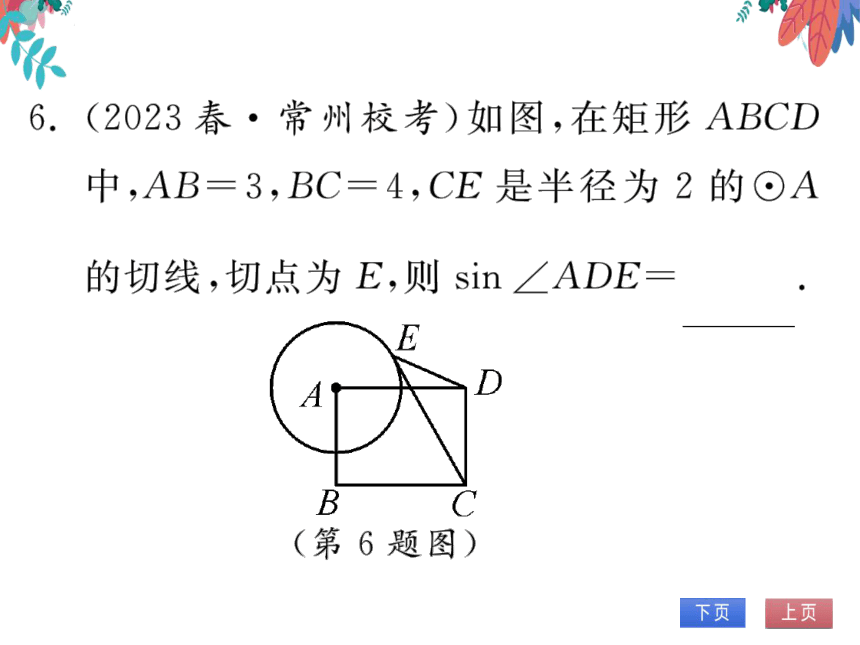
6.(2023春·常州校考)如图,在矩形ABCD
中,AB=3,BC=4,CE是半径为2的⊙A
2
的切线,切点为E,则sn∠ADE=
5
E
A
D
B
C
(第6题图)
7.(2023春·金华校考)如图,
AB是半圆O的直径,弦
B
AD,BC相交于点P,且CD,AB是一元二
次方程x2一10x+24=0的两根,则
2
cOS∠BPD是
3
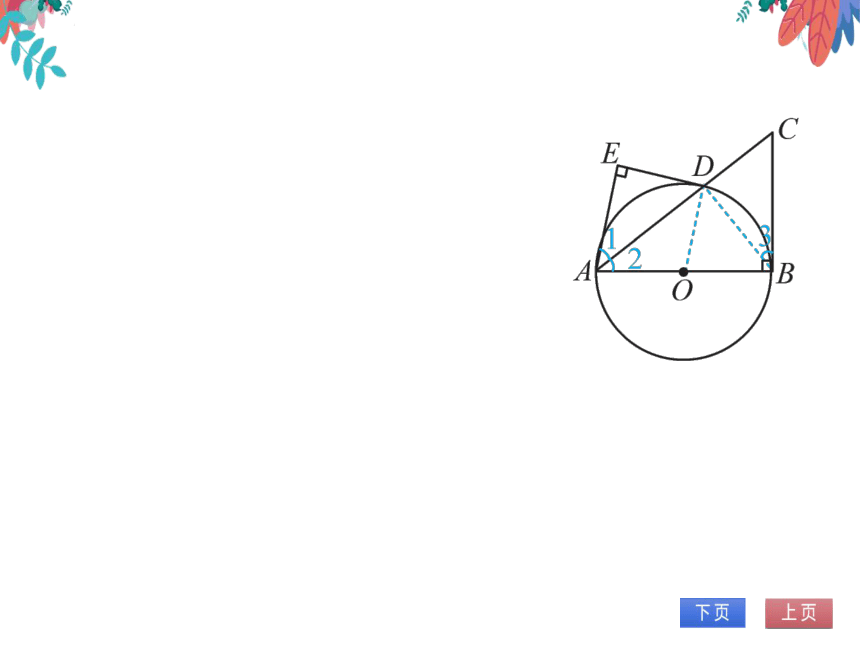
8.如图,在Rt△ABC中,∠ABC=90°,以AB
为直径的⊙O交AC于点D,AE与过点D
的切线互相垂直,垂足为E.
(1)求证:AD平分∠BAE;
(2)若CD=DE,求sin∠BAC的值.
(1)证明:如图,连接OD.。°DE为切
线,'.OD⊥DE..DE⊥E,.OD∥
AE..∠1=∠ODA..OA=OD,.∠2
B
ODA.
。∠1=∠2..AD平分∠BAE.
专题训练(十二) 锐角三角函数和圆
第二十八章 锐角三角函数
必
●
类型1在圆中求锐角三角函数的值
1.(2021·广西百色)如图,在⊙O中,尺规作
图的部分作法如下:(1)分别以弦AB的端
点A、B为圆心,适当等长为半径画弧,使
两弧相交于点M;(2)作直线OM交AB于
点N.若OB=10,AB=16,则tanB等于
B
O
N
A
B
米M
(第1题图)
2.(2022·贵州黔东南)如图,PA、PB分别与
⊙O相切于点A、B,连接PO并延长与⊙0
交于点C、D,若
CD=12,PA=8,则
sin∠ADB的值为
A
4
3
3
4
A.
B.
C
D.
5
5
4
3
3.(2022·内蒙古通辽)如图,由边长为1的
小正方形构成的网格中,点A,B,C都在格
点上,以AB为直径的圆经过点C,D,则
cos∠ADC的值为
B
A,
2√13
B.33
C.
23
D.
13
13
3
(第3题图)
4.(2022秋·淄博期末)如图,已知△ABC内
接于半径为5的圆O,OD⊥AC于点D,若
E是BC中点,OD=3,则tan∠DEC等于
B
3
3
4
A.
B.
C.
5
D.
4
3
5
A
D
B
E
C
(第4题图)
5.(2023春·恩施校考)如图,AB为⊙O直
径,△ABC内接于⊙O,I为△ABC内心,
AI交于D,且OIAD于I,则
5
sin∠CAD的值为
5
A
B
C
D
(第5题图)
6.(2023春·常州校考)如图,在矩形ABCD
中,AB=3,BC=4,CE是半径为2的⊙A
2
的切线,切点为E,则sn∠ADE=
5
E
A
D
B
C
(第6题图)
7.(2023春·金华校考)如图,
AB是半圆O的直径,弦
B
AD,BC相交于点P,且CD,AB是一元二
次方程x2一10x+24=0的两根,则
2
cOS∠BPD是
3
8.如图,在Rt△ABC中,∠ABC=90°,以AB
为直径的⊙O交AC于点D,AE与过点D
的切线互相垂直,垂足为E.
(1)求证:AD平分∠BAE;
(2)若CD=DE,求sin∠BAC的值.
(1)证明:如图,连接OD.。°DE为切
线,'.OD⊥DE..DE⊥E,.OD∥
AE..∠1=∠ODA..OA=OD,.∠2
B
ODA.
。∠1=∠2..AD平分∠BAE.
