【同步精讲-习题课件】第28章《锐角三角函数》专题训练(十一) 解直角三角形的基本策略-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第28章《锐角三角函数》专题训练(十一) 解直角三角形的基本策略-人教版数学九下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:50 | ||
图片预览








文档简介
(共30张PPT)
专题训练(十一) 解直角三角形的基本策略
第二十八章 锐角三角函数
必
●
类型1构造单一直角三角形解决问题
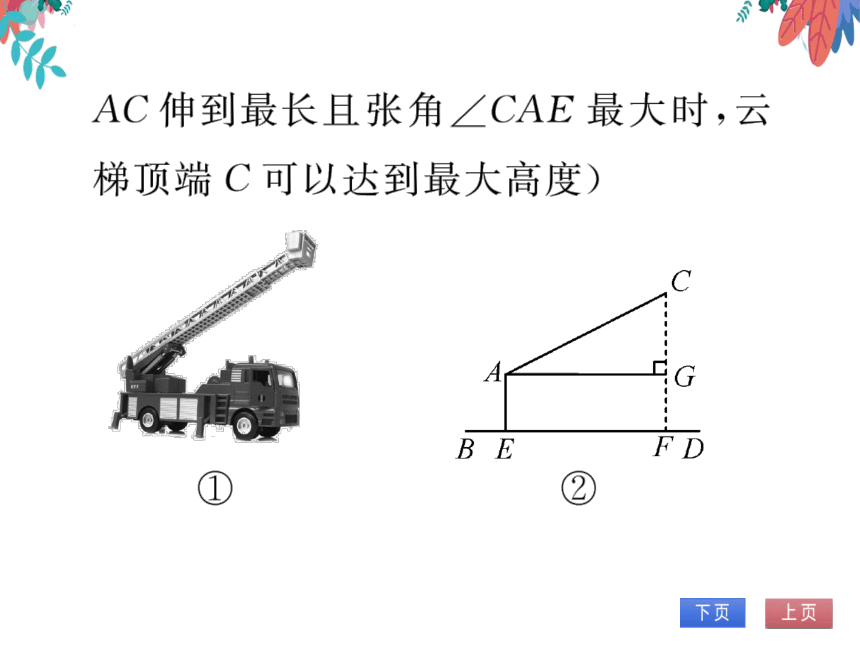
1.(2023·吉林模拟)消防车是救援火灾的主
要装备,图①是一辆登高云梯消防车的实
物图,图②是其工作示意图,起重臂AC
(20米≤AC≤30米)是可伸缩的,且起重
臂AC可绕点A在一定范围内上下转动张
角∠CAE(90°≤∠CAE≤150°),转动点A
距离地面的高度AE为4米.
(1)当起重臂AC的长度为24米,张角
∠CAE=120°时,登高云梯消防车最高点C
距离地面的高度CF的长为
16米.
(2)某日一栋大楼突发火灾,着火点距离地
面的高度为26米,该消防车在这栋楼
下能否实施有效救援?请说明理由.
(参考数据:√3≈1.7)(提示:当起重臂
AC伸到最长且张角∠CAE最大时,云
梯顶端C可以达到最大高度)
A
G
B E
①
②
解:(2)当起重臂最长,转动张角最大时,
即:AC=30米,∠CAE=150°,。∠CAG=
60°,.CG=AC·sin60°=30X
=15/3
2
≈25.5(米),.'.CF=CG+GF=25.5十4=29.5
米..29.5米>26米,.能实施有效救援,
类型2构造双直角三角形解决问题
(一)叠合式
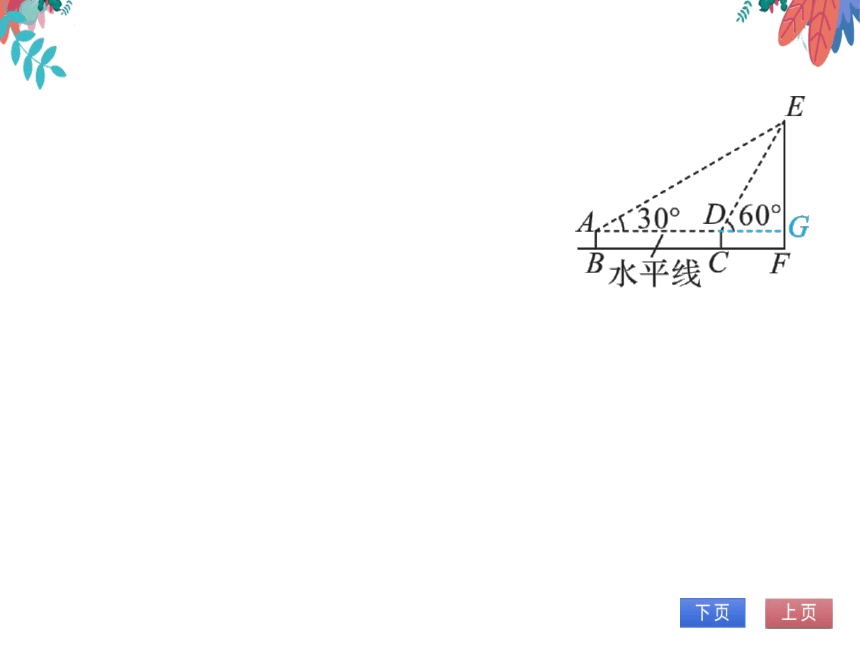
2.(2022·武汉)小红同学在数学活动课中测
量旗杆的高度,如图,已知测角仪的高度为
1.58米,她在A点观测旗杆顶端E的仰角
为30°,接着朝旗杆方向前进20米到达C
处,在D点观测旗杆顶端E的仰角为60°,
求旗杆EF的高度.(结果保留小数点后一
位)(参考数据:√3≈1.732)
解:过点D作DG⊥EF于点G,设EG
=x米,由题意可知:∠EAG=30°,
∠EDG=60,AD=20米,GF=1.584:130.60G
B水平线
F
米.在Kt△AEG中,tan∠EAG=AG'
EG
'.AG=√3x米.在Rt△DEG中,tan∠EDG=
E
DG,..DG=
3x-=20解得:x≈I7.3.EF5
x≈18.9(米).答:旗杆EF的高度约为18.9米.
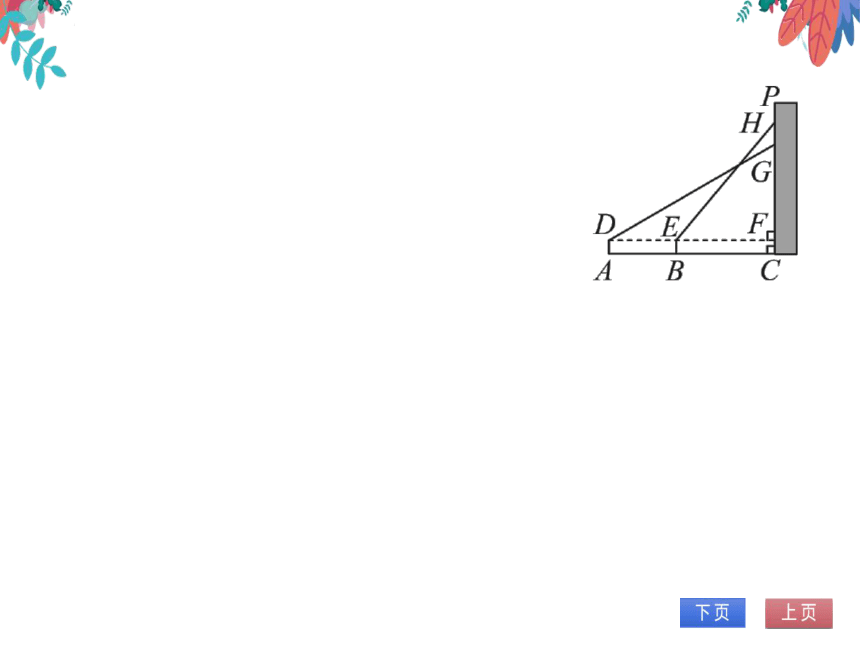
3.(2023·平顶山模拟)如图所示,为了知道
楼房CP外墙上一广告屏的高度GH是多
少,某数学活动小组利用测角仪和米尺等
工具进行如下操作:在A处测得GDF=
30°,在B处测得∠HEF=50°,点A、B、C
共线,AC⊥CP于点C,DF⊥CP于点F,
AB为20米,BC=30米,测角仪的高度
专题训练(十一) 解直角三角形的基本策略
第二十八章 锐角三角函数
必
●
类型1构造单一直角三角形解决问题
1.(2023·吉林模拟)消防车是救援火灾的主
要装备,图①是一辆登高云梯消防车的实
物图,图②是其工作示意图,起重臂AC
(20米≤AC≤30米)是可伸缩的,且起重
臂AC可绕点A在一定范围内上下转动张
角∠CAE(90°≤∠CAE≤150°),转动点A
距离地面的高度AE为4米.
(1)当起重臂AC的长度为24米,张角
∠CAE=120°时,登高云梯消防车最高点C
距离地面的高度CF的长为
16米.
(2)某日一栋大楼突发火灾,着火点距离地
面的高度为26米,该消防车在这栋楼
下能否实施有效救援?请说明理由.
(参考数据:√3≈1.7)(提示:当起重臂
AC伸到最长且张角∠CAE最大时,云
梯顶端C可以达到最大高度)
A
G
B E
①
②
解:(2)当起重臂最长,转动张角最大时,
即:AC=30米,∠CAE=150°,。∠CAG=
60°,.CG=AC·sin60°=30X
=15/3
2
≈25.5(米),.'.CF=CG+GF=25.5十4=29.5
米..29.5米>26米,.能实施有效救援,
类型2构造双直角三角形解决问题
(一)叠合式
2.(2022·武汉)小红同学在数学活动课中测
量旗杆的高度,如图,已知测角仪的高度为
1.58米,她在A点观测旗杆顶端E的仰角
为30°,接着朝旗杆方向前进20米到达C
处,在D点观测旗杆顶端E的仰角为60°,
求旗杆EF的高度.(结果保留小数点后一
位)(参考数据:√3≈1.732)
解:过点D作DG⊥EF于点G,设EG
=x米,由题意可知:∠EAG=30°,
∠EDG=60,AD=20米,GF=1.584:130.60G
B水平线
F
米.在Kt△AEG中,tan∠EAG=AG'
EG
'.AG=√3x米.在Rt△DEG中,tan∠EDG=
E
DG,..DG=
3x-=20解得:x≈I7.3.EF5
x≈18.9(米).答:旗杆EF的高度约为18.9米.
3.(2023·平顶山模拟)如图所示,为了知道
楼房CP外墙上一广告屏的高度GH是多
少,某数学活动小组利用测角仪和米尺等
工具进行如下操作:在A处测得GDF=
30°,在B处测得∠HEF=50°,点A、B、C
共线,AC⊥CP于点C,DF⊥CP于点F,
AB为20米,BC=30米,测角仪的高度
