【同步精讲-习题课件】第27章《相似》27.2.1 第1课时 平行线分线段成比例-人教版数学九下
文档属性
| 名称 | 【同步精讲-习题课件】第27章《相似》27.2.1 第1课时 平行线分线段成比例-人教版数学九下 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:50 | ||
图片预览






文档简介
(共21张PPT)
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
第二十七章 相似
必
●
知识要点全练
夯实基础
知识点1
相似三角形
1.若△ABC△DEF,AB=3,DE=5,则
△ABC与△DEF的相似比为
(A)
A.3:5
B.2:5
C.3:8
D.1:4
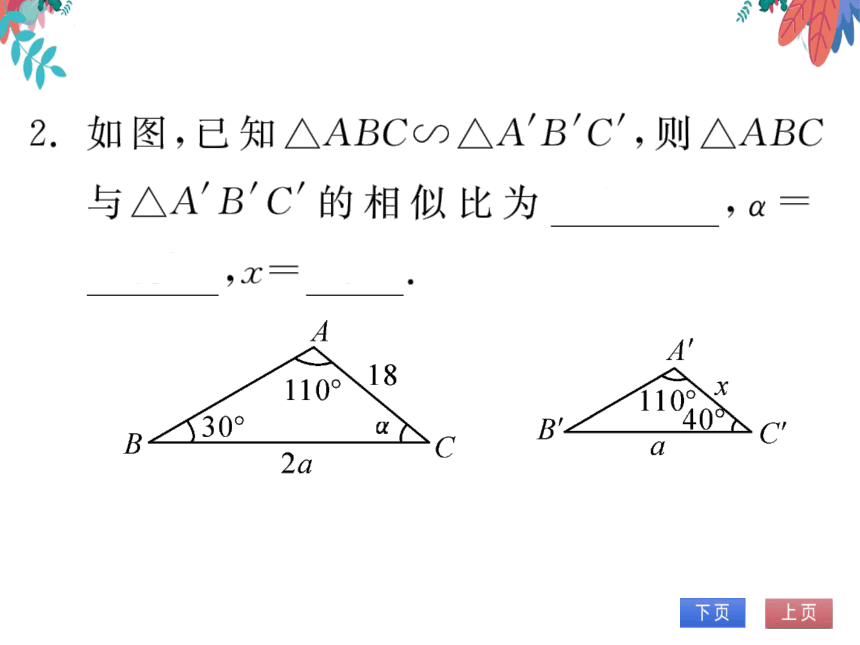
2.如图,已知∧ABC∽个A'B'C,则个ABC
与△AB'C'的相似比为
2:1
40°
A
110°
18
B
130°
B'∠
C
2a
知识点2
平行线分线段成比例
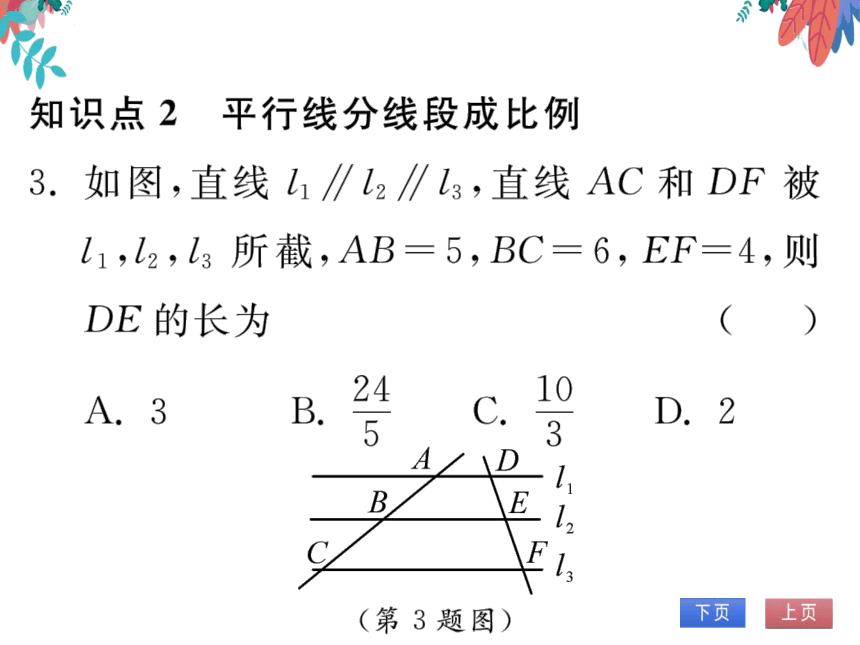
3.如图,直线U1∥l2∥13,直线AC和DF被
L1,l2,L3所截,AB=5,BC=6,EF=4,则
DE的长为
(C)
24
10
A.3
B.
C,
D.2
5
3
A∠1D-
B
E
F
(第3题图)
4.如图,点D、E、F分别是△ABC的边AB、
AC、BC上的点,若DE∥BC,EF∥AB,则
下列比例式一定成立的是
(A)
EF
FC
AD
A.
DE
AD
B.
BF
DB
BC
BF
EF
EF
DE
C.
BC
D.
AD
AB
BC
E
B
F
C
(第4题图)
5.如图,AB∥CDEF,AF与BE相交于点
G,且AG=2,GD=1,DF=5,BE=9.6,则
BC的长为
3.6
B
G
C
7E
F
(第5题图)
知识点3:
相似三角形判定预备定理
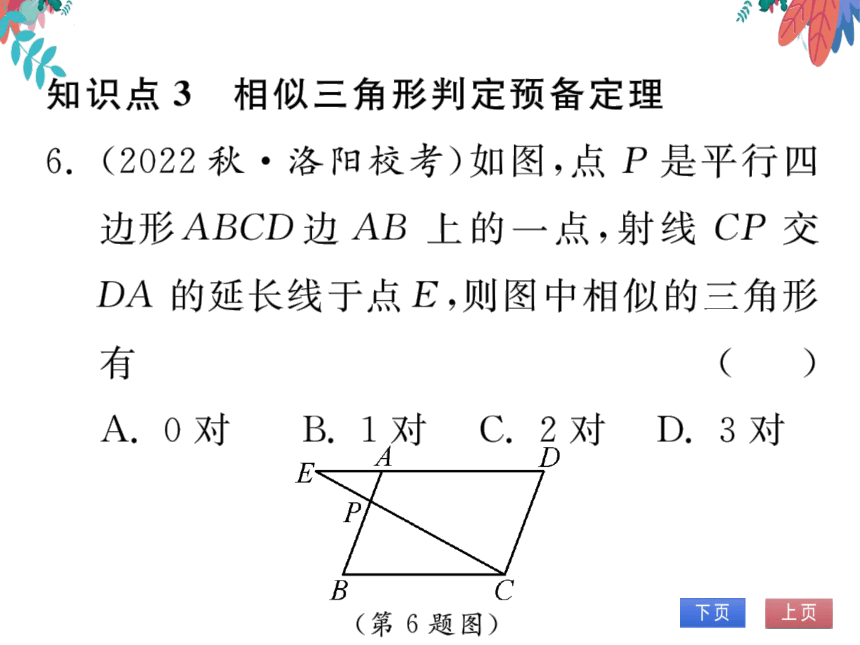
6.(2022秋·洛阳校考)如图,点P是平行四
边形ABCD边AB上的一点,射线CP交
DA的延长线于点E,则图中相似的三角形
有
D
A.0对
B.1对
C.2对
D.3对
A
E
D
P
B
C
(第6题图)
7.(2023春·龙岩期末)如图,在正方形
ABCD中,点E为CD边的中点,连接AE,
对角线BD交AE于点F,已知EF=1,则
线段AE的长度为3·
A
D
E
B
C
(第7题图)
8.(2023春·十堰期末)如图,在△ABC中,
EF∥CD,DE∥BC.
(1)求证:AF:FD=AD:DB;
(2)若AB=15,AD:BD=2:1,求DF
的长.
1)证明:EF/CD,
FD
E
,E方BC,
AE
AE
BD
EC
B
。
AF
AD
FD
BD
(2)AD:BD=2:1,BD=AD,AD+
IAD=15,:AD=10,AF:FD=AD:
DB,..AF:FD=2:1,..AF=2DF,.AF+
DF=10,.2DF+DF=10,.DF=
10
3。
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
第二十七章 相似
必
●
知识要点全练
夯实基础
知识点1
相似三角形
1.若△ABC△DEF,AB=3,DE=5,则
△ABC与△DEF的相似比为
(A)
A.3:5
B.2:5
C.3:8
D.1:4
2.如图,已知∧ABC∽个A'B'C,则个ABC
与△AB'C'的相似比为
2:1
40°
A
110°
18
B
130°
B'∠
C
2a
知识点2
平行线分线段成比例
3.如图,直线U1∥l2∥13,直线AC和DF被
L1,l2,L3所截,AB=5,BC=6,EF=4,则
DE的长为
(C)
24
10
A.3
B.
C,
D.2
5
3
A∠1D-
B
E
F
(第3题图)
4.如图,点D、E、F分别是△ABC的边AB、
AC、BC上的点,若DE∥BC,EF∥AB,则
下列比例式一定成立的是
(A)
EF
FC
AD
A.
DE
AD
B.
BF
DB
BC
BF
EF
EF
DE
C.
BC
D.
AD
AB
BC
E
B
F
C
(第4题图)
5.如图,AB∥CDEF,AF与BE相交于点
G,且AG=2,GD=1,DF=5,BE=9.6,则
BC的长为
3.6
B
G
C
7E
F
(第5题图)
知识点3:
相似三角形判定预备定理
6.(2022秋·洛阳校考)如图,点P是平行四
边形ABCD边AB上的一点,射线CP交
DA的延长线于点E,则图中相似的三角形
有
D
A.0对
B.1对
C.2对
D.3对
A
E
D
P
B
C
(第6题图)
7.(2023春·龙岩期末)如图,在正方形
ABCD中,点E为CD边的中点,连接AE,
对角线BD交AE于点F,已知EF=1,则
线段AE的长度为3·
A
D
E
B
C
(第7题图)
8.(2023春·十堰期末)如图,在△ABC中,
EF∥CD,DE∥BC.
(1)求证:AF:FD=AD:DB;
(2)若AB=15,AD:BD=2:1,求DF
的长.
1)证明:EF/CD,
FD
E
,E方BC,
AE
AE
BD
EC
B
。
AF
AD
FD
BD
(2)AD:BD=2:1,BD=AD,AD+
IAD=15,:AD=10,AF:FD=AD:
DB,..AF:FD=2:1,..AF=2DF,.AF+
DF=10,.2DF+DF=10,.DF=
10
3。
