【同步精讲-习题课件】第17章《勾股定理》本章重难点突破-人教版数学八下
文档属性
| 名称 | 【同步精讲-习题课件】第17章《勾股定理》本章重难点突破-人教版数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:50 | ||
图片预览






文档简介
(共30张PPT)
本章重难点突破
第十七章 勾股定理
必
●
考点1勾股定理及其应用
1.(2022秋·南关区期末)如图,在高为3米,
斜坡长为5米的楼梯台阶上铺地毯,则地
毯的长度至少要
(C)
A.5米
B.6米
C.7米
D.8米
B
5
3
m
m
A
C
(第1题图)
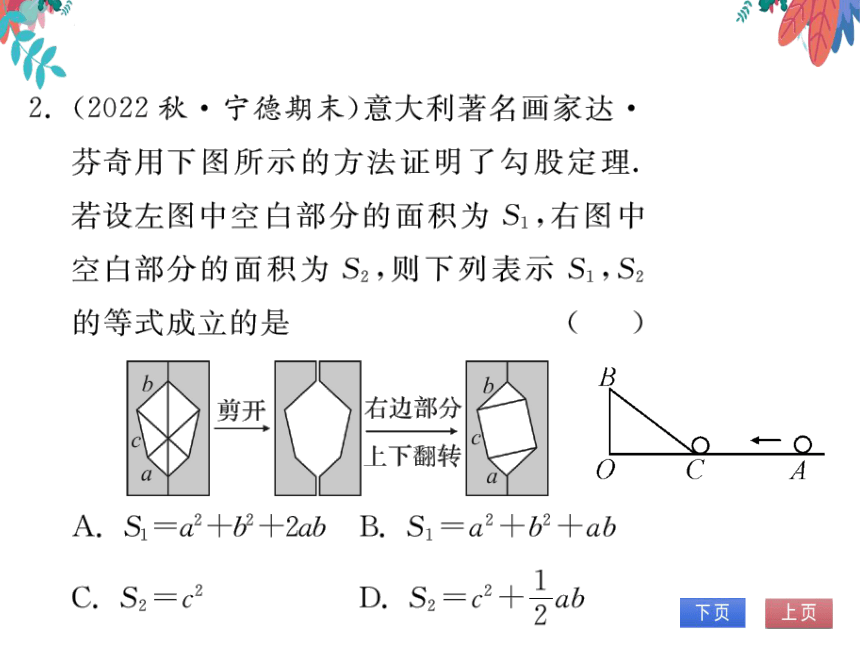
2.(2022秋·宁德期末)意大利著名画家达·
芬奇用下图所示的方法证明了勾股定理.
若设左图中空白部分的面积为S1,右图中
空白部分的面积为S2,则下列表示S1,S2
的等式成立的是
(B)
剪开
右边部分
上下翻转
a
A.S=a216212ab
B.S1=a2+b2十ab
C.S2=c2
D.S:-+gal
B
一
○
0
C
A
(第2题图)
3.(2021·福建)把两个同
E
样大小的含45°角的三角
尺按如图所示的方式放
B
置,其中一个三角尺的锐角顶点与另一个的
直角顶点重合于点A,且另三个锐角顶点B,
C,D在同一直线上.若AB=√2,则CD
=
√/3-1
■■■■■■■■
■
■
■
■
■
◆
◆
:
■
■
■
:
B
(第3题图)
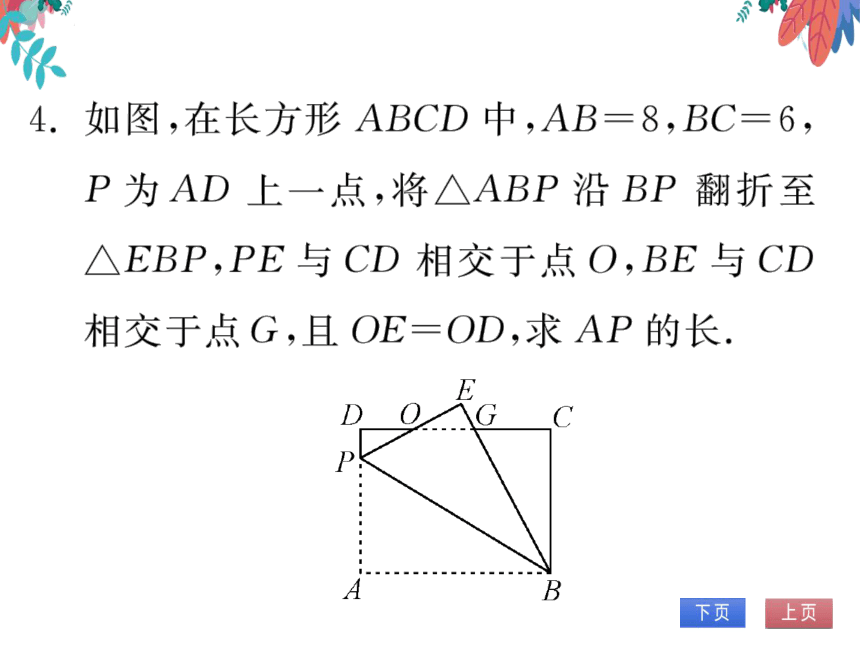
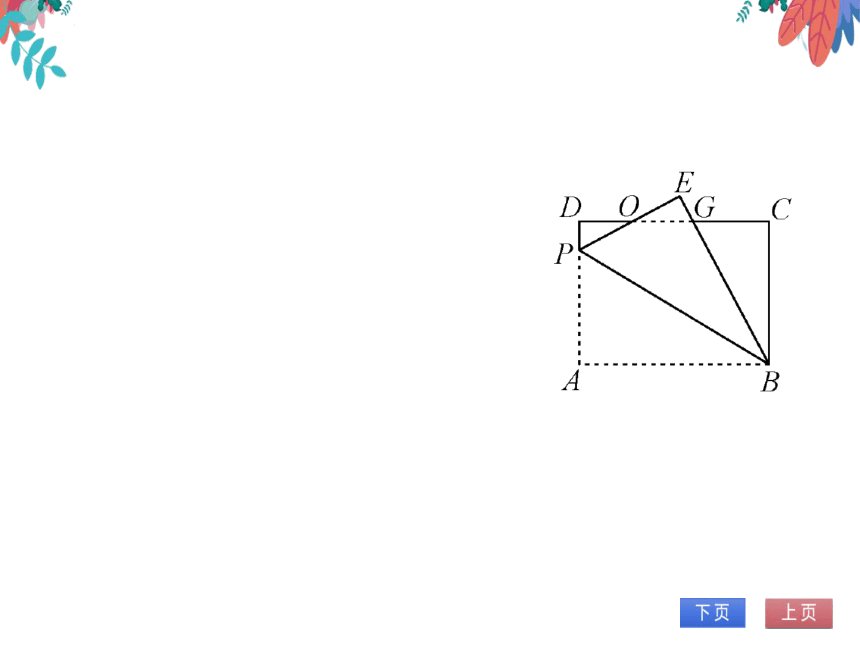
4.如图,在长方形ABCD中,AB=8,BC=6,
P为AD上一点,将△ABP沿BP翻折至
△EBP,PE与CD相交于点O,BE与CD
相交于点G,且OE=OD,求AP的长.
解:。四边形ABCD是长方形,
。∠D=∠A=∠C=90°,
C
AD=BC=6,CD=AB=8.
由折叠的性质可知EP=
AP,BE=AB=8,∠E=∠A
B
=90°,.∠E=∠D.
∠D=∠E,
在人ODP和△OEG中,OD=∠OE,
/DOP=∠EOG,
.'。∧ODP≌△OEG.。'.OP=OG,PD=GE.
。DO十OG=PO十OE..。DG=EP.
设AP=EP=DG=x,则
GB=PD=AD一
AP=6一K,。'.CG=DC一DG=8一K,BG=
BE一GE=8一(6一x)=2十x.
在Rt△CGD中,由勾股定理,得BC2十CG2
=BG2,即62十(8一x)2=(x十2)2,解得x=
4.8,。°.AP=4.8.
考点2勾股定理的逆定理及其应用
5.如图,点A的坐标为(一1,2),点B的坐标
为(2,1),有一点C在x轴上移动,则点C
到A,B两点的距离之和的最小值为(A)
A.32
B.4
C.3
D.4/2
本章重难点突破
第十七章 勾股定理
必
●
考点1勾股定理及其应用
1.(2022秋·南关区期末)如图,在高为3米,
斜坡长为5米的楼梯台阶上铺地毯,则地
毯的长度至少要
(C)
A.5米
B.6米
C.7米
D.8米
B
5
3
m
m
A
C
(第1题图)
2.(2022秋·宁德期末)意大利著名画家达·
芬奇用下图所示的方法证明了勾股定理.
若设左图中空白部分的面积为S1,右图中
空白部分的面积为S2,则下列表示S1,S2
的等式成立的是
(B)
剪开
右边部分
上下翻转
a
A.S=a216212ab
B.S1=a2+b2十ab
C.S2=c2
D.S:-+gal
B
一
○
0
C
A
(第2题图)
3.(2021·福建)把两个同
E
样大小的含45°角的三角
尺按如图所示的方式放
B
置,其中一个三角尺的锐角顶点与另一个的
直角顶点重合于点A,且另三个锐角顶点B,
C,D在同一直线上.若AB=√2,则CD
=
√/3-1
■■■■■■■■
■
■
■
■
■
◆
◆
:
■
■
■
:
B
(第3题图)
4.如图,在长方形ABCD中,AB=8,BC=6,
P为AD上一点,将△ABP沿BP翻折至
△EBP,PE与CD相交于点O,BE与CD
相交于点G,且OE=OD,求AP的长.
解:。四边形ABCD是长方形,
。∠D=∠A=∠C=90°,
C
AD=BC=6,CD=AB=8.
由折叠的性质可知EP=
AP,BE=AB=8,∠E=∠A
B
=90°,.∠E=∠D.
∠D=∠E,
在人ODP和△OEG中,OD=∠OE,
/DOP=∠EOG,
.'。∧ODP≌△OEG.。'.OP=OG,PD=GE.
。DO十OG=PO十OE..。DG=EP.
设AP=EP=DG=x,则
GB=PD=AD一
AP=6一K,。'.CG=DC一DG=8一K,BG=
BE一GE=8一(6一x)=2十x.
在Rt△CGD中,由勾股定理,得BC2十CG2
=BG2,即62十(8一x)2=(x十2)2,解得x=
4.8,。°.AP=4.8.
考点2勾股定理的逆定理及其应用
5.如图,点A的坐标为(一1,2),点B的坐标
为(2,1),有一点C在x轴上移动,则点C
到A,B两点的距离之和的最小值为(A)
A.32
B.4
C.3
D.4/2
