【同步精讲-习题课件】第18章《平行四边形》专题训练(四) 判定正方形两捷径-人教版数学八下
文档属性
| 名称 | 【同步精讲-习题课件】第18章《平行四边形》专题训练(四) 判定正方形两捷径-人教版数学八下 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:56 | ||
图片预览



文档简介
(共11张PPT)
专题训练(四) 判定正方形两捷径
第十八章 平行四边形
必
●
类型1从矩形角度出发
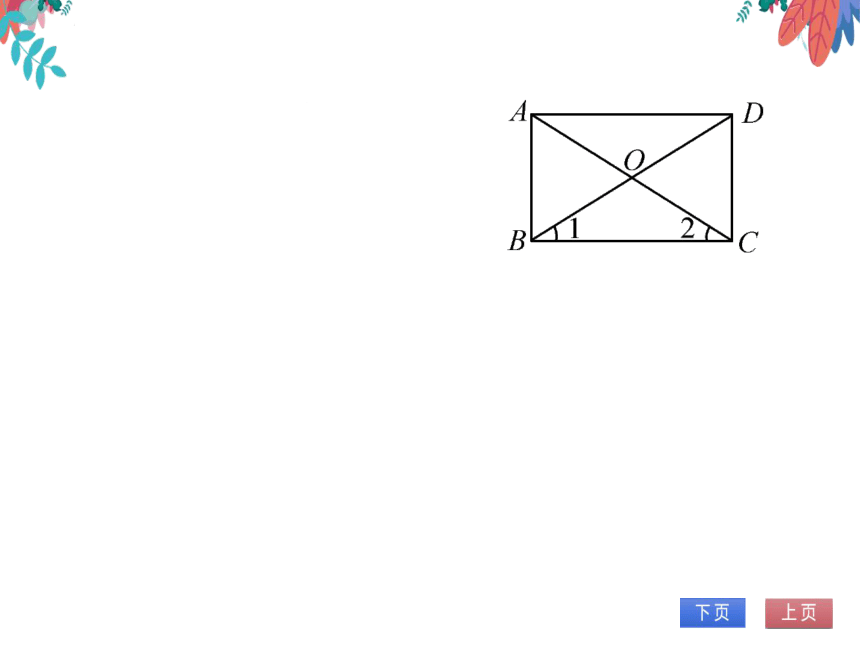
1.(2021·湖南邵阳)如图,在 ABCD中,对
角线AC,BD相交于点O,∠1=∠2.
(1)求证:四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD成为正
方形,并证明.
(1)证明:,·四边形ABCD
A
是平行四边形,
B
。'.BD=2OB,AC=2OC.
.∠1=∠2,.OB=OC.
。。BD=AC
又,四边形ABCD是平行四边形,
.四边形ABCD是矩形.
(2)解:添加AD=BC(答案不唯一),证明
如下:
.四边形ABCD是矩形,且AD=BC,
。矩形ABCD是正方形.
类型2从菱形角度出发
2.(2021·青岛)如图,在□ABCD中,O是
CD的中点,连接AO并延长,交BC的延
长线于点E.
(1)求证:AOD≌△EOC;
(2)连接AC,DE,当∠B=/AEB=45°
时,四边形ACED是正方形,请说明
理由.
(1)证明:O是CD的中点,
A
..OD=OC.
。·四边形ABCD是平行四边形,。AD
B
C
E
∥BC.
./ADO=∠OCE.
在△AOD和人EOC中,
∠ADO=∠OCE.
OD=OC,
..△AOD≌△EOC(ASA).
、/AOD=∠EOC,
(2)当∠B=∠AEB=45°时,四边形ACED为正方形,理由
如下:,△AOD≌△EOC,
.OA=OE,OC=OD,·'。四边形ACED是平行四边形.,。
AD=CE.,四边形ABCD是平行四边形,。AD=BC..
BC=CE..∠D=∠AEB=45°,.∠BAE=90°..在Rt
人ABE中,BC=CE,..AC=CE..四边形ACED是菱形.
,∠B=∠AEB,.AB=AE.又。BC=CE,.AC⊥BE.。
∠ACE=0°.又.四边形ACED是菱形,·'.四边形ACED
是正方形.
3.如图,AD是△ABC的角平分线,线段AD
的垂直平分线分别交AB和AC于点E,F,
连接DE,DF.
(1)试判断四边形AEDF的形状,并证明
你的结论;
(2)当△ABC满足什么条件时,四边形
AEDF是正方形?请说明理由.
解:(1)四边形AEDF是菱形.
证明:。°AD平分∠BAC,
E
'.∠BAD=∠CAD.
又。EF垂直平分AD,
B
.∠AOE=/AOF=90°.
又.AO=AO,
,。∧AOE2∧AOF.
专题训练(四) 判定正方形两捷径
第十八章 平行四边形
必
●
类型1从矩形角度出发
1.(2021·湖南邵阳)如图,在 ABCD中,对
角线AC,BD相交于点O,∠1=∠2.
(1)求证:四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD成为正
方形,并证明.
(1)证明:,·四边形ABCD
A
是平行四边形,
B
。'.BD=2OB,AC=2OC.
.∠1=∠2,.OB=OC.
。。BD=AC
又,四边形ABCD是平行四边形,
.四边形ABCD是矩形.
(2)解:添加AD=BC(答案不唯一),证明
如下:
.四边形ABCD是矩形,且AD=BC,
。矩形ABCD是正方形.
类型2从菱形角度出发
2.(2021·青岛)如图,在□ABCD中,O是
CD的中点,连接AO并延长,交BC的延
长线于点E.
(1)求证:AOD≌△EOC;
(2)连接AC,DE,当∠B=/AEB=45°
时,四边形ACED是正方形,请说明
理由.
(1)证明:O是CD的中点,
A
..OD=OC.
。·四边形ABCD是平行四边形,。AD
B
C
E
∥BC.
./ADO=∠OCE.
在△AOD和人EOC中,
∠ADO=∠OCE.
OD=OC,
..△AOD≌△EOC(ASA).
、/AOD=∠EOC,
(2)当∠B=∠AEB=45°时,四边形ACED为正方形,理由
如下:,△AOD≌△EOC,
.OA=OE,OC=OD,·'。四边形ACED是平行四边形.,。
AD=CE.,四边形ABCD是平行四边形,。AD=BC..
BC=CE..∠D=∠AEB=45°,.∠BAE=90°..在Rt
人ABE中,BC=CE,..AC=CE..四边形ACED是菱形.
,∠B=∠AEB,.AB=AE.又。BC=CE,.AC⊥BE.。
∠ACE=0°.又.四边形ACED是菱形,·'.四边形ACED
是正方形.
3.如图,AD是△ABC的角平分线,线段AD
的垂直平分线分别交AB和AC于点E,F,
连接DE,DF.
(1)试判断四边形AEDF的形状,并证明
你的结论;
(2)当△ABC满足什么条件时,四边形
AEDF是正方形?请说明理由.
解:(1)四边形AEDF是菱形.
证明:。°AD平分∠BAC,
E
'.∠BAD=∠CAD.
又。EF垂直平分AD,
B
.∠AOE=/AOF=90°.
又.AO=AO,
,。∧AOE2∧AOF.
