【同步精讲-习题课件】第18章《平行四边形》专题训练(五) 四边形中的数学思想-人教版数学八下
文档属性
| 名称 | 【同步精讲-习题课件】第18章《平行四边形》专题训练(五) 四边形中的数学思想-人教版数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:56 | ||
图片预览



文档简介
(共11张PPT)
专题训练(五) 四边形中的数学思想
第十八章 平行四边形
必
●
类型1数形结合思想
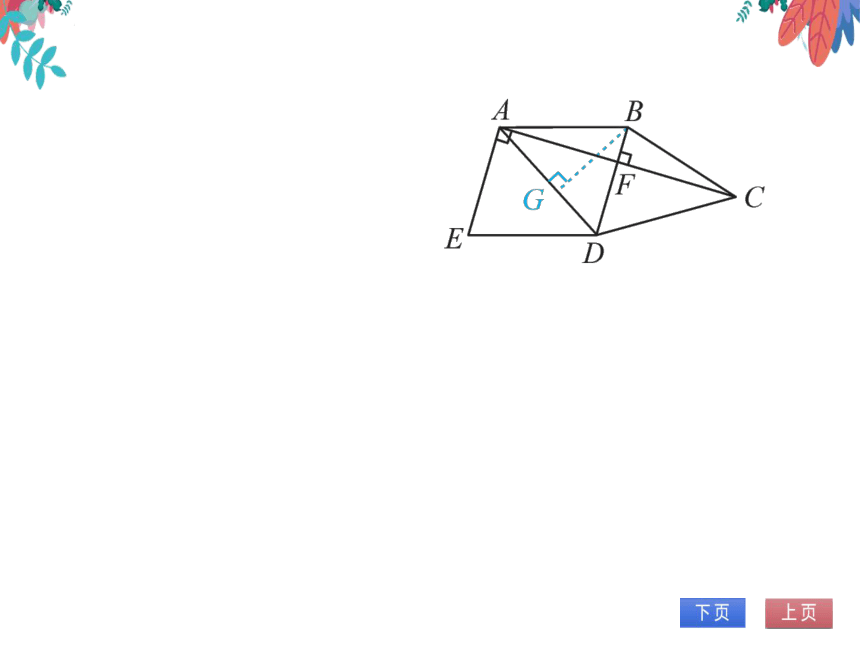
1.如图,在四边形ABCD中,BD垂直平分
AC,垂足为F,E为四边形ABCD外一点,
且∠ADE=∠BAD,AEAC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,
求AC的长.
(1)证明:.BD⊥AC,AE⊥AC,
A
B
.。∠CFD=∠CAE=90°...AE
C
∥BD.∠ADE=∠BAD,·E
AD∥ED.
·'.四边形ABDE是平行四边形.
(2)解:过点D作BG⊥AD于点G.,DA平分∠DDE,
.∠ADE=∠ADB.又.·∠ADE=∠BAD,.∠ADB=
∠BAD.BA=BD=5.叉:BGLAD,AG=号AD=3.
G=5-3F=4.:Sm=号·BD·A=方·AD
·BG,.AF=4D·BG=6X4_24
BD
5
5
,BD垂直平分AC,.AC=2AF=2X
2448
5
类型2方程思想
2.如图,M,N分别是正方形ABCD的边BC,
CD上的点,已知∠MAN=30°,AM=AN,
△AMN的面积为1.
(1)求∠BAM的度数;
(2)求正方形ABCD的边长.
解:(1)先证△ABM2△ADN(HL),
D
得∠BAM=30°.
E
(2)过点M作ME⊥AN于点E,则AN=
N
AM-2ME.
B
M
C
设MWE=x,则AN=AM=2x,
"S2=)AN·ME=1,2·2x·x=1,
AM=2.BM=号AM=2X2=1.
.AD=/22一12=√3.
类型3分类讨论思想
3.若正方形ABCD的边长为4,E是BC边上
一点,BE=3,M为线段AE上一点,射线
BM交正方形的一边于点F,且BF=AE,
求BM的长.
F D
B
E
C
B
①
2
解:(1)当点F在AD边上时,如图①,连接
EF。。·四边形ABCD是正方形,。AD升
BC,∠BAF=∠ABE=0°.又。°BF=AE,
BA=AB,。。Rt△BAF≌Rt人ABE.,。AF=
BE=3.又。°AF∥DE,。四边形ABEF是
平行四边形。又,BF=AE,。□ABEF是
矩形,BM=
BF.在Rt△BAF中,BF=
2
√AF2+AB2=VW32+4=5,".BM=
2
(2)当点F在CD边上时,如图②,同理可
证得Rt△ABE≌Rt人BCF,。'。∠1=∠2..”
∠1十∠3=90°,.。∠2十∠3=90°,BM
AE,即BM是Rt△ABE斜边AE上的高.
专题训练(五) 四边形中的数学思想
第十八章 平行四边形
必
●
类型1数形结合思想
1.如图,在四边形ABCD中,BD垂直平分
AC,垂足为F,E为四边形ABCD外一点,
且∠ADE=∠BAD,AEAC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,
求AC的长.
(1)证明:.BD⊥AC,AE⊥AC,
A
B
.。∠CFD=∠CAE=90°...AE
C
∥BD.∠ADE=∠BAD,·E
AD∥ED.
·'.四边形ABDE是平行四边形.
(2)解:过点D作BG⊥AD于点G.,DA平分∠DDE,
.∠ADE=∠ADB.又.·∠ADE=∠BAD,.∠ADB=
∠BAD.BA=BD=5.叉:BGLAD,AG=号AD=3.
G=5-3F=4.:Sm=号·BD·A=方·AD
·BG,.AF=4D·BG=6X4_24
BD
5
5
,BD垂直平分AC,.AC=2AF=2X
2448
5
类型2方程思想
2.如图,M,N分别是正方形ABCD的边BC,
CD上的点,已知∠MAN=30°,AM=AN,
△AMN的面积为1.
(1)求∠BAM的度数;
(2)求正方形ABCD的边长.
解:(1)先证△ABM2△ADN(HL),
D
得∠BAM=30°.
E
(2)过点M作ME⊥AN于点E,则AN=
N
AM-2ME.
B
M
C
设MWE=x,则AN=AM=2x,
"S2=)AN·ME=1,2·2x·x=1,
AM=2.BM=号AM=2X2=1.
.AD=/22一12=√3.
类型3分类讨论思想
3.若正方形ABCD的边长为4,E是BC边上
一点,BE=3,M为线段AE上一点,射线
BM交正方形的一边于点F,且BF=AE,
求BM的长.
F D
B
E
C
B
①
2
解:(1)当点F在AD边上时,如图①,连接
EF。。·四边形ABCD是正方形,。AD升
BC,∠BAF=∠ABE=0°.又。°BF=AE,
BA=AB,。。Rt△BAF≌Rt人ABE.,。AF=
BE=3.又。°AF∥DE,。四边形ABEF是
平行四边形。又,BF=AE,。□ABEF是
矩形,BM=
BF.在Rt△BAF中,BF=
2
√AF2+AB2=VW32+4=5,".BM=
2
(2)当点F在CD边上时,如图②,同理可
证得Rt△ABE≌Rt人BCF,。'。∠1=∠2..”
∠1十∠3=90°,.。∠2十∠3=90°,BM
AE,即BM是Rt△ABE斜边AE上的高.
