【同步精讲-习题课件】第18章《平行四边形》本章重难点突破-人教版数学八下
文档属性
| 名称 | 【同步精讲-习题课件】第18章《平行四边形》本章重难点突破-人教版数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:56 | ||
图片预览






文档简介
(共32张PPT)
本章重难点突破
第十八章 平行四边形
必
●
考点1平行四边形的性质与判定
1.(2023春·庐江县期中)在□ABCD中,已
知∠A+∠C=160°,则∠A=
(C)
A.40°
B.60°
C.80°
D.
1009
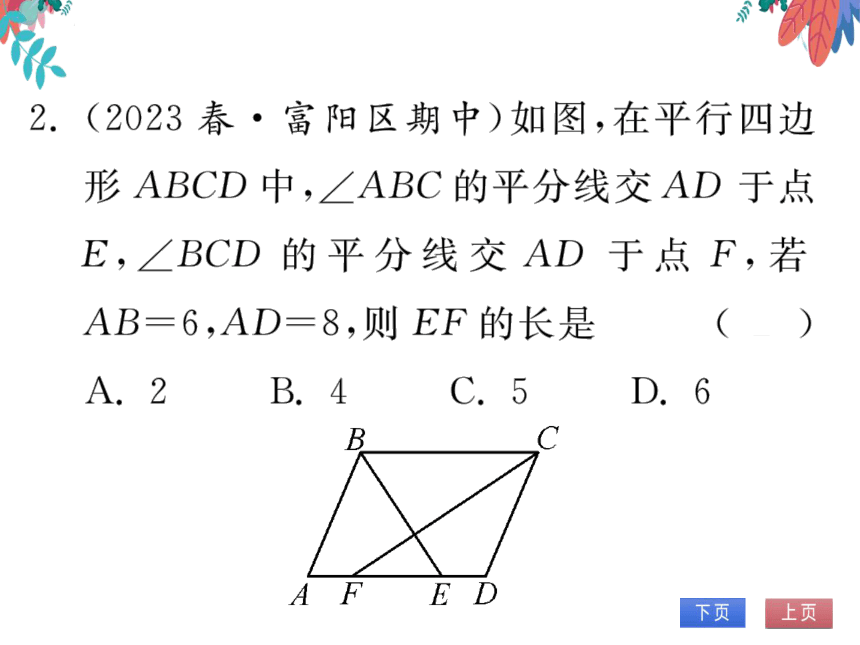
2.(2023春·富阳区期中)如图,在平行四边
形ABCD中,∠ABC的平分线交AD于点
E,∠BCD的平分线交AD于点F,若
AB=6,AD=8,则EF的长是
(B)
A.2
B.4
C.5
D.6
B
C
A
F
ED
(第2题图)
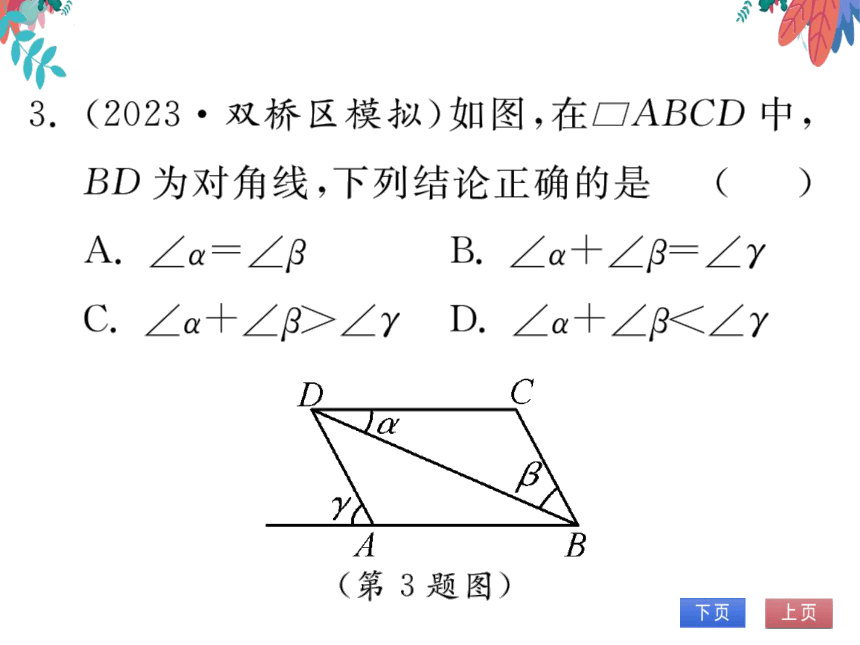
3.(2023·双桥区模拟)如图,在 ABCD中,
BD为对角线,下列结论正确的是
B
A.∠a=∠3
B.∠a+∠B=∠Y
C.∠+∠B>∠Y
D.∠a+∠B∠Y
D
C
a
G
Y公
A
B
(第3题图)
4.(2023春·张北县期中)在平行四边形
ABCD中,AB=5cm,已知对角线AC、BD
相交于O,且AC=6cm,BD=8cm,则平
行四边形ABCD的面积为
B
A.15 cm2 B.24 cm2 C.48 cm2 D.20 cm2
5.(2021·天津)如图,
口ABCD的顶点C在等
边△BEF的边BF上,点A
E
B
E在AB的延长线上,G为DE的中点,连
接CG.若AD=3,AB=CF=2,则CG的
长为1.5
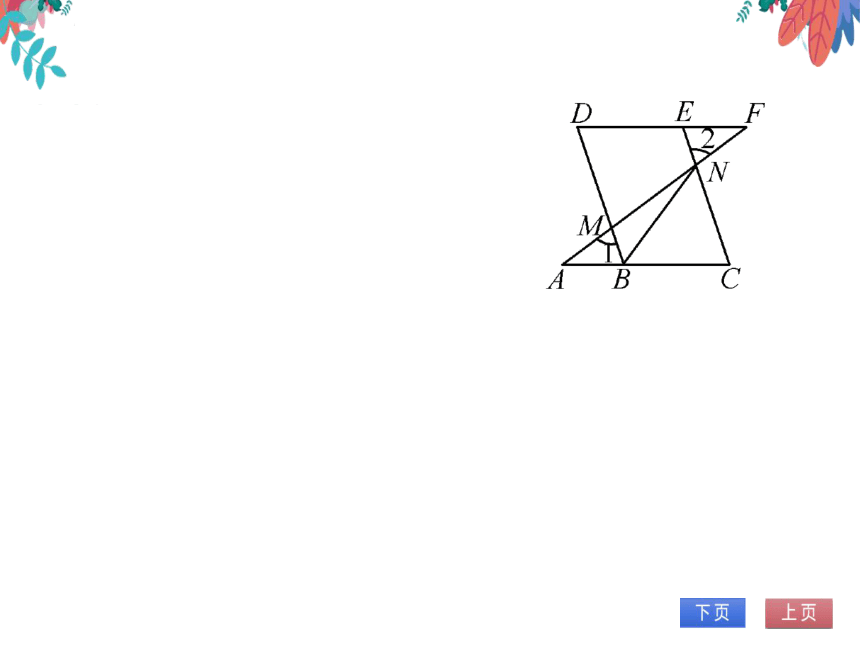
6.如图,点B,E分别在AC,DF上,AF分别交
BD,CE于点M,V,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=3,连接BN,若BN平分
∠DBC,求CN的长.
(1)证明:,∠A=∠F,
D
E
2
.DE∥BC.
N
.∠1=∠2,且∠1
A
B
∠DMF,
.∠DMF=∠2.
。'.DB∥EC.
'.四边形BCED是平行四边形.
(2)解:,BN平分∠DBC,
。∠DBN=∠CBN.
,EC∥DB,.∠CND=∠DBN.
.∠CNB=∠CBN.
.'.CN=BC=DE=3.
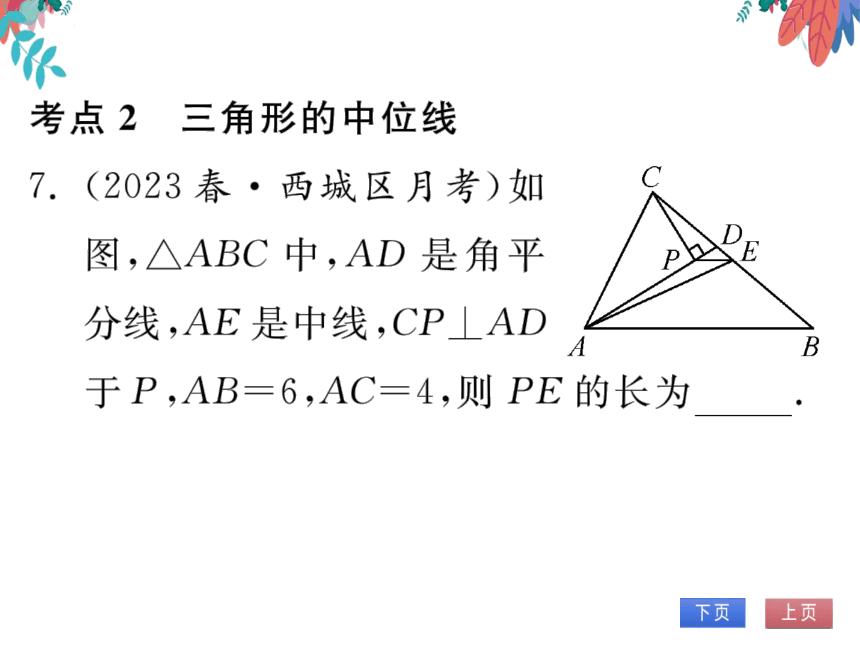
考点2三角形的中位线
7.(2023春·西城区月考)如
图,△ABC中,AD是角平
分线,AE是中线,CP AD
B
于P,AB=6,AC=4,则PE的长为1
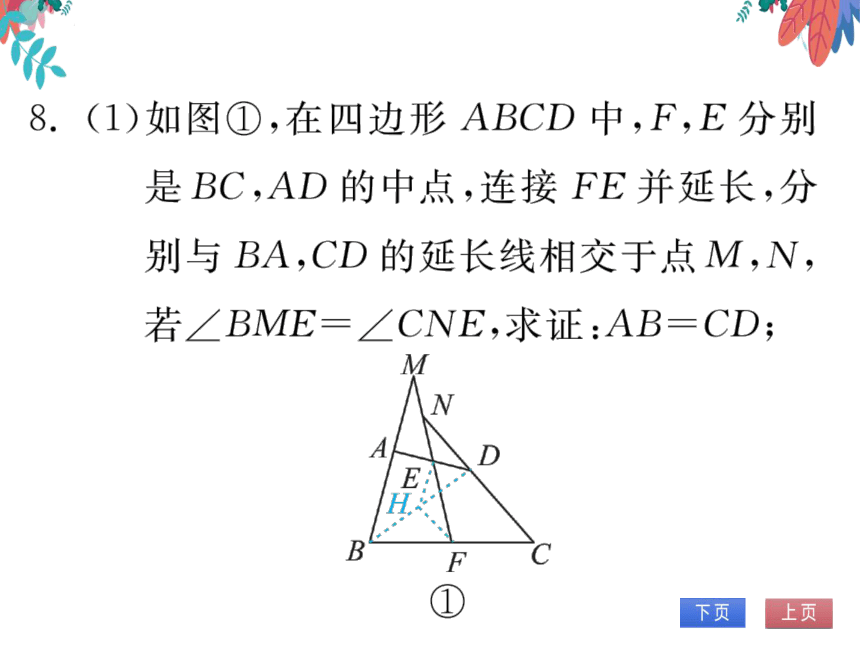
8.(1)如图①,在四边形ABCD中,F,E分别
是BC,AD的中点,连接FE并延长,分
别与BA,CD的延长线相交于点M,V,
若∠BME=∠CNE,求证:AB=CD;
本章重难点突破
第十八章 平行四边形
必
●
考点1平行四边形的性质与判定
1.(2023春·庐江县期中)在□ABCD中,已
知∠A+∠C=160°,则∠A=
(C)
A.40°
B.60°
C.80°
D.
1009
2.(2023春·富阳区期中)如图,在平行四边
形ABCD中,∠ABC的平分线交AD于点
E,∠BCD的平分线交AD于点F,若
AB=6,AD=8,则EF的长是
(B)
A.2
B.4
C.5
D.6
B
C
A
F
ED
(第2题图)
3.(2023·双桥区模拟)如图,在 ABCD中,
BD为对角线,下列结论正确的是
B
A.∠a=∠3
B.∠a+∠B=∠Y
C.∠+∠B>∠Y
D.∠a+∠B∠Y
D
C
a
G
Y公
A
B
(第3题图)
4.(2023春·张北县期中)在平行四边形
ABCD中,AB=5cm,已知对角线AC、BD
相交于O,且AC=6cm,BD=8cm,则平
行四边形ABCD的面积为
B
A.15 cm2 B.24 cm2 C.48 cm2 D.20 cm2
5.(2021·天津)如图,
口ABCD的顶点C在等
边△BEF的边BF上,点A
E
B
E在AB的延长线上,G为DE的中点,连
接CG.若AD=3,AB=CF=2,则CG的
长为1.5
6.如图,点B,E分别在AC,DF上,AF分别交
BD,CE于点M,V,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=3,连接BN,若BN平分
∠DBC,求CN的长.
(1)证明:,∠A=∠F,
D
E
2
.DE∥BC.
N
.∠1=∠2,且∠1
A
B
∠DMF,
.∠DMF=∠2.
。'.DB∥EC.
'.四边形BCED是平行四边形.
(2)解:,BN平分∠DBC,
。∠DBN=∠CBN.
,EC∥DB,.∠CND=∠DBN.
.∠CNB=∠CBN.
.'.CN=BC=DE=3.
考点2三角形的中位线
7.(2023春·西城区月考)如
图,△ABC中,AD是角平
分线,AE是中线,CP AD
B
于P,AB=6,AC=4,则PE的长为1
8.(1)如图①,在四边形ABCD中,F,E分别
是BC,AD的中点,连接FE并延长,分
别与BA,CD的延长线相交于点M,V,
若∠BME=∠CNE,求证:AB=CD;
