【同步精讲-习题课件】第19章《一次函数》专题训练(六) 一次函数中的面积问题-人教版数学八下
文档属性
| 名称 | 【同步精讲-习题课件】第19章《一次函数》专题训练(六) 一次函数中的面积问题-人教版数学八下 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:56 | ||
图片预览



文档简介
(共9张PPT)
专题训练(六) 一次函数中的面积问题
第十九章 一次函数
必
●
类型1由一次函数的图象求面积
1.(2021·四川自贡)如图,
Rt人ABC放在平面直角坐标
系内,其中∠CAB=90°,BC=
B
5,点A,B的坐标分别为(1,
0),(4,0),将△ABC沿x轴向右平移,当
点C落在直线y=2x一6上时,线段BC扫
过的面积为
16
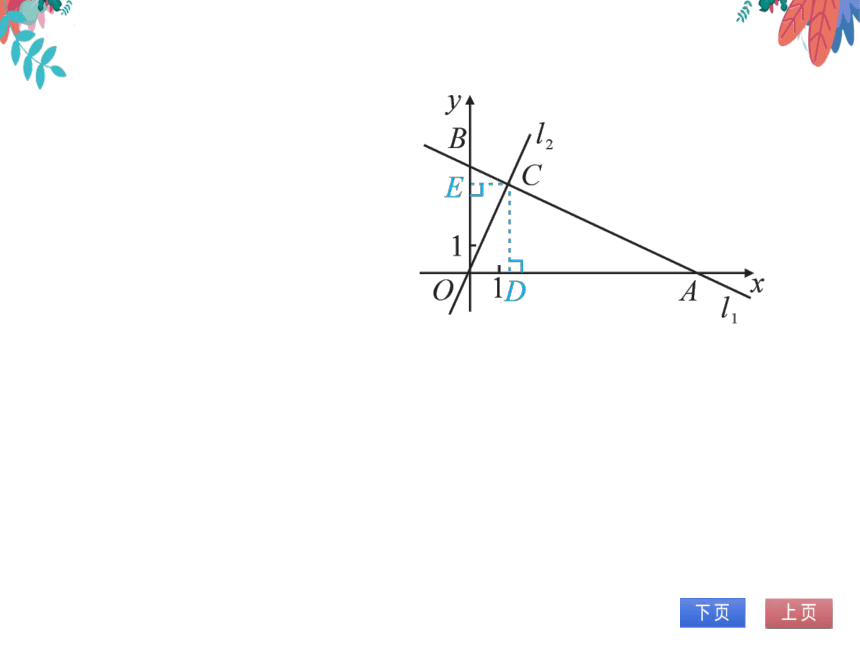
2.(2021·河北)如图,在直角坐标系xOy中,
中次数v=)x十5的图象 分别凸
x,y轴交于A,B两点,正比例函数的图象
l2与11交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△Aoc-SAoC的值;
(3)一次函数y=kx+1的图象为l3,且L1,l2,
3不能围成三角形,直接写出k的值.
解:(1)把C(m,4)的坐标代
y↑
B
入=-号+5中,得
E
2m+5=4,m=2,
1
A I
.C(2,4).设l2的解析式为y=ax,则
2a=4,.a=2,.l2的解析式为y=2x.
(2)如图,过点C作CDOA于点D,CE⊥OB于点E,则CD=
4,CE=2.对于y=-2十5,令x=0,则y=5,令y=0,
1
则x=10,
..A(10,0),B(0,5)...OA=10,OB=5.
:Sm-Sm-号×10X4-2×5X2=20-5=15.
(3)当1经过点C(2,4)时,k=
2
当,平行时,k=一7;当,6平行时,k=2.综上,k
的值为-或或2.
类型2由面积关系确定一次函数解析式
3.如图,A,B分别是x轴上位于原点两侧的
点,点P(2,)在第一象限,直线PA交y
轴于点C(0,2),直线PB交y轴于点D,
△AOP的面积为6.
(1)求△COP的面积;
(2)求点A的坐标及力的值;
(3)若△BOP与△DOP的面积相等,求直
线BD的解析式.
解:(1)过点P作PE⊥y轴于点E.
Sm=·0·P=X2X
2=2.
Bx
(2),S△A0c=S△40r一S△or=6-
2=4,Sm=号0100=4.
OAX2=4..OA=4..A(一4,0).
设直线AP的解析式为y=kx十b,
把A(一4,0),C(0,2)坐标代入上式,得
-4k+b=0,.k=2
y=x+2.
b=2,
b=2.
把P(2,p)的坐标代入=+2中,得p=×2+2=3.
(3)设直线DD的解析式为y=mx+n.(m≠0)
.S△0r=S△or且P(2,3),∴.3OB=2OD,
0B=子00=子B(3,0),
把B(子,0),P(2,3)坐标代入y=mx+n中,得
号mm十n=0,.m=
2m+n=3,
n=6.
直线BD的解析式为y=一
2r+6.
专题训练(六) 一次函数中的面积问题
第十九章 一次函数
必
●
类型1由一次函数的图象求面积
1.(2021·四川自贡)如图,
Rt人ABC放在平面直角坐标
系内,其中∠CAB=90°,BC=
B
5,点A,B的坐标分别为(1,
0),(4,0),将△ABC沿x轴向右平移,当
点C落在直线y=2x一6上时,线段BC扫
过的面积为
16
2.(2021·河北)如图,在直角坐标系xOy中,
中次数v=)x十5的图象 分别凸
x,y轴交于A,B两点,正比例函数的图象
l2与11交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△Aoc-SAoC的值;
(3)一次函数y=kx+1的图象为l3,且L1,l2,
3不能围成三角形,直接写出k的值.
解:(1)把C(m,4)的坐标代
y↑
B
入=-号+5中,得
E
2m+5=4,m=2,
1
A I
.C(2,4).设l2的解析式为y=ax,则
2a=4,.a=2,.l2的解析式为y=2x.
(2)如图,过点C作CDOA于点D,CE⊥OB于点E,则CD=
4,CE=2.对于y=-2十5,令x=0,则y=5,令y=0,
1
则x=10,
..A(10,0),B(0,5)...OA=10,OB=5.
:Sm-Sm-号×10X4-2×5X2=20-5=15.
(3)当1经过点C(2,4)时,k=
2
当,平行时,k=一7;当,6平行时,k=2.综上,k
的值为-或或2.
类型2由面积关系确定一次函数解析式
3.如图,A,B分别是x轴上位于原点两侧的
点,点P(2,)在第一象限,直线PA交y
轴于点C(0,2),直线PB交y轴于点D,
△AOP的面积为6.
(1)求△COP的面积;
(2)求点A的坐标及力的值;
(3)若△BOP与△DOP的面积相等,求直
线BD的解析式.
解:(1)过点P作PE⊥y轴于点E.
Sm=·0·P=X2X
2=2.
Bx
(2),S△A0c=S△40r一S△or=6-
2=4,Sm=号0100=4.
OAX2=4..OA=4..A(一4,0).
设直线AP的解析式为y=kx十b,
把A(一4,0),C(0,2)坐标代入上式,得
-4k+b=0,.k=2
y=x+2.
b=2,
b=2.
把P(2,p)的坐标代入=+2中,得p=×2+2=3.
(3)设直线DD的解析式为y=mx+n.(m≠0)
.S△0r=S△or且P(2,3),∴.3OB=2OD,
0B=子00=子B(3,0),
把B(子,0),P(2,3)坐标代入y=mx+n中,得
号mm十n=0,.m=
2m+n=3,
n=6.
直线BD的解析式为y=一
2r+6.
